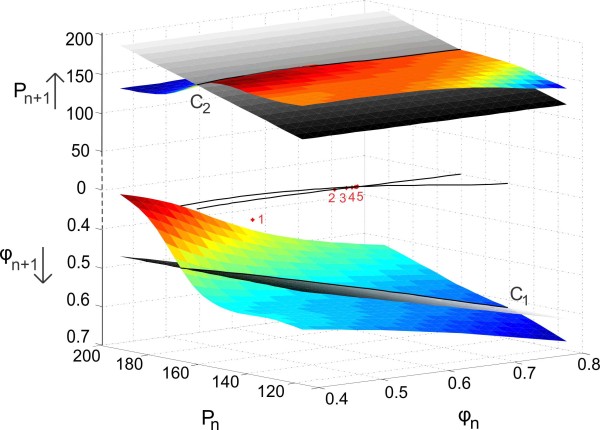
Fig. 8.

Fixed points of 2D (3.24) map when $P_0=Q_0$ obtained by solving (3.26). The surfaces for the evolution of period and intrinsic phase of the 2D map with synaptic preferred periods $P_{\mathrm{A}}=150$, $P_{\mathrm{B}}=190$ are drawn above and below the $z=0$ plane denoted by the axes $z_1=P_{n+1}$ and $z_2={\varphi }_{n+1}$, respectively. The equality $P_n=P_{n+1}$ is satisfied when the surface $z_1={\Pi }_2(x,y)$ (colored surface on top) and the plane $z_1=y$ (gray-scaled plane on top) intersect. Similarly, the equality ${\varphi }_n={\varphi }_{n+1}$ is satisfied when the surface $z_2={\Pi }_1(x,y)$ (colored surface on bottom) intersects the plane $z_2=x$ (gray-scaled plane on bottom). These intersections yield the two black curves above and below the $z=0$ plane. The fixed point of the map lies on the intersection of the two fixed point curves. The projections of these curves on the $z=0$ plane are shown together with the iterates (red dots) approaching the fixed point at their intersection in the order enumerated in the figure