Ultrametric distribution of culture vectors in an extended Axelrod model of cultural dissemination

Abstract

The Axelrod model of cultural diffusion is an apparently simple model that is capable of complex behaviour. A recent work used a real-world dataset of opinions as initial conditions, demonstrating the effects of the ultrametric distribution of empirical opinion vectors in promoting cultural diversity in the model. Here we quantify the degree of ultrametricity of the initial culture vectors and investigate the effect of varying degrees of ultrametricity on the absorbing state of both a simple and extended model. Unlike the simple model, ultrametricity alone is not sufficient to sustain long-term diversity in the extended Axelrod model; rather, the initial conditions must also have sufficiently large variance in intervector distances. Further, we find that a scheme for evolving synthetic opinion vectors from cultural “prototypes” shows the same behaviour as real opinion data in maintaining cultural diversity in the extended model; whereas neutral evolution of cultural vectors does not.

An enduring question of cultural dynamics is the convergence or divergence of cultures over time. Does increasing global communication and intercultural contact reduce cultural diversity? Axelrod's simple, but powerful model of cultural diffusion¹ has been used to explore this question². Some recent extensions explored the effects of introducing stochastic³,⁴,⁵,⁶, complex network⁷, and thermodynamic quantities⁸ into the system. Others have investigated more specifically social mechanisms that facilitate or hamper the persistence of cultural diversity, including the use of social (that is, interactions between more than two actors) rather than dyadic influence⁹, social network reshaping controlled by intolerance¹⁰, the effect of mass media modelled as an external field¹¹,¹²,¹³,¹⁴, as well as others (e.g. Klemm et al. [3], Centola et al. [15], Greig [16], Klemm et al. [17], Pfau et al. [18]).

Much less explored are the effects of characteristics of the cultural space itself on cultural dynamics. This relative neglect has persisted despite Axelrod's initial investigation, which as discussed below showed that a characteristic of the cultural space is critical for cultural diversity. Valori et al.¹⁹ addressed this gap by pointing to the critical role of the ultrametricity²⁰ of cultural space. This article is based on the insights of that work. We confirm that ultrametricity is important, but show that, in the extended Axelrod model of Pfau et al. [18], it is not sufficient to sustain long term diversity.

Axelrod conceptualised cultural space largely in line with the contemporary empirical research on cultural diversity, where cultures are typically represented as configurations or profiles of responses to a variety of cultural issues (for example Kashima [21], Triandis [22]). The cultural issues vary a great deal depending on the domain of cultural activities; people's attitudes towards science and technology (for example Valori et al. [19], which we also use here), personal values or moral domains such as freedom, loyalty, and purity (for example Schwartz [23], Graham et al. [24]). A range of responses can exist for each issue. Assuming that there are F dimensions and q possible responses, the cultural space is defined by the q^F points. In Axelrod's model, each agent is assumed to possess a profile of cultural traits represented as a point in this space.

The Axelrod model is essentially a cellular automaton. At each step, a random agent and one of its neighbours is chosen. With probability proportional to their cultural similarity, they interact. Cultural similarity between two agents can be measured by the number of traits they have in common (that is, the number of corresponding elements in each agent's vector which have the same value). An interaction consists of a randomly chosen trait in one agent being changed to become identical to that trait of the other. This is repeated until convergence, at which point any two neighbouring agents have either identical or completely distinct culture vectors. Axelrod's investigation showed that q is critical for the persistence of cultural diversity – while keeping F constant, the greater is q, the more likely cultural diversity persists. Axelrod called this factor the scope of cultural possibilities. The greater the number of cultural profiles possible in the cultural space, the more likely that cultural diversity will persist.

Although subsequent research has shown that the effect of q on cultural diversity is robust under different conditions (e.g. Pfau et al. [18]), there is a limitation in this line of work. The initial culture vectors are typically set by randomly selecting culture vectors from a uniform distribution over the cultural space. Going beyond this limitation, Valori et al.¹⁹ used empirical responses to a large scale European public opinion survey as initial culture vectors. They used the bounded confidence variant of the Axelrod model, in which a threshold θ is defined, such that agents can only interact when their cultural similarity is greater than or equal to θ. If θ = 0 then this is equivalent to the model without bounded confidence. The rationale is that agents need a minimum level of “common ground” to interact at all. The threshold θ can be used to define the culture graph. In this graph any two agents are adjacent when their cultural similarity is greater than or equal to θ. Each connected component in the culture graph is then a set of agents that can possibly interact with each other in the Axelrod model with bounded confidence threshold θ.

Based on their simulation results, Valori et al. argued that ultrametricity of the distribution of culture vectors is critical for the maintenance of cultural diversity. Specifically, they compared the absorbing state of the Axelrod model using as initial states (1) the real culture vectors based on opinion data, (2) random culture vectors, and (3) permuted culture vectors, which were generated by shuffling real data (each trait's values permuted among individuals so as to destroy correlations between responses by the same individual). First of all, they noted the clear differences between the ultrametric structure of the real data relative to the random and permuted data. This was done by inspection of the hierarchical clustering dendrogram, where they argued it was apparent “by eye” that the real data are “more ultrametric” than the shuffled or random data. They also reported that, for a given number of initial connected components in the culture graph, it is the real (ultrametric) culture vectors that lead to the greatest number of surviving cultures Valori et al. (SI Text) [19].

Intriguingly, however, they measured inter-opinion correlations and noted that real data also have greater variance in intervector distances than random or permuted data Valori et al. (SI Text) [19]. Variance in intervector distances is conceptually related to scope of cultural possibilities in Axelrod's original investigation. A greater variance implies that, when the mean of intervector distances is constant, culture vectors can differ in many traits, and therefore a greater diversity of cultures is possible. It follows that cultural diversity persisted in Valori et al.'s real culture vectors more than in the random or permuted ones potentially due to ultrametricity as well as greater variance in intervector distances.

In the present paper, we extend Valori et al.'s investigation in three respects. First, we show that the observed distribution of culture vectors is not only characterised by ultrametricity, but also by a large scope of cultural possibilities, and that ultrametricity differs from the latter – it is possible to vary ultrametricity while keeping scope of cultural possibilities relatively constant. Second, we show that a large scope of cultural possibilities is a precondition for ultrametric culture vectors to maintain long-term cultural diversity in an extended Axelrod model (the model described originally in Pfau et al. [18]). Only when the scope of cultural possibilities is sufficiently large, can ultrametric culture vectors sustain greater cultural diversity in the extended model. This is in contrast to the simple Axelrod model (as used in Valori et al. [19]), in which ultrametricity is sufficient. Finally, we propose a simple method called prototype evolution, which allows us to evolve a set of ultrametric culture vectors with a large scope of cultural possibilities. We show that the initial culture vectors simulated with this method can reproduce the pattern of cultural dynamics observed with the real culture vectors in the extended Axelrod model, suggesting a possibility that cultural representations can be construed in terms of prototypes and their variants. This fits with prominent social science prototype theories as discussed below.

Results

We investigate the effects of ultrametricity and variance in intervector distances on cultural diversity in two steps. First, we quantify the degree of ultrametricity and examine the properties of real culture vectors in two different data sets: Eurobarometer data that Valori et al. used, and General Social Survey data from the USA. We confirm Valori et al.'s observation that the distribution of real culture vectors is characterised by ultrametricity and large variance in intervector distances. Second, we describe the neutral evolution, prototype evolution, and trivial ultrametric methods, three methods by which ultrametrically distributed culture vectors can be simulated. The neutral evolution method enables us to vary ultrametricity while keeping the mean and variance of intervector distances relatively constant, whereas the prototype evolution method generates culture vectors that vary ultrametricity and variance in intervector distances at the same time, which mimic the pattern only observable in real culture vectors. The trivial ultrametric method allows us to vary ultrametricity and mean of intervector distances, while variance remains low. If ultrametricity is the critical factor for cultural diversity, the neutral evolution and trivial ultrametric methods should be able to reproduce the pattern of cultural dynamics observable with real data, whereas the prototype evolution method should reproduce the cultural dynamics based on the real culture vectors if the combination of ultrametricity and a large variance in intervector distances is necessary. Details of the schemes are given in the Methods section.

Table 1 shows the mean and standard deviation of inter-vector distances in Eurobarometer data (real, shuffled, random and simulated), as well as the degree of ultrametricity as measured by the cophenetic correlation coefficient and ultrametric triangle fraction (defined in Methods). As a second empirical data set for initial opinion vectors, we use the same approach as for the Eurobarometer data, applied to the General Social Survey (GSS) 1993 data²⁵. Table 2 shows the statistics for this data. The real opinion data is more ultrametric (higher cophenetic correlation coefficient) and has larger standard deviation of intervector distances than permuted or random data. It is notable that the cophenetic correlation coefficient largely accords with the intuitive notion, as visualised using dendrograms, that real data is more ultrametric than permuted or random data, as described in Valori et al. [19], while ultrametric triangle fraction does not. Indeed the ultrametric triangle fraction for random data is higher than for real data, and is in all cases small. For this reason, and the sensitivity of this direct, or “literal”, measurement of ultrametricity to even small perturbations in the data²⁶, that we will use the cophenetic correlation coefficient as our measurement of ultrametricity, and only include the values of the ultrametric triangle fraction for comparison. Details of the data sets and the measurement of ultrametricity are given in the Methods section.

Table 1. Statistics of inter-vector distances, and cophenetic correlation coefficients and ultrametric triangle fractions for Eurobarometer survey data (N = 600), with the split ballot question handled by merging versions so that F = 116.

description	mean intervector distance	sd of intervector distance	cophenetic corr. coeff.	ultrametric tri. frac.
Real	0.585	0.076	0.316	0.066
Permuted	0.585	0.041	0.344	0.095
Random	0.798	0.037	0.028	0.099
Simulated	0.909	0.030	0.093	0.128
Simulated permuted	0.909	0.027	0.034	0.137

Table 2. Statistics of inter-vector distances, and cophenetic correlation coefficients and ultrametric triangle fractions for GSS survey data (N = 600), merging split ballots so that F = 58.

description	mean intervector distance	sd of intervector distance	cophenetic corr. coeff.	ultrametric tri. frac.
Real	0.717	0.114	0.695	0.109
Permuted	0.717	0.057	0.296	0.134
Random	0.858	0.046	0.031	0.160
Simulated	0.889	0.051	0.123	0.160
Simulated permuted	0.889	0.041	0.028	0.178

We use two different versions of the Axelrod model. The first, which we will refer to as the simple Axelrod model, is similar to that used in Valori et al.¹⁹. The second, which we will refer to as the extended Axelrod model, is the model from Pfau et al.¹⁸. Details are given in the Methods section and Supplementary Information.

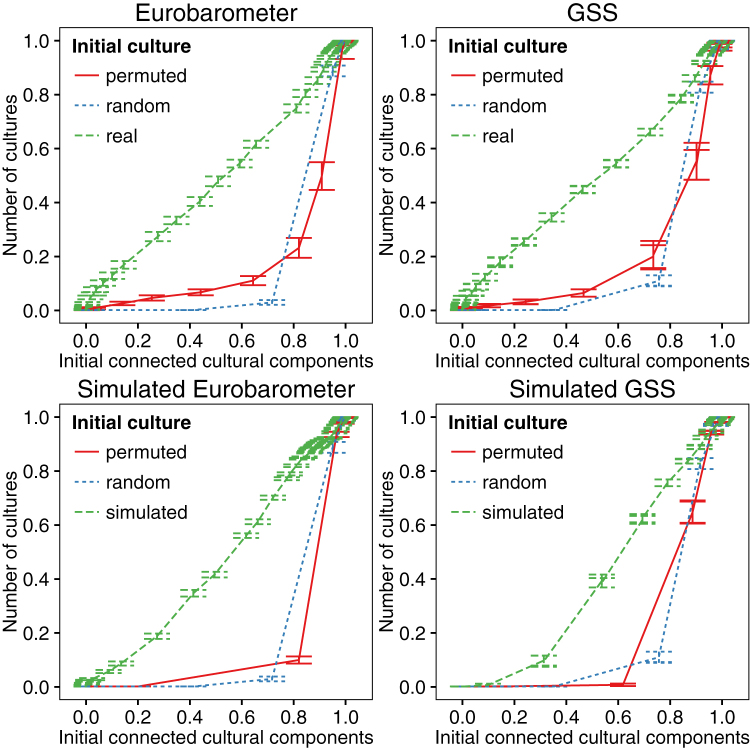
Fig. 1 shows results in the simple Axelrod model, reproducing the results described in Valori et al. (SI Text) [19] that the real data (for both Eurobarometer and GSS, as well as their simulated versions) has the largest number of cultures at the absorbing state for a given number of initially compatible agents. Fig. 2, for the extended Axelrod model, shows that, for a given number of initially compatible agents, real data again has the largest number of cultures at the absorbing state. Although the modified Axelrod model we use, incorporating social ties and geographical migration, with discrete values of cultural traits, is quite different from the simpler model used in Valori et al. [19], our result here is similar in this respect, although the effect is much smaller. We note that the real Eurobarometer data has a larger number of cultures at the absorbing state than the permuted and random data for a given number of initial connected cultural components, even though it has a smaller cophenetic correlation coefficient than the permuted data. It does, however, have a larger standard deviation of intervector distances (Table 1).

Figure 1. Number of cultures at the absorbing state (y axis) in the simple Axelrod model versus number of initial connected culture components (x axis) for Eurobarometer and GSS data (N = 600), both real and simulated using random values with the same covariance as the real data.

The value of θ is varied to obtain different numbers of initial connected components in the culture graphs along the x axis and the corresponding numbers of cultures (normalised to lie between 0 and 1 by dividing by N) at the absorbing state on the y axis.

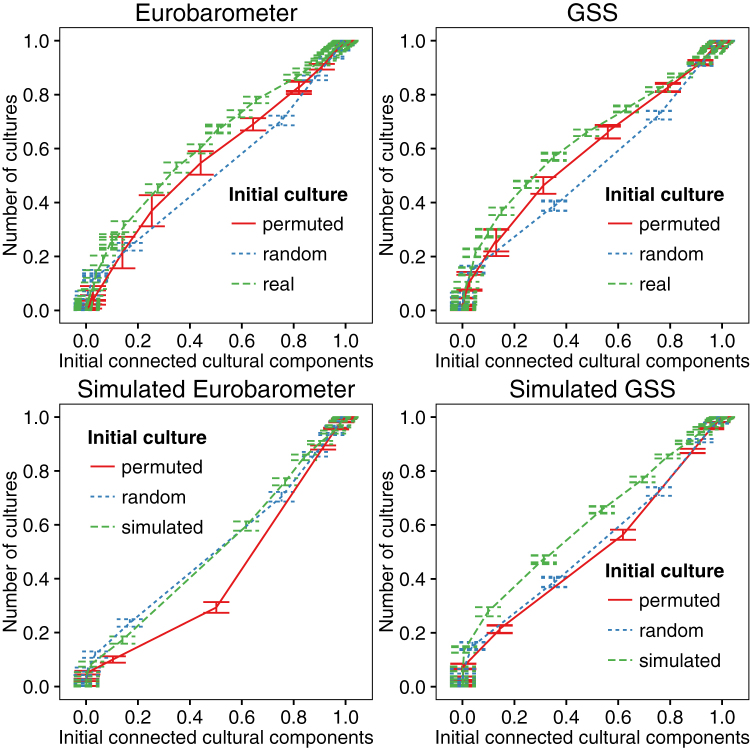
Figure 2. Number of cultures at the absorbing state (y axis) in the extended Axelrod model versus number of initial connected culture components (x axis) for Eurobarometer and GSS data (N = 600), both real and simulated using random values with the same covariance as the real data.

The value of θ is varied to obtain different numbers of initial connected components in the culture graphs along the x axis and the corresponding numbers of cultures (normalised to lie between 0 and 1 by dividing by N) at the absorbing state on the y axis.

Another point to note is that in the extended model (Fig. 2), the data points mostly occupy the upper, rather than the lower, triangle of the graph. This is an unexpected result if we consider the discussion in Valori et al. (SI Text) [19], that the diagonal on these graphs represents the “largest possible” number of cultures at the absorbing state, and that, further, results due to properties of the initial conditions are surprisingly robust to differences between various modifications of the dynamic rules of the Axelrod model. Our extended Axelrod model would appear to fit within the scenarios reduced to equivalence with the simple model in Valori et al. (SI Text) [19]; different interaction probabilities (as an increasing function of cultural similarity; mediated in our model by geographical migration and social link weight), and social networks co-evolving with opinions. However, as we will show later, curves on these graphs above the diagonal (occupying the upper triangle) are possible even in the simple Axelrod model.

Fig. 1 and Fig. 2 also show the results for the GSS data. As with the Eurobarometer data, real data has the largest number of cultures at the absorbing state for a given number of initially compatible agents. Hence this result is not specific to European data and is also robust to certain other differences in the data; the GSS data has a considerably smaller value of F (see Supplementary Information), and, unlike the Eurobarometer data which we have sampled so that there are (an equal number of) samples from each of the 12 European countries in the data, all the samples are from the same country.

The simulated data has the same covariance structure as the real data, but, as is evident from Table 1 and Table 2, a much lower cophenetic correlation coefficient. Like the real data, the simulated GSS data has a greater number of cultures at the absorbing state for a given number of initial connected components in the culture graph in both models, however this is not the case for the simulated Eurobarometer data in the extended Axelrod model (Fig. 2). Table 1 shows that the simulated Eurobarometer data, despite having a higher cophenetic correlation coefficient than its permuted form and random data, in fact has a smaller standard deviation of intervector distance than random data; this, rather than only the degree of ultrametricity (as measured by cophenetic correlation coefficient), may be causing these effects in the Eurobarometer data.

Investigating the effects of ultrametricity and intervector distance

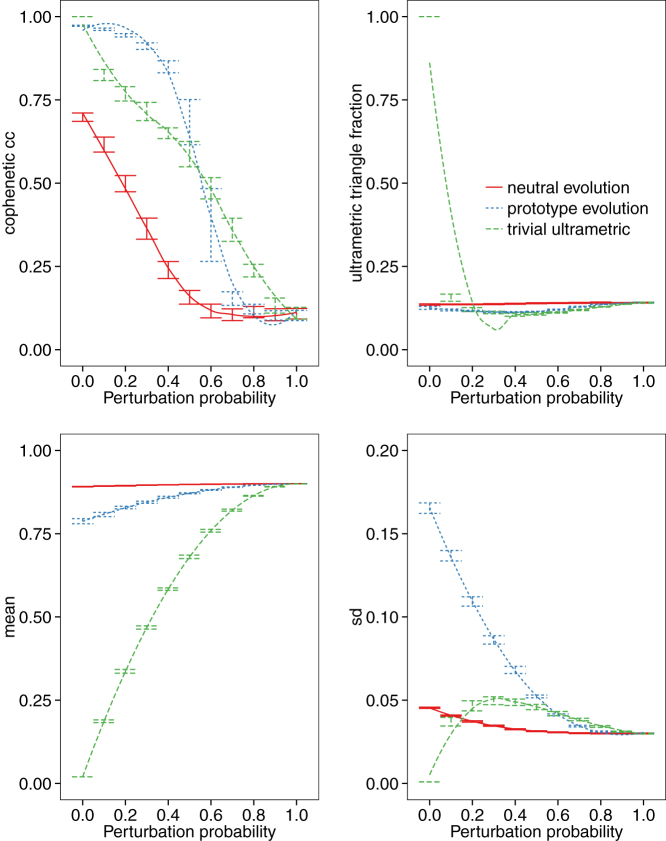
We investigate the effects of ultrametricity and intervector distance by using three different schemes to generate initial culture vectors. We can achieve this by first generating ultrametrically distributed initial culture vectors, and then reducing the degree of ultrametricity by randomly perturbing each element of each vector independently with a fixed probability p. As we will show below, different schemes produce varying degrees of ultrametricity and intervector distances, such that their effects can be examined separately. If p = 0 then the data is just the ultrametric data just created; if p = 1 then the data is uniform random data. Intermediate values give intermediate degrees of ultrametricity (as measured by cophenetic correlation coefficient) as shown in Fig. 3. Ultrametricity also increases with increasing dimension (F) and with increasing sparsity²⁰,²⁷, as shown in the Supplementary Information. Note that the ultrametric triangle fraction remains small and approximately constant (just like the real, perturbed, simulated and random data) for the neutral evolution and prototype evolution schemes. Only the trivial ultrametric scheme creates a larger value of ultrametric triangle fraction, and then only the value 1 when p = 0 (by construction); any perturbation at all immediately decreases it to a similar value to the other schemes and random data.

Figure 3. Ultrametricity, and mean and standard deviation of intervector distances, generated by the three schemes of generating initial culture vectors.

F = 100, q = 10, N = 125.

Fig. 3 also shows how statistics of the intervector distances vary with perturbation probability p in all three schemes. In prototype evolution, the standard deviation of intervector distance decreases with decreasing ultrametricity. In neutral evolution, the mean and standard deviation of the intervector distances remain approximately constant, and p affects mainly the degree of ultrametricity. Therefore, using this scheme we can use p as a proxy for the degree of the ultrametricity of the initial conditions, while with prototype evolution it also has significant effects on the mean, and, especially, variance, of intervector distances. In the trivial ultrametric scheme, the mean intervector distance starts just above zero and increases smoothly as ultrametricity decreases, while the standard deviation starts at zero and when perturbed at all increases to a still relatively small value where it then converges to the value for random data as ultrametricity decreases.

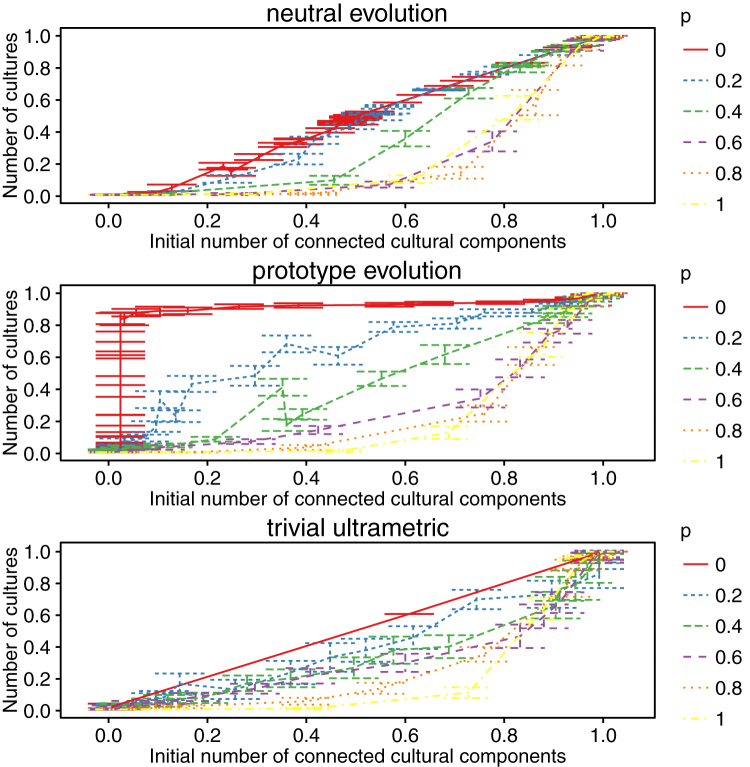
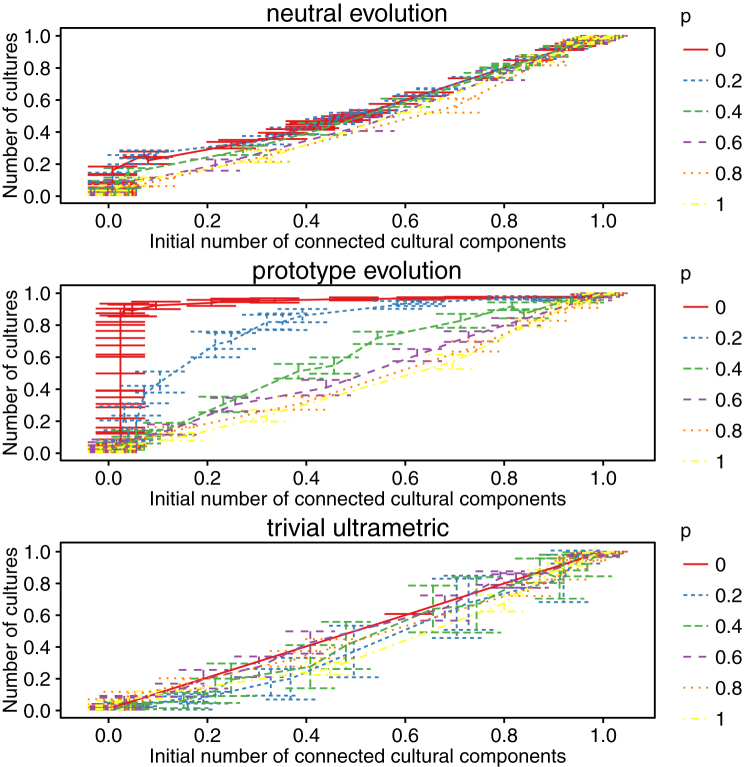
Fig. 4 shows, for all three schemes in the simple Axelrod model, the number of cultures at the absorbing state against the number of connected components in the initial culture graph. Both neutral evolution and the trivial ultrametric scheme show similar results to real data in the simple model; the most ultrametric data is approximately on the diagonal, with the curve further below the diagonal in the lower triangle as the degree of ultrametricity decreases. Surprisingly, however, prototype evolution shows the most ultrametric curve well above the diagonal in the upper triangle, and the curves for initial data with lower degrees of ultrametricity successively beneath it, with the p = 0.4 curve approximately on the diagonal. As we previously mentioned, this result may seem impossible if we believe that the largest possible number of cultures at the absorbing state is along the diagonal. However (as is evident from this result), given the right distribution of initial culture vectors, curves above the diagonal are indeed possible, even in the simple model. We show how this is possible by constructing the simplest case in the Supplementary Information.

Figure 4. Number of cultures at the absorbing state in the simple Axelrod model plotted against number of connected components in the culture graph of initial conditions for three different schemes to generate initial culture vectors for various initial perturbation probabilities p.

The value of θ is varied to obtain different numbers of initial connected components in the culture graphs along the x axis and the corresponding numbers of cultures at the absorbing state is shown on the y axis. F = 100, q = 10, N = 125.

Fig. 5 shows the results in the extended Axelrod model. These graphs show that, when using neutral evolution or the trivial ultrametric scheme to generate initial culture vectors, we do not see a larger number of cultures at the absorbing state for increasing ultrametricity. Only prototype evolution shows the curves in order of decreasingly ultrametric initial conditions, showing that the more ultrametric data has a larger number of cultures at the absorbing state for a given number of initially culturally compatible agents. It is particularly significant that neutral evolution does not have this property, since, as shown in Fig. 3, increasing the perturbation probability p in this scheme decreases ultrametricity as measured by the cophenetic correlation coefficient, but leaves the mean and standard deviation of the intervector distances approximately constant. However this alone is not enough to show that ultrametricity is not sufficient for a greater number of surviving cultures, since the maximum value of the cophenetic correlation coefficient is only approximately 0.72 for neutral evolution, while it is approximately 0.97 for prototype evolution (Fig. 3), which leaves open the possibility that it is the greater ultrametricity possible in prototype evolution that leads to the greater number of cultures. However, the results from the trivial ultrametric scheme confirm that ultrametricity is not sufficient for a greater number of cultures, as in this scheme the maximum cophenetic correlation coefficient is 1 at p = 0 by construction. In addition, neutral evolution with different parameters can show a higher cophenetic correlation coefficient, further confirming this result (see Supplementary Information).

Figure 5. Number of cultures at the absorbing state in the extended Axelrod model plotted against number of connected components in the culture graph of initial conditions for three different schemes to generate initial culture vectors for various initial perturbation probabilities p.

The value of θ is varied to obtain different numbers of initial connected components in the culture graphs along the x axis and the corresponding numbers of cultures at the absorbing state is shown on the y axis. F = 100, q = 10, N = 125.

Discussion

In Valori et al. [19], it is shown that an ultrametric distribution of culture vectors in the initial conditions of an Axelrod model preserves diversity at the absorbing state. We quantified the degree of ultrametricity of sets of empirical initial culture vectors from survey data, and also data generated in such a way as to have varying degrees of ultrametricity. Our results confirm those of Valori et al. [19] in the simple model, but show ultrametricity itself is not sufficient for this preservation of diversity in the extended Axelrod model; the initial vectors must also have sufficiently high scope of cultural possibilities, as for example measured by the variance in intervector distances (as used for example in the SI Text of Valori et al. [19]). An ultrametric distribution of the culture vectors (as measured by cophenetic correlation coefficient), does not necessarily imply a high variance of this distribution. Real data, however, does have both properties.

In the simple Axelrod model, ultrametricity alone is sufficient to show behaviour similar to empirical data. However the scheme for evolving synthetic initial opinion vectors based on “prototypes” shows even greater preservation of cultural diversity at the absorbing state; the empirical data and other two schemes for initial conditions do not result in the greatest possible number of cultures at the absorbing state. In the extended Axelrod model, only this prototype evolution scheme for generating initial culture vectors results in the same property that real data has, of simultaneously having large variance of intervector distances and being ultrametrically distributed, thereby preserving diversity at the absorbing state. This suggests that real culture vectors may arise with the distribution that they have as a result of evolution from, or clustering around, “prototype” culture vectors.

Methods

We use two variations of the Axelrod model, which we have referred to as the “simple” and “extended” Axelrod models. The simple Axelrod model is similar to that used in Valori et al.¹⁹. The differences from the original Axelrod model¹ are that, first, the bounded confidence threshold θ is introduced, and second, rather than only interacting with their immediate neighbours, an agent can interact with any other agent (the social network is a complete graph). The extended Axelrod model is the model of Pfua et al. [18], which extends the Axelrod model by co-evolving social networks and geographical mobility along with culture. We extend it to include bounded confidence. In the Pfau et al.¹⁸ model, there are N agents on an L² lattice, as in the original Axelrod model. However, agents can now move on the lattice (geographical mobility), and there is also a social network, with weighted undirected social links between agents. The probability of an interaction between two agents depends on their geographical and social proximity. In addition, interactions can be either successful or unsuccessful; the probability of an interaction being successful is proportional to the cultural similarity between the agents. A successful interaction results not only in a cultural trait becoming identical, but also an increase in the weight of the social link between the two agents. An unsuccessful interaction results in a decrease in the weight of a social tie, and also potential geographical migration on the lattice towards another social contact.

For both models, the results are means (with error bars giving one standard deviation) of running the model to the absorbing state 50 times with the same initial conditions. Further details are given in the Supplementary Information.

Ultrametricity and intervector distance in real culture vectors

In order to investigate the effect of ultrametricity, it is necessary to quantify ultrametricity. An ultrametric space²⁰ is a metric space in which the triangle inequality d(x, y) ≤ d(x, z) + d(z, y) is replaced by the stronger inequality d(x, y) ≤ max{d(x, z), d(z, y)}. Ultrametricity is a natural property of “hierarchical” or tree-structured data, for example phylogenetic trees representing distances between species with a constant rate of evolution Durbin et al. (Ch. 7) [28].

In a particular data set, distances between data points might not be perfectly ultrametric, but nevertheless be more or less close to ultrametric. The most direct way of measuring ultrametricity in a data set is to count the fraction of triples of vectors in the data that satisfy the ultrametric inequality, which is what we have termed the “ultrametric triangle fraction”. This value would then range from 1 for perfectly ultrametric data, down to 0 for data in which no triples at all satisfy the ultrametric inequality (although it would be expected in random data to have some number by chance so the value would be unlikely to ever be exactly 0). Murtagh²⁷,²⁹,³⁰ introduces a variant of this technique which uses angles rather than distances in order to avoid lack of invariance due to the use of distances²⁹; however this technique requires a scalar product in the vector space, which in the case of our Hamming distances between culture vectors would require a further step of embedding the data in a Euclidean space²⁷.

An alternative technique to measure the degree of ultrametricity is instead to measure the deviation of the intervector distances in the data from a constructed ultrametric, for example a single-linkage clustering (equivalent to the minimum spanning tree) as is done in Rammal et al. [26] and Rammal et al. [20]. The cophenetic distance between two data points in a hierarchical clustering (often represented as a dendrogram) is the intergroup similarity at which they are first combined into a single cluster. The cophenetic distances created by a hierarchical clustering procedure such as single-linkage, complete-linkage or UPGMA (average-linkage) are ultrametric.

The degree of ultrametricity of (pairwise distances between) a set of data points can then be measured by the cophenetic correlation coefficient³¹,³²,³³: the correlation between the (ultrametric) cophenetic distances induced by the hierarchical clustering and the original distances in the data. Other measurements of the degree of ultrametricity include Rammal's 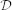²⁶, Lerman's H-classifiability (Lerman et al. [34], as described in Murtagh [29]) and Murtagh's γ³⁰. In this paper, we measure the degree of ultrametricity of a data set using the cophenetic correlation coefficient with single-linkage clustering of the data and Pearson's correlation.

Empirical, permuted, simulated and random data

The first set of empirical data we use is the Eurobarometer survey data of opinions on science and technology³⁵,³⁶,³⁷, as used in Valori et al. [19]. Similarly (but not identical) to Valori et al. [19], we used the survey responses for opinions on science and technology from the Eurobarometer survey data, as well as shuffled data, in which the answers for each question are randomly permuted among the individuals, and uniform random responses. The second set is the General Social Survey (GSS) 1993 data²⁵, which we process in the same way. More details are in the Supplementary Information.

In addition, we use random data generated so as to have the same covariance structure as the real data. This is achieved by using the product of the Cholesky decomposition of the correlation matrix and a normally distributed random vector, that is, the matrix-vector product U^T z where Σ = U^TU is the Cholesky decomposition of the correlation matrix Σ of the original data and 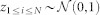. We also permute this simulated data, in the same manner as the real data.

Generated ultrametric data

The “neutral evolution” scheme starts with an initial random vector. We then create two children, by changing up to 50% of the traits in each one to a random value. We do this recursively with the two child vectors, and stop when enough vectors have been created. This is like the process of neutral evolution with a constant rate of evolution (“molecular clock”), but with culture vectors instead of DNA (or protein) sequences. This is exactly the condition under which UPGMA produces a valid phylogenetic tree (i.e. the leaf sequences/vectors are ultrametrically distributed).

In the “prototype evolution” scheme, initial culture vectors are evolved from a set of initial prototype vectors. “Prototype” in this context is akin to an ideal type, or a profile that is the most typical of a category. A cultural prototype may be provided by the first person that has articulated a set of ideas and practices, or a classic text that has founded a set of cultural ideas and practices. Given that cultural information is by definition socially transmitted from an individual to another and that this transmission is imperfect (for example Kashima [38]), it is theoretically reasonable to simulate the distribution of individual profiles within a cultural space as a result of probabilistic deviations from such cultural prototypes. Once a distribution of culture vectors are generated, the centroid that represents the central tendency of the distribution can be thought of as the prototype in the sense used by Rosch & Mervis [39].

Therefore k “prototype” vectors are created with random values, and the remaining N − k vectors are created by choosing at random one of the k prototype vectors, and creating a new vector by copying the prototype and then changing up to 50% of the traits, chosen randomly, to a random value. Hence the vectors created in this scheme form k clusters by construction. We use k = 3 in the results presented here, on the basis that theories of cultural prototypes tend to be built on three to five prototypes, for example Triandis [22], Shweder et al. [40], Fiske [41], Fiske [42], Graham [43].

The “trivial ultrametric” scheme generates vectors that are by construction perfectly ultrametric. It does so by creating (q − 1)F vectors, each of which is all zero apart from the ith element which is set to j, for 1 ≤ i ≤ F and 1 ≤ j < q (a single i and j for each vector). Then N of these vectors are sampled (without replacement) randomly. This creates a set of vectors in which each differs from all the others in exactly two positions, and therefore the intervector distance between any pair of vectors is the same. This data is therefore perfectly ultrametric, but in a “trivial” sense, due to all the intervector distances being equal.

Details of the three schemes are given in the Supplementary Information.

Author Contributions

A.S. and Y.K. wrote the manuscript. A.S., G.R., Y.K. and M.K. all contributed to designing the research. A.S. performed the computer simulations and data analysis. All authors reviewed the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information for Ultrametric distribution of culture vectors in an extended Axelrod model of cult