Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 May 2.
Published in final edited form as: Spat Spatiotemporal Epidemiol. 2010 Mar 20;1(0):117–122. doi: 10.1016/j.sste.2010.03.004

On the effect of diagnostic misclassification bias on the observed spatial pattern in regional count data – A case study using West Nile virus mortality data from Ontario, 2005

Olaf Berke a,*, Lance Waller b
PMCID: PMC4007208  NIHMSID: NIHMS556771  PMID: 22749468

Abstract

Geographic epidemiology is concerned with the investigation of spatially referenced data to discover spatial patterns in the health status of populations. In this context it is generally assumed that a perfect diagnostic test is used to classify individuals as being positive or negative, meaning the health status is measured without error. In this work the effect of an imperfect diagnostic test on spatial patterns of disease in regional count data is investigated in a case study. Specifically the misclassification effect on the semivariogram, Moran’s I statistic and the spatial scan test are evaluated for the situation of West Nile virus infections among dead birds sampled from the 30 public health units of southern Ontario in 2005. We illustrate that under large sample conditions no serious spatial bias is introduced by use of an imperfect diagnostic test as long as the imperfection itself is spatially unbiased.

Keywords: West Nile virus, Scan test, Moran’s I, Semivariogram, Diagnostic test, Misclassification bias

1. Introduction

Geographic epidemiological methods are used to identify, describe, and quantify spatial patterns in the distribution of health status data. This is of particular importance for surveillance of emerging diseases, i.e. in situations of generally unknown disease etiology. If spatial patterns such as trend, clustering or clusters are identified these might suggest clues to testable hypotheses about an unknown disease etiology.

Emerging diseases are characterized by any of the following situations (see also Brown, 2004):

  1. Appearance of a previously unknown disease agent.

  2. Occurrence of a known disease in a new species that was previously deemed to be unsusceptible.

  3. A known disease with increasing incidence over and above its endemic level.

  4. A known disease spreading into a new geographic region and affecting a new population.

In all these situations diagnostic tests are either not fully developed or not properly calibrated for the population under study. Furthermore, such screening tests typically see application in disease surveillance of larger populations. Thus screening tests have to be less expensive and hence are often of less diagnostic quality resulting in larger amounts of false positives and/or negatives. It is often good practise to confirm positive test results by additional (and often however more expensive) tests.

West Nile virus (WNv) is the agent of an emerging zoonosis that has been known since 1937 and caused various outbreaks among human and animal populations in the Mediterranean basin over the past four decades (Zeller and Schuffenecker, 2004). In North America WNv appeared first in dead birds in New York in 1999. Subsequently WNv spread across the continent. In Canada a national surveillance program detected WNv first in dead birds in Ontario in 2001. The first human cases in Ontario were recorded for 2002 (Beroll et al., 2007).

Dead bird surveillance in southern Ontario is organized at the public health unit (PHU) level. In each of the 30 health units only the first four positive dead birds are confirmed by a second test. The main purpose of the surveillance program is to inform when and where WNv occurs. Dead bird surveillance has also been suggested as a means for early warning systems in public health, which allows initiating preventive measures with 10–14 days lead time of human cases (Loeb et al. 2005). This assumes that high-risk areas can be identified using the given data. However, in applications, detailed consideration of the impact of sensitivity and specificity of the screening test often is neglected (Beroll et al., 2007; Mostashari et al. 2003).

In this work observed dead bird mortality fractions due to WNv infections in Ontario of 2005 are adjusted to true mortalities using the method proposed by Rogan and Gladen (1978). This allows an investigation of the misclassification effect of the diagnostic system on the semivariogram, Moran’s I and spatial scan statistic. While results are specific to our data, the case study helps identify general concepts for future study.

2. Material and methods

In this section we give a short description of the study area, followed by key characteristics of the diagnostic test procedure. In particular, we summarize the Rogan and Gladen approach to adjust imperfect test results. We also motivate our choice of the spatial statistics considered in this investigation including a brief description of each.

2.1. Study area

Southern Ontario is the most densely populated area in Canada, home to more than one third of all Canadians. The area is subdivided into 30 PHU’s. The study area stretches out from southwest to northeast over a distance of about 600 kilometres (km).

2.2. Diagnostic method

The screening test used for dead bird surveillance in Ontario is the VecTest©. This test has been described and evaluated in various publications with varying results for the sensitivity (SE) and specificity (SP). Lindsay et al. (2003) report the sensitivity and specificity of the test at a level of 83.9% and 93.6%, respectively. Stone et al. (2005) report a slightly lower sensitivity of 82.1% and perfect specificity of 100%. Another reference for the quality of the VecTest© is the WNV preparedness plan of the Ontario Ministry of Health and Long-Term Care (MOHLTC, 2007), in that report the test is considered 85% sensitive and 95% specific when applied to crows only. For the Ontario dead bird surveillance the first four positive birds in each Health Unit were confirmed by polymerase chain reaction (PCR), which is considered the gold standard test (Lindsay et al., 2003).

2.3. Rogan and Gladen data adjustment method

Rogan and Gladen (1978) proposed an adjustment of the observed disease frequency (OF) given the quality of a diagnostic test, i.e. its sensitivity and specificity to gain the projected or true disease frequency (TF):

TF=(OF+SP−1)(SP+SE−1). (1)

The disease frequency under study can be any measure, e.g. prevalence, incidence or as in the present study the dead bird mortality fraction. When applying this formula care must be taken in situations where disease frequency is less than 1 – SP. Then the numerator in Eq. (1) becomes negative and so does the true disease frequency. The exceptions are situations where SE + SP < 1, i.e. when the diagnostic test device is of unacceptable low quality. This has been observed in several applications and regarded as an effect resulting from unexpected population characteristics for which the test system was not calibrated.

2.4. Statistical methods

It is natural to visualize the spatial variation of regional data such as mortality fractions in form of choropleth maps (Berke, 2001). However with regionally varying sample sizes (and resulting heterogeneity in local variance), often one smoothes the data before mapping. Empirical Bayes smoothing is common practice, especially since this can be interpreted as a way of internal standardization of regional disease frequencies (Berke, 2004). Furthermore, smoothing has a variance stabilizing effect on the frequencies. Such stabilization is an important feature for semivariogram estimation (Berke, 2004) and has also motivated a modification of the Moran’s I coefficient (Assunção and Reis, 1999), in order to avoid spurious results based on local extreme values. The balance between variance stabilization and detection of local high rates is delicate and here we err on the side of stabilizing local rates before assessing for clustering. By doing so we focus on general summaries of spatial patterns but do give up some direct interpretation of both the semivariogram and Moran’s I in favour of avoiding instable local rates. Both statistics: the semivariogram and Moran’s I allow inferences about clustering of disease. Moran’s I is a coefficient to measure the strength of spatial correlation in regional data and provides also a test for disease clustering. The semivariogram is a function of distance providing further insight into the form of disease clustering. Its range parameter informs about the average distance over which individuals are related. Further, if the semivariogram does not level off and posses no sill a spatial trend pattern might be present in the data. The semivariogram can also be instrumental in estimating Moran’s I as follows. Estimation of Moran’s I is based on choosing an appropriate neighbourhood definition for the disease under study. Among others this neighbourhood can be based on distance and especially Euclidean distance between the geographical centres of the PHU’s. In the following we use the estimated range of the semivariogram to define the neighbourhood for Moran’s I. More specifically, we consider neighbourhoods defined by those PHUs whose centre point falls within a circle with radius equal to the semivariogram range and centered at the centre of any particular PHU. It is the radius of the circle that includes the centres of all neighbouring PHU’s. Moran’s I is used here as proposed by Assunção and Reis (1999), i.e. the empirical Bayes estimated mortality fractions are used rather than case counts. See Waller and Gotway (2004) for a review and further details about Moran’s I statistic and the semivariogram. In this case we fit the semivariogram following a model-based approach: the exponential model without a nugget effect parameter with range and sill estimated via maximum likelihood (Diggle and Ribeiro, 2007).

Besides clustering and overall patterns of trend, which represent global characteristics of the disease, the existence and location of localized spatial disease clusters in the study population are of interest in geographic epidemiology. This is most commonly investigated via the circular spatial scan test (Kulldorff, 1997), which we applied to our raw count data. For a review of variants of spatial scan tests and their alternatives see Waller and Gotway (2004). The result of the spatial scan test can depend on the maximum cluster population size. This parameter is fixed by the practitioner with respect to the characteristics of the disease and sampling frame under study. Typically, one allows the maximum population size to vary between the smallest regional sample size and a maximum of 50% of the total population. If the parameter is chosen too small only a part of a cluster is detected. On the contrary if the parameter is chosen too large, neighbouring but separate clusters may be identified as one larger cluster. For exploratory purposes one can explore the effect of varying maximum cluster population sizes; as we do below. When using the scan statistic, as a significance test the maximum cluster population size must be fixed at the beginning of the study, i.e. before a map of the data is generated so any dependence on this choice is important to understand.

For comparison all statistical analysis will be based on the observed and true dead bird mortality fractions. Their differences will be attributed to differential misclassification bias (Rothman et al., 2008) as a result of employing an imperfect diagnostic test.

All statistical analysis and mapping was performed in R (R Development Core Team, 2009), with the exception of cluster detection using the spatial scan test, which was carried out in SaTScan™ (Kulldorff and Information Management Services, 2007).

3. Results

3.1. Data description

Overall a total of 272 out of 1017 dead birds were screened for WNv antibodies and found positive. This results in an observed dead bird mortality fraction of 26.7%, with a 95% confidence interval ranging from 24.1% to 29.5%. The observed mortality at the level of the 30 PHU’s ranged from 3% to 80%, around a regional mean mortality of 27.8% with a variance of 0.043. The sample size per PHU ranged from 8 to 75 dead birds.

Estimating true mortalities for the various PHU’s based on sensitivity and specificity as reported by Lindsay et al. (2003) will produce for some PHU’s negative frequencies. Thus a sensitivity of 82.1% and specificity of 100% as reported by Stone et al. (2005) were used in estimating true mortalities. This gave an overall true mortality of 31.1%. The mean over the true regional mortalities is 33.9%, with a variance of 0.064.

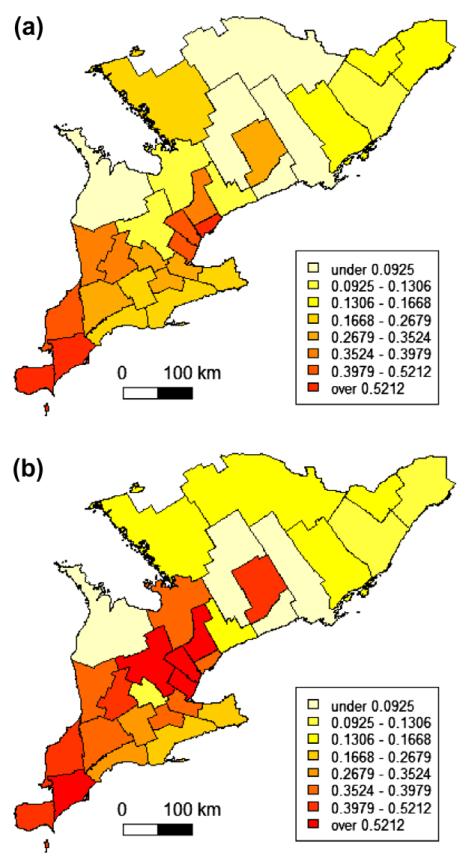
Next the non-rare observed and true regional mortalities were smoothed by empirical Bayes estimation under the Binomial model (Martuzzi and Elliott, 1996). The respective choropleth maps are depicted in Fig. 1. For comparison the same colour scaling was applied in both maps.

Fig. 1.

Fig. 1

Open in a new tab

Choropleth maps of observed (a) and true (b) dead bird mortality fractions due to West Nile virus for 30 Public Health Units in southern Ontario, 2005.

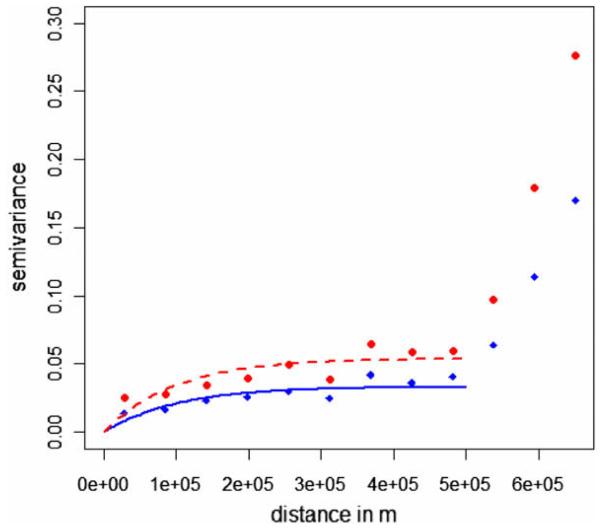
Based on previous results (Beroll et al, 2007) the smoothed data were modeled without spatial trend, i.e. an ordinary kriging model was fit including an exponential semivariogram model. As noted above, we apply the approach to the smoothed data giving up some of the standard interpretation of spatial prediction in favour of stabilized rate estimates. Here we focus on the elements of the estimated semivariogram rather than the typical kriging application of predictions at any location. Any potential trend effects visible in the southwest of the study area (Fig. 1) are regarded as reflections of spatial disease clusters. A nugget effect was not modeled with the already smoothed data but set to 0. The intercept of the fitted ordinary kriging model representing the average mortality over the study area was estimated at a level of 25% for the observed and 28% for the true smoothed mortalities. The practical range was estimated to be 100 and 98 km for the observed and true smoothed mortalities, respectively. The sill represents the overall variance and was estimated at 0.033 and 0.054 for the observed and true smoothed mortalities, respectively. Fitted semivariogram models for the observed and true smoothed mortalities are visually compared in Fig. 2. This shows a proportional effect besides a clear indication for spatial clustering up to a distance of 100 km.

Fig. 2.

Fig. 2

Open in a new tab

Empirical and maximum likelihood fitted exponential semivariogram suggesting a proportional effect for the observed and true dead bird mortality fractions due to West Nile virus for 30 Public Health Units in southern Ontario, 2005. The scale on the x-axis is in meter. Filled circles and a broken line represent the semivariogram of the true dead bird mortality fraction; diamonds and a solid line show the observed data semivariogram.

The range of 100 km defined the neighbourhood for Moran’s I statistic. Its estimate for the observed and true mortalities was 0.37 and 0.36, respectively. In both situations the coefficient was highly significant (simulation based p < 0.01) and is clearly indicating disease clustering.

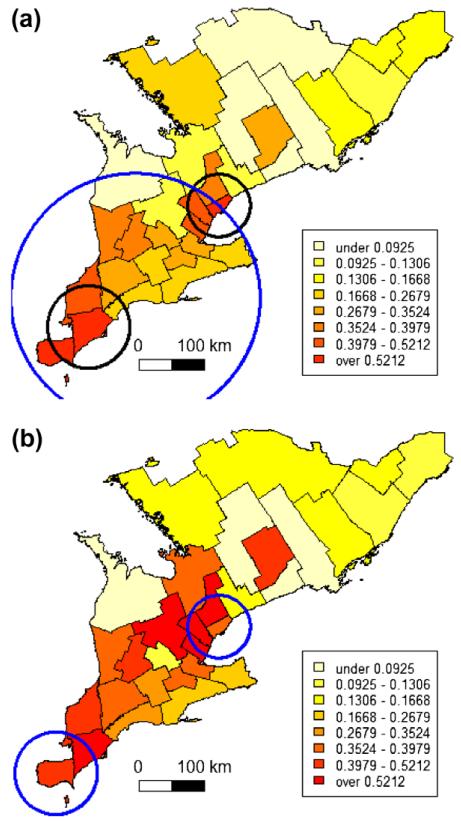
Lastly the misclassification effect on the spatial scan statistic is investigated by exploring the population for possible disease clusters with varying maximum cluster population sizes. When a cluster size of up to 50% of the population at risk was allowed, the scan statistic detected one big cluster in the southeast for the observed mortalities, but two smaller clusters for the true mortalities. The diameter of the circular cluster in the observed data is however suspiciously large, when compared to the semivariogram range of 100 km. Therefore (and for reasons elaborated below) the scan statistic was applied again with smaller maximum cluster population sizes of 40% and 30%. Then two clusters were indicated in similar locations for the observed and true mortalities. Furthermore the circular windows of the primary and secondary cluster as indicated by the spatial scan test had a diameter of 96 and 124 km, respectively. Fig. 3 is summarizing the scan analysis results.

Fig. 3.

Fig. 3

Open in a new tab

Choropleth maps of observed (a) and true (b) West Nile virus dead bird mortality in southern Ontario 2005 with disease clusters identified by the circular spatial scan statistic. In (a) the large circle indicates the location of a single cluster in the observed mortalities and is based on a maximum cluster population size of 50%. The two smaller circles correspond to clusters identified with a maximum cluster population 30% or 40%. In (b) the two circles indicate cluster location in the true mortalities as with a maximum cluster population size of 50%, 40% or 30%.

4. Summary and discussion

Our analysis illustrates the importance of assessments of spatial validity within geographic epidemiology studies. Spatial data can be erroneous for at least two reasons: (i) the data location is incorrect, and (ii) the recorded data value is incorrect. The first issue relates to geocoding of health data and is addressed in several studies. For a recent summary see Rushton et al. (2008). The second issue occurs in geographic epidemiology due to differential misclassification bias as considered in this work. Imperfect diagnostic test devices will on average misclassify a certain percentage of the sample, hence systematically generate false positives and/or false negatives. In consequence the value of geographic epidemiological studies might be questioned: are disease clusters real or just clusters of diagnoses so-called phantom clusters (Jacquez, 2009) based on false positives?

The investigation of diagnostic misclassification bias on spatial statistics using WNv surveillance data from 30 PHU’s in Ontario, 2005, revealed some interesting general results:

  1. the estimate of the disease frequency and its variance are biased, but

  2. disease maps show similar patterns in the distribution of disease frequency

  3. the spatial dependence structure and strength are not seriously affected, and

  4. the detection and location of disease clusters is not affected either.

The specific results depend on the sensitivity and specificity values used in the Rogan and Gladen approach Eq. (1). Here a perfect specificity is assumed and thus within this framework misclassification can only result in false negatives. Therefore the overall true dead bird mortality fraction is underestimated by the observed mortality. Similarly the variance is underestimated as expected by the mean-variance relationship for binomial data. This bias can vary in strength and direction for other situations depending on sensitivity and specificity of the test as well as the disease frequency in the population-at-risk.

The effect on the disease map in this study is not serious: the spatial pattern in the geographic distribution of the observed and true mortality is very similar, though on different average levels. As estimated by the intercept of the ordinary kriging model the average observed mortality is 25% compared to 28% for the average true mortality.

Moran’s I and the semivariogram are two statistics to investigate clustering of disease. Moran’s I correlation coefficient is only marginally different for the observed and true mortality data, i.e. 0.37 and 0.36, respectively. Correlations are not affected by a mean shift in the data. Correspondingly the semivariogram models show a proportional effect (Fig. 2). This means the observed and true mortalities exhibit the same spatial structure: the practical range is about 100 km, only the sill is different. As can be expected with an about 50% underestimated variance between the regional mortalities, the sill is underestimated by about 50% when based on observed and true mortality data. Overall these findings correspond well with what is depicted in the choropleth maps (Fig. 1): the spatial patterns are very similar, but at different mortality levels.

For the spatial scan statistic, which is used to locate the most likely disease cluster, it appears the statistic is relatively robust to misclassification bias. For both the observed and the true mortalities two disease clusters were identified in about the same areas (Fig. 3). One of the two clusters included an extra PHU when based on the observed mortalities; the other cluster was identical for the observed and true mortality data. However choice of the maximum cluster population appears to be a critical parameter with this statistic. Making no further assumptions and using the default value of 50% identified a far too large cluster for the observed mortalities. The diameter of the cluster becomes about 300 km. The smaller cluster based on more realistic and thus smaller maximum cluster sizes had an approximately 100 km diameter, which is in agreement with the semivariogram range. From an ecological perspective it is also expected that infected viremic birds do not travel far, but die soon and this perspective can (and perhaps should) inform our defined neighbourhood size.

The results may not surprise, as it is clear from Eq. (1) that the true disease frequency is a linear transformation of the observed disease frequency. Furthermore the results refer to large sample situations where all regions of the study area are affected to the same degree by misclassification bias. This means the same proportion of misclassified individuals was assumed for all regions. This assumption is unrealistic with small or moderate samples. And as in practise the proportion of misclassified individuals is varying from region to region, it might be possible that phantom clusters of purely false positives are detected. Therefore it is of interest to run simulation studies to further investigate the potential misclassification problems. Random assignment of false positives and false negatives might reveal some insight into the minimum sample size needed to avoid misclassification bias in statistics for spatial patterns of disease.

There is often uncertainty about the quality of diagnostic tests. Though sensitivity and specificity are often regarded as characteristics of a diagnostic test their values depend on the agent and population as well. Therefore it might be worthwhile to employ this uncertainty in a Bayesian framework, see Branscum et al. (2004).

The study presented here is based on regional count data and a few strategically chosen statistics; an extension to point data and further statistical methods is obvious and forms another direction for future research.

5. Conclusion

Misclassification bias potentially affects all epidemiological studies and an assessment of its impact is a key element of epidemiologic research. This study explored this in a geographic setting, examining the effect of systematic diagnostic misclassification bias on spatial statistics used to identify geographic patterns in disease occurrence. The statistics investigated are the (i) spatial scan test which is used to identify disease clusters, (ii) the Moran’s I coefficient to measure the strength of spatial correlation, and (iii) the semivariogram used to describe the spatial dependence structure.

While large sample results indicate that spatial statistics commonly used to investigate geographic patterns of disease are not seriously affected by diagnostic misclassification bias, some impact is apparent and simulation studies are needed to quantify specific effects for finite sample situations.

Acknowledgements

The research by the first author was supported by Grant 200017 from the Ontario Ministry of Agriculture, Food and Rural Affairs.

References

  1. Assunção RM, Reis EA. A new proposal to adjust Moran’s I for population density. Stat Med. 1999;18:2147–62. doi: 10.1002/(sici)1097-0258(19990830)18:16<2147::aid-sim179>3.0.co;2-i. [DOI] [PubMed] [Google Scholar]
  2. Berke O. Choropleth mapping of regional count data of Echinococcus multilocularis among red foxes in Lower Saxony, Germany. Prev Vet Med. 2001;52:119–31. doi: 10.1016/s0167-5877(01)00246-x. [DOI] [PubMed] [Google Scholar]
  3. Berke O. Exploratory disease mapping: kriging the spatial risk function from regional count data. Int J Health Geogr. 2004;3:18. doi: 10.1186/1476-072X-3-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Beroll H, Berke O, Wilson J, Barker IK. Investigating the spatial risk distribution of West Nile virus disease in birds and humans in southern Ontario from 2002 to 2005. Popul Health Metr. 2007;5:3. doi: 10.1186/1478-7954-5-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Branscum AJ, Gardner IA, Johnson WO. Bayesian modeling of animal- and herd-level prevalences. Prev Vet Med. 2004;66:101–12. doi: 10.1016/j.prevetmed.2004.09.009. [DOI] [PubMed] [Google Scholar]
  6. Brown C. Emerging zoonoses and pathogens of public health significance - an overview. Rev Sci Tech Off Int Epiz. 2004;23:435–42. doi: 10.20506/rst.23.2.1495. [DOI] [PubMed] [Google Scholar]
  7. Diggle PJ, Ribeiro PJ. Model-based geostatistics. Springer; New York: 2007. [Google Scholar]
  8. Jacquez GM. Cluster morphology analysis. Spat Spatio-temporal Epidemiol. 2009;1:19–29. doi: 10.1016/j.sste.2009.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Kulldorff M. A spatial scan statistic. Commun Stat B. 1997;26:1481–96. [Google Scholar]
  10. Kulldorff M. SaTScan™ v. 7.0.2: Software for the spatial and space-time scan statistics. Information Management Services, Inc.; 2007. URL http://www.satscan.org. [Google Scholar]
  11. Lindsay R, Barker I, Nayar G, Drebot M, Calvin S, Scammell C, et al. Rapid antigen-capture assay to detect West Nile virus in dead corvids. Emerg Infect Dis. 2003;9(11):1406–10. doi: 10.3201/eid0911.030318. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Loeb M, Elliott SJ, Gibson B, Fearon M, Nosal R, Drebot M, et al. Protective behaviour and West Nile virus risk. Emerg Infect Dis. 2005;11:1433–6. doi: 10.3201/eid1109.041184. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Martuzzi M, Elliott P. Empirical Bayes estimation of small-area prevalence of non-rare conditions. Stat Med. 1996;15:1867–73. doi: 10.1002/(SICI)1097-0258(19960915)15:17<1867::AID-SIM398>3.0.CO;2-2. [DOI] [PubMed] [Google Scholar]
  14. MOHLTC West Nile virus preparedness and prevention plan 2007. 2007 Online available at: http://www.health.gov.on.ca/english/public/pub/ministry_reports/wnv_plan_2007.
  15. Mostashari F, Kulldorff M, Hartman JJ, Miller JR, Kulasekera V. Dead bird clusters as an early warning system for West Nile virus activity. Emerg Infect Dis. 2003;9:641–6. doi: 10.3201/eid0906.020794. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. R Development Core Team . R: A language and environment for statistical computing. R Foundation for Statistical Computing; Vienna, Austria: 2009. http://www.R-project.org [Google Scholar]
  17. Rogan WJ, Gladen B. Estimating prevalence from the results of a screening test. Am J Epidemiol. 1978;107(1):71–6. doi: 10.1093/oxfordjournals.aje.a112510. [DOI] [PubMed] [Google Scholar]
  18. Rothman KJ, Greenland S, Lash TL. Modern epidemiology. 3rd ed. Lippincott, Williams & Wilkins; Philadelphia: 2008. [Google Scholar]
  19. Rushton G, Armstrong MP, Gittler J, Greene BR, Pavlik CE, West MM, et al. Geocoding health data: the use of geographic codes in cancer control, research and practice. CRC Press/Chapman and Hall; Bocca Raton: 2008. [Google Scholar]
  20. Stone WB, Therrien JE, Benson R, Kramer L, Kauffman EB, Eidson M, et al. Assays to detect West Nile virus in dead birds. Emerg Infect Dis. 2005;11(11):1770–3. doi: 10.3201/eid1111.050806. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Waller LA, Gotway CA. Applied spatial statistics for public health data. Wiley; New York: 2004. [Google Scholar]
  22. Zeller HG, Schuffenecker I. West Nile virus: an overview of its spread in Europe and the Mediterranean basin in contrast to its spread in the Americas. Eur J Clin Microbiol Infect Dis. 2004;23:147–56. doi: 10.1007/s10096-003-1085-1. [DOI] [PubMed] [Google Scholar]

RESOURCES