Rebuttal to a Comment by Richard E. Waugh on our Article “Yield Strength of Human Erythrocyte Membranes to Impulsive Stretching”

We thank the author of a comment in this issue of the Biophysical Journal for highlighting a common challenge in assessing the true shape of a three-dimensional object such as a red blood cell from microscopic images. This is a problem for our work (1) as well as for the reference called out in the comment, Fung et al. (2). In the latter work, they assumed an a priori parametric shape to which they fit their interferometric measurements and thus do not measure the thickness independently.

The author of the comment (3) states that, due to not accounting for the changes in cell thickness during the stretching, we severely overestimate our areal strain measurements. He states as an example that the pressing of a biconcave cell into a flat shape against a rigid surface would not lead to areal strain, but to an increase in projected area. He continues that, because we only measure projected areas, our measurement may be flawed. Below, we provide support that the cells are indeed stretched largely. The example given by Richard Waugh, does not apply to our experiment. In our experiments, the cells are strained parallel to a rigid wall. Thus, the cells are experiencing a shear flow and not normal forces as stated in the comment.

The author of the comment suggested us to apply a constant volume constraint of the cell to proof our reported large strain vales. We gladly follow his suggestion, and have reevaluated some of our data. Unfortunately, the absolute volume of the cell is not available from the microscopic pictures. Therefore, we have to assume some value to determine the thickness of the cell in its final (relaxed) state. During the stretching the thickness will change, but can now be estimated from the constant volume assumption. The cell volume is thus the measured projected area times the thickness, i.e., the cell shape is assumed as a right prism with a fixed volume of 98 μm³ (2). Fig. 1 compares the areal strain, S_v, from 14 cells using the constant volume assumption with the original data, S₀, which ignored a change in thickness. For moderate changes of the projected area, i.e., <∼35%, the values of areal strain are similar. For larger areal strain, the method used in our article is overestimating the stretching by roughly 40–50%.

Figure 1.

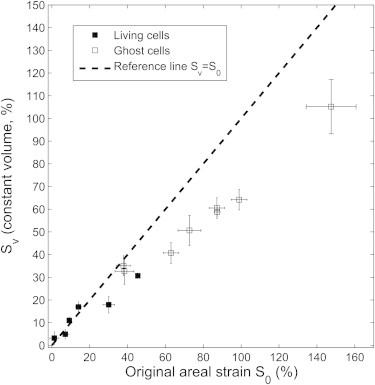
Comparison of the areal strain from 14 cells using the constant volume assumption, S_v, with the original data, S_o, which neglected a change in thickness. (Squares with error bars) Calculated S_v versus each measured S₀ for living (solid squares) and ghost (open squares) cells. Here, for each cell, S₀ is measured four times by using different start points for the snake algorithm under the same threshold as in Fig. 4 of Li et al. (1).

This analysis supports two main findings: very large areal strain can be achieved; and stretching of up to 30%, if done sufficiently fast, may not lead to cell death.

We agree with the critiques that varying the threshold in gray levels of the image may considerably alter the estimated area. That is why we use the same threshold for all experiments summarized in Fig. 4 of Li et al. (1). Fig. S4, found in the Supporting Material of Li et al. (1), shows the resulting contour for this threshold. The figure in question (Fig. S5 of Li et al. (1)) serves another purpose: there we estimate the error for the absolute area measurements for different magnifications. For strain, not the absolute, but the relative change is important. These relative changes of the area can be very accurately tracked if care is taken for proper illumination and in keeping the threshold criteria constant. Then, even very pixelated images, such as the one in our work, allow for accurate estimates of a relative quantity such as a strain. Another example showing the validity of our approach is demonstrated in a very different experiment but with a similar image quality to which we refer (see Fig. 5 of Ohl et al. (4)).

In summary, we demonstrated the validity of our measurements within the experimental means of having only projected images of the three-dimensional cell shape available. The important experimental finding that the area of cells can be stretched largely, here to ∼30% with 50% survival probability, remains.