Abstract
Crystalline micrometer-long YSi2 nanowires with cross sections as small as 1×0.5 nm2 can be grown on the Si(001) surface. Their extreme aspect ratios make electron conduction within these nanowires almost ideally one-dimensional, while their compatibility with the silicon platform suggests application as metallic interconnect in Si-based nano-electronic devices. Here we combine bottom-up epitaxial wire synthesis in ultrahigh vacuum with top-down miniaturization of the electrical measurement probes to elucidate the electronic conduction mechanism of both individual wires and arrays of nanowires. Temperature-dependent transport through individual nanowires is indicative of thermally-assisted tunneling of small polarons between atomic-scale defect centers. In-depth analysis of complex wire networks emphasize significant electronic crosstalk between the nanowires, due to the long-range Coulomb fields associated with polaronic charge fluctuations. This work establishes a semi-quantitative correlation between the density and distributions of atomic-scale defects and resulting current-voltage characteristics of nanoscale network devices.
Keywords: YSi2 nanowires, electronic transport, self-assembly, scanning tunnelling microscopy, polarons
Quantum transport is at the heart of nanoscience and marries a fundamental law of nature, quantum mechanics, with applied electrical engineering and emerging materials technologies. Ultimately, nanoscale electronic devices will contain networks of wires whose cross sections will be so small as to represent one-dimensional conductors with novel transport properties. Among the many intriguing nanowire systems synthesized in recent years, epitaxial metal-silicide nanowires may be the most practical electrical interconnects because of their compatibility with the established silicon platform.1–10 Here, we investigate the electrical properties of ultrathin epitaxial YSi2 nanowires on Si(001) with a four-tip scanning tunneling microscope. Conduction through individual nanowires follows an inverse Arrhenius behavior indicative of thermally-assisted tunneling of small polarons between defect centers. Analysis of individual wire resistances, probe resistances, and negative differential resistances of nanowire networks indicates significant electronic interwire coupling below 150 K. The long-range coupling mechanism involves the dielectric polarization of the substrate, inducing current blockades in neighboring conduction channels. Establishing such semi-quantitative correlations between the density and distribution of atomic-scale defects and resulting current-voltage behavior is a critical first step towards designing novel nano architectures with desirable electrical properties.
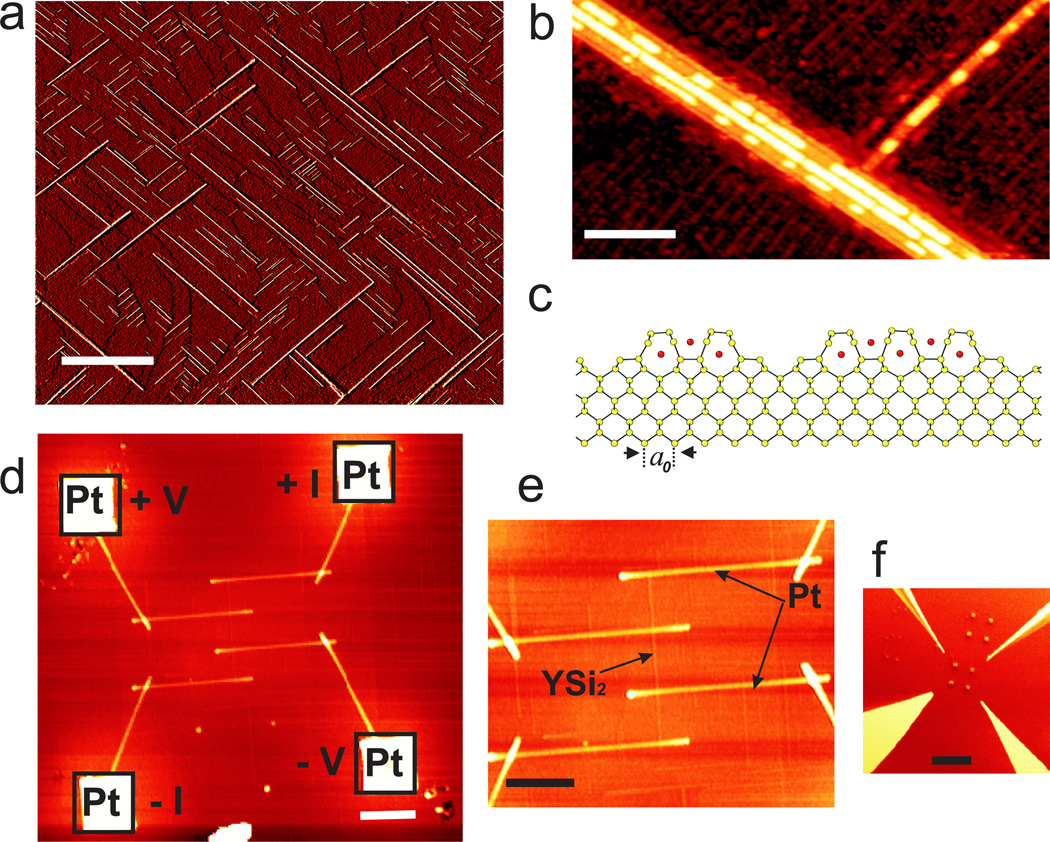
The YSi2 wires are formed by depositing about 0.5 monolayer (ML) yttrium on atomically- clean heated Si(100) substrates in ultrahigh vacuum (UHV). Their formation proceeds in two steps. First, 0.35 ML yttrium is incorporated into a Si(100)(2 × 7) surface reconstruction or template layer.11 The remaining yttrium atoms subsequently self-assemble into epitaxial YSi2 nanowires. The wires grow parallel to the atom rows of the template.9,11,12 Figure 1a is a large-scale scanning tunneling microscopy (STM) image of a Si surface decorated with YSi2 nanowires. Orthogonal wires represent different surface terraces, a consequence of the four-fold symmetry of the (100) substrate. Depending on the growth conditions and deposition amount, the wires are isolated or bundled.12 The widths of individual nanowires are quantized in units of the Si(001) lattice constant (a0 = 0.384 nm), the thinnest being only 3a0 (1.15 nm) wide and about 1 µm long.9
Figure 1.
Scanning probe characterization of YSi2 nanowires. (a) STM image showing numerous YSi2 wire bundles on the Si(100) surface before patterning (scale bar: 450 nm). The tunneling parameters are −1.9 V and 0.08 nA. (b) Enlarged area of panel (a) showing two orthogonal bundles with segments of a second silicide layer (scale bar: 22 nm). (c) Cross-sectional structure of a wire bundle containing a 3a0 and a 5a0 nanowire, according to Ref. 12, with a0 = 0.384 nm; silicon atoms are shown in yellow and yttrium atoms are shown in red. (d) Non-contact atomic force microscopy (AFM) image of a capped YSi2 nanowire contacted by Pt leads and Pt contact pads (squares) (scale bar: 400 nm). (e) AFM image of the center area of the device presented in (d), showing the Pt leads and a YSi2 nanowire bridging the leads (scale bar: 300 nm). (f) Scanning electron microscopy (SEM) image showing four STM tips in close proximity to the Pt pads (scale bar: 5 µm).
The bundles used for our transport studies are all 0.5 nm high. Many of them are decorated with segments of a second silicide layer that show up as bright segments in the STM images of Figure 1b. These bundles can grow several microns long. STM images show that the nanowires inside a bundle are mostly 3a0, 4a0 and 5a0 wide, though wire widths of up to 9a0 are occasionally observed. Figure 1c displays a cross-sectional structure of a bundle containing a 3a0 and a 5a0 nanowire. The strongly uni-directional growth and extreme aspect ratio of these wires are attributed to the perfect lattice match along the [112̄0] direction of YSi2 and [11̄0] direction of the Si substrate, along with the absence of a close lattice match along the other crystal axes.9 A detailed study of the structure and growth was presented in Ref 12.
Electrical transport measurements on these tiny objects pose a formidable challenge, especially in light of the difficulty of establishing reliable probe contacts, and because the wires cannot be decoupled electronically from their surrounding. A four-tip STM apparatus with two outer current contacts and two inner voltage probes13 should in principle eliminate problems related to contact resistances for single nanowires and would furthermore seem ideal for imaging and positioning of the wire and contact probes, respectively, provided that the wires are clearly resolved during probe positioning. However, because of the extremely small dimensions and fragility of these ultrathin nanowires (0.5 nm high), mechanical contact to the STM tips unavoidably damages these wires. To circumvent this problem, we established electrical contact using a four-tip STM in conjunction with nano-lithography. First, we contacted the wires to ultrathin Pt leads, fabricated ex-situ by electron-beam-induced deposition (EBID) in a focused ion beam system (FIB; see Experimental section). To prevent oxidation, the samples were capped with an ultrathin amorphous Si layer prior to removal from UHV. Figure 1d and Figure 1e are AFM images of one of the devices. Here a YSi2 wire-bundle is contacted by four thin Pt electrodes connecting the nanowires to four structurally robust Pt contact pads (squares). Next, we positioned the STM tips onto the contact pads (Figure 1f). The electrical characteristics of the wires were determined by measuring the voltage drop as a function of current for temperatures between 85 K and 300 K. In separate control measurements, we verified that the conductance through the substrate or (2 × 7) wetting layer is negligible in this temperature range (see Supporting Information for further details). In all, we have measured 12 devices in a 4-probe setup. The YSi2 bundles in these studies are 7 to 14 nm wide, as measured with non-contact AFM (see Experimental section).
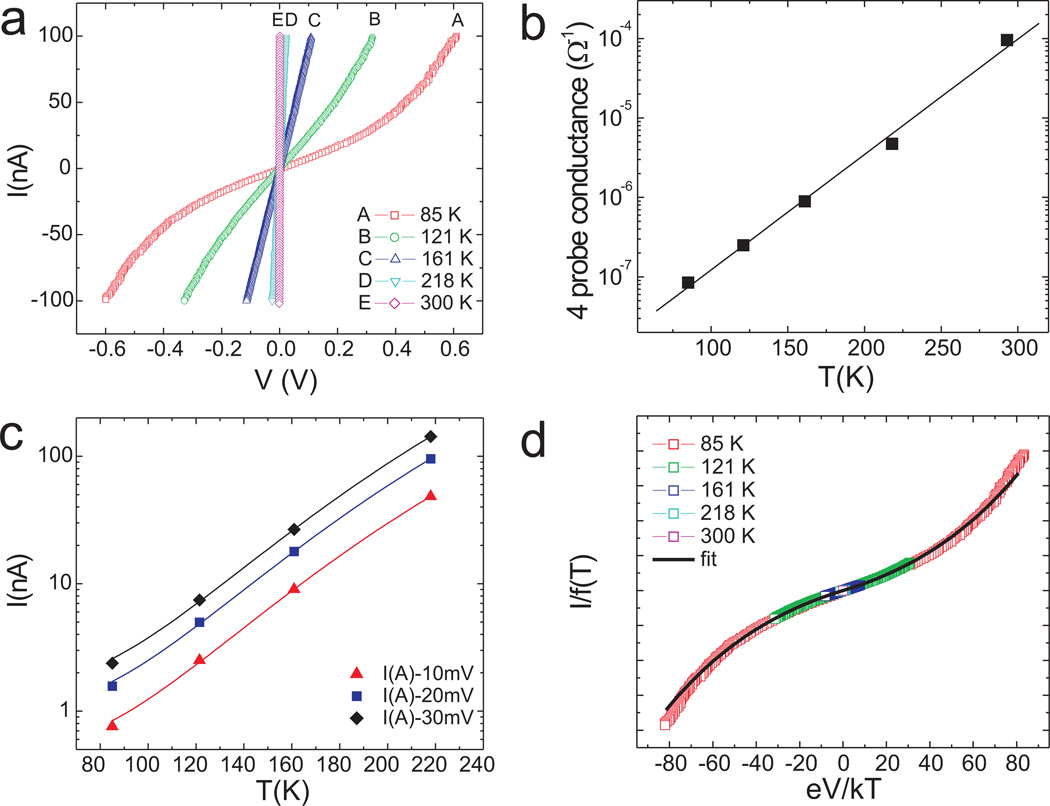
Scanning tunneling spectroscopy studies from uncapped wires suggest that the wire bundles are metallic, as they reveal a finite tunneling density of states at the Fermi level.9,12 Figure 2a displays the transport I – V characteristics for a single bundle device (10 nm wide) for different temperatures, measured with the 4-tip STM. The I – V characteristics are indeed linear at 161 K and above but they are non-linear at 121 K and below. Figure 2b shows the zero-bias conductance as a function of temperature, plotted on a semi-logarithmic scale. The conductance drops over three decades when cooling from room temperature to 85 K.15 This temperature-dependence indicates that the conductance is thermally activated, in spite of the metallicity of uncapped wires.9,12 Nonetheless, the inverse Arrhenius behavior of the wire conductance, i.e. ln σ ∝ T, is highly unusual.
Figure 2.
Transport properties of a YSi2 wire-bundle. (a) I –V characteristics at various temperatures. (b) Temperature dependence of the zero-bias conductance of the YSi2 bundle. (c) (I, T) data plotted for small voltages; solid lines are fits to the data using eq 1.14 (d) I/f(T) plotted against eV/kT for Ip = 0.36 ± 0.02 eV and ℏω = 0.057 ± 0.002 eV. The solid line is a fit to the data using eq 1; the fitting parameter, n, is 50.
So far, the exponential dependence of conductance on temperature has only been observed for disordered films16,17 and for organic monolayers of eicosanoic acid (C20) sandwiched between Pt electrodes.18 The latter was theoretically explained in terms of small polaron hopping via defect centers.14 According to this theory, the current at high temperatures and small bias can be expressed as:
| (1) |
where Ip is the polaron shift, ω is (surface) phonon frequency, and n is the number of defects or impurities in the wire (see Supporting Information for further details). The first two parameters are determined by fitting the (I, T) data at different bias (Figure 2c) to be Ip = 0.36 ± 0.02 eV and ℏω = 0.057±0.002 eV. I(V, T) can then be scaled by plotting I(V, T)/f(T) against eV/kT where f(T) is the voltage independent part of the exponential function in eq (1). The scaled data nicely collapse when using Ip and ω values mentioned above (see Figure 2d). None of the other known transport models, including that of a Luttinger Liquid,19 produced satisfactory results. The small deviations from the fit that are seen for the 85 K data (Figure 2d) for eV/kT > 50 are attributed to the fact that eq 1 is valid in the limit of small voltage.14
The numbers above seem quite reasonable for the YSi2 nanowires as the bonding configurations of the Si atoms in the wires resemble those at reconstructed Si(001) surfaces.9 For instance, the 57 meV phonon frequency is very close to the frequency of the backbond stretching mode of Si dimers on the Si(001)(2×1) surface.20 The polaron shift represents the energy lowering of the defect levels resulting from the local bond deformation or restructuring upon electron capture. For Si surfaces, the polaron shift is indeed expected to be of the order of 0.4 eV.21,22
A fit using eq 1 determines the number of defects or impurities to be 50 for a wire-bundle segment of 314 nm long, i.e., one defect per 6 nm on average. STM images of uncapped wires reveal a defect frequency distribution peaking at one defect per 5 nm per wire when both vacancy and adatom defects (i.e., extra adatoms) are taken into consideration. The close match between the two defect frequencies suggests that vacancy and adatom defects are responsible for the charge trapping.
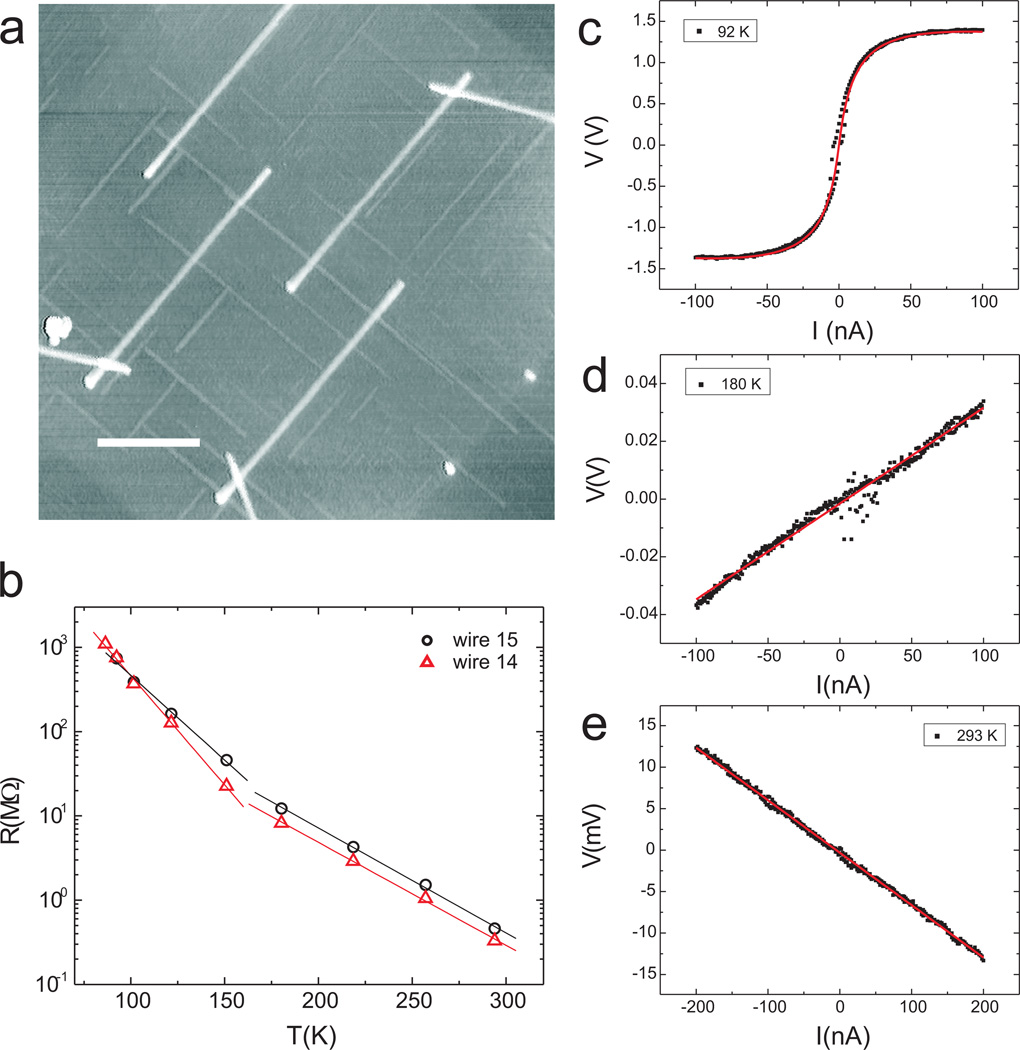
Figure 3a presents an AFM image of the center part of a nanowire network device, where one easily distinguishes multiple YSi2 nanowires in between the Pt electrodes. Figure 3c-e shows three I–V characteristics representative of such a device. To understand the strong S shapes (Figure 3c) and the ’negative resistances’ (Figure 3e) in these devices, we construct a simple resistor network to simulate the experimental wire network and derive a simple nonlinear I – V formula, eq 2, that fits the measurements (see Supporting Information for further details). Here, we assert that the transport through a nanowire is strongly influenced by the long-range Coulomb field in the substrate surface and/or capping layer, emanating from trapped charges at local defect sites.
Figure 3.
Characterization of YSi2 wire network devices. (a) AFM image illustrating one example of a YSi2 network device (wire 15) (scale bar: 370 nm). (b) Temperature dependence of the corrected zero bias resistance (see text) of two YSi2 network devices, wire 14 (Supporting Information) and wire 15. The solid lines represent linear fits. (c), (d), (e) I – V characteristics of a network device (wire 15) at the indicated temperatures. The solid lines represent fits to the data using eq 2.
As an example, we consider two parallel wires, one with a low resistance and the other with a large resistance due to the presence of a strong scattering (defect) center in this wire. As the current increases, the high-resistance wire builds up a local charge that is proportional to the current. The Coulomb field from this charge build-up then creates a scattering potential in the neighboring low-resistance wire. For sufficiently strong coupling this will completely shut off transport in the low-resistance wire. We implemented this concept using two different circuit models and derived a simple nonlinear I – V formula (see Supporting Information for further details):
| (2) |
Equation 2 was fitted to the experimental I – V curves in Figure 3c-e. The fitted ratio B/C is related to the resistances of other YSi2 wire fragments and the Pt leads (measured separately; see Supporting Information). R1 is the contact resistance of one of the voltage probes. We assert that eq 2 has a rather general validity for interacting nanowires where the coupling between the nanowires originates from the long-range Coulomb fields. The particular meanings of the fitting parameters R1, B and C depends on the details of the circuit model. For data measured below 150 K, three parameters B, C, and R1 suffice. But for data measured above 150 K only the slope of the I –V curve can be reliably determined, which gives us (B/C)R1. Following this rationale we can express the corrected nanowire resistance as,
| (3) |
where RC is an effective contact resistance and is estimated from the resistance of the Pt leads. The corrected wire resistance for two devices is plotted in Figure 3b at different temperatures.
The change from nonlinear I –V (or negative resistances) to linear I –V above 150 K reflects the changing interwire coupling constant λ, which vanishes above 150 K. Below 150 K, interwire coupling arises from the dielectric polarization of the substrate (or capping layer) by the charge fluctuations in the wires. The dielectric polarization, in turn, enhances the polaron activation energy (see Supporting Information for further details). This mechanism makes two predictions: 1. There should be two distinct temperature dependences above and below the critical temperature (150 K), corresponding to the polaron activation energies of a single wire and coupled wires, respectively; 2. At the critical temperature the polaron hopping frequency is approximately the transverse optical phonon mode frequency. The first prediction is confirmed by the temperature dependence of the wire resistance in Figure 3b, revealing two distinct slopes. The second prediction can be verified by the relationship between the measured resistance and the polaron hopping frequency in the Supporting Information. At the critical temperature (Tc ≈ 150 K), the measured resistance is R(Tc) ≈ 20 MΩ (for wire 14). From the fitted single wire data we know that the optical phonon energy is approximately ℏωTO ≈ 0.057 eV. Based on density functional theory calculations, the impurity density of states Dimp ≈ 1 eV−1 (see Supporting Information for further details). From these values we find,
| (4) |
This is in good agreement with the fitted value of n = 50 for single wires.
The combination of EBID nano-lithography and four-probe STM is shown to be capable of measuring the transport properties of ultrathin epitaxial nanowires while eliminating contact resistances and minimizing bulk conduction. No doubt, the electrical characteristics of nanowires approaching the one-dimensional limit will always be heavily influenced by atomic-scale charge trapping defects, and the resulting polarization of the surroundings as shown here for the YSi2 wires. This poses severe constraints on the materials quality and circuit designs of future nanoarchitectures. For fundamental studies, it will be highly beneficial to grow both nanowires and nanowire contacts in-situ (UHV), which would allow one to cherry pick wires with certain cross-sectional dimensions and defect configurations. Such studies should be feasible and would pave the way for major achievements in nanoscale electrical engineering.
Experimental
The YSi2 wires were grown in a UHV system with a base pressure of 1 × 10−10 mbar. A sub-monolayer amount of yttrium was deposited by electron-beam evaporation onto an atomically clean Si(001)(2 × 1) substrate held at 625 ± 25°C. STM imaging was carried out with a single-tip Omicron variable temperature VT-STM at room temperature. The wires were protected against oxidation by a thin layer of amorphous silicon prior to air exposure. Pt contacts were deposited using electron-beam induced deposition (EBID) of trimethyl(methylcyclopentadienyl)platinum(IV) on a Helios NanoLab 600 DualBeam focused ion beam (FIB) system (FEI Company). An accelerating voltage and beam current of 10 kV and 21 pA, respectively, were used for the deposition. The Pt contacts have cross-sections of 20 × 20 nm2 and required less than one second each to deposit. Thin contacts and short deposition times were used in order to prevent electron beam-induced damage to the YSi2 nanowires and to minimize the deposition of platinum peripheral to the patterned regions, which could result in leakage currents.23 The (400 × 400 nm2) contact pads were 50 nm thick, i.e. sufficiently thick to withstand potential damage from STM tip contacting. Contact resistances proved to be highly reproducible. For the measurement of electrical transport properties, four STM probes were positioned on the contact pads, guided by SEM.13 Once the probes are close enough to the contact pads, the probes can be placed just a few nm above the contact pads using a controlled tunneling feedback mechanism (typically 4 V, 50 pA at 1 nA/V gain) so as to avoid unwanted crash. After the feedback current is stabilized, the probes are positioned on the contact pads. The outer two probes (Figure 1d) serve as the current contacts and the two inner probes (Figure 1d) detect the voltage drop due to the finite resistance of the nanowires. I –V curves were obtained as a function of sample temperature using a UHV cryostat with built-in counter heater. The temperature was measured with a calibrated silicon diode (Lakeshore, DT-670-SD-4D) and is accurate to within 50 mK. Ex-situ AFM images of the measurement devices were obtained after the transport measurements were completed. The widths of the wire-bundles are extracted from full width at half maximum (FWHM) of the AFM line profiles, after deconvolution following the method described by Villarrubia.24 The tip profiles used for the deconvolution were determined by AFM imaging of an ultrasharp silicon grating sample. Note that the capping layer dilation was not accounted for; we believe the actual widths are slightly smaller than those reported here. The STM and AFM images were analyzed using the WSxM software.25
Supplementary Material
Acknowledgement
We thank Stephen Jesse for his help with the AFM measurements. The experimental research was sponsored by NIH Grant No. R01HG002647 and NSF Grant No. DMR-1005488. A portion of this research was conducted at the Center for Nanophase Materials Sciences, which is sponsored at Oak Ridge National Laboratory by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy (XGZ, THK, PRCK and APL).
Footnotes
Supporting Information Available
Detailed experimental information about the STM characterization of wire-bundles including defect analysis from STM images of uncapped wires, control measurements for transport studies and transport measurements of wire networks. Detailed theoretical information about polaron hoping in a single wire, polarization-induced resistance, temperature dependence of the inter-wire coupling and density functional theory calculations of wire defects.
This material is available free of charge via the Internet at http://pubs.acs.org/.
References
- 1.Preinesberger C, Kalkaand VRS, Dahne-Prietsch M. J. Phys. D. 1998;31:L43–L45. [Google Scholar]
- 2.Preinesberger C, Becker SK, Vandre S, Kalka T, Dahne M. J. Appl. Phys. 2002;91:1695–1697. [Google Scholar]
- 3.Chen Y, Ohlberg DAA, Williams RS. J. Appl. Phys. 2002;91:3213–3218. [Google Scholar]
- 4.Ragan R, Chen Y, Ohlberg DAA, Medeiros-Ribeiro G, Williams RS. J. Cryst. Growth. 2003;251:657–661. [Google Scholar]
- 5.Liu BZ, Nogami J. J. Appl. Phys. 2003;93:593–599. [Google Scholar]
- 6.Nogami J, Liu BZ, Katkov MV, Ohbuchi C, Birge NO. Phys. Rev. B. 2001;63:233305-1–233305-4. [Google Scholar]
- 7.Zhu Y, Zhou W, Wang S, Ji T, Hou X, Cai Q. J. Appl. Phys. 2006;100:114312-1–114312-11. [Google Scholar]
- 8.Yoshimoto S, Murata Y, Kubo K, Tomita K, Motoyoshi K, Kimura T, Okino H, Hobara R, Matsuda I, Honda S, Katayama M, Hasegawa S. Nano Lett. 2007;7:956–959. doi: 10.1021/nl0630182. [DOI] [PubMed] [Google Scholar]
- 9.Zeng C, Kent PRC, Kim TH, Li AP, Weitering HH. Nature Mat. 2008;7:539–542. doi: 10.1038/nmat2209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Qin S, Kim TH, Zhang Y, Ouyang W, Weitering HH, Shih CK, Baddorf A, Wu R, Li AP. Nano Lett. 2012;12:938–942. doi: 10.1021/nl204003s. [DOI] [PubMed] [Google Scholar]
- 11.Liu BZ, Nogami J. Surf. Sci. 2003;540:136–144. [Google Scholar]
- 12.Iancu V, Kent PRC, Hus S, Hu H, Weitering HH. J. Phys.: Condens. Matter. 2013;25:014011-1–014011-12. doi: 10.1088/0953-8984/25/1/014011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kim TH, Wang Z, Wendelken JF, Weitering HH, Li W, Li AP. Rev. Sci. Instrum. 2007;78:123701–123708. doi: 10.1063/1.2821610. [DOI] [PubMed] [Google Scholar]
- 14.Osipov VV, Foygel M, Stewart DR, Williams RS. J. Phys.: Condens. Matter. 2004;16:5705–5712. [Google Scholar]
- 15.Separately, we explored the transport properties of wire-bundles in a two-probe setup, where a single wire-bundle was connected to only two Pt contact pads, down to 100 K. A similar trend was found and the wire conductance dropped as we lowered the temperature. However the conductance changed only one order of magnitude between 300 K and 100 K, suggesting that at high temperatures we were limited by contact resistances. Therefore, a four-probe setup is crucial for measuring the transport properties of thin nanowires where contact resistances can become very large due to the small contact areas.
- 16.Gudaev OA, Malinovsky VK, Paul EE, Treshikhin VA. Solid State Commun. 1990;74:1169–1173. [Google Scholar]
- 17.Vaknin A, Ovadyahu Z, Pollak M. Europhys. Lett. 1998;42:307–311. [Google Scholar]
- 18.Stewart DR, Ohlberg DAA, Beck PA, Lau CN, Williams RS. Appl. Phys. A. 2005;80:1379–1383. [Google Scholar]
- 19.Blumenstein C, Schäfer J, Mietke S, Meyer S, Dollinger A, Lochner M, Cui XY, Patthey L, Matzdorf R, Claessen R. Nature Phys. 2011;7:776–780. [Google Scholar]
- 20.Fritsch J, Pavone P. Surf. Sci. 1995;344:159–173. [Google Scholar]
- 21.Weitering HH, Shi X, Johnson PD, Chen J, DiNardo NJ, Kempa K. Phys. Rev. Lett. 1997;78:1331–1334. [Google Scholar]
- 22.Chen CD, Selloni A, Tosatti E. Phys. Rev. B. 1984;30:7067–7091. [Google Scholar]
- 23.Gopal V, Radmilovic VR, Daraio C, Jin S, Yang P, Stach EA. Nano Lett. 2004;4:2059–2063. [Google Scholar]
- 24.Villarrubia JS. J. Res. Natl. Inst. Stand. Technol. 1997;102:425–454. doi: 10.6028/jres.102.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Horcas I, Fernandez R, Gómez-Rodríguez JM, Colchero J, Gómez-Herrero J, Baro AM. Rev. Sci. Instrum. 2005;78:013705-1–013705-8. doi: 10.1063/1.2432410. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.