The Changing Character of the Black–White Infant Mortality Gap, 1983–2004

Abstract

Objectives. We examined how changes in demographic, geographic, and childbearing risk factors were related to changes in the Black–White infant mortality rate (IMR) gap over 2 decades.

Methods. Using 1983–2004 Vital Statistics, we applied inverse probability weighting methods to examine the relationship between risk factors and 3 outcomes: the overall IMR gap, its birth weight component, and its conditional (on birth weight) IMR component.

Results. The unexplained IMR gap (the part not related to observed risk factors) was stable, changing from 5.0 to 5.3 deaths per 1000 live births. By contrast, the explained gap declined from 4.6 to 1.9. The decline in the explained gap was driven by the changing relationship between risk factors and IMR. Further analysis revealed that most of the unexplained gap occurred among infants weighing less than 1000 grams at birth, whereas most of the explained gap occurred among infants weighing more than 1000 grams.

Conclusions. The unexplained gap was stable over the last 2 decades, but the explained gap declined markedly. If the stability of the unexplained gap continues, even complete convergence of risk factors would reduce the Black–White IMR gap by only one quarter.

One of the most dramatic health disparities in the United States is the infant mortality rate (IMR) gap between Blacks and Whites. The size and persistence of this gap are well-documented.^1,2 To shed light on why the gap exists, numerous studies examined how it is related to birth weight and gestational age. These studies found that the gap in numerous years could largely be accounted for by the much higher rates of low birth weight and preterm births among Blacks, particularly at the smallest and earliest ranges.^3–8 Other studies analyzed how the IMR gap (sometimes disaggregated by cause of death) is associated with differences in risk factors, such as maternal age and education.^9–13

To the extent that infant mortality varies by observed risk factors, some of the IMR gap can be explained by differences in these risk factors between the 2 groups. The unpredicted IMR gap (the part that is unrelated to differences in the observed risk factors) is then a measure of the overall IMR gap net of well-documented differences between Blacks and Whites in measured socioeconomic, geographic, and childbearing characteristics. Documenting the relationship between the explained and unexplained gaps and birth weight can provide important additional information about how the risk factors operate.

Our study examined how changes in the absolute IMR gap and its components were related to changing risk factors over 2 decades, making 3 contributions to the literature. First, we used inverse probability weighting to distinguish between the explained and unexplained IMR gaps, allowing us to provide detailed results regarding how these gaps are related to birth weight. Second, we focused on the trends in the explained and unexplained gaps. Third, we included state of birth as a risk factor because many important inputs for the production of healthy infants vary by state and there are substantial differences between the geographic distributions of White and Black births.¹⁴

METHODS

In this section, we describe the data and our baseline analytic choices. We discuss results based on several important alternative choices in the Sensitivity Analysis section. Further details on the data and methods are provided as a supplement to the online version of this article at http://www.ajph.org.

Data

We used data from the National Center for Health Statistics (NCHS) Linked Birth/Infant Death Cohort Files for all available years from 1983 to 2004 (1992–1994 were unavailable from NCHS, and state identifiers were unavailable after 2004). These data matched the birth certificates from a calendar year to the death certificates for infants who died within the first year of their life. We restricted our analysis to births that occurred in the 50 states and the District of Columbia to mothers who identified themselves as Black or White.

We defined risk factors to include covariates that were frequently used in previous studies and that were likely to be determined before the mother could receive information about the health of the fetus. Although associations between mortality and such covariates do not necessarily represent causal relationships, restricting ourselves to such predetermined covariates eliminates the possibility of reverse causality. The risk factors we included were maternal education (indicators for 5 categories), age (indicators for 6 categories), marital status, previous pregnancy loss (indicator for either elective or spontaneous loss), whether any prenatal care was received in the first 3 months of the pregnancy, infant gender, live birth order (indicators for 5 categories), and plurality. In addition, we included indicators for the state in which a birth occurred (the 50 states and the District of Columbia). The state indicators are potentially useful additions because state-level variation in many important inputs for producing healthy infants, such as employment opportunities and social assistance generosity, might be correlated with state-level variation in race. In defining these risk factors, we were limited to information publicly available from birth certificates, which did not include many factors that are hypothesized to affect IMR, including detailed socioeconomic characteristics, maternal stress, and environmental factors.

Our goal of examining IMR changes over a long time faced the additional challenge that the available data changed over time. To obtain a data series that included the desired risk factors and most states over the entire time period, we included Hispanic Blacks and Whites, excluded 4 states with substantially incomplete education information in some of the relevant years (California, New York, Texas, and Washington), and dropped observations for whom any of the risk factors were missing. We refer to this data series as our analytic series. We also produced some select results for all available Whites and Blacks, which we refer to as the full series.

Our outcomes of interest were the absolute IMR gap, measured as the difference in deaths in the first year per 1000 live births, and 2 of its commonly analyzed components, a birth weight component and an IMR conditional on birth weight component. Although previous studies examined both absolute and relative gaps,¹⁵ we examined the absolute IMR gap because it allowed us to separately study trends in the explained and unexplained gaps. We used birth weight as our measure of health at birth in our baseline analysis because it was measured more accurately than gestational age and was missing less frequently, especially in the early years. However, several studies suggested that gestational age was likely a better measure of health at birth, so we also performed all analyses using gestational age^2,16 (see the section on Sensitivity Analysis).

Analytical Strategy

To examine how the IMR gap and its components were related to the previously described 9 risk factors, we used inverse probability weighting (IPW) methods.^17,18 Our IPW methods were a form of direct standardization: we constructed “counterfactual” quantities by weighting groups to have the same distribution of risk factors. Counterfactual quantities could be compared with actual quantities to assess whether the risk factors could explain group differences in an outcome. The benefit of using IPW methods rather than regression-based methods (like Oaxaca-Blinder decompositions) was that IPW methods allowed us to examine differences in quantities other than means, such as differences in the cumulative distribution of deaths across birth weight.

To construct these counterfactual quantities, note that an outcome y for a group can be expressed as function of the group’s distribution of risk factors X and the group’s relationship between the outcome y and the risk factors X. For example, letting 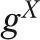denote the group whose distribution of risk factors X is being used, 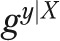denote the group whose relationship between the outcome y and risk factors X is being used, and 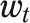denote Whites at time t, then the actual outcome y for Whites at time t is 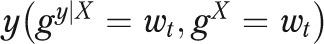. Turning to a counterfactual quantity, the outcome y that would exist if Whites had the distribution of risk factors of Blacks at time τ (where τ may or may not equal t), while retaining their own relationship between X and y at time t, can be written as 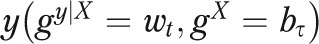. The insight of inverse probability weighting methods is that such counterfactual quantities can be easily recovered by reweighting the White population at t to have the risk factors of Blacks at time τ.^18,19

Counterfactual quantities constructed in this way can then be used to assess how much of a Black–White gap in an outcome can be explained by the risk factors. For example, letting 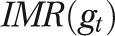be the actual IMR for group g at time t, the Black–White IMR gap is 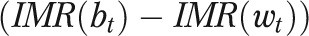. In addition, denote the IMR in the White population weighted to have the Black distribution of risk factors, both in year t, as

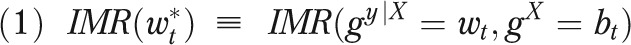Then, the part of the IMR gap that is explained by the risk factors X is 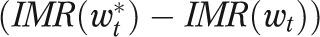and the unexplained part is 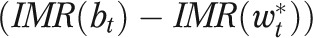. Furthermore, rewriting the explained gap as

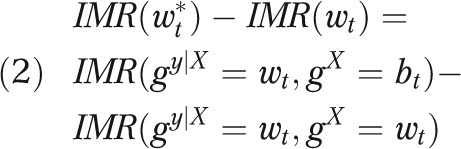illustrates that year-to-year changes in the explained gap can arise from changes in the risk factors within either group (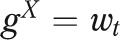 or 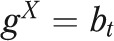) or from changes in the relationship between risk factors and IMR among Whites 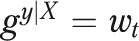. We note that we could have defined the explained gap by weighting Blacks to have the distribution of risk factors found among Whites; we explored this issue further with sensitivity analysis.

To better understand the unexplained and explained gaps, we examined how they emerged over the birth weight distribution. Specifically, we partitioned births into 173 mutually exclusive birth weight categories, corresponding to integer ounce values of birth weight and 1 category for missing birth weight. For both groups, we calculated the number of deaths in each category per 1000 total live births (across all birth weight categories), and then cumulated the differences in deaths between Blacks and Whites over the birth weight distribution. We constructed these cumulative gap curves for the actual, unexplained, and explained IMR gaps.

We also decomposed the unexplained IMR gap into a birth weight component and a conditional IMR component.^6,7,18,20 Letting 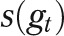represent a 173 × 1 vector of the shares of births in the respective categories and 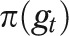represent a 173 × 1 vector of birth weight-specific mortality rates for the same categories, both for group 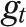, we decomposed the unexplained IMR gap at time t as

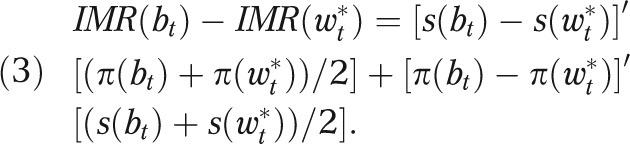The first term on the right-hand side of the previous equation is the component of the unexplained IMR gap attributed to differences in the birth weight distributions 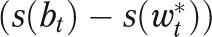, and the second term is the component attributed to differences in the birth weight-specific mortality rates 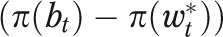. For these analyses that examined IMR gaps across the birth weight distribution, we used data for four 2-year periods (1983–1984, 1989–1990, 1996–1997, and 2003–2004). We also dropped observations with missing birth weight, which reduced the gaps a little, especially in the early periods.

We assessed the precision of our results by using a simple bootstrap. We tested hypotheses by using the bootstrapped standard errors to compute the 2-tailed t-test.

Further details on the data and methods are provided as a supplement to the online version of this article at http://www.ajph.org.

RESULTS

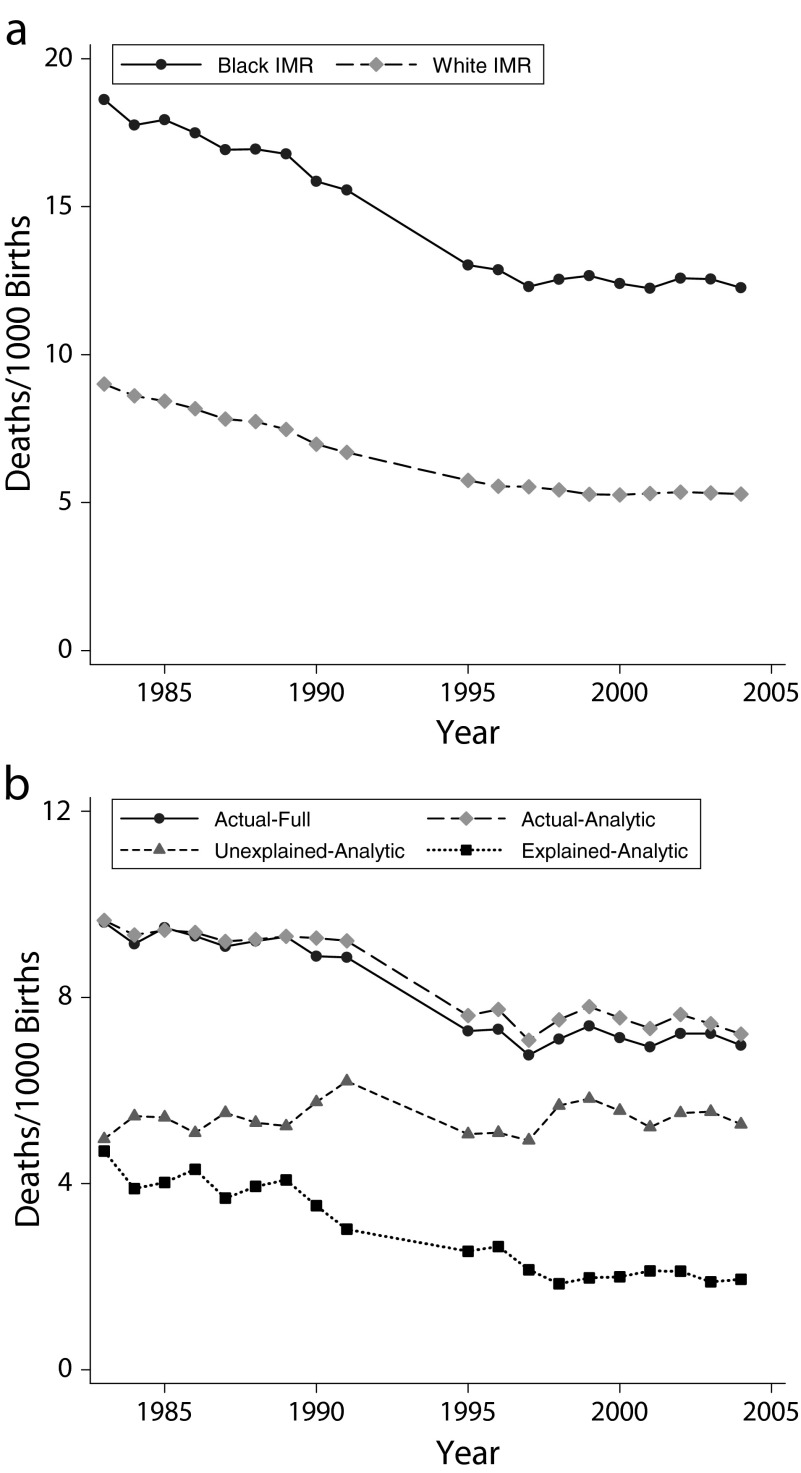
We began by tabulating the IMR among Blacks and Whites for the available years between 1983 and 2004 using the full series (Figure 1a). The IMR declined substantially over time, with the Black IMR declining by 6.3 (from 18.6 to 12.3) and the White IMR declining by 3.7 (from 9.0 to 5.3). We also plotted the absolute Black–White IMR gap based on the full series (Figure 1b), which declined by 2.6 (from 9.6 to 7.0). The rest of our analysis used the analytic series, which was constructed to have a common set of covariates available for each year. The IMR gap for the analytic series changed similarly to the IMR gap from the full series (Figure 1b), declining by a statistically significant 2.5 (from 9.7 to 7.2; P < .001).

FIGURE 1—

Trends in (a) IMR by race, full series, and (b) IMR gaps, full and analytic series: United States, 1983–2004.

Note. IMR = infant mortality rate. The full series refers to the entire sample of Blacks and Whites and the analytic series makes additional restrictions so that the covariates are defined consistently over time.

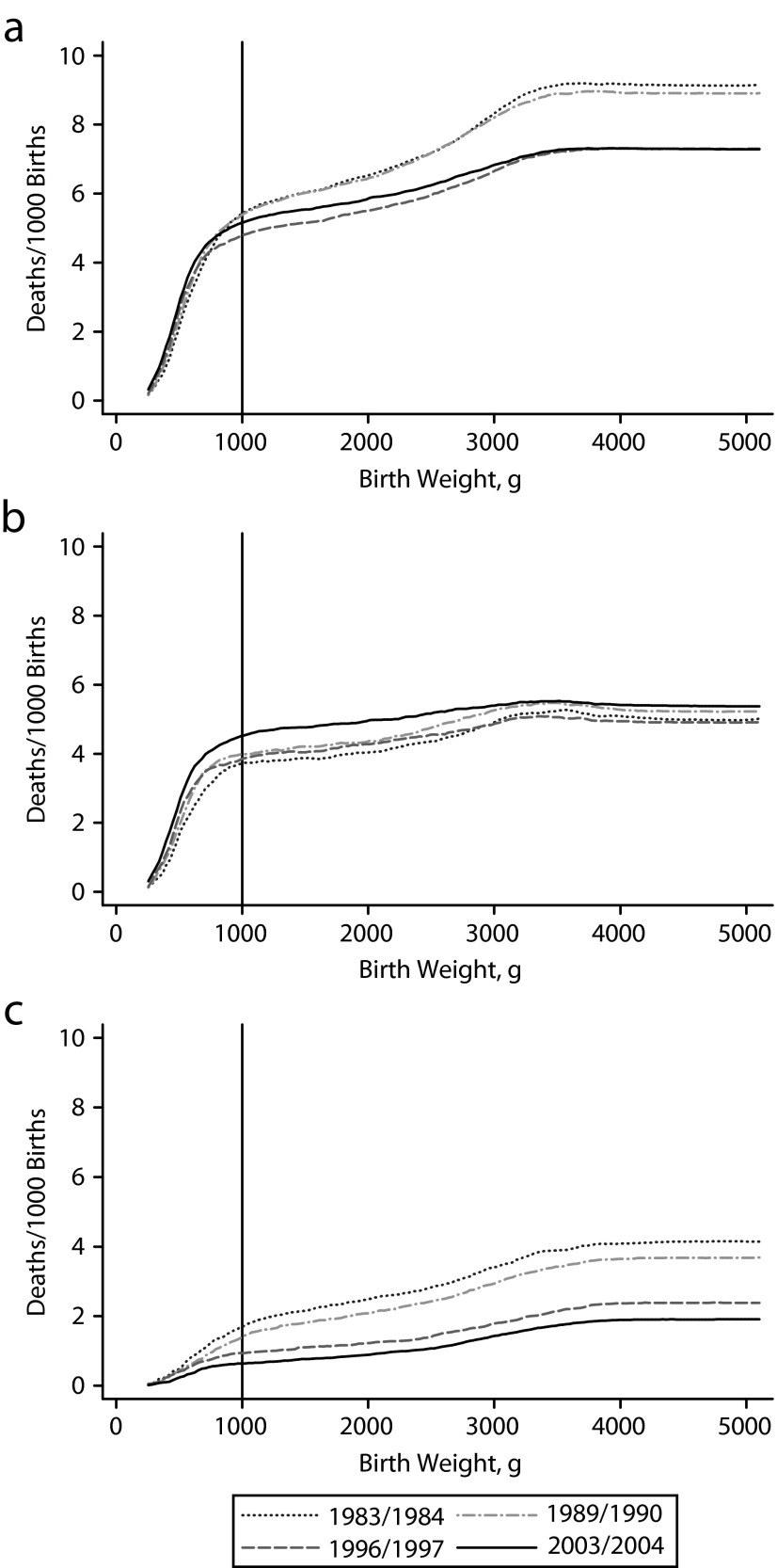
To probe how the IMR gap changed over time, we examined how it cumulated over the birth weight distribution. For example, consider the 1983–1984 curve for the actual IMR gap (Figure 2a). The height of the curve at its right-most endpoint is 9.2, representing the total IMR gap, and the height at 1000 grams is 5.4, implying that roughly 60% (5.4/9.2) of the total IMR gap was accounted for by infants weighing less than 1000 grams.

FIGURE 2—

Changes over time in (a) cumulative IMR gaps, (b) unexplained cumulative IMR gaps, and (c) explained cumulative IMR gaps: United States, 1983–2004.

Note. IMR = infant mortality rate. The analytic series was used to construct these graphs.

Comparing the different cumulative curves for the actual IMR gaps, we found that a large, relatively similar IMR gap emerged at less than 1000 grams in all 4 time periods, whereas the IMR gaps diverged much more at weights more than 1000 grams (Figure 2a). For example, comparing 1983–1984 to 2003–2004, the total gap declined by 1.9 deaths per 1000 live births (9.2 vs 7.3). Between these same 2 periods, the decline in the IMR gap that occurred at less than 1000 grams was only 0.2 deaths per 1000 live births (5.4 vs 5.2), roughly 10% of the total decline (0.2/1.9). In other words, much of the IMR gap emerged at less than 1000 grams in all time periods, but little of the change in the IMR gap occurred at these very low birth weights.

Unexplained Gap

We then examined how the unexplained IMR gap, the part of the gap that was left after we adjusted for differences in risk factors, changed over time (Figure 1b). The unexplained gap was remarkably stable over these 2 decades, changing from 5.0 in 1983 to 5.3 in 2004. In all years but one (1991), the unexplained gap remained within 2 standard errors (2 × 0.4) of the 1983 estimate.

To probe how the unexplained IMR gap changed over time, we examined how it cumulated over the birth weight distribution. The cumulative curves for the unexplained IMR gaps (Figure 2b) revealed less change over the 2-decade period compared with the actual IMR gaps (Figure 2a), both in their level and how they accumulated over the birth weight distribution. For example, between 1983–1984 and 2003–2004, the change in the overall unexplained IMR gap was only 0.4 (an increase from 5.0 to 5.4; P = .201). However, the curves revealed that the unexplained gap became more concentrated at less than 1000 grams. For example, the change in the unexplained gap that existed at less than 1000 grams was 0.8 (from 3.7 to 4.5; P < .001).

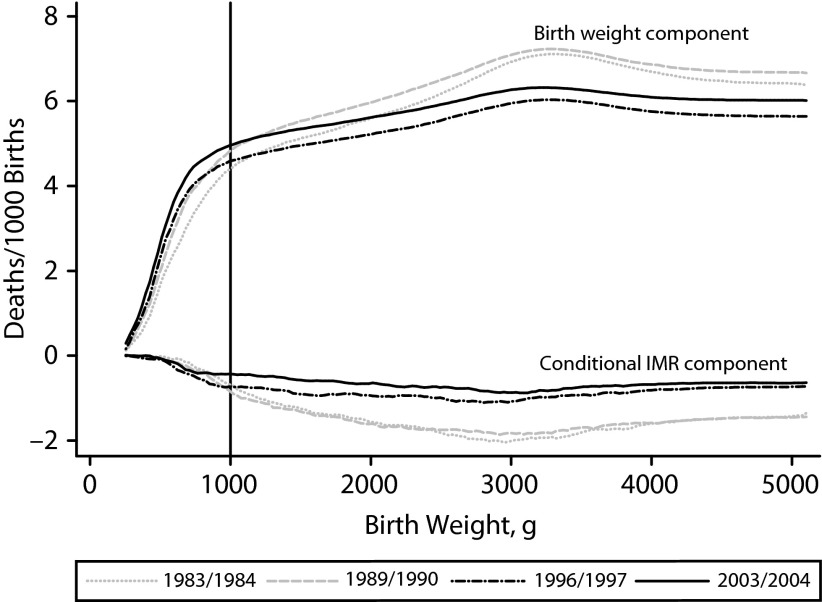
Although the cumulative unexplained IMR gap curve showed where in the birth weight distribution the differences between Blacks and Whites arose, it did not tell us whether the differences were attributed to differences in birth weight distributions or in IMR conditional on birth weight. To investigate further, we decomposed the unexplained IMR gap into its birth weight and IMR components following equation 3, again focusing on four 2-year periods and showing how these components accumulated across the birth weight distribution (Figure 3). The conditional IMR component was negative in each period, implying that the birth weight component more than fully accounted for the entire unexplained IMR gap. Moreover, this birth weight component largely emerged at less than 1000 grams in each period. Thus, the unexplained part of the IMR gap was very stable over 2 decades and was almost entirely attributable to differences in the birth weight distribution between Blacks and Whites at less than 1000 grams.

FIGURE 3—

Cumulative components of the unexplained IMR gap: United States, 1983–2004.

Note. IMR = infant mortality rate. The analytic series was used to construct these graphs.

Explained Gap

As expected, given the decline in the actual IMR gap and the stability of the unexplained IMR gap, we found that the explained IMR gap declined over our sample period (Figure 1b). The explained gap declined by a statistically significant 2.8 between 1983 and 2004 (from 4.7 to 1.9; P < .001). Moreover, we found that much of the explained IMR gap emerged at more than 1000 grams, especially in the initial years (Figure 2c). Taken together, these comparisons suggested that much of the gap that occurred at less than 1000 grams was unexplainable based on risk factors in all years, whereas the decline in the IMR gap that occurred at more than 1000 grams was largely explainable.

We then sought to understand why the IMR gap became less explainable. This decline could stem from either a Black–White convergence in risk factors or changes in the relationship between risk factors and mortality. For example, consider the risk factor single motherhood. In 1983, there was a sizeable gap in IMR between single and married mothers among Whites (an IMR gap of 5.9 in the raw data, but a sizeable IMR gap would remain if it were adjusted for differences in the other risk factors¹⁸), and single births were more prevalent among Black mothers than White mothers (the share of births to single mothers was 0.48 higher for Blacks than for Whites). Taken together, these differences implied that single motherhood explained some of the IMR gap in 1983. If the IMR gap between single and married White mothers declined (which it did, to 3.1 in 2004) or if the difference in the prevalence of single births between Whites and Blacks declined (which it did, to 0.41 in 2004), then the explained IMR gap would decline.

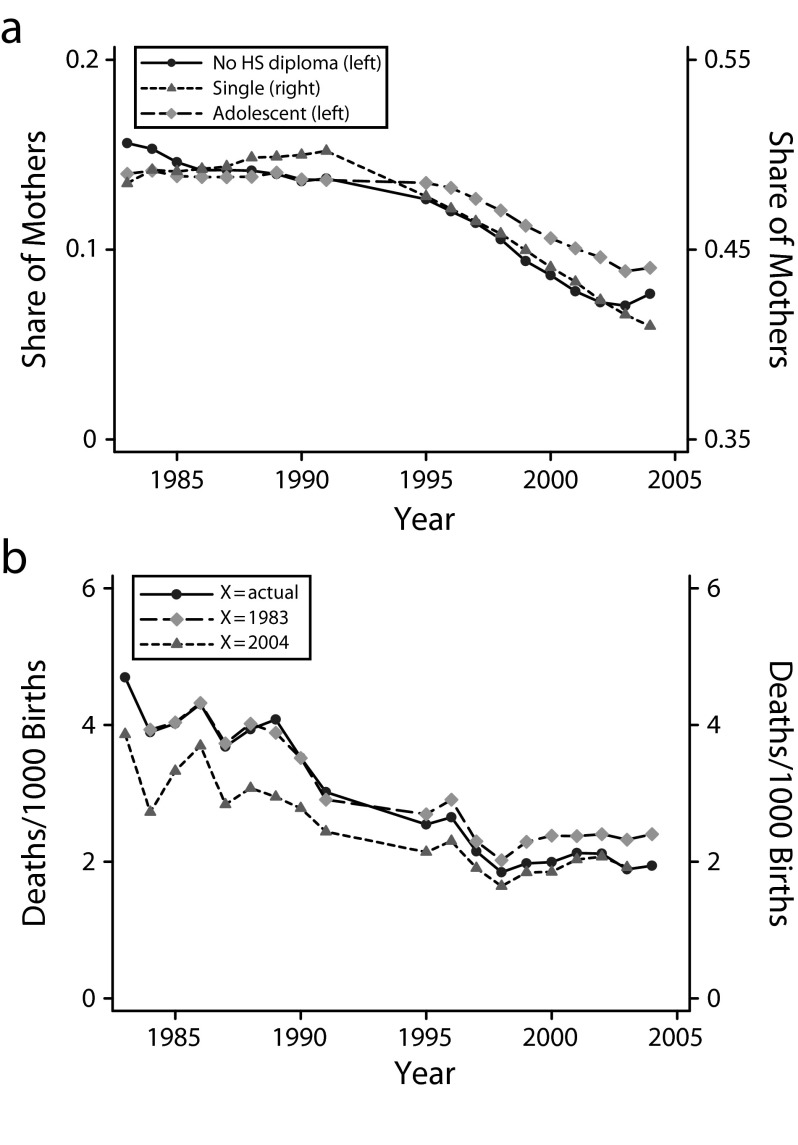
We first examined changes in selected risk factors (Figure 4a). The gaps between Black and White mothers declined along 3 important dimensions: single motherhood, adolescent motherhood, and noncompletion of high school. However, the timing of these declines did not coincide with the decline in the IMR gap. Specifically, we found that much of the convergence in IMR took place before 1995 (Figure 1b), whereas the convergence in these risk factors mainly took place after 1995 (Figure 4a).

FIGURE 4—

Trends in (a) gaps in maternal risk factors and (b) explained IMR gaps: United States, 1983–2004.

Note. HS = high school; IMR = infant mortality rate. The analytic series was used to construct these graphs. In part a, the legend lists the y-axis used for each characteristic (e.g., left or right). In part b, the legend lists the risk factors used in computing each explained IMR gap (e.g., the risk factors from the actual year, 1983, or 2004).

We then directly examined the changes in the relationship between risk factors and mortality. We first computed the actual decline in the explained IMR gap in each year (Figure 4b). The 2.8 decline between 1983 and 2004 (from 4.7 to 1.9) was slightly larger than the 2.7 decline in the overall IMR gap (from 9.7 to 7.2). We then computed the decline in the explained IMR gap that would have occurred if we held the distributions of Black and White risk factors constant at their 1983 levels, while allowing the relationship between risk factors and IMR to change (in Figure 4b). Roughly 80% of the decline ([4.7–2.4]/[4.7–1.9] × 100) occurred even when risk factors were held constant. To verify that the finding was not specific to using the 1983 distributions of risk factors, we repeated the exercise using the 2004 distributions (Figure 4b) and found similar results: most of the explained IMR gap decline was evident even when risk factor distributions were held constant. Therefore, most of the decline in the explained IMR gap must have arisen because the risk factors became less predictive of IMR over time.

Sensitivity Analyses

We performed several analyses to examine whether our findings were specific to the analytical choices we made. In one, we computed explained gaps by weighting Blacks to match the risk factors found among Whites, rather than weighting Whites to match the risk factors found among Blacks. Another included only singletons and first births, rather than including all births and including plurality and birth order as risk factors. Another excluded Hispanics to follow many previous studies, which necessitated dropping several states and all years before 1989. Lastly, we used gestational age as our measure of infant health rather than birth weight. For all of these alternative analyses, the results were similar to those reported in the text and are included as a supplement to the online version of this article at http://www.ajph.org.

DISCUSSION

We documented that, despite declines in the actual IMR gap from 1983 to 2004, the unexplained IMR gap was remarkably stable in its size and its relationship to birth weight and gestational age over this time. Although previous studies examined the relationship of the IMR gap to health at birth or examined the relationship of the IMR gap to background factors, no previous study examined trends in the relationship between IMR and health at birth after adjusting for changing risk factors.

Because the actual IMR gap declined while the unexplained gap remained stable, the explained gap also declined over our sample period. This decline was mostly related to a declining association between risk factors and infant death, rather than related to a convergence of risk factors between Blacks and Whites. One interpretation of this finding was that advances in medical care rendered individual and institutional behaviors related to these risk factors less important for infants’ survival.

Another contribution of our study was the treatment of geography. Many inputs for producing healthy infants vary by state, including employment opportunities, social services, pollution, and access to health care, and the populations of Blacks and Whites are distributed quite differently across states.¹⁴ We included state indicators, allowing these indicators to affect mortality differently by year. This flexible specification incorporated all of the explanatory power that could come from any risk factor that varied only at the state and year level, such as state-level Medicaid policy or social assistance variables. Nonetheless, the explained gap was only a small share of the total gap by the end of our sample period.

One interpretation of our results was that there existed a set of unspecified factors that were central to the IMR gap, that changed very little over the 20-year period we considered, and that were unrelated to the risk factors we controlled for. We posit that these unspecified factors were unrelated to the risk factors we included for 2 reasons. First, the stable, unexplained gap was concentrated among births at less than 1000 grams, whereas the declining explained gap was concentrated among births at more than 1000 grams. Second, the stark contrast in the trends between the explained gap and unexplained gap suggested they are unrelated. It seems unlikely that the unexplained gap would have remained so stable over the 2 decades if it were mainly composed of unobserved risk factors that were closely related to the observed risk factors. Thus, the observed risk factors associated with the declining explained gap appears to be distinct from those unobserved factors associated with the stable unexplained gap. Moreover, the search for these unobserved factors should be focused on those that lead to low birth weights and for preterm births.

The fact that the unexplained and explained gaps appear to be so distinct has important implications for the various hypotheses that have been put forward for why the gap exists. As an illustration, consider Black–White differences in socioeconomic status. Our observed risk factors included mother’s education, age, and marital status, but they did not include income and wealth and neighborhood quality, implying that any Black–White gaps in these latter factors (after controlling for our observed risk factors) were left in the unexplained gap. It seems unlikely that the unexplained gap would be so distinct if it were mainly composed of unobserved factors that were closely related to the observed risk factors. Thus, this unexplained gap is unlikely to be primarily composed of factors related to unmeasured socioeconomic status or other unobserved factors strongly correlated with the risk factors we observed.

Limitations

We note 2 important caveats to our analysis. First, it is important to recognize that associations between outcomes and the predetermined risk factors that we used here are only a starting point for understanding the causal mechanisms at work. For example, we followed many other studies of infant mortality in including a measure of prenatal care, but numerous authors questioned whether the measured association between mortality and prenatal care represent a causal effect.^21,22 Second, despite our additional inclusion of state indicators, the set of risk factors available in Vital Statistics data were limited.

Conclusions

We studied the 1983 to 2004 trend in a striking and fundamental disparity in the United States: the differential rate at which White and Black infants die. Although the Black–White IMR gap declined over this period, the unexplained IMR gap was remarkably stable in its size and its relationship to birth weight. By 2004, this unexplained gap constituted most of the overall IMR gap and was concentrated among infants with birth weights at less than 1000 grams, who were almost always born prematurely and had high mortality rates. In addition, the IMR gap declined primarily because our observed risk factors became less predictive of infant mortality. In terms of future progress for reducing this IMR disparity, our findings are somewhat discouraging because, if the unexplained IMR gap continues its 2 decades of stability, even the complete elimination of the explained gap would reduce the Black–White IMR gap by only one quarter. In terms of future progress for understanding this IMR gap, our findings were more constructive because they imply that one should look to risk factors that are distinct from those commonly derived from birth certificate data and that influenced the share of births at which the infants weighed less than 1000 grams.