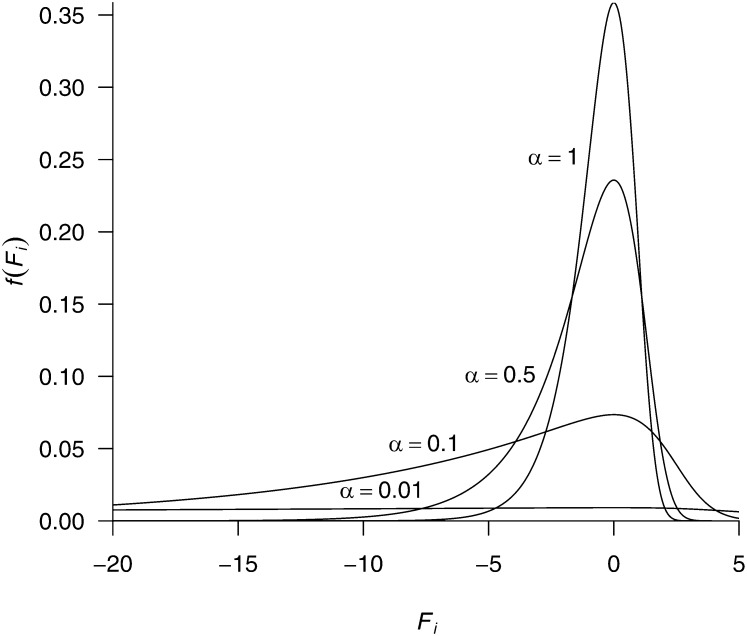
Figure 1.
Marginal distribution density of Fi when θ = (θi) ∼ Dirichlet(θ | α). The marginal density of θi is f(θi) = Beta(θi | α, αk − α), and the marginal density of Fi is f(Fi) = f(θi) × J = Beta(θi | α, αk − α) × θi(1 − θi), with θi = exp Fi/(k − 1 + exp Fi). A Dirichlet distribution with α = 1 is very informative on the transformed parameter space on F: The 95% equal-tail range of θi is (0.00133, 0.176), corresponding to a 95% range for Fi of (−3.68, 1.41).