Choosing profile double-sampling designs for survival estimation with application to PEPFAR evaluation

Abstract

Most studies that follow subjects over time are challenged by having some subjects who dropout. Double-sampling is a design that selects, and devotes resources to intensively pursue and find a subset of these dropouts; then uses data obtained from these to adjust naïve estimates, which are potentially biased by the dropout. Existing methods to estimate survival from double-sampling assume a random sample. In limited-resource settings however, generating accurate estimates using a minimum of resources is important. We propose using double-sampling designs that oversample certain profiles of dropouts as more efficient alternatives to random designs. First, we develop a framework to estimate the survival function under these profile double-sampling designs. We then derive the precision of these designs as a function of the rule for selecting different profiles, in order to identify more efficient designs. We illustrate using data from a United States President’s Emergency Plan for AIDS Relief (PEPFAR)-funded HIV care and treatment program in western Kenya. Our results show why and how more efficient designs should oversample patients with shorter dropout times. Further, our work suggests generalizable practice for more efficient double-sampling designs, which can help maximize efficiency in resource-limited settings.

1 Introduction

In most studies that follow subjects over time, some subjects discontinue their contact with the investigators (also called patient dropout). Double-sampling is a design that selects a subset of the dropouts and devotes enough resources to intensively pursue and find their information. When survival is the target of estimation, the methods that are needed to analyze the double-sampled data are different and more demanding than those for simpler designs; see, for example, Frangakis and Rubin [1], Baker, Wax, and Patterson [2], and An et al. [3]. Most such designs so far assume that the double-sampled subset is a random sample of all the dropouts.

In most settings, maintaining high precision of the estimates for low cost is a serious concern. For example, the United States President’s Emergency Plan for AIDS Relief (PEPFAR, www.pepfar.gov), an international response effort initiated in 2003 with a $15 billion budget and renewed in 2008 for five additional years with a $48 billion budget, works in part to provide antiretroviral therapy (ART) to HIV-infected individuals in resource-poor countries, primarily in sub-Saharan Africa. Key goals of this effort include increasing access to treatment, and ultimately improving survival of HIV-infected patients under care provided by its partners. Congress mandates, as part of the PEPFAR funding, monitoring and evaluation of the funded programs. Therefore it is important, in order to monitor the program, that methods of evaluating survival optimize precision subject to cost and sampling constraints. A natural question then is, instead of double-sampling at random, can we oversample certain profiles of individuals in order to gain efficiency?

There are several reasons why double-sampling based on patient characteristics is important for gaining efficiency. First, it is well-known that patient characteristics (e.g., CD4 count) can predict survival time in HIV patients [4, 5]. Second, imagine oversampling individuals who have been under observation for a short period (i.e., they have short dropout times). These individuals expectedly provide more information towards the target estimand, beyond what we would have without double-sampling them, relative to individuals with long dropout times. With the latter group, it is more likely they have passed the time for which survival estimates are of interest. We refer to this selective double-sampling as “profile” double-sampling.

We develop a framework that characterizes the role of different such profile double-sampling designs for inference on survival data. Using this framework, we obtain insightful expressions of precision as functions of the design. By studying classes of double-sampling designs, we obtain profile designs that have improved precision and suggest generalizable practice.

In Section 2, we briefly describe the circumstances motivating this work and review the double-sampling design for survival data. In Section 3, first, we develop a likelihood framework that allows survival estimation from a double-sample based on individual information, and focus on a maximum-likelihood based approach. In Section 4, we derive the precision of the maximum likelihood estimator (MLE) for a given profile double-sampling design, which allows comparison of different double-sampling designs. In Section 5, we apply our methods in the evaluation of a large HIV care and treatment program in western Kenya, and identify a profile double-sampling design that is considerably more efficient than simple or ad hoc random double-sampling designs. Section 6 concludes with a discussion.

2 Profile Double-Sampling Design and Goal

The design is motivated by data assembled for a cohort of 8,977 HIV-infected adults who entered the Academic Model Providing Access to Healthcare (AMPATH), a comprehensive HIV care and treatment program located in western Kenya, between January 1, 2005 and January 31, 2007. The goal here is to estimate the survival distribution of these individuals after their enrollment in the program, P(T > t). The care and treatment program and the patient double-sampling (“outreach”) efforts are described in detail elsewhere [3, 6–8]. For our purpose we can summarize these by viewing the design as having two phases.

In Phase 1 of the design, monitoring proceeds with standard effort (i.e., no double-sampling). Here, we observe the entry date E_i for all patients. If standard monitoring continued indefinitely, we would observe that some patients discontinue contact from the standard monitoring: we call these patients true dropouts and indicate them by R_i = 0, and denote their time from enrollment (i.e., time 0) to dropout by L_i. On the other hand, some patients would be true non-dropouts, whom we indicate by R_i = 1 and for whom L_i is undefined. Further, patients may be subject to administrative censoring. That is, if the time of analysis is “Now” (E_max), then the time between enrollment E_i and E_max is known as the administrative censoring time, and denoted by C_i. Patients who have C_i < T_i are administratively censored and are indexed by Δ_i = 0; otherwise patients are indexed by Δ_i = 1. It is important to note that administrative censoring allows only a subset of the true dropouts (R_i = 0) to be observed and known as true dropouts, whereas for the others, their true dropout status (that they would dropout later) is masked by administrative censoring. A person observed to dropout is denoted by $R_i^{\mathit{obs}}=0$ and one observed to not dropout is denoted by $R_i^{\mathit{obs}}=1$, and could either have R_i = 0 or R_i = 1.

Double-sampling efforts introduce a second phase in the design. In Phase 2, investigators select a subset of the observed dropouts $(R_i^{\mathit{obs}}=0)$, called a double-sample, by using baseline characteristics Z_i and possibly dropout time L_i, and devote enough resources to follow this subset and find either their survival time or that they are alive until E_max, i.e., we find (X_i ≡ min(T_i, C_i), Δ_i). We indicate by D_i = 1 those who are double-sampled, and D_i = 0 otherwise. Expressed statistically, this Phase 2 design structure adds the following important condition:

Condition 1: Designed Profile Double-Sampling

Among observed dropouts, the observed covariates Z_i and dropout time L_i include the variables involved in the selection and successful recovery of those to be double-sampled. We can express this by stating that, among observed dropouts and after we condition on Profile_i = (Z_i, L_i), selection for and recovery by double-sampling is independent of survival and entry times, or equivalently,

$$D_i\perp (T_i,C_i)\mid (R_i^{\mathit{obs}}=0,{\text{Profile}}_i),\text{since entry times}{E}_i=E_{\mathit{max}}-C_i.$$

Note that L_i is measured after entry time, but can be an important factor for precision of the design as discussed in the introduction. Because the typical survival data (X_i, Δ_i) are functions of (T_i C_i), it is an immediate implication of Condition 1 that, conditional on the observed covariates, selection for and recovery by double-sampling is independent of (X_i, Δ_i): D_i ⊥ (X_i, Δ_i) ∣ ($R_i^{\mathit{obs}}=0$, Profile_i).

Based on the above, the choices the investigator has for a particular profile double-sampling design are the time of analysis E_max, and the rule for double-sampling given dropout and individual characteristics,

$$e\left({\text{Profile}}_i\right)=P(D_i=1\mid R_i^{\mathit{obs}}=0,{\text{Profile}}_i).$$ (1)

For a given pattern of entry dates, E_max determines the distribution of administrative censoring times, P(C∣Z). We consider the time of analysis (E_max) fixed and search for best designs of the form described in equation (1).

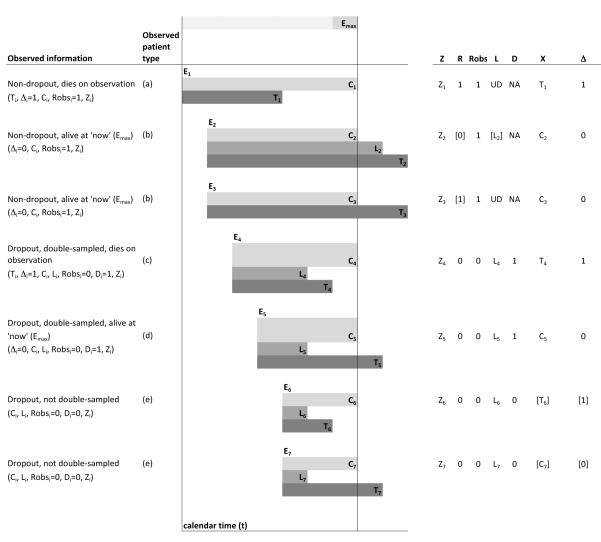
Information from these phases can be classified into patient characteristics (i.e., E_i, T_i, R_i, L_i, Z_i; Figure 1), design characteristics (E_max, D_i, Profile_i; Figure 1), and a product of both patient and design characteristics (C_i, $R_i^{\mathit{obs}}$, X_i, Δ_i; Figure 1); and can be used to estimate the cohort survivor function P(T > t).

Figure 1.

Characteristics for different patient types. The observed patient type labels correspond to those in the likelihood, described in Section 3. Data in square brackets[ ] are only partially observed; “UD” means undefined and “NA” means not available or missing.

Note that R_i and $R_i^{\mathit{obs}}$ can be different. R_i is a characteristic of the patient, and both R_i and L_i are missing if the person is administratively censored. On the other hand $R_i^{\mathit{obs}}$, although observed, is determined by both the patient characteristics R_i and L_i and by the design’s time of analysis E_max, namely whether L_i < E_max–E_i. Thus the concept of true dropout behaviour, R_i and L_i, is central for separating patient from design characteristics.

For estimability, since T is still missing for the administratively censored patients, we invoke the following condition:

Condition 2: Time homogeneity

Conditional on the observed covariates, entry time (equivalently, administrative censoring time) is independent of survival time and of potential dropout status. We can express this as: C_i ⊥ (T_i, R_i, L_i) ∣ Z_i, since entry times E_i = E_max–C_i.

We note that Condition 2 includes the typical conditional independence of administrative censoring, C_i ⊥ T_i ∣ Z_i. Moreover, Condition 2 is plausible within blocks of time if, conditional on observed covariates such as gender, baseline CD4 count, baseline World Health Organization (WHO) stage, clinic type, and treatment status, we assume no secular trends in survival or true dropout behavior. Such an assumption could not be expressed in terms of observed dropout status, which depends not only on patient characteristics but also on design characteristics such as the time of analysis (E_max).

3 Estimation for a given design

A useful intuition for how appropriate estimation can work and for what can go wrong with a standard approach is provided from the simple case where double-sampling does not depend on patient data other than that a patient has been an observed dropout. Then, the “typical survival information”, (X_i, Δ_i), is missing at random [9] within the stratum of observed dropouts (R^obs = 0). In that case, for the double-sampled individuals, for whom the data (X_i, Δ_i) are recovered, the only remaining source of missing survival times is the possible administrative censoring by C_i. Under Conditions 1 and 2 with no covariates, a consistent nonparametric estimator can then be constructed by, in principle, scaling up the distribution of (X_i, Δ_i) from the double-sampled patients to the set of all dropout patients. This scaling up in practice is achieved by mixing estimates of the two crude hazard functions of observed non-dropouts and double-sampled dropouts [1]. In contrast, a standard approach that would mix the two Kaplan-Meier estimators based on those two strata is in general inconsistent even if there is no covariate necessary to stratify in Conditions 1 and 2. This is because the strata of observed dropouts/non-dropouts are functions not only of the inherent patient characteristic (R_i, L_i, T_i) but also of the design characteristics (Section 2). This creates a dependence between administrative censoring C_i and survival T_i within the observed strata R^obs even under Conditions 1 and 2, and so invalidates the within-strata Kaplan-Meier estimators. Analogous arguments hold if we use a double-sampling design that depends on discrete levels of baseline covariates, where a consistent nonparametric MLE from simple data still exists [3].

When the design depends on a multitude of data or continuous patient history data, a nonparametric MLE is not possible. In this case, one important task is to find and use the MLE of a plausible parametric model. Alternatively, one can find estimators that use the inverse of the double-sampling probabilities and are based on a semi-parametric framework, e.g., [10]. The latter approach also requires the use of likelihood estimators because (a) the augmentation part needed to construct locally efficient semi-parametric estimators is itself derived from a general likelihood submodel [11]; and (b) the approach of inverting probabilities does not work for designs that exclude from the double-sampling certain patients who are practically impossible to find. Therefore, for all the above approaches, it is central to first find the likelihood of data from designs under Conditions 1-2. So we present the discussion on design efficiency from a likelihood perspective. Perspectives based on a semi-parametric approach will be studied in future work.

The target estimand, the survivor function, can be expressed through the chain of conditional distributions (here T, R, Z, L represent the random variables corresponding to their respective individual counterparts T_i, R_i, Z_i, L_i):

$$\begin{array}{cc}\hfill P(T>t\mid Z,\theta )=& P(T>t\mid Z,R=1,\theta )P(R=1\mid Z,\theta )+\hfill \\ \hfill & {\int }_{l\ast \ast \ast t}P(T>t\mid Z,R=0,L=l,\theta )P(L=l\mid Z,R=0,\theta )P(R=0\mid Z,\theta )dl\hfill \end{array}$$

When S(t ∣ Z, θ) := P(T > t ∣ Z, θ) is estimated by $S(t\mid Z,\widehat{\theta })$, we can estimate the cohort (marginal) survivor function S(t ∣ θ) in our original goal as a function of t, by the empirical average over all n individuals:

$$\widehat{S}\left(t\right)=\tilde{S}(t\mid \widehat{\theta })=\frac{1}{n}\sum _{i=1}^{n}S(t\mid Z_i,\widehat{\theta })$$ (2)

In order to estimate S(t ∣ Z, θ), it is important to find how the likelihood depends on arbitrary (nonparametric) distributions of the observed data. To write the likelihood of the observed data in Section 2, which we denote collectively by Data_i for each person, first note that the covariates Z_i and administrative censoring time C_i are observed for all people. Then, it is useful to classify the patients into the following five types described below and displayed in Figure 1:

1. a non-dropout who dies on observation ($R_i^{\mathit{obs}}=1$, Δ_i = 1), for whom we also observe survival time T_i and for whom L_i is undefined;

2. a non-dropout alive at time of analysis ($R_i^{\mathit{obs}}=1$, Δ_i = 0), for whom L_i is either undefined or missing according to whether they are true non-dropouts or true dropouts, respectively;

3. a dropout who is double-sampled and dies on observation ($R_i^{\mathit{obs}}=0$, D_i = 1, Δ_i = 1), for whom we also observe the dropout and survival times L_i, T_i;

4. a dropout who is double-sampled and is alive at the time of analysis ($R_i^{\mathit{obs}}=0$, D_i = 1, Δ_i = 0), for whom we also observe dropout time L_i; or

5. a dropout who is not double-sampled ($R_i^{\mathit{obs}}=0$, D_i = 0), for whom we also observe dropout time L_i.

It follows from the above that, if we let θ denote the vector of parameters, the observed likelihood for an individual is given by:

$$P({\text{Data}}_i\mid Z_i,\theta )=P{(T_i,{\Delta }_i=1,C_i,R_i^{\mathit{obs}}=1\mid Z_i,\theta )}^{R_i^{\mathit{obs}}{\Delta }_i}$$ (3a)

$$\times P{({\Delta }_i=0,C_i,R_i^{\mathit{obs}}=1\mid Z_i,\theta )}^{R_i^{\mathit{obs}}(1-{\Delta }_i)}$$ (3b)

$$\times {\left\{P(T_i,{\Delta }_i=1,C_i,L_i,R_i^{\mathit{obs}}=0\mid D_i=1,Z_i,\theta )\cdot e\left({\text{Profile}}_i\right)\right\}}^{(1-R_i^{\mathit{obs}})D_i{\Delta }_i}$$ (3c)

$$\times {\left\{P({\Delta }_i=0,C_i,L_i,R_i^{\mathit{obs}}=0\mid D_i=1,Z_i,\theta )\cdot e\left({\text{Profile}}_i\right)\right\}}^{(1-R_i^{\mathit{obs}})D_i(1-{\Delta }_i)}$$ (3d)

$$\times {\left\{P(L_i,C_i,R_i^{\mathit{obs}}=0\mid D_i=0;Z_i,\theta )\cdot (1-e({\text{Profile}}_i\left)\right)\right\}}^{(1-R_i^{\mathit{obs}})(1-D_i)}$$ (3e)

where the lettering (a)-(e) corresponds to the types of patients described above and displayed in Figure 1. In the above expressions, we use, for example, P(T_i, Δ = 1, …) to mean P(T_i∣Δ_i = 1, …) · P(Δ_i = 1, …), i.e., the likelihood contribution of an individual i who is observed to die and whose survival is T_i and has other data …, which is the product of a density for T_i (given Δ_i = 1, …) and the likelihood of (Δ_i = 1, …).

The above expression is important for two purposes. First, it indicates how we can develop an E-M algorithm by capitalizing on the fact that (3b) is a mixture of terms for true dropouts (R = 1) and true non-dropouts (R = 0) (see supporting web files).Further, it is important for identifying a more efficient design, as shown in Sections 4 and 5. Notice that, once data are observed, the design components e() in (3c), (3d) and (3e) are ignorable [12] for likelihood estimation. These components are important, however, for estimating precision of candidate designs to be implemented on a larger scale, and thus will play a role in Sections 4 and 5.

4 The relation of precision to profile double-sampling designs

In order to facilitate the study of more efficient designs, it is useful to regroup the terms of the likelihood into two parts - the part that is contributed by all individuals from Phase 1, and the additional part that is contributed from the double-sampled individuals from Phase 2. We can do this by regrouping expression (2) as

$$\text{log}P({\text{Data}}_i\mid Z_i,\theta )={\ell }_{\text{phase}}^{\text{first}}({\text{Data}}_i;\theta )+D_i\cdot {\ell }_{\text{sample}}^{\text{first}}{\mid }_{\text{phase}}^{\text{first}}({\text{Data}}_i;\theta )$$ (4)

plus terms not depending on θ, where the above can be shown to be expressable in terms of the patient characteristics, as:

$$\begin{array}{cc}\hfill & {\ell }_{\text{phase}}^{\text{first}}({\text{Data}}_i;\theta )=R_i^{\mathit{obs}}{\Delta }_i\left\{\text{log}P\right(T_i\mid R_i=1,Z_i,\theta )+\text{log}P(R_i=1\mid Z_i,\theta \left)\right\}\hfill \\ \hfill & +R_i^{\mathit{obs}}(1-{\Delta }_i)\text{log}\left\{{\text{Surv}}_{T,R=1}\right(C_i,;Z_i,\theta \left)P\right(R_i=1\mid Z_i,\theta )+{\text{Surv}}_{L,R=0}(C_i;Z_i,\theta \left)P\right(R_i=0\mid Z_i,\theta \left)\right\}\hfill \\ \hfill & +(1-R_i^{\mathit{obs}})\text{log}P(L_i,R_i=0\mid Z_i,\theta )\hfill \end{array}$$ (5)

$$=(1-R_i^{\mathit{obs}})\left\{{\Delta }_i\text{log}P\right(T_i\mid R_i=0,{\text{Profile}}_i,\theta )+(1-{\Delta }_i\left){\text{log Surv}}_{T,R=0}\right(C_i;{\text{Profile}}_i,\theta \left)\right\},$$ (6)

The information matrix of the MLE of θ, defined as the expectation of the negative second derivative of (4), will depend on who is sampled, D_i = 1, only through the second term of (4), given in (6). From Section 2, “who is double-sampled” is characterized by the rule of selection e(Profile_i) where Profile_i = (Z_i, L_i), the variables used to select double-samples. So the expectation of the negative second derivative of (4) depends on the rule e(·) as well as θ, and is denoted by I(e(·), θ). It is easy to show (see supporting web files) the following useful results:

Result 1

The information of the MLE is related to the design e(·) by:

$$I\left(e\right(\cdot ),\theta )=I_{\text{Phase}}^{\text{first}}\left(\theta \right)+I_{\text{sample}}^{\text{dble}}{\mid }_{\text{phase}}^{\text{first}}\left(e\right(\cdot ),\theta )$$

where

$$\begin{array}{cc}\hfill I_{\text{phase}}^{\text{first}}\left(\theta \right)=& -E\left\{\frac{{\partial }^2}{\partial {\theta }^2}{\ell }_{\text{phase}}^{\text{first}}({\text{Data}}_i;\theta )\mid \theta \right\}\hfill \\ \hfill I_{\text{sample}}^{\text{dble}}{\mid }_{\text{phase}}^{\text{first}}\left(e\right(\cdot ),\theta )=& E\left\{e\right({\text{Profile}}_i\left)\delta \right({\text{Profile}}_i,\theta )\mid R_i^{\mathit{obs}}=0,\theta \}P(R_i^{\mathit{obs}}=0\mid \theta ),\hfill \end{array}$$ (7)

where $\delta ({\text{profile}}_i,\theta )=-E\{{\Delta }_i\frac{{\partial }^2}{\partial {\theta }^2}\text{log}P(T_i\mid R_i=0,{\text{Profile}}_i,\theta )\phantom{\}}$

$$\phantom{\{}+(1-{\Delta }_i)\frac{{\partial }^2}{\partial {\theta }^2}{\text{log Surv}}_{T,R=0}(C_i;{\text{Profile}}_i,\theta )\mid R^{\mathit{obs}}=0,{\text{Profile}}_i,\theta \phantom{\mid }\}$$

The design e(), through the above precision for θ, determines the precision for estimating the target estimand, the cohort survival curve S(t). In the supporting web files, we show the following:

Result 2

The large sample distribution of the estimator (2) is given by :

$$\sqrt{n}\left\{\frac{1}{n}\sum _{i=1}^{n}S(t\mid Z_i,\widehat{\theta })-S(t\mid \theta )\right\}\stackrel{d}{\to }N(0,V(e(\cdot ),\theta \left)\right),$$

where V(e(·), θ) = E_θ{S_θ(t ∣ θ)’} I(e(·), θ)⁻¹ E_θ{S_θ(t ∣ θ)} + var_θ{S(t ∣ Z_i, θ)} and S_θ(t ∣ θ) = ∂S(t ∣ θ)/∂θ, and $\stackrel{d}{\to }$ represents convergence in distribution as n → ∞ for fixed t.

Note that the variance V is controlled by the design e() only through I(e(), θ), hence, from Result 1, only through $I_{\text{sample}}^{\text{dble}}{\mid }_{\text{phase}}^{\text{first}}$ (e(·), θ), given in (7). We call a design that has already been implemented and in particular, in which a double-sample has been obtained via, for example a random double-sample design where e^pilot(·) = constant, a “pilot design.” In a pilot design, the first expectation term in (7) can be estimated by replacing e(Profile_i) with D_i and δ(Profile_i, θ) with δ_i(θ), where

$${\delta }_i\left(\theta \right)\equiv -\left[{\Delta }_i\frac{{\partial }^2}{\partial {\theta }^2}\text{log}P(T_i\mid R_i=0,{\text{Profile}}_i,\theta )+(1-{\Delta }_i)\frac{{\partial }^2}{\partial {\theta }^2}{\text{log Surv}}_{T,R=0}(C_i;{\text{Profile}}_i,\theta )\right],$$ (8)

and taking the empirical average over all observed dropouts; and $P(R_i^{\mathit{obs}}=0\mid \theta )$ can be estimated by the observed proportion of dropouts in the total sample. We refer to a design that has not yet been implemented, but is under consideration as e^candidate(·), a “candidate design.” We can estimate (7) for a candidate design using data from the pilot design by:

$$\frac{1}{n}\sum _{i\mid R_i^{obs}=0}\frac{e^{\text{candidate}}\left({\text{Profile}}_i\right)}{e^{pilot}\left({\text{Profile}}_i\right)}{D}_i{\delta }_i\left(\theta \right)$$

whose expectation equals the expression in (7), and where δ_i(θ) is as defined in (8). In summary, to estimate (7) using data from a pilot design,

$${\widehat{I}}_{\text{sample}}^{\text{dble}}{\mid }_{\text{phase}}^{\text{first}}=\{\begin{array}{cc}\frac{1}{n}\sum _{i\mid R_i^{\mathit{obs}}=0}{D}_i{\delta }_i\left(\theta \right)\hfill & \begin{array}{c}\text{to estimate for a pilot}\hfill \\ \text{(already implemented) design}\hfill \end{array}\hfill \\ \frac{1}{n}\sum _{i\mid R_i^{\mathit{obs}}=0}\frac{e^{\text{candidate}}\left({\text{Profile}}_i\right)}{e^{\text{pilot}}\left({\text{Profile}}_i\right)}{D}_i{\delta }_i\left(\theta \right)\hfill & \begin{array}{c}\text{to estimate for a candidate}\hfill \\ \text{(not yet implemented) design}\hfill \end{array}\hfill \end{array}\phantom{\}}$$ (9)

Based on the above, then, V can be estimated by:

$$\widehat{V}\left(e\right(\cdot ),\widehat{\theta })=f^{\prime }{\left\{{\widehat{I}}_{\text{phase}}^{\text{first}}\left(\theta \right)+{\widehat{I}}_{\text{sample}}^{\text{dble}}{\mid }_{\text{phase}}^{\text{first}}\left(e\right(\cdot ),\theta )\right\}}^{-1}f+g$$ (10)

where ${\widehat{I}}_{\text{sample}}^{\text{dble}}{\mid }_{\text{phase}}^{\text{first}}$ is as in (9), and f, g, ${\widehat{I}}_{\text{phase}}^{\text{first}}$, ${\widehat{I}}_{\text{sample}}^{\text{dble}}{\mid }_{\text{phase}}^{\text{first}}$ are defined as:

$$\begin{array}{cc}\hfill f& =\frac{1}{n}\sum _{i=1}^n{S}_{\theta }(t\mid Z_i,\widehat{\theta })\hfill \\ \hfill g& =\frac{1}{n}\sum _{i=1}^n{\left\{S\right(t\mid Z_i,\widehat{\theta })-\widehat{S}(t\left)\right\}}^2\hfill \\ \hfill {\widehat{I}}_{\text{phase}}^{\text{first}}& =-\frac{1}{n}\sum _{i=1}^n\frac{{\partial }^2}{\partial {\theta }^2}{\ell }_{\text{phase}}^{\text{first}}({\text{Data}}_i;\widehat{\theta }).\hfill \end{array}$$

5 Identifying more efficient designs in practice

5.1 General Procedure

In practice the researcher can use the above methods in the following way to identify a more efficient design strategy.

1. Estimate the distribution of patient characteristics from pilot data using a simple design. Implement the pilot design on a modest scale with a convenient, perhaps a random, double-sampling design, i.e., e(·) =constant. From these pilot data, estimate a model for the patient characteristics T, L, R. Obtain the MLE of the parameters, $\widehat{\theta }$, of such a model.

2. Decide on a class of designs to search. Decide on a set of candidate designs {e} for the larger scale implementation. This set is usually dictated by administrative reasons and so it often fixes a maximal allowable recruitment window (P(C ∣ Z)).

3. Identify a more efficient design. Estimate the best design e(Profile_i) from the set of candidate designs {e}. The best design is the rule e(·) which minimizes the variance V(e(·), θ). The best design can be estimated, using the pilot data, as the design that minimizes the estimated variance $\widehat{V}\left(e\right(\cdot ),\widehat{\theta })$ in (10).

A larger-scale follow-up can then be conducted according to the more efficient design. After the data have been collected, any method of survival estimation that is appropriate for use with double-sampled data can be adopted (e.g., as described in [3] or in Section 3).

5.2 Illustration: Designing PEPFAR program evaluations

In this section, we illustrate identifying a more efficient design using a pilot design from the AMPATH cohort. We use these pilot data to identify a design that uses the patient profiles to more accurately estimate the survival function in larger scale studies with similar characteristics.

1. Estimate the distribution of patient characteristics from AMPATH pilot data using a simple design. We used the AMPATH cohort [3] as pilot data, and considered, based on input from our collaborators for which variables they believe to be predictive of dropout, the following baseline covariates Z: gender, baseline CD4 count, baseline WHO stage, indicator of urban versus rural clinic, and ART start status. We specified logit(R∣Z) as $({\beta }_0^R+{\beta }_1^{R}Z)$; P(T∣R = 1, Z) as log-normal$({\beta }_0^{T1}+{\beta }_1^{T1}Z,{\sigma }_{T0}^2)$; P(L∣R = 0, Z) as log-normal$({\beta }_0^{L0}+{\beta }_1^{L0}Z,{\sigma }_{L0}^2)$; and P(T∣R = 0, L, Z) as a log-normal$({\beta }_0^{T0}+{\beta }_1^{T0}+{\beta }_2^{T0}Z,{\sigma }_{T0}^2)$, left-truncated at L (i.e., T > L). Based on these variables and models, we formulated and used an EM algorithm [13] to estimate the MLE of the parameters. The EM requires specification of the complete data log likelihood (see Appendix). Note that other data distribution models could be explored, so long as software exists to easily fit these models. We in turn estimated the 1-year survival probability at 0.86 (se=0.008).

2. Search within the class of designs based on dropout time and predictor for dropout. We consider the variables Profile_i for selecting whom to double-sample in the AMPATH cohort [3] to be a predictor, P, for dropout and the actual time for dropout L. The former, P, is the linear predictor from a Cox model for dropping out based on the baseline covariates (listed above), with advanced WHO status and male gender being the primary risk factors of patient dropout [8]. Thus, P serves as a single-number summary of factors predictive of dropout.

   In practice to search for a more efficient design, it may be more convenient and insightful to consider double-sampling from discrete groups. Such discretization leads to a convenient estimator of the variance given in Result 2. Moreover, studying the variation in precision across discretized groups can yield generalizable suggestions on how to increase precision. We consider double-sampling within the discretized groups formed by cross-classifying tertiles of the linear predictor for removal (P ) and the tertiles of dropout time (L) (Table 1(a)). The idea is to allow for oversampling of certain groups, but random sampling within groups.

   A total of 3528 patients were observed dropouts. We distributed those dropouts in the cross-classification of L and P so as to classify approximately 390 patients (11%) in each of the nine cells. A total of 621 dropouts were double-sampled. Let $n_k^{\mathit{pilot}}$ denote the number of dropouts that the pilot design double-samples from cell k, k = 1, 2, … , 9. It is interesting to note that in fact, even the original design deviates from being independent of the observed predictors P, L. This deviation does not matter for the validity of estimation of the parameters using our methods, as the latter account for any dependence of the double-sampling on the observed predictors. Denote by n_k the number of dropouts that a candidate design double-samples from cell k, k = 1, … , 9 (Table 1(a)-(b)).

3. Identify a more efficient design. We wish to find the allocation n₁, …, n₉ that minimizes the variance of the survival estimator (2), subject to having a fixed total number n_(D=1) of patients to double-sample, i.e., ${\sum }_{k=1}^9{n}_k=n_{(d=1)}$

Table 1.

Designs for double-sampling and resulting variance of the 1-year mortality estimate with the PEPFAR data described in the text.

(a) Discretized double-sampling (∑k nk fixed)
		Risk for dropout
		low	med	high
Dropout time	short	n 1	n 2	n 3
	med	n 4	n 5	n 6
	long	n 7	n 8	n 9

To do this, we first estimate the components of the variance expression (10). Then, for a fixed double-sample size n_(D=1) = 621, we minimize the estimated variance (10) over possible designs e(·) characterized by Table 1(a). Using the expression of the information I(e(·), θ) from Result 1, it is easy to show that this is equivalent to finding the number of people, n_k, to double-sample from each profile cell k, in order to minimize over all possible designs {n_k} the variance expression

$$f^{\prime }{\left({\widehat{I}}_{\text{phase}}^{\text{first}}+{\widehat{I}}_{\text{sample}}^{\text{dble}}{\mid }_{\text{phase}}^{\text{first}}\right)}^{-1}f+g$$

such that the eigenvalues of $({\widehat{I}}_{\text{phase}}^{\text{first}}+{\widehat{I}}_{\text{sample}}^{\text{dble}}{\mid }_{\text{phase}}^{\text{first}})$ are positive, and where f, g, ${\widehat{I}}_{\text{phase}}^{\text{first}}$ can be calculated from the pilot study based on the definitions in (10), and ${\widehat{I}}_{\text{sample}}^{\text{dble}}{\mid }_{\text{phase}}^{\text{first}}$ can be calculated via:

$${\widehat{I}}_{\text{sample}}^{\text{dble}}{\mid }_{\text{phase}}^{\text{first}}=\frac{1}{n}\sum _k{n}_k\cdot {\stackrel{‒}{\delta }}_k,$$

such that ∑_k n_k = n_(D=1), and

$${\stackrel{‒}{\delta }}_k=\frac{1}{n_k^{\mathit{pilot}}}\sum _{i\in \text{cell}k}{\delta }_i\left(\theta \right)D_i.$$

We impose the condition on the eigenvalues to ensure that the information matrix is positive definite.

We identified the more efficient design shown in Table 1(c) using a Gauss-Seidel-type algorithm to search the design space. In the more efficient design, we observe an oversampling of individuals with short dropout times (L). This confirms the intuition expressed in the Introduction. Also, among individuals with higher risk for dropout in Phase 1, the more efficient design suggests double-sampling both individuals with short and medium dropout times (L). This can be explained by the smaller observed variability of L in these higher risk categories, and so the need to better inform on the regression relations by ensuring that we include in the design enough variability in L.

Although this more efficient design has not yet been implemented, we estimate, using the pilot data, that the potential gain in efficiency associated with the more efficient design compared to the original design is 37% (=100(1 – 4.5/7.1) from Tables 1(b)-(c)). In other words, the follow-up can save 37% of resources for the same precision. This increased efficiency is particularly important when program monitoring and evaluation resources are scarce as it is the case in most PEPFAR-funded HIV care and treatment programs. It is worth noting again that in the original design, among individuals with similar dropout times, the observed double-sampling was not random; this suggests that the potential efficiency gains for an more efficient design relative to a truly random design may be greater than what we estimate.

5.3 Results based on sensitivity considerations

In order to understand better the above results, we conducted a number of additional analyses. First, within the context of the model of Section 5.2 step 2, we changed the predictor set for estimating the linear predictor P of dropout, by removing the ART start status as this had not been decisively important in predicting time to dropout (hazard ratio=1.21, se=0.21, p=.35). Analyses with this new risk index are reported in column “without ART” in Table 2. Second, to examine the influence of the parametric functional forms of the model of Section 5.2 step 1, we estimated the 1-year mortality and standard error of the estimate using the nonparametric estimator of [3, 14] that adjusts for different probabilities of double-sampling in each of the nine levels of the designs in Table 1. These analyses are reported in the rows “nonparametric (estimate, se) in Table 2 for the original design. Third, we also estimated the predicted more efficient design and the estimated variance it would produce for the 1-year mortality if using the modified risk index in which ART is excluded. This design is reported in Table 1(d) and its resulting standard error is reported in the row of “predicted more efficient design” of Table 2 for the parametric estimator (the nonparametric estimator cannot be applied in the predicted more efficient designs because some of its cells are empty).

Table 2.

1-year mortality estimates when changing the design, estimation method, and covariate specification.

design	estimation method	covariates used for risk index
		with ART	without ART
original	nonparametric
	estimate (%)	11.64	11.59
	se (%)	0.85	0.88
	lognormal MLE
	estimate (%)	13.94	13.98
	se (%)	0.84	0.81
predicted more efficient	lognormal MLE
	se (%)	0.67	0.65

The parametric MLE of the 1-year mortality estimate when not using ART in the risk index was 13.98% (se=0.81%) essentially the same as when using ART in the risk index (estimate 13.94%, se=0.84%). The nonparametric estimates were 11.59% (se=0.88%) and 11.64% (se=0.85%) when not using versus when using ART in the risk index, respectively. These are close to the parametric estimates, especially considering that if, instead of changing to parametric estimates, one had changed instead the design to one without double-sampling (with a standard survival analysis where dropouts are censored at time of dropout), the 1-year mortality estimates are dramatically smaller (1.7%, [3]). Finally, the more efficient design when not using ART versus using using ART in the risk index (Table 1 (d) vs. (c)) carry the same message of the need to focus double-sampling to patients with short and medium dropout times; the variance of the 1-year mortality for these two designs are very close to each other.

6 Discussion

The potential utility of imbalanced double-sampling designs for survival estimation has been indicated earlier ([1, Sec 5, par 3]; and [15, Sec. 2]), but without an explicit search for good such designs. We have shown how to characterize the precision of a profile double-sampling design, and how to use a pilot study to find a better design that saves resources which can be allocated for the treatment of additional patients. Based on a parametric likelihood approach, better designs were ones that primarily oversample patients who have short dropout times or have slightly longer L but higher risk for dropout P and either undersample or completely avoid pursuing patients with long dropout times, regardless of the risk of dropout. This strategy, in addition to being intuitive in the statistical sense, provides a reasonable means to determine which dropouts to locate in a preferential fashion. Some of the factors which increase dropout risk, particularly advanced WHO status, are also directly related to the risk of mortality. This is because the mortality rate among dropouts is extremely high [3]. A recent meta-analysis of a number of HIV care and treatment programs, which perform outreach, found up to 87% of located dropouts were deceased [16]. In addition, men have higher dropout rates and consistently worse outcomes compared to women [6]. Thus, oversampling early dropouts and patients at high risk for dropout and poor clinical outcome makes sense, as such a sampling strategy performs outreach on some of the most vulnerable patients in a program.

The estimates of mortality and the estimate of better designs depend on a number of assumptions. First, Conditions 1 and 2 are about the structure of the problem regardless of parametric assumptions. Condition 1 is plausible because we have elicited from the field investigators information about how double-sampling is actually being conducted; Condition 2 is plausible within small time windows where concerns about trends of the epidemic are not substantial. Second, there are dimension reduction and parametric assumptions. Both in earlier work without using dropout time information [3] and also here, in Section 5.3, using dropout time information, we have found that using a nonparametric versus a parametric approach, did not materially change the mortality estimates; and that small changes to the specification of a risk index for dropout provided similar messages about how to improve the design. This provides evidence that the parametric model closely reproduces the nonparametric results and that the design results are relatively robust to how a risk index for dropout is summarized.

Here we considered a fixed double-sample size, and identified a more efficient allocation under this constraint. Alternatively, we could also consider a target precision, and identify the size of the sample and an allocation which minimizes the overall double-sample size or cost. Finally, we note the importance of having a representative double-sample. There is evidence that a representative double-sampling cohort is realistically possible in the setting we consider ([14], [17]). Of course, the larger the representative sample, the more precise the parameter estimates. So we hope that the utility of this design can lead to large scalability.

In our framework, we introduced the concept of a “true dropout” (R). Because the true dropout is a patient characteristic (i.e., independent of the design’s follow-up), its modeling (i.e., what we learn from it) is expected to be more generalizable to other designs (and communicable to researchers of different studies) than the modeling of the observed dropout, which does depend on the design (and could have different meanings across different studies.) For example, the concept of true dropout and L for such a person is important if we were to also treat “Now” (i.e., the longest follow-up) as a possible design factor to manipulate. This remains for future work, but the current framework holds for both that and this current work.

In addition to mortality as a goal, one might also wish to assess a program with the composite event of “death or dropout”. Using standard empirical process (nonparametric) estimation for competing risks, we estimated that 41.9 % (se=0.6%) of the patients either die or dropout after 1 year of follow-up (P(T_i ≤ 1, R_i = 1) + P(L_i < 1, R_i = 0)); and that only 1.3% (se=0.1%) die by year 1 without being lost from observation. Note that both of these probabilities are estimated without the information from double-sampling. The 41.9% rate of the composite event of death or dropout would be appropriate in a setting where dropout would mean almost certain death. This is not the case here, however, where the 13% mortality (based on the double-sampling information) is substantially less than 41.9% (for example, patients who dropout from this surveillance system can be still visiting other physicians not in the system).

As future work, it would be important to develop double-sampling designs and methods that can handle clinical and program constraints. For example, clinical reasons may require the design to double-sampling all patients within a certain subgroup of patients, for example patients who are deteriorating rapidly. In this case, e(Profile_i) = 1 for patients for whom patient characteristics suggest rapid deterioration. Here our methods could be readily extended to select profile double-sampling within the dropouts for whom e(Profile_i) ≠ 1 subject to the constraint that the double-sample already includes those for whom e(Profile_i) = 1. Additionally, it may be that double-sampling is most likely to be both successful (in finding dropouts) and clinically beneficial when efforts are focused on patients whose time of dropout is relatively close to “Now,” which translates to requiring that C_i – L_i ≤ c for some constant c. In this case, e(Profile_i) = 0 for patients with C_i – L_i > c. Our methods would need to be carefully extended to use a likelihood that will leverage the data close to the boundaries of the exclusion regions, using regression discontinuity [18]. If the exclusion regions are large or at the edge of the characteristics space, the missing information can be bounded by upper and lower bounds, as in other missing data settings, e.g., [19, 20]. Finally we could generalize the proposed methods to address double-sampled individuals who are not found. On the field, this problem can be limited by careful planning. At the analysis stage, we could treat any patients still not found as censored conditionally on time-dependent information, and then use sensitivity analyses to assess impact to the results. PEPFAR alone is directly involved in the care of over 11 million patients affected by HIV and AIDS. With over 20% of these expected to be lost during the first year from enrollment [21], any effort, however well-intentioned, to locate all dropouts is doomed to fail out of lack of resources alone. On the other hand, monitoring and evaluation of programs that involve long-term follow-up which, in the case of PEPFAR, is required by law, cannot be performed solely based on the observed non-dropouts [3, 8, 16]. Thus, only sampling techniques are capable of offering means of performing meaningful evaluation of the effectiveness of these programs. Nevertheless, we expect that our proposed designs will be embraced by both Public Health professionals, who monitor and evaluate these programs, as well as clinicians who are focused in improving outcomes for their patients. This is because these designs offer the possibility of significantly reducing the resources required as fewer individuals must be sought, which appeals to the former group, and preferentially outreach some of the patients who are most likely to have poor clinical outcomes, which interests the latter.

In summary, double-sampling designs are useful in using data to address possible nonignorable dropout. The choice of a particular design set may depend on the available staff and infrastructure of a setting. In general, profile double-sampling designs, relative to random double-sampling designs, can help to maximize the impact of limited amounts of resources, which is significant, particularly in resource-limited settings.

(b) Number of people double-sampled in original design (Variance=7:1 × 10−5)
		Risk for dropout
		low	med	high
Dropout time	short	32	79	88
	med	37	102	78
	long	36	88	81

(c) Number of people to double-sample for more efficient design when using ARV (Variance = 4:5 × 10−5)
		Risk for dropout
		low	med	high
Dropout time	short	121	124	15
	med	0	168	193
	long	0	0	0

(d) Number of people to double-sample for more efficient design when not using ARV (Variance = 4:3 × 10−5)
		Risk for dropout
		low	med	high
Dropout time	short	127	86	26
	med	0	183	199
	long	0	0	0