Intrinsic Regression Models for Manifold-Valued Data

Abstract

In medical imaging analysis and computer vision, there is a growing interest in analyzing various manifold-valued data including 3D rotations, planar shapes, oriented or directed directions, the Grassmann manifold, deformation field, symmetric positive definite (SPD) matrices and medial shape representations (m-rep) of subcortical structures. Particularly, the scientific interests of most population studies focus on establishing the associations between a set of covariates (e.g., diagnostic status, age, and gender) and manifold-valued data for characterizing brain structure and shape differences, thus requiring a regression modeling framework for manifold-valued data. The aim of this paper is to develop an intrinsic regression model for the analysis of manifold-valued data as responses in a Riemannian manifold and their association with a set of covariates, such as age and gender, in Euclidean space. Because manifold-valued data do not form a vector space, directly applying classical multivariate regression may be inadequate in establishing the relationship between manifold-valued data and covariates of interest, such as age and gender, in real applications. Our intrinsic regression model, which is a semiparametric model, uses a link function to map from the Euclidean space of covariates to the Riemannian manifold of manifold data. We develop an estimation procedure to calculate an intrinsic least square estimator and establish its limiting distribution. We develop score statistics to test linear hypotheses on unknown parameters. We apply our methods to the detection of the difference in the morphological changes of the left and right hippocampi between schizophrenia patients and healthy controls using medial shape description.

1 Introduction

Statistical analysis of manifold-valued data has gained a great deal of attention in neuroimaging applications [1], [2], [3], [4], [5], [6], [7], [8], [9]. Examples of manifold-valued data that we encounter in medical imaging analysis include the Grassmann manifold, planar shapes, deformation field, symmetric positive definite (SPD) matrices and the medial shape representations (m-rep) of subcortical structures (Fig. 1). Some review papers on the applications of manifold-valued data in medical imaging can be found in a recent special issue of NeuroImage [10]. However, the existing statistical methods for manifold-valued data are primarily developed to estimate intrinsic and extrinsic means, to estimate the structure of population variability, to carry out principal geodesic analysis, and to compare intrinsic (or extrinsic) means across two or more groups [11], [9], [12], [13], [14], [15], [16], [17].

Fig. 1.

Four different manifold-valued data (from the left to the right): deformation field reflecting brain deformation obtained from the registration of either diffusion tensor images (DTIs) or T1 magnetic resonance images (T1 MRIs); principal direction (PD) field reflecting fiber orientations obtained from DTIs; diffusion tensor field reflecting water diffusion along fiber tracts from DTIs; medial shape representations of hippocampi from multiple subjects obtained from the segmented T1 MRIs

Little literature exists for regression analyses of manifold-valued data. The existing parametric and nonparametric regression models for manifold-valued data were primarily developed for 2 (or 3) dimensional directional data [6], [18]. In parametric regression of directional data, parametric distributions, such as the Von Mises distribution, are commonly assumed for directional data, whereas it can be very challenging to assume useful parametric distributions for other manifold-valued data, such as SPD matrices and the m-rep, which can characterize the feature (e.g., shape) of real imaging data [15]. In the nonparametric analysis of manifold-valued data, although smoothing splines have been developed for directional data and planar landmark data, it is computationally difficult to generalize such smoothing splines to other manifold-valued data [6]. Recently, local constant regressions have been developed for manifold-valued data, but these regression models are defined with respect to either the Frechet mean or the geometric median [2], [4].

According to the best of our knowledge, this is the first paper that develops a semiparametric regression model with manifold-valued data as responses on a Riemannian manifold and a set of covariates, such as time, gender, and diagnostic status, in Euclidean space. Our regression model are solely based on the first-order moment, thus avoiding specifying any parametric distributions. We propose an inference procedure to estimate the regression coefficients in this semi-parametric model. We establish asymptotic properties, including consistency and asymptotic normality, of the estimates of the regression coefficients. We develop score statistics to test linear hypotheses on unknown parameters. Finally, we illustrate the application of our statistical methods to the detection of the difference in morphological changes of the hippocampi between schizophrenia patients and healthy controls in a neuroimaging study of schizophrenia.

2 Method

2.1 Review of Regression Models

We consider a dataset that is composed of a response y_i and a p × 1 covariate vector x_i for i = 1, ⋯, n. Responses may be continuous observations in classical linear models, such as age, weight, income, and they may be discrete or ordinal observations, such as differing severity of diseases and disease status (patients v.s. healthy subjects). Covariates may be quantitative, such as age, or qualitative, such as handiness, gender, and presence of risk factors (yes/no).

Regression models often include two key elements: a link function μ_i(β) = g(x_i, β) and a residual ε_i = y_i − μ_i(β), where β is a q × 1 vector of regression coefficients and g(·,·) is an known mapping from R^p × R^q to R. Regression models assume that

$$E[{\epsilon }_i|{\mathbf{x}}_i]=0\text{for all}i=1,\cdots ,n,$$ (1)

where the expectation denotes the conditional expectation of ε given x. Moreover, nonparametric regressions include a link function μ_i = g(x_i), in which g(·) is an unknown function, and a residual ε_i = y_i − g(x_i), for which equation (1) holds.

To carry out statistical inference on β (or g(·)), we need at least three statistical methods. The first one is an estimation method for calculating parameter estimate of β, denoted by β̂. Various estimation methods include maximum likelihood estimation, robust estimation, estimating equations, among many others. The second is to prove that β̂ is a consistent estimator of β and has certain asymptotic distribution (e.g., normal). The third is to develop test statistics for testing the hypotheses:

$$H_0:{\mathbf{h}}_0(\mathit{\beta })={\mathbf{b}}_0\mathrm{v}\mathrm{s}.H_1:{\mathbf{h}}_0(\mathit{\beta })\ne {\mathbf{b}}_0,$$ (2)

where h₀(·) is an r × 1 vector function and b₀ is an r × 1 specified vector. In most applications, we are interested in testing h₀(β) = Hβ = b₀ for a given r × q matrix H [18], [7], [8].

2.2 Intrinsic Regression for Manifold-Valued Data

We formally develop an intrinsic regression model for manifold-valued responses and covariates of interest from n observations. Suppose we observe a dataset {(S_i, x_i) : i = 1, ⋯, n}, where S_i are points on a Riemannian manifold 𝓢 and x_i are covariates of interest in Euclidean space.

The intrinsic regression model first involves modeling a ‘conditional mean’ of an manifold-valued response S_i given x_i, denoted by μ_i(β) = g(x_i, β), where g(·,·), called link function, is a map from R^p × R^q to the manifold 𝓢. Note that we just borrow the term ‘conditional mean’ from Euclidean space. Given two points S_i and μ_i(β) on the manifold ℳ, the intrinsic regression model also define the residual or ‘difference’ between S_i and μ_i(β) to ensure that μ_i(β) is the proper ‘conditional mean’ of S_i given x_i. At μ_i(β), we have a tangent space of the manifold 𝓢, denoted by T_μi(β)^𝓢, which is a Euclidean space representing a first order approximation of the manifold 𝓢 near μ_i(β). Then, we calculate the projection of S_i onto T_μi(β)^𝓢, denoted by Log_μi(β)(S_i), which can be regarded as the difference between S_i and μ_i(β) for i = 1, ⋯, n. If 𝓢 is a Euclidean space, then Log_μi(β)(S_i) = S_i − μ_i(β).

The intrinsic regression model for manifold-valued data is then defined by

$$E[{\text{Log}}_{{\mu }_i(\mathit{\beta })}({\mathbf{S}}_i)|{\mathbf{x}}_i]=\mathbf{0},$$ (3)

for i = 1, ⋯, n, where the expectation is taken with respect to the conditional distribution of S_i given x_i. Model (3) does not assume any parametric distribution for S_i given x_i, and thus it allows for a large class of distributions [15]. In addition, our model (3) does not assume homogeneous variance across all i. This is also desirable for the analysis of imaging measures, such as diffusion tensors, because between-subject and between-voxel variability in the imaging measures can be substantial.

2.3 Estimation

We calculate an intrinsic least squares estimator (ILSE) of the parameter vector β, denoted by β̂, by minimizing the total residual sum of squares given by

$$G_n(\mathit{\beta })=\sum _{i=1}^{n}d{({\mathbf{S}}_i,{\mu }_i(\mathit{\beta }))}^2=\sum _{i=1}^n<<{\text{Log}}_{{\mu }_i(\mathit{\beta })}({\mathbf{S}}_i),{\text{Log}}_{{\mu }_i(\mathit{\beta })}({\mathbf{S}}_i)>>,$$ (4)

where << ·,·>> is an inner product of two tangent vectors in T_μi(β)^𝓢 and d(·,·) is the Riemannian distance function on 𝓢. Thus, let $G_n(\mathit{\beta })={\sum }_{i=1}^{n}d{({\mathbf{S}}_i,{\mu }_i(\mathit{\beta }))}^2,\mathit{\beta ̂}$, β̂ solves the estimating equations given by

$${\partial }_{\mathit{\beta }}{G}_n(\mathit{\beta })=\sum _{i=1}^n{\partial }_{\mathit{\beta }}d{({\mathbf{S}}_i,{\mu }_i(\mathit{\beta }))}^2=\mathbf{0},$$ (5)

where ∂ denotes partial differentiation with respect to a parameter vector, such as β. The ILSE is closely related to the intrinsic mean μ̂_IM of S₁, ⋯, S_n ∈ 𝓢, which is defined as

$${\mathrm{\mu ̂}}_{IM}={\text{argmin}}_{\mu }\sum _{i=1}^{n}d{(\mu ,{\mathbf{S}}_i)}^2.$$ (6)

In this case, μ_i is independent of i and covariates of interest. Moreover, under some conditions, we can establish consistency and asymptotically normality of β̂. A Newton-Raphson algorithm is developed to obtain β̂. Let ∂_βG_n(β) and ${\partial }_{\mathit{\beta }}^2{G}_n(\mathit{\beta })$, respectively, be the first- and second-order partial derivatives of G_n(β). We iterates ${\mathit{\beta }}^{(t+1)}={\mathit{\beta }}^{(t)}+\rho {\{-{\partial }_{\mathit{\beta }}^2{G}_n({\mathit{\beta }}^{(t)})\}}^{-1}{\partial }_{\mathit{\beta }}{G}_n({\mathit{\beta }}^{(t)})$, where 0 < ρ = 1/2^k₀ ≤ 1 for some k₀ ≥ 0 is chosen such that G_n(β^(t+1)) ≤ G_n(β^(t)). We stop the Newton-Raphson algorithm when the absolute difference between consecutive β^(t)’s is smaller than a predefined small number, say 10⁻⁴. Finally, we set β̂ = β^(t). In addition, because $-{\partial }_{\mathit{\beta }}^2{G}_n({\mathit{\beta }}^{(t)})$ may not be positive definite, we use $E[-{\partial }_{\mathit{\beta }}^2{G}_n({\mathit{\beta }}^{(t)})]$ instead of $-{\partial }_{\mathit{\beta }}^2{G}_n({\mathit{\beta }}^{(t)})$ in order to stabilize the Newton-Raphson algorithm.

2.4 Hypotheses and Test Statistics

In medical analysis, most scientific questions of interest involve a comparison of manifold-valued data across diagnostic groups or detecting change in manifold-valued data across time [8], [19]. These scientific questions usually can be formulated as follows:

$$H_0:\mathbf{H}\mathit{\beta }={\mathit{b}}_0\mathrm{v}\mathrm{s}.H_1:\mathbf{H}\mathit{\beta }\ne {\mathit{b}}_0.$$ (7)

We test the null hypothesis H₀ : Hβ = b₀ using a score test statistic W_n defined by

$$W_n={{\mathbf{L}}_n}^T{\mathbf{Î}}^{-1}{\mathbf{L}}_n,$$ (8)

where ${\mathbf{L}}_n=n^{-1/2}{\sum }_{i=1}^n{\mathbf{Û}}_i(\mathit{\beta ̃})$ and $\mathit{Î}=n^{-1}{\sum }_{i=1}^n{\mathbf{Û}}_i(\mathit{\beta ̃}){\mathbf{Û}}_i{(\mathit{\beta ̃})}^T$, in which β̃ denotes the estimate of β under H₀ and Û_i(β̃) is associated with ∂_βG_n(β). It can be shown that W_n is asymptotically χ² distributed.

2.5 Positive Definitive Matrices

We develop an intrinsic regression for SPDs. We introduce the tangent vector and tangent space at any μ ∈ Sym⁺ (m), the space of SPDs [8]. The tangent space of Sym⁺ (m) at μ, denoted by T_μSym⁺ (m), is identified with a copy of Sym(m), the space of symmetric matrices. Then we consider the scaled Frobenius inner product of any two tangent vectors Y_μ and Z_μ in T_μSym⁺(m), which is defined by << Y_μ, Z_μ >>= tr(Y_μμ⁻¹Z_μμ⁻¹). Given the inner product, we can formally construct the Riemannian geometry of Sym⁺(m) [8].

We consider the link function μ(x, β) using the Cholesky decomposition of μ(x, β). For the i−th observation, through a lower triangular matrix C_i(β) = C(x_i, β) = (C_jk(x_i, β)), the Cholesky decomposition of μ(x_i, β) equals μ(x_i, β) = μ_i(β) = C_i(β)C_i(β)^T. We must specify the explicit forms of C_jk(x_i, β) for all j ≥ k in order to determine all entries in μ_i(β). As an illustration, for m = 2, we may choose the 2 × 2 matrix C_i(β) with $C_{11}({\mathbf{x}}_i,\mathit{\beta })=\text{exp}({\mathbf{z}}_i^T{\mathit{\beta }}_{(1)})$, C₁₂(x_i, β) = 0, $C_{21}({\mathbf{x}}_i,\mathit{\beta })={\mathbf{z}}_i^T{\mathit{\beta }}_{(2)}$, and $C_{22}({\mathbf{x}}_i,\mathit{\beta })=\text{exp}({\mathbf{z}}_i^T{\mathit{\beta }}_{(3)})$, where ${\mathbf{z}}_i={(1,{\mathbf{x}}_i^T)}^T$ and β_(k) for k = 1, 2,3 are subvectors of β. We introduce a definition of ‘residuals’ to ensure that μ_i(β) is the proper ‘conditionalmean’ of S_i given x_i. Then, we calculate the residual Log_μi(β)(S_i) given by C_i(β) log(C_i(β)⁻¹S_iC_i(β)^−T)C_i(β)^T. The intrinsic regression is defined in (3).

The first- and second-order derivatives of G_n(β) are given as follows. The a-th element of ∂_βG_n(β) is given by $-2{\sum }_{i=1}^n\text{tr}\{{ℇ}_i(\mathit{\beta }){\mathbf{C}}_i{(\mathit{\beta })}^{-1}{\partial }_{{\beta }_a}{\mu }_i(\mathit{\beta }){\mathbf{C}}_i{(\mathit{\beta })}^{-T}\}$, where ℇ_i(β) = log(C_i(β)⁻¹S_iC_i(β)^−T) and ∂_βa = ∂/∂β_a. The (a, b)-th element of ${\partial }_{\mathit{\beta }}^2{G}_n(\mathit{\beta })$ is given by $-2{\sum }_{i=1}^n\text{tr}\{{\partial }_{{\beta }_b}{ℇ}_i(\mathit{\beta })[{\mathbf{C}}_i{(\mathit{\beta })}^{-1}{\partial }_{{\beta }_a}{\mathbf{C}}_i(\mathit{\beta })+{\partial }_{{\beta }_a}{\mathbf{C}}_i{(\mathit{\beta })}^T{\mathbf{C}}_i{(\mathit{\beta })}^{-T}]\}-2{\sum }_{i=1}^n\text{tr}\{{ℇ}_i(\mathit{\beta }){\partial }_{{\beta }_b}[{\mathbf{C}}_i{(\mathit{\beta })}^{-1}{\partial }_{{\beta }_a}{\mathbf{C}}_i(\mathit{\beta })+{\partial }_{{\beta }_a}{\mathbf{C}}_i{(\mathit{\beta })}^T{\mathbf{C}}_i{(\mathit{\beta })}^{-T}]\}$ where ${\partial }_{{\beta }_a{\beta }_b}^2={\partial }^2/\partial {\beta }_a\partial {\beta }_b$ and ${\partial }_{{\beta }_b}{ℇ}_i(\mathit{\beta })={\int }_0^1\mathbf{h}(s,\mathit{\beta })ds$, in which

$$\mathbf{h}(s,\mathit{\beta })={\{[{\mathbf{S̃}}_i(\mathit{\beta })-{\mathbf{I}}_3]s+{\mathbf{I}}_3\}}^{-1}{\partial }_{{\beta }_b}{\mathbf{S̃}}_i(\mathit{\beta }){\{[{\mathbf{S̃}}_i(\mathit{\beta })-{\mathit{I}}_3]s+{\mathbf{I}}_3\}}^{-1}$$ (9)

and S̃_i(β) = C_i(β)⁻¹S_iC_i(β)^−T.

2.6 Median Representation

We develop an intrinsic regression for m-reps. An m-rep model consisting of k medial atoms can be considered as the direct product of k copies of M(1) = R³ × R⁺ × S(2) × S(2), that is $M(k)={\prod }_{i=1}^{k}M(1)$, where S(2) is the sphere in R³ with radius one [5]. We introduce a tangent space T_PM(1) at the point P = (O, r, n₀, n₁), where O ∈ R³, r ∈ R⁺, and n₀ and n₁ ∈ S(2). The tangent vector U ∈ T_PM(1) takes the form U = (U₀, U_r, U_n0, U_n1), where U₀ ∈ R³, U_r ∈ R, U_ni ∈ R³ and $U_{{\mathbf{n}}_i}^T{\mathbf{n}}_i=0$ for i = 0, 1. The inner product of any two tangent vectors U⁽⁰⁾ and U⁽¹⁾ in T_PM(1) is defined by << U⁽⁰⁾, U⁽¹⁾ >>= U^(0)TU⁽¹⁾. The geodesic distance between P and P₁ = (O₁, r₁, n_0,1, n_1,1) in M(1) is uniquely given by

$$\sqrt{{(O-O_1)}^T(O-O_1)+{(\text{log}(r)-\text{log}(r_1))}^2+{[\text{arccos}({\mathbf{n}}_0^T{\mathbf{n}}_{0,1})]}^2+{[\text{arccos}({\mathbf{n}}_1^T{\mathbf{n}}_{1,1})]}^2.}$$

To introduce an intrinsic regression for m-rep, we need to define a link function μ(x, β) = (μ_O(x, β), μ_r(x, β), μ₀(x, β), μ₁(x, β))^T ∈ M(1), which is a 10 × 1 vector. For instance, we may set μ_O(x, β) = (x^Tβ₁, x^T β₂, x^Tβ₃)^T and μ_r(x, β) = exp(x^Tβ₄). A link function for ${\mu }_k(x,\mathit{\beta })=({\mu }_{0k}^x(\mathit{\beta }),{\mu }_{0k}^y(\mathit{\beta }),{\mu }_{0k}^z(\mathit{\beta }))(k=0,1)$ is based on the stereographic projection given by

$$\frac{{\mu }_{0k}^x}{1-{\mu }_{0k}^z}=g_5({\mathbf{x}}^T{\mathit{\beta }}_{5,k})\text{and}\frac{{\mu }_{0k}^y}{1-{\mu }_{0k}^z}=g_6({\mathbf{x}}^T{\mathit{\beta }}_{6,k}),$$ (10)

where g₅(·) and g₆(·) are known link functions and β_5,k and β_6,k are subvectors of β. The residual Log_{μ(x, β)}(P) is given by

$$(O-{\mu }_O(\mathbf{x},\mathit{\beta }),\text{log}(r/{\mu }_r(\mathbf{x},\mathit{\beta })),{\text{Log}}_{{\mu }_0(\mathbf{x},\mathit{\beta })}(U_{{\mathbf{n}}_0}),{\text{Log}}_{{\mu }_1(\mathbf{x},\mathit{\beta })}(U_{n_1})),$$

where Log_{μ0(x, β)}(U_n0) = arccos(μ₀(x, β)^TU_n0)v/||v||₂, in which v = U_n0 − (μ₀(x, β)^TU_n0)μ₀(x, β).

3 Results

To demonstrate our regression method, we applied our methods to the m-rep shape of the hippocampus structure in the left and right brain hemisphere in schizophrenia patients and healthy controls, collected at 14 academic medical centers in North America and western Europe [19]. There were 56 healthy controls and 238 schizophrenia patients who met the following criteria: age 16 to 40 years; onset of psychiatric symptoms before age 35; diagnosis of schizophrenia, schizophreniform, or schizoaffective disorder according to DSM-IV criteria; and various treatment and substance dependence conditions.

We investigated the difference of m-rep shape between schizophrenia patients and healthy controls while controlling for other factors, such as gender and age. The hippocampi m-rep shape at the 24 medial atoms of the left and right brain were used as the response in our intrinsic regression model. Covariates of interest include Whole Brain Volume (WBV), race (Caucasian, African American and others), age (in years), gender, and diagnostic status (patient or control).

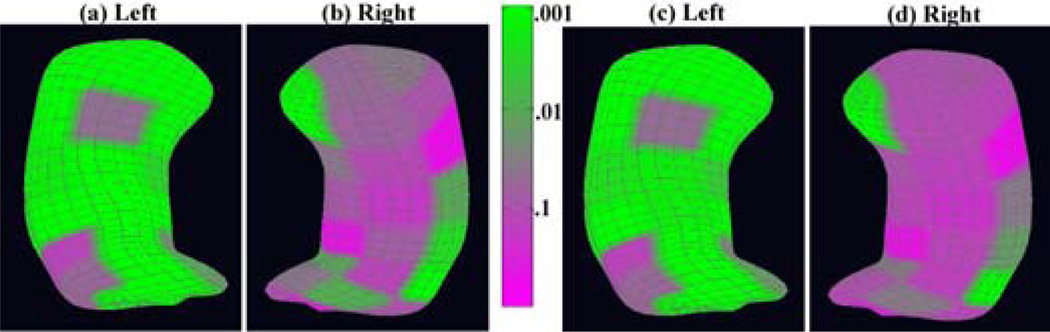
We tested the diagnostic status effect on the whole m-rep structure. We presented the color-coded p-values of the diagnostic status effects across the atoms of both the left and right reference hippocampi in Fig 2 (a) and (b) and the corresponding adjusted p-values using false discovery rate were shown in Fig 2 (c) and (d). We observed large significance area in the left hippocampus, and some in the right hippocampus even after correcting for multiple comparisons.

Fig. 2.

Results for the m-rep shape analysis result mapped to the surface of the hippocampal schizophrenia study: the color-coded uncorrected p–value maps of the diagnostic status effects for (a) the left hippocampus and (b) the right hippocampus; the corrected p–value maps for (c) the left hippocampus and (d) the right hippocampus after correcting for multiple comparisons

4 Discussion

We have developed an intrinsic regression model for the analysis of manifold-valued data as responses in a Riemannian manifold and their association with a set of covariates. We have developed an estimation procedure to calculate the intrinsic least square estimates. We have developed score statistics for testing linear hypotheses on unknown parameters. We plan to apply our method to other manifold-valued data including the Grassmann manifold, planar shapes, and deformation field.