Bidirectional Elastic Image Registration Using B-Spline Affine Transformation

Abstract

A registration scheme termed as B-spline affine transformation (BSAT) is presented in this study to elastically align two images. We define an affine transformation instead of the traditional translation at each control point. Mathematically, BSAT is a generalized form of the affine transformation and the traditional B-Spline transformation (BST). In order to improve the performance of the iterative closest point (ICP) method in registering two homologous shapes but with large deformation, a bi-directional instead of the traditional unidirectional objective / cost function is proposed. In implementation, the objective function is formulated as a sparse linear equation problem, and a sub-division strategy is used to achieve a reasonable efficiency in registration. The performance of the developed scheme was assessed using both two-dimensional (2D) synthesized dataset and three-dimensional (3D) volumetric computed tomography (CT) data. Our experiments showed that the proposed B-spline affine model could obtain reasonable registration accuracy.

I. INTRODUCTION

As a spatial normalization procedure for two images, which could be acquired at different times or from different modalities, the objective of an image registration operation is to find an optimal transformation to align two given images in the same coordinate system. The motivation is typically to compare the morphological variations of two images. There have been numerous algorithms [1–3] developed for this purpose in the past, particularly in the area of medical image analysis [4–7]. A relatively comprehensive review of the available methods can be found in [8–10]. In methodology, a registration scheme usually consists of three primary components:

1. A transformation model: A transformation model represents the spatial relationship between a given fixed (reference) image and a given moving (source or warped) image. There are two types of transformation models, namely rigid / affine transformation and elastic transformation. A rigid model is typically characterized by three translation (i.e., x, y, z) and three rotation (i.e., θ₁, θ₂, θ₃) parameters; and an affine model has additional three scaling and three shearing parameters. Generally, a rigid / affine model aligns pre-identified landmark features globally [11–13]. Although the rigid / affine registration is relatively robust against local minima, it usually has a limited accuracy because the local geometric difference is ignored. In contrast, the elastic approach aims to warp local geometric features of a target image for alignment with a reference image. It could be based on either a dense non-parametric model or a parameterized function model. Many of available elastic registration methods [14–17] were a refinement of either the Demons algorithm [14] or the B-spline method [18]. For example, Rueckert et al. [19] proposed a hierarchical transformation model in which a global affine transformation was first established and a B-spline based freeform deformation was performed. Chui et al [20] combined the affine transformation and the thin plate spline (TPS) transformation. Others include Arsigny et al.’s log-euclidean polyaffine model (LEPT) [21–22] and an extension of LEPT proposed by Taquet et al [23]. Compared with the rigid/affine approach, the elastic method represents a more complex deformation but may be trapped in local minima [9].

2. An objective / cost function: In image registration, an objective function is defined as the criterion for quantitatively assessing the similarity of two aligned images. The criterion could be based on either intensity or features. The intensity-based function aims to elastically align two images according to their underlying intensity patterns. The widely used intensity-based criteria include sum of squared difference (SSD) [24], cross correlation (CC) [25], ratio image uniformity [26], and mutual information (MI) [27]. Specific constraints (e.g., volume or topology preservation [28]) may be imposed on the intensity-based registration for better alignment. For example, Christensen and Johnson [29–30] used inverse consistency as a regularization constraint, while other investigators utilized the Jacobian of the transformation [31] or deformable mapping [32] to preserve the topology. Unlike the intensity-based method [33–35], the feature-based registration method [36–39] aligns two images by identifying the corresponding structural landmark features, which could be points, lines, contours, or their combination. The feature-based objective function is widely defined as the Euclidean distance from the warped features to the fixed features. The unidirectional characteristic doesn’t assure an inverse consistency. Obviously, knowledge of the corresponding features between the target image and the source image is critical for the feature-based registration.

3. An optimization operation: In order to optimize the objective function in a global or local manner, an optimization procedure is needed. For a feature-based objective function, the iterative closest point (ICP) method [40] is widely used. An intensity-based objective function could be optimized using choices such as a gradient descent method [41] or quasi-Newton minimization method with bounds (L-BFGS-B) [42] algorithm. In most applications, whereas the objective functions are not convex, additional efforts [43–44] are needed to reduce the liability of an optimization trapped in local minima. The ICP method only considers one directional cost function and could not ensure one-to-one correspondence between the fixed point set and the moving point set. Although it was developed initially for rigid registration, its direct application to non-rigid registration problems might lead to aberrant results. A couple of approaches [20][45][46][47] were developed by other investigators to address this issue. For example, Chui et al [20] developed a point matching algorithm (RPM). The basic idea was to relax the correspondence variable to be in the interval of [0,1], rather than being binary valued. Myronenko et al. [47] described a probabilistic model that treated the point registration as a maximum likelihood (ML) estimation problem. Other approaches included the Gaussian mixture models (GMM) [45][46], where the registration problem was defined as aligning two Gaussian mixtures by minimizing the L2 distance between two Gaussian mixtures. Recently, in order to reliably handle outliers in both point sets, Sang et al. [48] used a bidirectional expectation–maximization (EM) process to estimate the deformation parameters.

In this study, we proposed a bidirectional B-spline affine transformation (BSAT) model. Unlike the traditional B-spline methods, each control point is defined as an affine transformation. A bidirectional distance cost is used to formulate the objective function, where both errors from moving image to fixed image and from fixed image to moving image are considered. Finally, the objective function is reformulated as a sparse linear system. Detailed descriptions of the developed algorithm and its quantitative performance evaluations as well as its comparison with other approaches follow.

II. METHOD AND MATERIAL

A. B-Spline Affine Transformation (BSAT)

A transformation from the target (moving) image to the fixed image is defined as a mapping f : → . Given a point p_j =[x_j, y_j, z_j]^T in a moving image where 0 ≤ x_j, y_j, z_j ≤1, its mapping f(p_j) in the fixed image is computed using

$$f(p_j)=A(p_j){\widehat{p}}_j$$ (1)

where p̂_j = [x_j, y_j, z_j,1]^T, T denotes transpose of a matrix. A(p_j) is an affine transformation matrix function with a matrix size of 3×4, which is the weighted sum of a set of affine transformation matrices:

$$A(p_j)=\sum _{i=1}^{M}g(p_j,B_i)B_i.$$ (2)

${\{B_i\}}_{i=1}^M$ are the control points and each control point B_i is an 3×4 affine transformation matrix. g(p_j, B_i) ≥ 0 is the weight of the pair of point p_j and control point B_i. For each point p_j, ${\displaystyle \sum _{i=1}^M}g(p_j,B_i)=1$. Here, the weighting function g(p_j, B_i) is defined by the quadratic B-spline basis; and the proposed model is called B-Spline Affine transformation (BSAT). The proposed BSAT model is a more generalized model of the B-Spline transformation (BST), in which each control point is treated as a displacement / deformation. If the left three columns of the transformation matrix B_i of each control point are replaced with an identity matrix

$$B_i=\left[\begin{array}{cccc}1& 0& 0& {\text{dx}}_{\mathrm{i}}\\ 0& 1& 0& {\text{dy}}_{\mathrm{i}}\\ 0& 0& 1& {\text{dz}}_{\mathrm{i}}\end{array}\right],$$ (3)

then the BSAT model degenerates to a BST model. The BSAT model is also a more generalized model of the affine transformation. If all the transformation matrices ${\{B_i\}}_{i=1}^M$ has the same elements, the model will degenerate to an affine registration. For each control point, the BSAT model has twelve parameters, while the BST has three parameters. This means that the BSAT model may provide more complex transformation (freedom) than the BST with the same set of control points.

B. A Bi-Directional Objective/Cost Function

An objective function consists of an external cost function and an internal cost function

$$E(f)=(1-\alpha )E_{\mathit{error}}(f)+\alpha E_{\mathit{rigidness}}(f)$$ (4)

where E_error measures the registration errors, and E_rigidness measures the rigidness of the registration. The parameter 1 > α ≥ 0 is a tradeoff between the registration accuracy and the rigidness of the registration. In practical applications, feature identification procedures may be used to identify some corresponding features (e.g., points, surfaces, or curves) depicted on given images. Generally, the features could be represented using a set of points; hence, the problem can be formulated as:

Input: two sets of feature points identified separately from a fixed image S_f and a moving image S_m. For each moving point p_j, a weight w_j ≥ 0 may be associated to quantify the priority or the importance of this point.

Output: a spatial transformation f defined in (1) by which E is minimized.

The registration error can be summarized as

$$E_{\mathit{error}}=\sum _{j=1}^L{w}_j{(f(p_j)-q_j)}^2$$ (5)

w_j ≥0 is the weight of the moving surface point p_j, q_j is the corresponding point to p_j in fixed feature point set. The traditional methods typically determine the corresponding point q_j in fixed point set S_f by minimizing the distance between q_j and f(p_j), i.e.,

$$q_j=arg\underset{q\in S_f}{min}{\Vert f(p_j)-q\Vert }^2.$$ (6)

They only consider a unidirectional cost from the moving feature points to the fixed feature points and ignore the cost from the fixed feature points the moving feature points. Also, there may be multiple moving feature points corresponding to the same closest point in the fixed feature point set. In cases such as the one in Figure 1(a), the transformed moving points (warped points) will shrink to a line. Despite the minimal cost in this case, the underlying correspondence between the two point sets is not correct.

Figure 1.

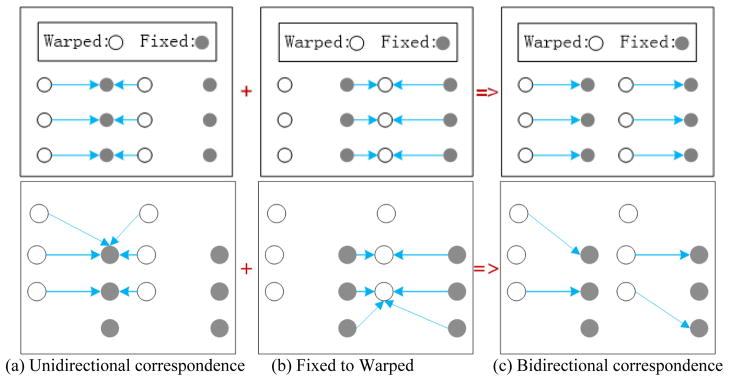
Illustration of the difference between the bidirectional correspondence and the unidirectional correspondence using two examples.

In order to overcome this issue, we consider the cost from the fixed points to the moving points as well. This bidirectional strategy is similar to the Hausdorff distance [49], which measures the closest distance between two point sets. Here, we introduced a concept termed as active pair. (p_j, q_j) is an active pair between the moving point set S_m and the fixed point set S_f, if (p_j, q_j) meets the following three conditions:

1. p_j, q_j have the same label

2. $q_j=arg\underset{q\in S_f}{min}{\Vert f(p_j)-q\Vert }^2$ or $p_j=arg\underset{p\in S_m}{min}{\Vert f(p)-q_j\Vert }^2$;

3. For any other pairs (p_j, q) and (p, q_j) that satisfy condition (a) and (b), the inequality holds: || f(p_j) −q_j ||² ≥|| f(p) −q_j ||² and || f(p_j) −q_j ||² ≥|| f(p_j) −q ||².

where the “same label” is determined before the registration procedure. The feature points selected from the fixed and moving images are classified into different categories. The points from the same category have the same label. For example, we can classify feature points into different categories in terms of pulmonary lobe boundary and the boundary points on the same lobe will have the same label.

To find the active pairs {(p_j, q_j) }, the following steps are performed:

1. For each fixed point, find its nearest moving point with the same label and assign their connection / edge to both points;

2. For each moving point, find its nearest fixed point with the same label, assign their connection / edge to both points;

3. For each connection/edge f(p_j)q_j, (p_j, q_j) is an active pair if length of f(p_j)q_j is greater than all the other edges assigned to p_j and q_j.

The new scheme considers registration errors from both directions and ensures a symmetrical “one-to-one” correspondence. The correspondence remains the same when we switch the fixed and moving point sets. Each point in the fixed point set and each point in the moving point set only belong to one active pair. p_j is an active moving point, if (p_j, q_j) is an active pair. We note that, generally, not all the moving points are active and not all the fix points are active. In an extreme case, there may be only one active pair initially. However, in practice, more than half of the moving points are active. Two examples in Figure 1 are used to illustrate the potential advantage of the proposed bi-directional correspondence as compared to the traditional unidirectional correspondence. It can be seen from the examples that bi-directional correspondence provides a more reasonable correspondence between the warped object and the fixed object.

The rigidness cost function E_rigidness measures the variation of the transformation matrix A, and it is defined as

$$E_{\mathit{rigidness}}={\iiint }_{x,y,z}{\Vert \frac{\partial A}{\partial x}\Vert }_F^2+{\Vert \frac{\partial A}{\partial y}\Vert }_F^2+{\Vert \frac{\partial A}{\partial z}\Vert }_F^2\mathit{dxdydz}$$ (7)

where ||•||_F denotes the Frobenius norm. The rigidness E_rigidness=0, if A is an identical matrix function. If α → 1, all the transformation matrices ${\{B_i\}}_{i=1}^M$ will be the same and the registration will degenerate to an affine registration.

C. Optimization Procedure

The iterative closest point (ICP) method is widely used to find the correspondences between two point sets. ICP “pushes” the moving feature points to their corresponding fixed feature points iteratively. Given our bi-directional model, as the examples in Figure 1 show, a corresponding fixed feature point is not necessarily the closest point of the moving feature point. For each iteration, the energy function E is a quadratic polynomial of ${\{B_i\}}_{i=1}^M$, thus we can use a gradient descent method to compute ${\{B_i\}}_{i=1}^M$ by minimizing E. In this study, we directly obtain the optimal ${\{B_i\}}_{i=1}^M$ by solving a least square problem with a sparse coefficient matrix. Detailed implementation is described below.

Let a matrix X =[B₁, B₂,…, B_M]^T with a size of 4M ×3 include the transformation matrices ${\{B_i\}}_{i=1}^M$ of all the control points. The matrix $Q={[\sqrt{w_1}{q}_1,\sqrt{w_2}{q}_2,\dots ,\sqrt{w_L}{q}_L]}^T$ has a size of L ×3. Here, M is the number of B-spline control points, and L is the number of active moving points. We define a sparse matrix U with a size of L×4M, each entry of U is given by

$$U[j,4(i-1)+k]=\{\begin{array}{l}\sqrt{w_j}g(p_j,P_i)x_j,k=1\hfill \\ \sqrt{w_j}g(p_j,P_i)y_j,k=2\hfill \\ \sqrt{w_j}g(p_j,P_i)z_j,k=3\hfill \\ \sqrt{w_j}g(p_j,P_i)1,k=4\hfill \end{array},$$ (8)

where i =1,2,…, M; j =1,2,…, L. Substitute U, X, and Q into the registration error function (5), we have $E_{\mathit{error}}={\Vert UX-Q\Vert }_F^2$. Similarly, the rigidness cost function in Equation (7) is a quadratic equation of X thus can be rewritten in a compact form E_rigidness= X^TVX, where V is a semi-definite matrix with a size of 4M ×4M. The optimization problem (4) is then rewritten as the following least square problem

$${min}_X(1-\alpha ){\Vert UX-Q\Vert }_F^2+\alpha X^{T}VX,$$ (9)

The above problem is equivalent to the following linear equation

$$[(1-\alpha )U^{T}U+\alpha V]X=(1-\alpha )U^{T}Q.$$ (10)

Whereas U^TU +V is a sparse matrix, thus we can use some efficient sparse solver, such as SuperLU [50], to efficiently solve the sparse linear equation.

D. Some Implementation Details

In order to find the bidirectional correspondent feature points efficiently, we divide the whole point sets (e.g., image pixels or voxels) into a set of sub-volumes, and the searching for the nearest feature points is performed within the nearest sub-volume. In practice, the identified feature points may not distribute uniformly in space. If the conventional B-spline is used as the transformation model, there may be too many feature points around some control points, while no feature points around some other control points. Hence, we used an Octree-spline scheme instead of the conventional B-spline. First, an axis-aligned bounding box (AABB) is used to establish a volumetric grid system for an image. If a sub-volume contains too many feature points, it is then divided into eight smaller boxes with the same size. This subdivision operation is repeated until there is no sub-volume that contains too many feature points. For each sub-volume, its center is selected as a corresponding control point for the spline transformation. In the optimization, the iteration would stop at step T if the energy function E_T is larger than 0.999 E_{T −1}.

E. Performance Evaluation

As we mentioned, the innovations of our approach lies in two aspects, namely (a) a B-spline transformation model where an affine transformation is defined at each control point, and (b) a bidirectional objective / cost function. To verify the potential advantages, we designed and compared the following four methods on four synthesized 2D datasets (Section II. E. 1):

• Method-AB: In the transformation model, an affine transformation (A) is defined at each control point; and the proposed bidirectional distance (B) is used to compute the cost.

• Method-AS: In the transformation model, an affine transformation (A) is defined at each control point; and the traditional unidirectional distances (S) is used to compute the cost.

• Method-DB: In the transformation model, a translation transformation (D) is defined at each control point; and the proposed bidirectional distance (B) is used to compute the cost.

• Method-DS: In the transformation model, a translation transformation (D) is defined at each control point; and the traditional unidirectional distances (S) is used to compute the cost.

We implemented all the above four methods for both two-dimensional (2D) synthesized images and three-dimensional (3D) volumetric images (i.e., chest computed tomography (CT) examinations).

E.1 Synthesized 2D datasets

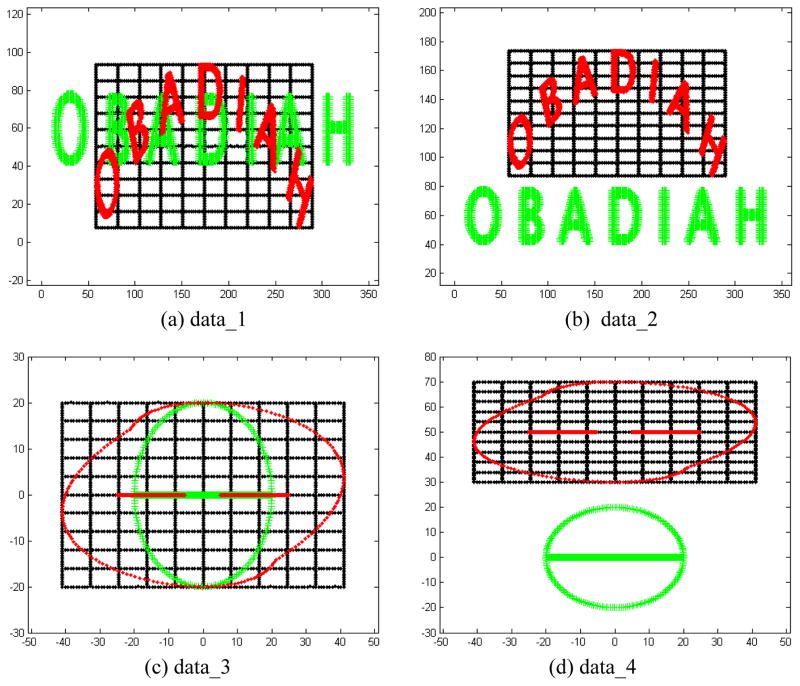
Four synthesized 2D datasets, as shown in Figure 2, were generated to assess the above derived four methods. The points in green indicate the fixed point set, the points in red indicate the moving point set, and the points in black indicate the grid points of the moving point set. “data_1” and “data_2” are sampled from the capital letters “OBADIAH”. Each of them has 2786 fixed feature points and 2786 moving feature points. In “data_3” and “data_4”, there are some missing points in the moving image. In “data_1” and “data_3”, the fixed and moving images have the same center, while in “data_2” and “data_4”, the centers of the fixed and moving images are significantly different.

Figure 2.

Four synthesized 2D datasets for performance assessment.

Whereas the regularized coefficient α is an important parameter in the deformation models, we tested each model with 99 different α values ranging from 0.01 to 0.99 with an interval of 0.01. For each α, the root mean squared error (RMSE) of the registration was computed. The registration errors of both directions were computed:

$${\mathit{Error}}_{\alpha }=\sqrt{\frac{1}{N_m}\sum _{i=1}^{Nm}{(T_{\alpha }(p_i)-q_i)}^2}+\sqrt{\frac{1}{N_f}\sum _{j=1}^{N_f}{(T_{\alpha }(p_j)-q_j)}^2}$$ (11)

where N_m and N_f are the number of the moving feature points and the fixed feature points, respectively, T_α denotes an optimized transformation for a given α, p_i is a moving feature point, and q_i is a fixed feature point that has the minimal distance to T(p_i). The mean, the maximum and the minimum of the 99 Error_α as well as their standard deviations were computed.

E.2. Volumetric lung CT examinations with follow up scans

Forty low-dose CT examinations of twenty patients were specifically selected from a database as a result of the University of Pittsburgh Lung Cancer Specialized Program of Research Excellence (SPORE). These examinations were all pathologically verified lung cancer cases with the tumor location information. They were acquired from 2002 to 2009 using LightSpeed Plus 4-MDCT or LightSpeed Ultra 8-MDCT scanners GE Healthcare. The low-dose CT acquisition protocol varied slightly depending on patient size. Exposure settings ranged from 120 to 140 kVp, 29.7±10.7 mAs, with section reconstruction interval ranged from 0.625 mm to 5 mm, and in-plane pixel size from 0.50 mm to 0.98 mm. Images were reconstructed with 512×512 pixel matrices using the GE Healthcare “lung” reconstruction kernel. Each patient had two scans with a time interval from 4 months to 68 months (mean=22 months). In each scan, a lung nodule was identified by a radiologist [51]. The utilization of these CT examinations is to assess the performance of the developed scheme in pulmonary nodule (tumor) registration. Pulmonary lobes, which were identified by a computerized scheme described in [52], were used as the feature points for registration purpose. The registration error was assessed by computing the mean, maximum, and minimum Euclidean distance (ED) between the mass centers of the corresponding nodules between two follow-up scans. The mass centers were estimated using an automated nodule segmentation scheme [53].

E.3. Registration of inspiration and expiration CT examinations

Twenty-pairs of CT examinations with full inspiration and at suspended full expiration were randomly selected from a Lung Tissue Research Consortium (LTRC) study at the University of Pittsburgh. These examinations were acquired without contrast and with subjects holding their breath for approximately 15 seconds at both end-inspiration and end-expiration. The protocol was the same for the inspiration and expiration acquisition for each participant. Images were reconstructed to encompass the entire lung field in a 512×512 pixel matrix. More details on the protocol can be found in [54]. The lobe boundaries were also employed as feature points. To assess the accuracy of the developed methods in expiration and inspiration registration, we used a computerized scheme described in [55] to identify the airway trees and their bifurcation points in the first four generations. The correspondences of the points were firstly established automatically by computing their Euclidean distances after registration performed and then verified / corrected by an expert. The Euclidean distances between the corresponding bifurcation points after registration operation are computed as indices of the registration error.

F. Parameter setting in the experiments

In our experiments, all the feature points were assigned with the same weight 1. For the CT examinations, an adaptive and dynamic α was selected in this study as α = 0.9/(T +1), where T was the step number of the registration. The initialized grid volume system had a grid size of 4×4×4. For the octree spline scheme, if a subvolume contains more than 2000 feature points, it was divided into eight smaller subvolumes. The number of the feature points was around 1 million, and number of the control points was around 2000. Since each control point in the B-Spline affine transformation has more freedom than the B-Spline displacement, more control points were used in the B-Spline displacement so the two transformations had the same degree of freedom.

III. RESULTS

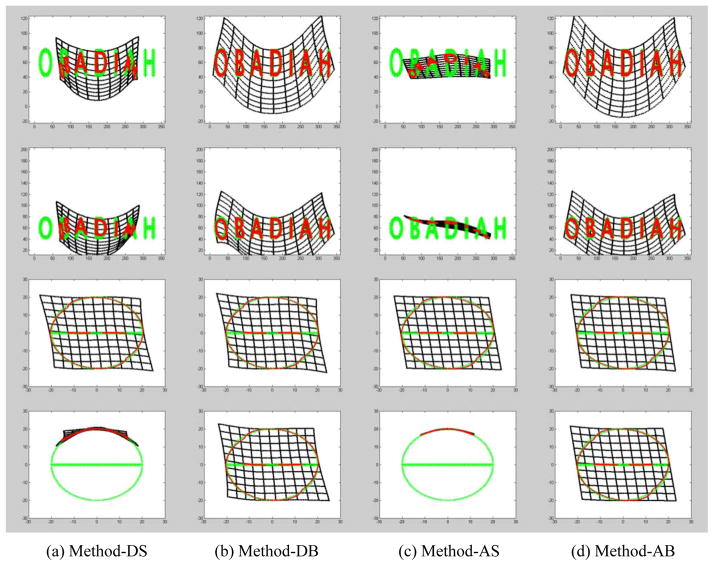
First, the registration errors of the four derived methods on the four synthesized 2D datasets are summarized in Table I. At the same time, the final registration results are shown in Figure 4. It can be seen that Method-AB has the smallest error consistently. In particular, as the registration errors of Method-DB and Method-AB show, the introduction of the bi-directional objective function increase the registration accuracy significantly. The results in Figure 4 demonstrated that the methods with unidirectional cost functions (i.e., Method-DS and Method-AS) were trapped in local minima when there is complex structures (e.g., d-data_1) or there are large displacements between two images (e.g., data_4). Second, for the forty lung CT examinations with follow-up scans, the registration errors of the 40 depicted nodules (tumors) were summarized in Table II. It can be seen again that Method-AB has the smallest registration error with a mean of 6.9±3.3 mm. Third, when studying the registrations between the paired inspiration and expiration CT examinations, as shown in Table III, we found that Method-AB had the best performance with a mean error of 2.7±1.0 mm. An example is shown in Figure 5.

Table I.

Registration errors of the four methods on the four synthesized image datasets. (unit: pixel)

Data	Methods	Mean	Std	Max	Min (α)
data_1	Method-DS	26.9	1.50	27.7	24.2 (0.12)
	Method-DB	4.11	2.23	7.33	0.62 (0.32)
	Method-AS	27.1	0.41	27.6	25.1 (0.04)
	Method-AB	2.01	2.12	7.00	0.56 (0.37)
data_2	Method-DS	29.6	0.83	31.4	25.3 (0.07)
	Method-DB	14.4	4.98	25.1	1.86 (0.83)
	Method-AS	30.1	0.77	31.1	27.7 (0.06)
	Method-AB	10.2	4.23	20.4	0.90 (0.78)
data_3	Method-DS	1.36	0.29	2.75	1.05 (0.18)
	Method-DB	1.15	0.28	2.57	0.76 (0.21)
	Method-AS	1.22	0.15	1.40	0.99 (0.08)
	Method-AB	0.93	0.10	1.15	0.52 (0.20)
data_4	Method-DS	19.4	0.28	19.8	18.4 (0.68)
	Method-DB	1.23	0.32	2.44	0.89 (0.22)
	Method-AS	19.1	0.06	19.2	19.0 (0.72)
	Method-AB	1.17	0.30	1.89	0.60 (0.20)

Figure 4.

The registration results on the four synthesized datasets in each row.

Table II.

Registration errors of lung nodules. (unit: mm)

	Mean	Std	Max	Min
Affine	8.3	5.2	17.5	1.5
Method-DS	7.9	4.8	16.1	1.3
Method-DB	7.1	4.6	17.5	1.1
Method-AS	8.0	4.1	14.6	1.5
Method-AB	6.9	3.3	14.7	0.3

Table III.

Registration error of airway tree bifurcations. (unit: mm)

	Mean	Std	Max	Min
Affine	3.45	1.24	6.36	1.53
Method-DS	3.09	1.10	5.54	1.35
Method-DB	2.94	1.03	4.40	1.07
Method-AS	3.08	1.07	5.31	1.24
Method-AB	2.72	0.95	4.07	1.03

Figure 5.

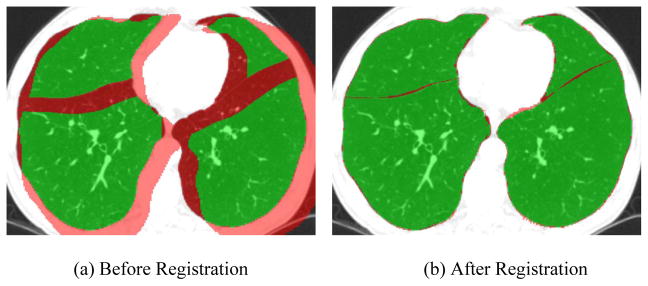
An example of the registration result after the application of Method-AB to a pair of inspiration and expiration CT examinations acquired on the same subjects. The overlays in green represented the area where the lobes identified in different examinations were overlapped and the overlay in red represented the area where there was no overlapping between these lobes.

In computational efficiency, the proposed registration scheme converged approximately in 30 iterations in the volumetric CT registration in our experiments. For each iteration, it took the scheme about 10 seconds to identify all the corresponding feature points. Additional 15 seconds were needed to solve the sparse linear equation problem, when there were around 2000 control points. Therefore, it totally took 10 ~ 15 minutes to perform the registration.

IV. DISCUSSION

In this study, we developed a new registration scheme termed as B-spline affine transformation (BSAT). The innovation of this scheme lies in two aspects: (1) defining an affine transformation instead of the traditional translation at each control point, and (2) defining a bi-directional instead of the traditional unidirectional objective / cost function. Mathematically, the developed B-spline affine transformation (BSAT) is a generalized model of the traditional B-Spline transformation (BST). The primary difference between the B-spline model with affine transformations and the B-spline model with displacements or translation are their regularizations. The regularization of the former model as in Equation (7) gives the transformation more freedom so that the transformation will have a zero cost on the regularization when displacing, rotating, rescaling, and shearing. On the contrary, the regularization of the models with displacements gives the transformation much fewer freedoms, where the transformation has a zero cost on the regularization only with translation. Although the B-spline model also has zero cost in the model constraint when using the bending energy (second order constraint), the second order constraint might be more sensitive than the first order constraint used in the B-spline affine model. As our experiments demonstrate, the affine transformation defined at the B-spline control points is capable of obtaining smaller registration errors than the traditional displacement. The traditional ICP methods use a unidirectional cost function that always pushes the moving feature points to the fixed feature points. In contrast, the proposed bidirectional cost function not only pushes the moving feature points to the fixed feature points but also pull the moving feature points away from the fixed feature points at the same time, depending on which direction will lead to a smaller cost. In our experiments, bidirectional cost energy decreases faster than the unidirectional cost energy and converges to smaller values (an example is shown in Figure 6).

Figure 6.

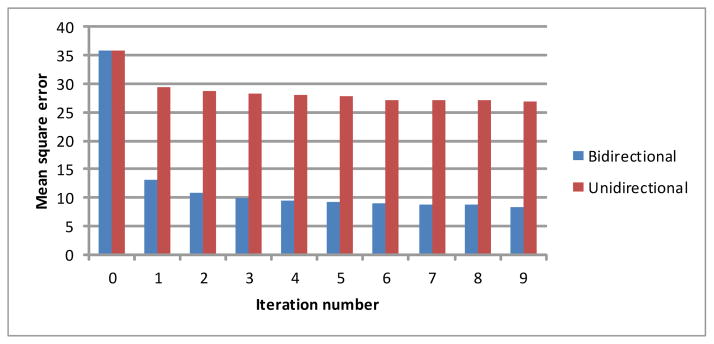
A comparison between the unidirectional and bidirectional correspondence on data_1.

The proposed B-spline affine transformation shares some similar properties as the polyaffine transformation [21–23]. Both of them are defined as a composition of M affine transformation and could be used to solve a sparse linear system. Without considering the objective function and the optimizations, a B-spline affine transformation can be regarded as a special model of the polyaffine model when using the B-spline control points as anchor points and using B-spline basis as the weight function. However, they are different in some aspects. First, the BSAT model was proposed for feature based registration while the polyaffine transformation was proposed for intensity based registration. Second, the polyaffine model requires a preprocessing to find anchor points while the BSAT identifies the control points directly. Third, they have different objective functions. In addition, the two linear systems have different dimensions when optimizing the objective function. For example, the BAST and the polyaffine models solve the linear systems with coefficient matrices of size 4M*4M and 12M*12M, respectively, where M is the number of the control/anchor points.

In concept, the proposed bidirectional energy function can be regarded as a variant of the Hausdorff distance. As compared with the available work such as Sang et al.’s [48], the underlying motivation of our approach and its strategy in implementation are different. For example, Sang et al. proposed the bidirectional update processing to improve the finite mixture model (FMM) in the presence of outliers (noises) in both fixing and moving point sets. We proposed the bidirectional energy in order to achieve an efficient elastic registration for homologous structures when there is large deformation. In addition, the bidirectional update processing proposed by other investigators was implemented in a way where the roles of the moving points and the fixed points were NOT fixed for two given point sets, namely X and Y. In other words, in one iteration, the point set X is treated as the fixed point set and Y as the moving point set; while in the next iteration, the point set X is treated as the moving set and Y as the fixed set. The parameters and the positions of these points were updated in each iteration. This procedure was repeated until the parameters converge. In contrast, in our proposed model, the roles of the moving points and the fix points were fixed, and the bidirectional energy was represented and solved in a single objective function.

In most applications, diffeomorphic registrations are desirable because a diffeomorphism is a globally one-to-one smooth and continuous mapping with derivatives that are invertible (i.e. positive Jacobian determinant) [56–57]; otherwise, the underlying topology may be changed after registration. Detailed descriptions of the BST models and their solution can be found in [56–57]. In the proposed BSAT model, although diffeomorphism is not guaranteed, an implied soft constraint is imposed in the regularization term in Eq. (7).

In implementation, whereas the moving feature points are often not on the integer grids when searching bi-directionally for the corresponding feature points, it may not be proper to use the distance transform to improve the computational efficiency. Hence, we proposed to divide the volume into a set of sub-volumes. Our experiments showed that this sub-division strategy achieved a reasonable efficiency in registration. In addition, the selection of the regularization parameter α is critical in the registration model. If α is too small, the deformation will easily be trapped in local minima, especially when the mass centers of the two images for alignment are far away to each other (e.g., “data_2” and “data_4” in Figure 2). If α is too large, the regularization will dominate the objective function and the deformation will lead to larger error. In practice, there are several ways to address these problems. For example, when performing the pulmonary nodule registration, we align the lung volume centers for initialization. Another way to avoid the α selection is to set a large α (e.g., 0.99) at the first iteration, and then make α decrease progressively until the registration converges towards a predefined small value (e.g., 0.1). In this way, the registration will not easily stop at local minima and may ultimately lead to a relatively high accuracy.

V. CONCLUSION

In this study, a new registration scheme is proposed to align two images based on feature points. The affine transformation is used to replace the traditional displacement at each B-spline control point, and a bidirectional distance cost function is used to replace the traditional unidirectional distance cost function. Experiments on both 2D and 3D image data showed that the proposed B-spline affine model could obtain reasonable registration accuracy.

Figure 3.

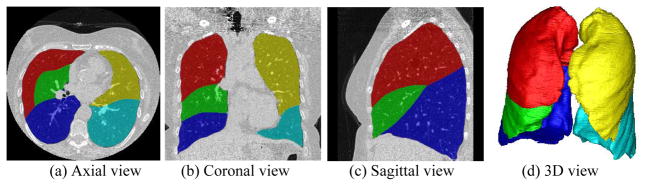
An example demonstrating the performance of the lobe segmentation scheme [50].