Theory for plasticity of face-centered cubic metals

Significance

The ultimate goal of materials science can be reached only from a thorough understanding of the underlying physics of the materials properties. Accordingly, the present global need for high-technology metallic materials strongly depends on the development of robust theoretical understandings that can help to elucidate and optimize their performance. Although plastic deformation is a common denominator in many of these problems, no reliable microscopic theory of plasticity has been presented to date. We demonstrate that fundamental concepts in atomic theory provide a unified solution to plasticity and invite multidisciplinary contributions to deepen and extend the scope to a number of engineering applications. The present work will form a solid basis for many scientific and engineering disciplines.

Abstract

The activation of plastic deformation mechanisms determines the mechanical behavior of crystalline materials. However, the complexity of plastic deformation and the lack of a unified theory of plasticity have seriously limited the exploration of the full capacity of metals. Current efforts to design high-strength structural materials in terms of stacking fault energy have not significantly reduced the laborious trial and error works on basic deformation properties. To remedy this situation, here we put forward a comprehensive and transparent theory for plastic deformation of face-centered cubic metals. This is based on a microscopic analysis that, without ambiguity, reveals the various deformation phenomena and elucidates the physical fundaments of the currently used phenomenological correlations. We identify an easily accessible single parameter derived from the intrinsic energy barriers, which fully specifies the potential diversity of metals. Based entirely on this parameter, a simple deformation mode diagram is shown to delineate a series of convenient design criteria, which clarifies a wide area of material functionality by texture control.

Elastic deformation of metals is fully described by Hooke’s law, connecting stress and strain via the usual elastic parameters. In contrast, plasticity is a property that originates from dislocations and involves transitions over various competing energy barriers. A phenomenological description of the plastic regime based merely on the stacking fault energy (SFE) has been widely used by material scientists (1–11), even though it is not at all clear whether such an equilibrium property can really capture the complexity of plastic deformation. To try to mend this situation, researchers have introduced the so-called generalized planar fault (GPF) energy, which comprises several intrinsic energy barriers (IEBs) and thus provides detailed information on the deformation process itself (12, 13). Nevertheless, the GPF energy has not yet been fully recognized because of its inherent difficulty in experimental validation (14). In the present paper we solve this and introduce an approach that is fully transparent, where there are no such ambiguities.

Face-centered cubic (fcc) metals possess three distinct deformation mechanisms: stacking fault (SF), twinning (TW), and full slip (SL) (2, 5–7, 15). Many studies tried to relate the deformation of fcc metals to the GPF energy. For example, the competition between TW and SL was explained by a relative change between the intrinsic energy barriers, assuming the activation of the lowest barrier mode (16–18). However, such a simplified picture was found to be inadequate to elucidate the simultaneous activation of different modes seen in experiments (2, 5, 6, 15). It has emerged that additional factors should be taken into account in conjunction with the GPF energy for describing the deformation behavior.

The microstructure of materials, such as grain size and orientation, is known to influence the plastic deformation mechanism (1, 15, 19–23). In nanocrystalline metals, the grain boundary-mediated process becomes dominant (24, 25) but the size limit of the dislocation activation is extended to smaller grains at high-pressure conditions (26). However, for the conventional materials with coarse grain sizes it is found that all dislocation-mediated deformation modes are activated irrespective of the grain size and the grain orientation plays an important role in the deformation modes (21–23, 27, 28). Namely, in materials under a uniaxial shear stress, grains experience different load conditions and thus may activate different deformation modes, depending on their orientation. Here, we used molecular dynamics simulations (29, 30) to address the grain orientation effect on the deformation modes of fcc metals.

Results and Discussion

In Fig. 1, we show the GPF energies and deformation behaviors of Cu, Al, and Mn with various shear directions. For each material, the GPF energy and deformation simulations were obtained with the same interatomic potential for consistency. We defined the SFE (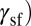, unstable stacking fault energy (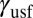), and unstable twinning fault energy (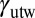) in the GPF energy curve. Because of the sixfold symmetry of the fcc (111) plane, directions from [] (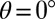) to [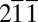] (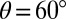) cover all possibilities of the resolved shear stress on the (111) plane. We find that for Cu and Al, having a positive 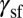, a preexisting SF evolves into TW at low angles and SL is activated at high angles. Twinning and full slip are favored with a comparable weight for Cu, whereas SL is dominant for Al. Both of these scenarios are in line with experiments (31, 32). Note that in both Cu and Al the SL energy barrier 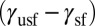is lower than the TW barrier 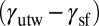and thus a direct comparison of the IEBs cannot account for the activation of twinning.

Fig. 1.

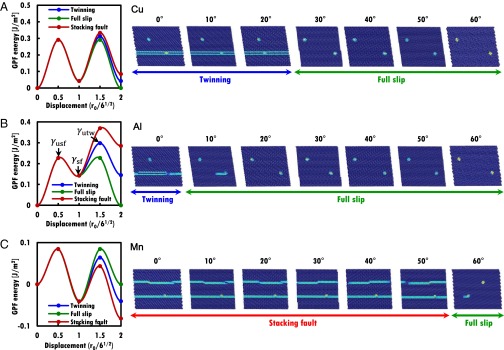
Generalized planar fault energy and activation of deformation mode by varying the shear direction. The stacking fault energy (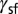), unstable stacking fault energy (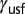), and unstable twinning fault energy (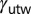) are defined in the energy profile. (A) For Cu, twinning and full slip are activated in a comparable weight because their energy barriers are similar in size. (B) Full slip is dominantly activated in Al, except a small portion of twinning around shear direction of 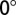. (C) Mn is metastable in the fcc structure and thus stacking faults are generated most exclusively, but full slip can also be observed near the shear direction of .

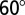The deformation behavior of Mn in Fig. 1C is different from those of Cu or Al. Twinning disappears and stacking fault becomes a dominant deformation mode. The easy activation of SF can be understood by considering that the stacking fault barrier 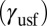in Mn is the lowest among the IEBs. Because Mn has a negative 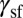, successive generation of SF would eventually transform the metastable fcc phase into a hexagonal close-packed lattice (5–7). Most surprisingly, at high angle the SL mode is also activated in Mn. For Cu and Al, one may argue that twinning is the minor mode having the second lowest energy barrier. However, such an interpretation fails for Mn because its SL barrier is the highest.

Activation of a higher energy barrier mode, while missing a lower one, demonstrates that the effect of shear direction can override the IEBs. Taking into account the shear directionality, we note that the increase of the effective shear stress along a particular direction stimulates the activation of the corresponding deformation mode (27, 28) and thus the energy barrier can be considered to be normalized. Accordingly, we transform the IEBs into the effective energy barriers (EEBs) as

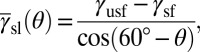where 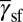, , 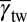and 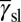denote the EEBs of stacking fault, twinning, and full slip, respectively, and 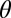is measured from the stacking fault easy direction 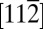. The angle of 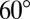in the SL mode corresponds to the change of direction at the SFE point in the GPF energy path to activate a trailing partial dislocation, whereas the direction is retained for the additional stacking fault and the twinning. Although these formulations are similar to those of the critical resolved shear stress, the EEB is conceptually more intuitive and provides a previously unidentified way of predictive analysis, demonstrated below.

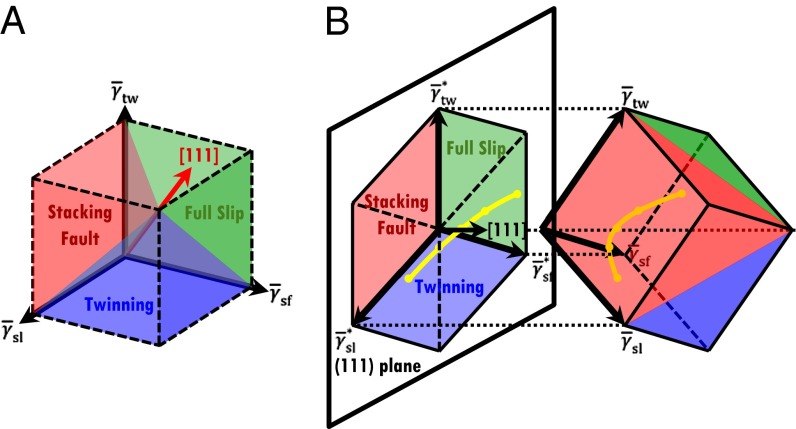
Using the EEBs, one can construct a deformation mode map (DMM) by assuming the activation of the lowest EEB mode. The three effective energy barriers are taken to make a rectangular coordinate as shown in Fig. 2A. The criteria of activating deformation modes identify three planes of the deformation mode boundaries. Hence, the map is partitioned into three distinct regions of stacking fault, twinning, and full-slip mode in which the corresponding energy barrier is the lowest. In the blue region, for example, the twinning mode is favored because 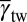is lower than 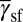and 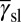. Similarly, the stacking fault mode is favorable in the red region and full slip in the green region. Because all boundary planes for which two EEBs are equal contain the 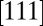direction, it is convenient to examine the DMM in a 2D projection perpendicular to the 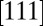direction as shown in Fig. 2B.

Fig. 2.

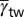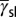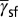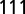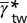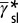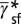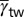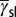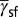Deformation mode map. (A) The deformation mode map is constructed by a rectangular coordinate with three effective energy barrier axes: , , and of twinning, full slip, and stacking fault, respectively. (B) The deformation mode map is projected into the () plane. , , and are the projection lines of , , and , respectively. The yellow line depicts a variation of the effective energy barriers for a given material. This 2D deformation mode map simplifies the determination of deformation mode activation.

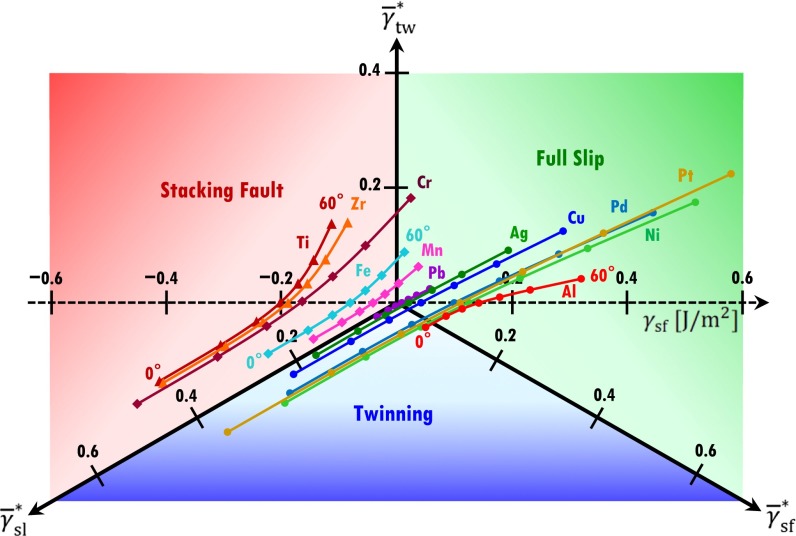
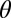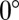In Fig. 3, we display the 2D-DMM for several elementary metals in the fcc structure. Each line of a given metal is the trajectory of the EEBs by varying the shear direction from to 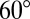. For Mn, the trajectory is located on the SF region for 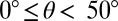and SL is restricted to 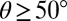. Full slip is dominant in Al, except for twinning at 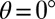. Copper is observed as an intermediate material with TW and SL having similar preference. The above DMM analysis is in agreement with the results in Fig. 1, indicating that the proposed EEBs can be reliably used to explore deformation mechanisms of fcc metals.

Fig. 3.

Effective energy barriers in the 2D-deformation mode map. Each energy barrier trajectory in units of joules per square meter 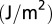passes a single straight line at the shear direction of 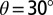, which coincides with the SFE, 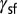. Materials with a large negative 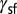(e.g., Ti and Zr) deform exclusively into the stacking fault mode irrespective of the applied shear direction. Materials with small negative 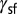(e.g., Mn) can activate full slip together with stacking fault. For positive 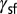, the stacking fault mode disappears and twinning emerges with increased full-slip activation (e.g., Cu). Upon further increase of 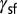, mostly full slip is activated (e.g., Al).

We observe that all EEB trajectories from the DMM pass a single plane at the shear direction 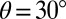. This fact is depicted by a dashed line in the middle of the 2D-DMM (Fig. 3), corresponding to the plane described by 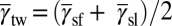(33). It is important to note that this projection line overlaps the SFE line on the DMM. In other words, 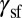of a given material corresponds to the point where the EEB trajectory crosses this line. Materials with 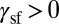(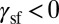) are located at the right (left) side of the SFE line and activate SL or TW (SF or SL), depending on the shear direction.

It is interesting to note that the above scenario derived from the IEBs shows a correlation of the deformation modes with the SFE. This reveals the physical basis behind the classical phenomenological deformation mode diagram based entirely on 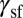(5–7). However, it is also evident in the DMM that 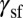is not a comprehensive parameter of deformation. For instance, Ni and Al with similar 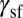behave rather differently in the DMM; Ni activates TW much easier than Al. Therefore, the IEBs cannot be ignored in the deformation process.

The SFE line imposes a constraint among the three IEBs. Thus, one can describe the GPF energy with two energy parameters. Accordingly, we draw a modified DMM in Fig. 4A by setting the intrinsic slip barrier to unit 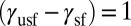. We find that the trajectories of materials are well organized in the modified map, defining an accessible range of energy barriers with forbidden regions. The parameter line at the center of the map represents the shear direction of 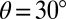and also the ratio of the SFE to the intrinsic slip barrier, 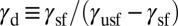. Once this ratio is known, the entire trajectory of that material is determined because no trajectories cross each other.

Fig. 4.

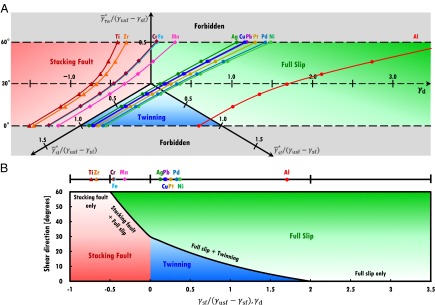
Normalized deformation mode map and deformation mode diagram. (A) The deformation mode map in Fig. 3 is scaled by the full-slip energy barrier, 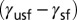. Energy barrier trajectories are rearranged in a constrained form, which defines material-independent straight lines for each shear direction. The dimensionless parameter, 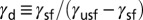, across the center of the map defines the entire energy trajectory of a given material. (B) The parameter 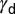enables generating a single-parameter deformation mode diagram. Critical points of 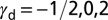identify four different classes of materials deformation: stacking fault only (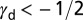), stacking fault with full slip (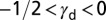), full slip with twinning (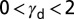), and full slip only ().

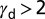Several critical values can be discovered on the parameter line, which classify deformation characteristics of materials. Metals with 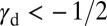(Ti, Zr) activate only SF regardless of the grain orientation. In the range of 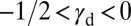(Cr, Fe, Mn) SL appears together with SF, depending on the shear direction. The other materials for which the ground state is the fcc structure have 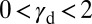. In this region, TW can be observed together with SL. Finally, 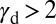corresponds to the pure SL deformation mode region. Aluminum is near the critical point 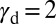and shows SL dominantly with a negligible portion of TW. We conclude that 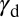is a fundamental parameter of plasticity because it fully specifies the characteristic deformations of materials.

Based on 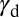, we can now put forward a deformation mode diagram as shown in Fig. 4B. Critical values of 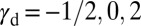divide the parameter space into four regions, categorizing materials according to their deformation properties. An interesting trend about the twinning fraction is observed in the diagram. The fraction of twinning can never be larger than one-half for the uniaxial tensile stress. This finding can be understood by the fact that the TW barrier is always higher than the SL barrier for positive 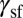because 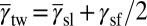from the constraint 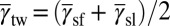. Although low 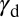is favorable for TW, negative 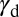or 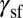suddenly activates SF instead of TW. Furthermore as reflected by the EEB, the preferential direction of TW is the same as that of SF. Therefore, TW and SF are exclusive of each other. We should emphasize that lowering only 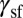does not ensure a considerable tendency of twinning.

The introduced deformation mode diagram is equally valid for elementary metals and complex solid solutions. As an example, we consider the case of the Cu-Al system. Although pure Al does not show TW, Al addition to Cu significantly enhances the twinning activity. Using the previously reported ab initio data (17), we obtain 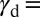0.29, 0.13, and 0.04 for Cu-Al alloys encompassing 0 atomic percent (at.%), 5.0 at.%, and 8.3 at.% Al, respectively. In contrast to many other twin-ability indicators, the above trend of 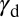clearly quantifies the increased tendency for TW with Al doping without ambiguity.

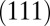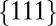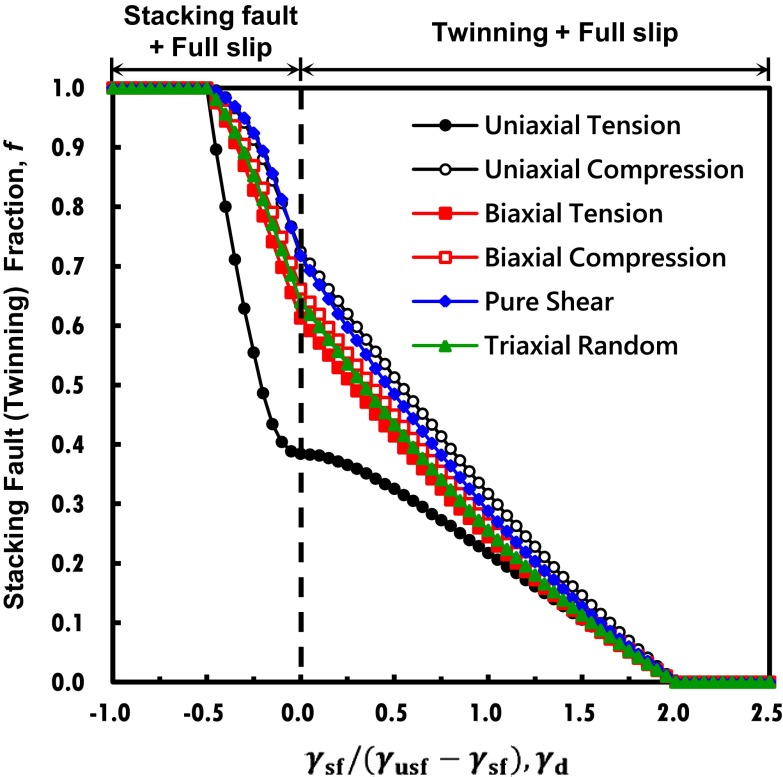
Although the above is a consideration of the deformation modes in singly oriented planes, the discussion can be readily extended to the general situation in which all of the crystallographically equivalent planes are involved in deformation. For this case, a given stress tensor is transformed to obtain the resolved stress on each 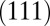plane. The plane with the largest Schmid factor (34) would first activate the SF and subsequent deformation modes. In Fig. 5, we used a Monte Carlo method to generate a number of randomly oriented single grains and using the Schmid factor and EEBs, we evaluated the fraction of the number of grains in each deformation mode of nontextured polycrystalline materials under various applied stresses. It is observed that the stress condition gives rise to a deviation of the deformation mode diagram of Fig. 4B. The uniaxial tension (compression) induces the highest (lowest) fraction of full slip. 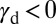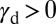In other words, the activation of SF and TW for and , respectively, is minimized under the uniaxial tension, which is in good agreement with experiments (22).

Fig. 5.

Deformation mode fraction of random textured polycrystalline fcc metals under various stress conditions. Uniaxial tension induces the largest activation of full-slip mode.

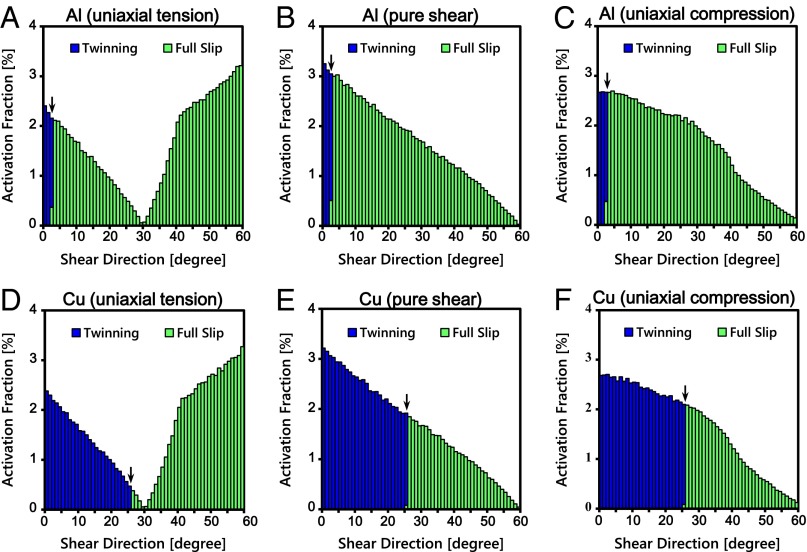
However, these results do not diminish the role of 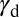as the characteristic parameter of materials deformation. Fig. 6 shows the angular distribution of the activated deformation mode of polycrystalline Al and Cu. The shear direction is measured from the SF easy direction on each 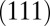plane with the resolved stress. The critical angle of the twinning deformation is 3° and 26° for Al and Cu, respectively, which is an intrinsic material property and does not depend on the shear condition. Meanwhile, it is remarkable that the stress type regulates the shape of the angular distribution of the deformation mode as reflected in Fig. 5. If desired, a well-defined applied stress can control the total fraction of the deformation mode without changing the material composition.

Fig. 6.

Angular distribution of activated deformation mode for Al (A–C) and Cu (D–F) under the applied shear conditions of uniaxial tension (A and D), pure shear (B and E), and uniaxial compression (C and F). The critical shear direction of the twinning (marked by an arrow) is independent on the shear condition.

Because the stress tensor can be identified by three principal stresses (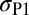, , 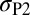and 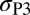), we tried to map the fraction of activated deformation modes on the surface of the principal stress sphere. Fig. 7 shows the maps for polycrystalline Cu, Al, and Mn with randomly oriented grains. The position on the sphere denotes the stress type normalized to the unit 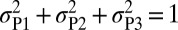and the activated mode fraction is represented with gradient colors. Whereas only a few stress conditions are shown in Fig. 5, the sphere map covers the total stress conditions so that the optimized stress can be checked directly. As an example, Cu reaches almost 70% fraction of twinning in the dark blue region in Fig. 7A. The uniaxial compression condition corresponds to 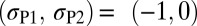and 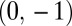in the map. These stress conditions give about 65% of TW for Cu near the twinning optimal region (see also Fig. 5). However, the wide area far from the uniaxial compression is available in the map for the twinning optimization.

Fig. 7.

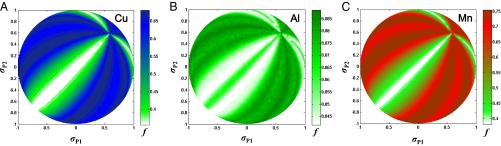
(A–C) Deformation mode fraction in the space of the principal stress for Cu (A), Al (B), and Mn (C). The fraction 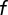of deformation modes is obtained assuming random grain orientation. It denotes the fraction of TW for Cu and Al and SF for Mn. The principal stresses are normalized to 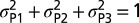and only hemispheres with positive 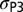are shown due to symmetry. For example, the uniaxial compression condition is 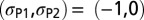and .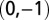

Computational Methods

We performed molecular dynamics simulations by using the modified embedded-atom method of interatomic potentials (29, 30). For deformation simulations, supercell structures of about 54 × 54 × 48 ∼ 140,000 atoms were constructed with a 2D-periodic boundary condition in which extrinsic effects from grain boundaries and surfaces were avoided. To accommodate shear stress, two line defects were inserted in the supercell as partial dislocation sources. Without loss of generality, the simulation started with a prescribed stacking fault on the plane encompassing one line defect; the other line defect was left free. Uniaxial shear stress was applied along the direction of the (111) planes. The shear stress activated one of three deformation modes via generation of a dislocation at one of two line defects. The line defect left free of stacking fault acted as a source of the leading partial dislocation for generating an additional stacking fault and the other one could nucleate twinning partial dislocation for twinning or trailing partial dislocation for full slip. This way, the prepared supercell was in such a condition that the three deformation modes could compete with each other to be activated based on their due likelihood. Deformation simulations were performed at low temperature, below 10 K. We kept strain rate ∼10⁷ s^–1, which is relatively lower than that of a usual molecular dynamics simulation. To minimize the effect of strain rate, the system was statically relaxed at each time step.

Conclusions

The disclosed deformation theory is a perspicuous formulation of plasticity of fcc metals and alloys and establishes a route toward functionality mining of materials through texture control. It is demonstrated that 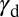is a prime parameter to characterize materials for plastic deformation. The present theory can be applied within the domain of conventional structural materials with large grain sizes (1, 15, 19, 20). Future works are expected to incorporate the effects of grain size, grain boundary structure, temperature, and strain rate. We also believe that deformation mechanisms of other structures such as body-centered cubic and hexagonal close-packed could be treated with the concept of the EEB.

Our theory opens a way to probe the GPF energy by dedicated experiments. The SFE can be found by conventional methods (7, 8) and the value of 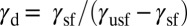can be determined by measuring the number of grains deformed in different modes after applying a stress on a polycrystalline material (22, 23) or by inspecting the orientation range for activating deformation modes in a single crystal (21). Finally, one can make use of the constraint equation 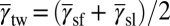to complete the GPF energy. It is expected that the scientific community will extend our understanding by experiments following the above procedure. On the other hand, for engineering purposes, it is recommended to use 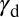, as it contains considerably more information than the conventional SFE.