Figure 3. Graphical models for Discretized Sequentially Markov Coalescent (DSMC) models.

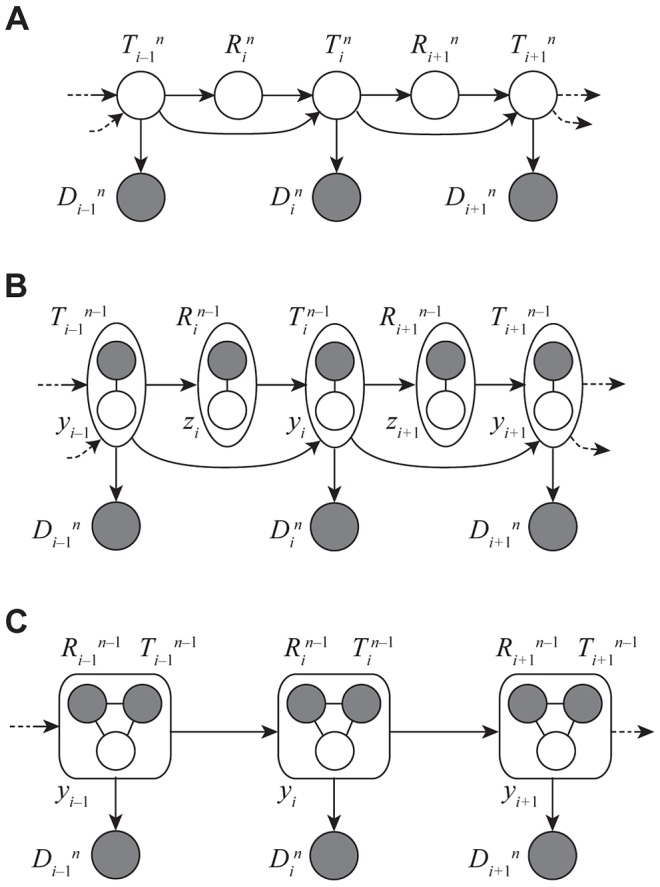
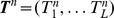(A) Full DSMC model for samples with local trees, , recombinations, 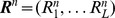, and alignment columns, 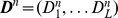. Together, 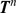and 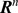define an ancestral recombination graph, 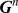. Solid circles indicate observed variables and empty circles indicate latent variables. Arrows indicate direct dependencies between variables and correspond to conditional probability distributions described in the text. Notice that the 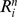variables can be integrated out of this model, leading to the conventional graph topology for a hidden Markov model. (B) The same model as in (A), but now partitioning the latent variables into components that describe the history of the first sequences (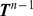 and 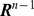) and components specific to the th sequence (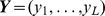 and 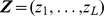). The 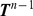and 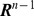variables are represented by solid circles because they are now “clamped” at specific values. A sample of 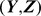represents a threading of the th sequence through the ARG. (C) Reduced model after elimination of 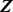by integration, enabling efficient sampling of coalescent threadings 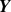. This is the model used by the first step in our two-step sampling approach. In the second step, the 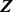variables are sampled conditional on 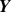, separately for each 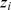. In this model, the grouped nodes have complex joint dependencies, leading to a heterogeneous state space and normalization structure, but the linear conditional independence structure of an HMM is retained.