Impact of MRI head placement on glioma response assessment

Abstract

Diagnosis of progressive disease or (partial) response during tumor treatment is based on manual size estimates of enhancing tumor area: An expert measures two perpendicular diameters of the enhancing tumor region in a single MRI slice with the largest enhancing area. This paper analyzes the reliability of the area measure with respect to head placement in the MRI scanner and compares it with 3D volume measures in a dataset of 8 subjects (5–7 follow-up scans) with high-grade glioma. We show that the manual area measure is highly sensitive to position changes, with a root mean squared error of 22%, compared to volume estimates with less than 5% error. In our simulated study using the 2D manual measurements, the majority of subjects would have been incorrectly diagnosed with progressive disease without any true anatomical changes. These results highlight the urgent need for revised and more reliable response assessment criteria such as increased slice resolution, 3D volume analysis and percent change computation with respect to an average of patient specific longitudinal measurements instead of a single measurement to define progression or response.

1 Introduction

The diagnosis of tumor progression and response in treatment, drug trials or natural disease is primarily based on imaging markers. In neuro-oncology, tumor size changes are typically estimated by quantifying the radiographic response rate in longitudinal MRI follow-up sessions. The same response assessment criteria, introduced primarily for CT scans in 1990 by Macdonald et at. [6], are still at the core of the revised criteria recommended by the Response Assessment in Neuro-Oncology Working Group (RANO) for high-grade [11] and low-grade glioma [2]. Tumor size is defined to be the product of the maximal perpendicular diameters of contrast enhancing tumor on post-gadolinium T1 (in high-grade gliomas) or of the visible lesion on T2 or FLAIR imaging (in low-grade gliomas) in a single MRI slice. Clinical MRI scans with about 5mm thick slices are commonly employed, where an expert selects the slice with the largest tumor component for the manual cross-diameter measurement.

Both low and high-grade glioma can have very irregular shapes and grow anisotropically. Therefore, it can be expected that varying the slice orientation and location, due to positional changes of the head in the scanner, may have a significant impact on the reliability of tumor size estimates derived from linear measurements. Furthermore, 3D volume measurements of manually delineated regions are more reliable, but also affected by partial voluming effects, particularly in images with thick slices (i.e. > 3mm).

In clinical MR imaging, there are methods that attempt to ensure consistent image orientation and slicing across sessions. An MR technologist may conduct a manual alignment to landmarks. Yet, manual methods are time consuming, have limited accuracy and are prone to inter- and intra-operator variability. Automated alignment mechanisms, such as the Siemens AutoAlign procedure [3,1] perform this alignment on the scanner without operator intervention and are usually based on automated landmark or atlas alignment. However, these techniques are prone to failure in difficult pathological cases that distort the normal anatomy, such as a tumor. A lesion is usually not present in the subjects that were used to create the atlas and may also prevent the detection of anatomical landmarks. Furthermore, these methods can exhibit increased variability in the presence of changing anatomy such as tumor proliferation, infiltration or necrosis. For example, we have quantified the registration error by comparing the AutoAlign results with ground truth correspondence established on 1mm isotropic images post acquisition in 38 high-grade glioma patients with 5 to 27 visits each. We found a maximal median alignment error of 62mm across visits within a single subject and a median error across all subjects of 20mm, indicating frequent failure of AutoAlign in tumor images.

Given the limited reliability of manual or automated slice prescription on the scanner, it becomes important to analyze the reliability of derived imaging biomarkers such as the 2D perpendicular diameter product. The extent of the variability caused by different image slice orientation and positioning upon derived imaging biomarkers is largely unknown. A recent study [9] simulating different image acquisition conditions in low-grade glioma found 2D cross-diameter measurements to be very sensitive to position and slice thickness changes. In this study we focus on high-grade glioma, the most common form of malignant primary brain tumors in adults. We simulate treatment assessment in a trial by mapping and reslicing a high-resolutional baseline image in 8 patients to different head positions. Instead of simulating positional differences by varying slice orientation at pre-defined degrees around a fixed axis, as described in [9], we reslice according to the real head position of these patients in their (5–7) follow-up visits. This procedure induces realistic rotation and translation differences and thus simulates a longitudinal study where the depicted anatomy remains fixed across time and only the slice position and orientation changes. Figure 1, for example, shows the same input image resliced to three different head positions. We quantify the influence of the different slicing on both 2D perpendicular diameter measurements and volume estimates to study the reliability of these imaging biomarkers for treatment assessment.

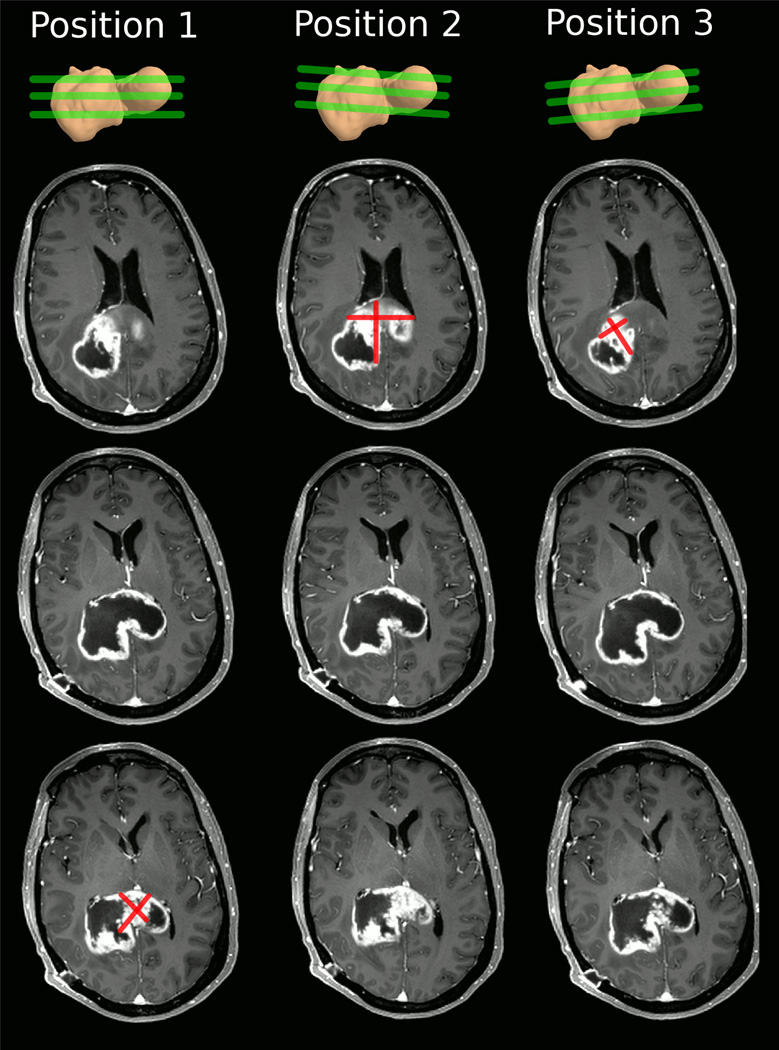
Fig. 1.

Example of measuring perpendicular diameters of the identical tumor in three different head positions (columns). The top row depicts the irregular 3D tumor shape and approximate location of the imaging slices. For each head position we show horizontal slices at the superior, middle, and inferior tumor regions (rows). Depending on the position of the head (and resulting slice position), the identical tumor appears to look different in the images, affecting location and size of the nodule with the largest diameter. Note, that RANO measurements should not include the cystic center.

2 Material

2.1 Patients

Serial MRI scans were obtained at baseline and then weekly for 6 weeks during standard involved-field radiation with temozolomide in 8 patients with newly diagnosed glioblastoma. The study was IRB approved and all patients signed informed consent prior to participating. All patients had to have at least 10mm of contrast enhancing disease to be eligible.

2.2 MRI

1mm isotropic (256 × 256 × 176) multi-echo MPRAGE (MEMPRAGE) images [4] were obtained in all patients at baseline and 5 to 7 follow-up sessions on a Siemens TimTrio scanner (3 Tesla) with a 32-channel head coil after administration of 0.1 mmol/kg contrast agent (gadolinium).

3 Methods

Using the MEMPRAGE images, we constructed highly accurate registrations across time. For each subject i, we computed the rigid transformation T_ij (rotation and translation) that aligns the baseline scan to each follow-up MEMPRAGE scan at time point j via a robust registration procedure [7]. This registration method has been specifically designed to detect and account for potentially large confounding local intensity changes, for instance induced by enhancing tumor or necrosis, resulting in a highly accurate alignment of the images compared to other methods.

3.1 2D RANO Measurements

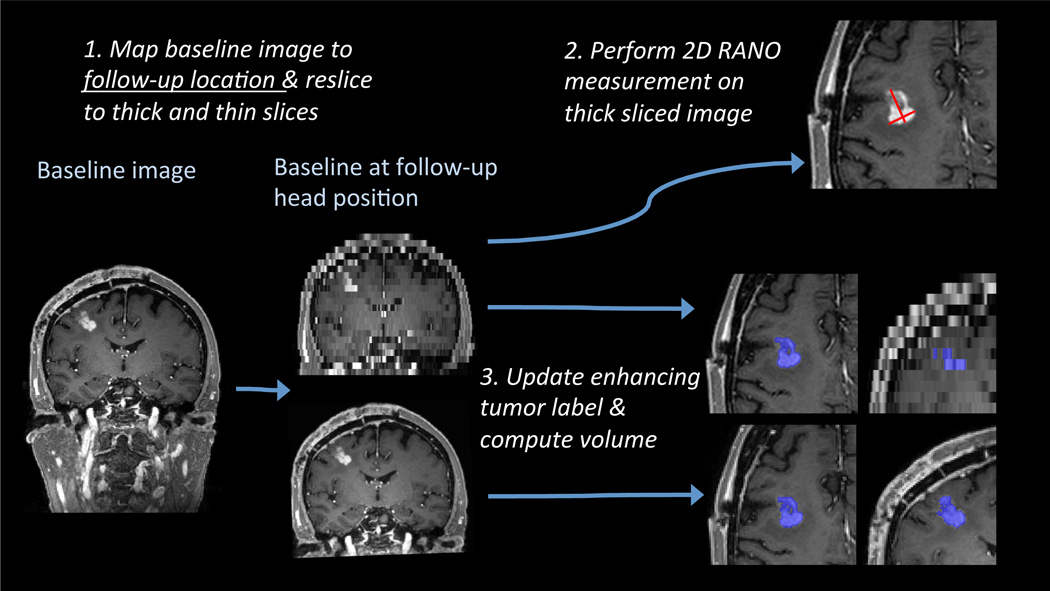
To simulate acquisition of the identical image under different head placements, the baseline MEMPRAGE of each subject was reoriented (mapped) to a follow-up position using the transformations T_ij, and resliced to typical clinical 5mm thick axial slices and 0.43mm within plane resolution (Figure 2 top). We emphasize that for each subject the same image data was resliced into different realistic orientations defined by the patient’s head in the scanner in each of the subsequent 5–7 imaging sessions. The mapping and reslicing was performed in a single step via cubic B-spline interpolation [10] to minimize interpolation artifacts (such as smoothing caused by standard tri-linear interpolation).

Fig. 2.

Methods flow chart: First the baseline MEMPRAGE gets mapped to a follow-up location and resliced to 5mm and 1mm slices. The 2D RANO measure is performed manually only on the 5mm sliced intensity image, the 3D volume analysis (automatic label update and volume computation) is performed on both the 5mm and 1mm sliced images.

Finally, the maximal perpendicular diameters of the enhancing tumor were drawn on the resliced images by two raters, a neuroradiologist and a neuro-oncologist, following the RANO[11] criteria (see Figure 2 top right). Both raters routinely perform these RANO measurements in clinical settings. Raters were aware of the study design (no anatomical changes) and aimed at producing consistent measurements.

3.2 3D Volume Estimates

To analyze variability of 3D volume estimates, we manually segmented enhancing tumor regions in the baseline image for each patient. The resulting binary labels and the baseline MEMPRAGE images were then mapped to the follow-up positions (using the existing T_ij) with cubic interpolation for the MEMPRAGE and nearest neighbor interpolation for the label images. In order to study the effect of slice thickness on the volume measures both the MEMPRAGE and the label image were resliced to thick slices (5mm and 0.43mm within plane, same as in the 2D RANO study) and additionally to thin slices (1mm isotropic) (Figure 2 bottom). Finally we employed an automatic nonparametric classifier to fine-tune the mapped labels to better match the intensities of the corresponding mapped MEMPRAGE images for each time point. Manual inspection showed that this procedure significantly improves the initial coarse tumor segmentation provided by the re-slicing and nearest neighbor interpolation, especially at the tumor boundary (see Figure 3 for an example). Note, that we do not simulate within or across rater variability that can be associated with manual 3D segmentations of a clinical workflow. Real test-retest data relying on individual manual segmentations in all time points can be expected to include imaging noise as well as within- and cross-rater measurement noise, and thus demonstrate even larger variability.

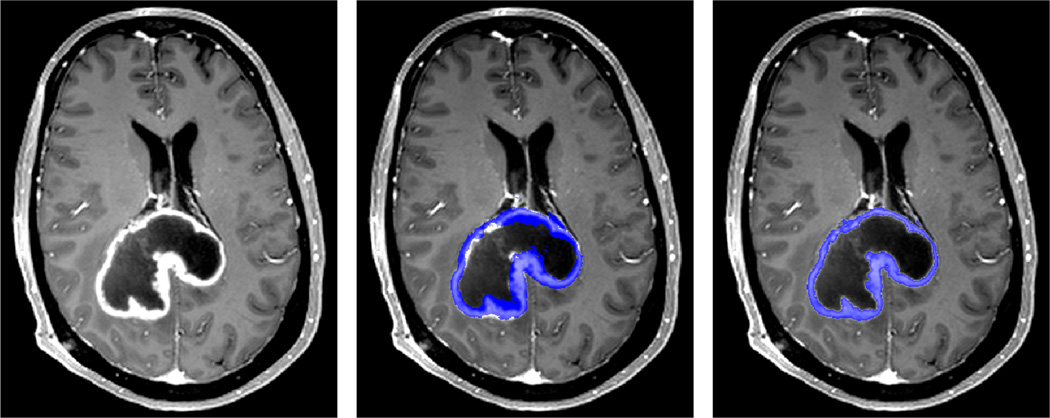
Fig. 3.

Axial slice showing enhancing tumor (left). The corresponding coarse label of enhancing region (middle, blue) is improved by our automated classification (right, blue).

3.3 Statistics

The root mean squared error (RMSE) was used to compute the difference of the n measured values y_t with respect to their median ŷ:

$$RMSE=\sqrt{\frac{{\sum }_{t=1}^n{(y_t-ŷ)}^2}{n}}$$ (1)

We computed RMSE for each subject and rater independently and report the average RMSE (within rater and overall).

We quantified agreement of measurements across raters with Lin’s concordance correlation coefficient [5] and employed the non-parametric Wilcoxon’s signed rank test [12] to assess measurement bias between the raters. The intraclass correlation coefficient (ICC) [13] was used to estimate within rater reliability. Furthermore, as a robust estimate of measurement noise, we report the median largest percent increase (MLPI) and decrease (MLPD) by computing the median across all subjects of the largest percent increase (and decrease) within subject.

4 Results

4.1 2D RANO Measurements

The contrast enhancing area (diameter product, see RANO) was measured by two raters independently. Tumor area measurements ranged from 2cm² to 16cm² across patients (average 8cm²).

Despite the lack of any real tumor change (the identical image was only resliced differently) the variability of the product of the diameters was large across the simulated visits. Using the median measurement of each rater within each subject as a robust estimate for true tumor size (as defined by that rater) we obtained a root mean squared error of 22% across all measures (18% and 25% for the individual raters respectively). Note, this is a lower bound as all errors were computed with respect to each rater’s median, rather than a fixed tumor size across both raters. We also estimated the intraclass correlation coefficient [13] for each rater independently and obtained ICC₁ = 0.92 (confidence interval CI at level 0.05: [0.81, 0.98]) and ICC₂ = 0.93 (CI: [0.84, 0.98]).

Next we analyzed the between-rater reliability. We obtained a correlation of 0.89 between the two raters and Lin’s concordance correlation coefficient [5] of 0.83. The median difference between the two raters was 0.57cm² and the mean difference 1.49cm². Although the difference is small, a two-sided paired test on the median is significant (p < 0.002 in Wilcoxon’s signed rank test [12]), showing that one rater tends to produce larger estimates than the other.

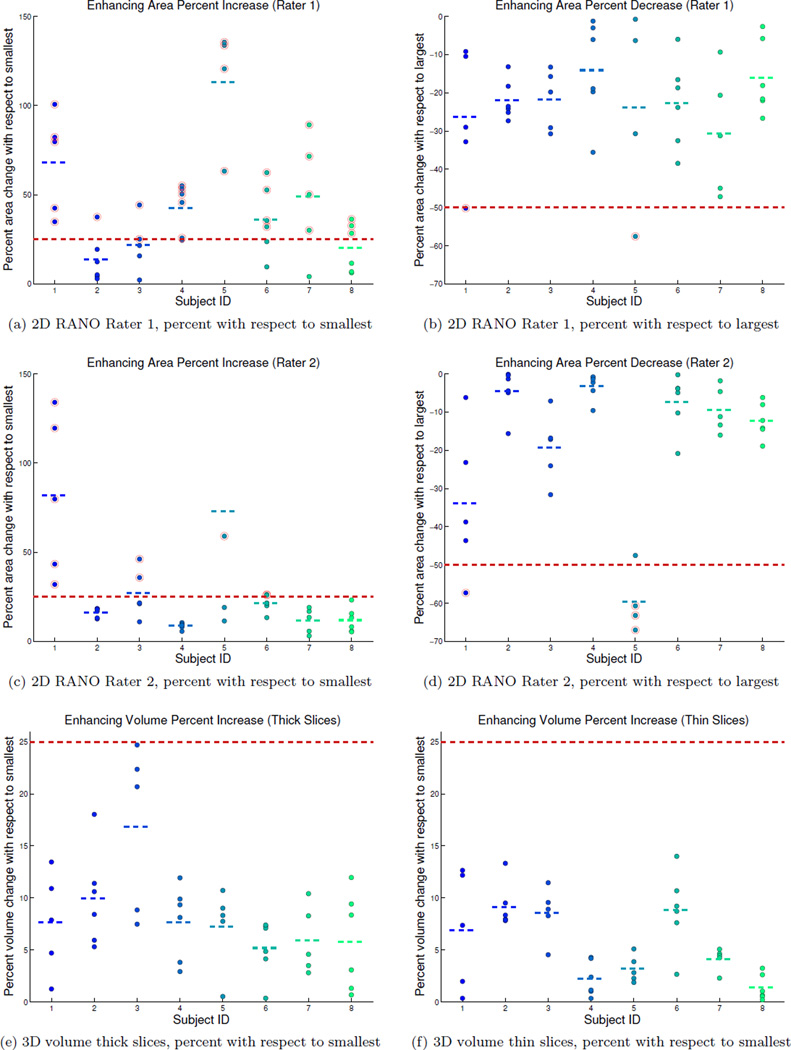
Given that the RANO guidelines define “progression” by at least 25% increase of the 2D area estimate compared to the smallest measurement, it makes sense to compute percent change with respect to the minimum. Plots 4a and 4c show the percent increase of the repeated measures with respect to the smallest for each subject. For rater 1, all 8 patients would have been incorrectly diagnosed as having progressive disease at at least one measurement and would be removed from a potential clinical trial without real tumor changes (4 patients for rater 2). The maximal percent increase across all subjects was 136% and 203% and the median largest percent increase 59% and 25% for rater 1 and 2 respectively.

A diagnosis of “partial response” requires more than 50% decrease compared to the baseline measurement. Depending on the order of the time points in this simulated test, two patients fulfilled this requirement for both raters (see plots 4b and 4d depicting percent decrease with respect to the largest measurement). The maximal percent decrease was 58% and 67% and the median largest percent decrease 37% and 20% respectively.

4.2 3D Volume Estimates

Enhancing tumor volume estimates across all subjects ranged from 2.7ml to 37.5ml with an average of 15.9ml (computed from the manual ROI in the isotropic baseline images).

4.2.1 Thick Slices

Using the median volume within each subject as a robust estimate for true tumor size we obtained a root mean squared error of 4.8% across all measures. We also estimated the intraclass correlation coefficient [13] as ICC_υ = 0.991 (CI [0.976, 0.997] at level 0.05). Figure 4e shows the percent volumes of each of the tumor segmentations relative to the smallest volume estimate in each subject. As can be seen, the 3D volume analysis reduces the variance of the procedure relative to 2D area (Figures 4a and 4c), but apparent volume changes of above 20% are still seen with a median largest percent increase of 12%.

Fig. 4.

Apparent percent change (actual tumor change is 0%) of repeated measures per subject (IDs 1–8). Plots (a,c) show percent increase of contrast enhaning area (2D RANO) computed with respect to the smallest measure in each subject and (b,d) percent area decrease with respect to the largest measure (for rater 1 top row, and rater 2 middle row). Short dashed lines show the mean for each subject. Thick dashed red lines indicate the 25% increase of progressive disease (a,c,e,f), and 50% decrease of a partial response (b,d). Measurements above (or below) these thresholds are circled in red. All subjects would be “progressing” in (a) and 4 subjects in (c) (plot (c) is clipped at 150%, maximum increase in subject 5 is 203%). Plots (e,f) show apparent percent increase in 3D volume with respect to the smallest measure for thick (e) and thin (f) image slices.

4.2.2 Thin Slices

To analyze reliability improvements when switching to thinner slices, we used the same procedure as above, but this time reslice the baseline multi-echo MPRAGE and enhancing ROI label to the follow-up positions using 1mm isotropic voxels. Taking the median volume within each subject as a robust estimate for true tumor size we obtained a root mean squared error of 3.2% across all measures. We also estimated the intraclass correlation coefficient [13] as ICC_υ = 0.998 (CI [0.996, 0.999] at level 0.05). Figure 4f shows the percent volumes of each of the tumor segmentations relative to the smallest estimate using the thin slice data. As can be seen, working with thinner slices reduces the variance of the procedure relative to the 3D thick sliced volume (Figure 4e) and the 2D area (Figures 4a, 4c). Apparent volume changes of above 10% are still seen with a median largest percent increase of 8%.

Note that the 3D volume experiments can be considered a lower bound on the reliability that these volume measurements can achieve as they represent the noise- and artifact-free case: imaging noise and motion artifacts that occur in longitudinal patient visits, as well as inter- and intra-rater discrepancies will only increase the noise. Table 1 shows an overview of the reliability for the 2D RANO and 3D volume measures.

Table 1.

Statistics Overview: root mean squared error (RMSE), intraclass correlation coefficient (ICC) and median largest percent increase (MLPI).

	2D RANO	3D Vol Thick	3D Vol Thin
RMSE	22%	4.8%	3.2%
ICC	0.93	0.991	0.998
MLPI	59%, 25%	12%	8%

5 Discussion

With the 2D RANO measurement, intra-observer reliability of the 2D area measure has been reported to be usually very high (correlation > 0.98 with narrow confidence intervals) [8]. The low concordance 0.83 between the two raters here indicates that in some cases different tumor regions were measured. Specifically, situations with enhancing rings around a necrotic core or cyst tend to complicate the selection of the largest nodule. Often slices at the superior or inferior tumor boundary are selected for the RANO measurement, because their tangential location warrants a large intersection with enhancing tumor tissue (see, e.g., Figure 1). However, due to their location at the boundary, these slices are particularly prone to large variability with only small variation of slice orientation and position. Measurements of two raters are certainly not sufficient to robustly estimate inter-observer reliability.

Even for the same rater it can be difficult to follow a specific region over time: a different nodule than was initially measured as the target region may appear larger at a follow-up head position. Within rater reliability was low with ICC’s of 0.92 and 0.93 and a median largest percent increases with respect to the smallest measure of 59% and 25%. The large variability of the RANO 2D area analysis highlights the need for improved response assessment criteria. In particular, basing the diagnosis of disease progression on a comparison with the smallest tumor size measure is problematic, as a single incorrect small measure can inflict a wrong diagnosis. 25% of the smallest measure is naturally even smaller and can easily fall below the reliability level. Additionally, defining progression as soon as a new lesion becomes measurable [11] can also be problematic as smaller lesions easily shift in and out visibility due to changes in slice position.

Incorrectly removing subjects from drug trials because of a wrong diagnosis will decrease statistical power and may bias results, considering that subjects with small tumors, larger resections, or better initial response to anti-angiogenic therapies have a higher probability to be incorrectly removed. In addition, with a short median survival time of only 9–15 months following standard therapies, an incorrect assessment of progression can cause significant psychological harm for the patient and family. Until response criteria are based on more reliable acquisition protocols, such as automated slice prescription to a previous visit, or high-resolution isotropic 3D imaging, we recommend a revision of the current RANO recommendations to account for measurement noise. For example, basing comparisons on the average of the three smallest measurements (or the last three visits, or multiple baseline) instead of the single smallest measurement, should significantly reduce diagnostic error.

Our results comparing the 2D RANO with 3D volume measures are in concordance with the results on low-grade tumors [9], and indicate that volume measures are more robust and reliable in the presence of head position changes, presumably due to the additional information obtained by analyzing the full shape of the enhancing tumor as opposed to the area measures that are dependent on only a single 2D slice. Nevertheless, even the volumetric analysis inherits severe reliability issues caused by positional changes. We show that thin (1mm) slices increase reliability over the clinical thick (5mm) slices in spite of the 1mm isotropic image having lower within plane resolution. It can be expected that performing volume measurements in the same space as baseline, after registration of follow-up images, will further increase reliability, as partial volume effects will be reduced.

For these reasons, we recommend the acquisition of 1mm isotropic images that can be accurately registered to a previous scan off-line via robust alignment procedures that are specifically targeted at tumor applications, e.g. [7]. This allows a more accurate and reliable volume analysis as well as quantification of local longitudinal changes. Acquisition of a 1mm isotropic MPRAGE image can be accelerated to less than 4min and does not have a significant impact on scanner and patient time requirements. Furthermore, in spite of their current limitations, we recommend the use of supervised AutoAlign procedures on the scanner to improve slice alignment across sessions, and to correct for motion between sequences within a scan session.

Our findings, that await confirmation in real test-retest studies on larger data sets, highlight the importance of defining guidelines that make use of all the available 3D image information and acquisition protocols. Switching to 1mm isotropic images together with a switch to volumetric analysis, instead of the 2D perpendicular diameter, can be expected to significantly reduce the sensitivity to scanning conditions. In a busy clinical practice volumetric measurements may still be logistically challenging until automatic segmentation programs improve. In those settings, using an average measurement of two or three scans instead of comparing to the nadir area should increase reliability of the 2D measurements. To ensure the same region is followed longitudinally, measurements should be performed, if possible, on 1mm isotropic images co-registered to the baseline scan.