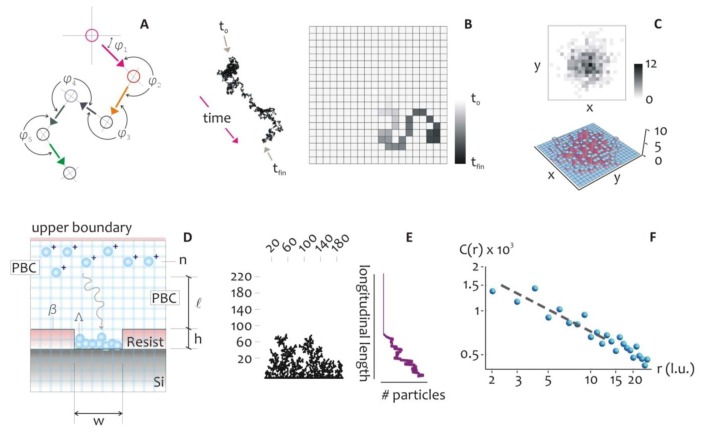
Figure 2.

We used a Diffusion Limited Aggregation (DLA) model to simulate the electroless deposition of silver ions into supra-molecular structures. In the model, the trajectory of the particles can be described by a random walk, as to resemble a Brownian motion (A). The motion of a particle can be simulated in a regular lattice, where the smallest block of the lattice is called the lattice unit, that represents the spatial resolution of the simulation (that is, a pixel) (B). The distribution of displacements of a particle may be described using a Gaussian density function (C). This concept was used to simulate the deposition of metal ions in a patterned silicon substrate, (D), where a sufficiently large number n of particles is released in the system and let free to evolve. Using this scheme, an aggregate can be formed as in (E), where the multi branched arrangement of particles recalls the dendrite, fractal nature that electroless grown systems reveal under certain growth conditions. In (F), we report the pair correlation function of a similar numerical aggregate. A pair correlation function describes the change of information content of an aggregate as a function of change in scale and it is typically reported in a log log plot. In the diagram, the y axis represents the correlation function, while the x axis is the distance from the geometrical center of the aggregate expressed in lattice units (pixels). The pair correlation function is therefore related to the probability of finding the center of a particle a given distance from the center of another particle. For short distances, this is related to how the particles are packed together. On calculating the slope of this diagram, the fractal dimension of an aggregate can be derived.