An Investigation of G-Quadruplex Structural Polymorphism in the Human Telomere Using a Combined Approach of Hydrodynamic Bead Modeling and Molecular Dynamics Simulation

Abstract

Guanine-rich oligonucleotides can adopt noncanonical tertiary structures known as G-quadruplexes, which can exist in different forms depending on experimental conditions. High-resolution structural methods, such as X-ray crystallography and NMR spectroscopy, have been of limited usefulness in resolving the inherent structural polymorphism associated with G-quadruplex formation. The lack of, or the ambiguous nature of, currently available high-resolution structural data, in turn, has severely hindered investigations into the nature of these structures and their interactions with small-molecule inhibitors. We have used molecular dynamics in conjunction with hydrodynamic bead modeling to study the structures of the human telomeric G-quadruplex-forming sequences at the atomic level. We demonstrated that molecular dynamics can reproduce experimental hydrodynamic measurements and thus can be a powerful tool in the structural study of existing G-quadruplex sequences or in the prediction of new G-quadruplex structures.

Introduction

In solutions with physiological Na⁺ and K⁺ concentration, single-stranded guanine-rich oligonucleotide sequences can self-assemble and fold into unimolecular G-quadruplexes, noncanonical DNA tertiary structures composed of a four-stranded helical stem and three interconnecting loops.¹ Within the human genome, over 370 000 putative G-quadruplex-forming sequences have been identified and most of these are observed to localize to genomic regions with important cellular functions, such as the telomere, immunoglobulin switch regions, proto-oncogene promoters, and mRNA untranslated regions.^2,3 Many of these sequences are found to be evolutionarily conserved between humans, mice, and rats⁴ suggesting that G-quadruplex structures play important regulatory roles within the cell. The formation of G-quadruplex at the distal 3′ end of the human telomere region,⁵ which contains a single-stranded guanine-rich overhang of approximately 100–200 bases, has been investigated as a potential target for novel small-molecule-based anticancer therapy. Small molecules that stabilize telomeric G-quadruplex structures have been shown to decrease the activity of telomerase in vitro.⁶⁻¹⁰ Since telomerase is activated in more than 90% of all cancers,¹¹ G-quadruplex-based antitelomerase therapy could be an attractive strategy for the development of anticancer therapeutics.

Despite considerable research being devoted to targeting telomeric G-quadruplexes,^8,12−17 the development of small-molecule G-quadruplex-based inhibitors has progressed slowly with only one candidate drug making it to clinical trials.¹⁸ A challenge to the rational design of small molecules that bind specifically to G-quadruplexes is the lack of, or the ambiguous nature of, high-resolution structural data for many putative G-quadruplex-forming sequences. In fact, the hTel22 sequence, AGGGTTAGGGTTAGGGTTAGGG, which is often used as an in vitro model for G-quadruplex formation in the human telomere,^19,20 has been found to exist in many forms depending on experimental conditions and sequence composition (Table 1). In the presence of sodium, it is widely accepted that this sequence folds into an antiparallel “basket” topology¹⁹ which consists of three stacked G-tetrads with one diagonal and two lateral loops. In the presence of potassium, it exists as an ensemble of structures, which includes two mixed “hybrid” topologies (hybrid-1²¹⁻²³ and hybrid-2^23,24), a parallel “propeller” topology,²⁰ and a new antiparallel “basket” topology.^25,26 Hybrid-1 consists of three stacked G-tetrads with a double chain-reversal loop followed by two lateral loops. Hybrid-2 also consists of three stacked G-tetrads but with reversed loop order, two lateral loops followed by a double chain-reversal loop. The parallel “propeller” topology consists of three stacked G-tetrads and three double chain-reversal loops. Lastly, the K⁺ antiparallel “basket” topology consists of two stacked G-tetrads with a diagonal and two lateral loops.

Table 1. G-Quadruplex-Forming Sequences for HYDROPRO Calculations.

sequencea	designationb	topology	type	cations
AGGGTTAGGGTTAGGGTTAGGG	143D	basket	solution	Na+
AGGGTTAGGGTTAGGGTTAGGG	1KF1	propeller	crystal	K+
TTGGGTTAGGGTTAGGGTTAGGGA	2GKU	hybrid-1	solution	K+
AAAGGGTTAGGGTTAGGGTTAGGGAA	2HY9	hybrid-1	solution	K+
TAGGGTTAGGGTTAGGGTTAGGG	2JSM	hybrid-1	solution	K+
TTAGGGTTAGGGTTAGGGTTAGGGTT	2JPZ	hybrid-2	solution	K+
TAGGGTTAGGGTTAGGGTTAGGGTT	2JSL	hybrid-2	solution	K+
GGGTTAGGGTTAGGGTTAGGGT	2KF8	basket	solution	K+
AGGGTTAGGGTTAGGGTTAGGGT	2KKA-G	basket	solution	K+
AGGGTTAGGGTTAIGGTTAGGGT	2KKA-I	basket	solution	K+

^aG-quartet stem residues (bold) and flanking residues (italic). Noncanonical residues (underline).

^bProtein Data Bank code (www.pdb.org).

The inherent structural polymorphism associated with G-quadruplex formation has severely hindered investigations of G-quadruplex structures and their formation. As a consequence, steps are usually taken to artificially reduce the structural polymorphism with the goal of enrichment of one species for NMR structure elucidation.^27,28 Sequence modification, as seen with human telomere sequence, is one common approach. The reported sequence variants for the human telomere sequence (Table 1) demonstrate how small changes with respect to the flanking bases can result in dramatically different dominant topologies. While each sequence contains the identical G-quadruplex-forming core GGGTTAGGGTTAGGGTTAGGG, the flanking bases differ from the hTel22 sequence (5′-A-core-3′), which contains a mixture of G-quadruplex structures, compared to the hybrid-1 dominant sequences (2GKU, 5′-TT-core-A-3′; 2HY9, 5′-AAA-core-AA-3′; 2JSM, 5′-TA-core-3′),²¹⁻²³ the hybrid-2 dominant sequences (2JPZ, 5′-TTA-core-TT-3′; 2JSL, 5′-TA-core-TT-3′),^23,24 and the antiparallel dominant sequences (2KF8, 5′-core-T-3′; 2KKA, 5′-A-core-T-3′).^25,26 In addition to changes in the flanking bases, G-quadruplex-forming sequences can also be truncated or elongated. Often, sequence modifications also involve the incorporation of noncanonical bases, as is the case with the 2KKA sequence which contains an inosine substitution for guanine. A list of G-quadruplex modifying constituents and their effects on G-quadruplex formation can be found in a recent review.²⁹

Aside from sequence modification, another common approach to reduce the structural polymorphism is by changing the solution conditions. The presence of biological molecules³⁰ (e.g., sugar, proteins), cosolvents (e.g., acetonitrile, PEG),³¹⁻³³ the use of divalent versus monovalent cations,^34,35 and cation concentration³⁶⁻³⁸ all play a major role in determining G-quadruplex stability. The parallel topology of hTel22 clearly illustrates the effect of experimental conditions on G-quadruplex formation. This topology was first reported in potassium conditions as a crystal structure.²⁰ It was later determined that this is not the predominant topology in solution^33,39,40 and accounts for only about 14% of the total G-quadruplex structures.³³ However, under the effect of dehydration³² or in the presence of PEG³³ (both factors present in the crystallization conditions), the parallel topology is enriched to become the predominant form. In fact, as proof of this principle, a recently reported NMR solution structure⁴¹ for hTel22 in 40% poly(ethylene glycol) (PEG 200) was similar to the previously reported crystal structure.

The unintended consequence of sequence modification or alteration of experimental conditions is that such an approach can result in an unpredictable perturbation of the system and the selection of a topology which may or may not be representative of the original ensemble of topologies.⁴² However, these approaches for the artificial reduction of the structural polymorphism are used because of the limitations of traditional biophysical methods with regard to elucidating G-quadruplex structure. Low-resolution spectroscopy methods, such as circular dichroism or UV–vis spectroscopy, usually cannot distinguish between the different topologies within the ensemble,^38,43 while high-resolution structural methods, such as NMR spectroscopy and X-ray crystallography, are often of limited utility when it comes to resolving the structural polymorphism of G-quadruplexes. As observed with hTel22, a definitive structure cannot be obtained by NMR spectroscopy because this sequence exists as a mixture of multiple G-quadruplex species in solution.¹ The alternative method, X-ray crystallography, may not be appropriate either, as, under dehydrating crystallization conditions, this sequence adopts a topology that may not be representative of the ensemble in solution³³ or in vivo.⁴⁰ This has a significant effect on what structure or structures can be claimed as “biologically relevant”. Thus, there is a need for new experimental approaches that can explore the conformational space surrounding the G-quadruplex topologies without significantly disrupting or perturbing the system.

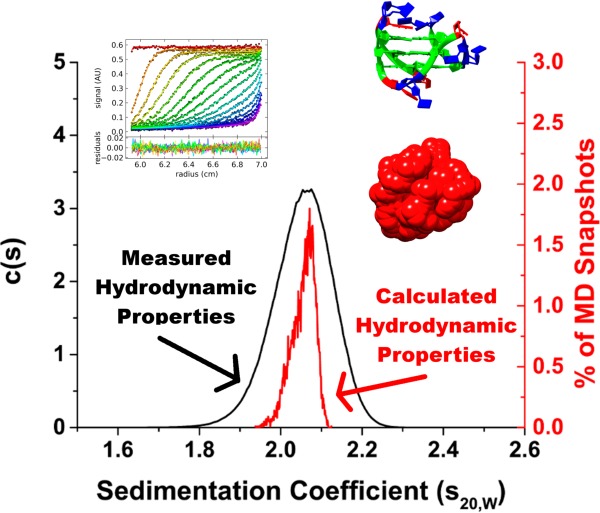
We propose an alternative approach for the unperturbed investigation of G-quadruplex structures, hydrodynamic bead modeling (HBM). HBM has emerged as a useful tool for studying biological macromolecules and their complexes for which high-resolution structural data are either unavailable or ambiguous.⁴⁴ HBM has been used, in a limited scope, to study G-quadruplex structures. In 1999, Niermann et al. used HBM to calculate the rotational and translational diffusion coefficients for the Watson–Crick double helical B-DNA, the single-stranded duplex “hairpin”, and the tetramolecular G-quadruplex structures.⁴⁵ In 2005, Li et al. employed HBM to demonstrate that the crystal structure of the hTel22 telomere sequence in potassium is not the predominant topology in solution.³⁹ More recently, Petraccone et al. used HBM to study higher-order G-quadruplex formation by the human telomeric sequence (T₂AG₃)_nT₂ (n = 4, 8, 12).⁴⁶⁻⁴⁸ The purpose of the current work is to use hydrodynamic bead modeling in tandem with molecular dynamics (MD) simulations to explore the structural polymorphism of the human telomere G-quadruplex sequence. In particular, we exploited recent advances in computing hardware, which makes it feasible for routine microsecond-time scale simulations through traditional MD methods. Compared to shorter nanosecond simulations, longer simulations are better at sampling conformations while avoiding the bias of the starting structures.⁴⁹ Using MD, we explored the conformational space surrounding the five different folding topologies associated with the human telomere sequence. HBM was used to calculate sedimentation coefficients (s_20,W) and other hydrodynamic properties for “snapshot” structures obtained by MD simulations. Overall, the calculated hydrodynamic values agreed with experimental values obtained via analytical ultracentrifugation (AUC) studies. Clustering of the MD trajectories using s_20,W values revealed the existence of different hydrodynamic substates within the ensemble of structures. Using principal component analysis (PCA) of the MD trajectory, the key motions of the G-quadruplex structures that are responsible for variations observed by hydrodynamic measurements were identified. Grid mapping of water and cations around the DNA also provides valuable insights into the role of hydration and ion binding in hydrodynamic measurements. Lastly, a novel use for HBM is proposed to estimate the number of counterions bound to a particular G-quadruplex structure when accurate information about the size and shape of the DNA is known. This work demonstrates that hydrodynamic bead modeling in conjunction with MD simulations is a powerful technique to study G-quadruplex structures.

Experimental Methods

Molecular Dynamics (MD) Simulation

Molecular models of G-quadruplex structures were obtained from the Protein Data Bank using the PDB IDs in Table 1. For structures containing multiple models, the first model in the file was selected for AMBER MD simulations. Appropriate coordinating ions were added to the stacked G-tetrads of each model, and additional ions were added to neutralize the G-quadruplex structures. The system was solvated in a truncated octahedral box of TIP3P water molecules with 10 Å buffer. The system was heated and equilibrated using the following protocol: (i) minimize water and ions (1000 steps – 500 steepest descents) holding the DNA fixed (50 kcal/mol/Å), (ii) 50 ps MD (heating to 300 K) holding the DNA fixed, (iii) repeat step i, (iv) minimize all atoms (2500 steps – 1000 steepest descents), (v) repeat step ii, (vi) 50 ns MD (T = 300 K) equilibration holding the DNA fixed (50 kcal/mol/Å), and (vii) 50 ns MD to finish the equilibrium period. Production runs of 1 μs after the final equilibration step were carried out to obtain snapshots at 100 ps interval for a total of 10 000 snapshots. Simulations were performed in the isothermal isobaric ensemble (P = 1 atm, T = 300 K) using sander and GPU version of pmemd. Periodic boundary conditions and particle-mesh-Ewald algorithms were used. A 2.0 fs time step was used with bonds involving hydrogen atoms frozen using SHAKE. Analysis of the trajectory was performed using the cpptraj module of the AmberTools 13 Package. Calculations of hydrodynamic properties were done using the program HYDROPRO. All AMBER and HYDROPRO calculations were conducted in part using the resources of the University of Louisville’s research computing group and the Cardinal Research Cluster.

Oligonucleotide Preparation and Annealing

The human telomere G-quadruplex-forming oligonucleotide, dAG₃(T₂AG₃)₃, and its derivatives (Table 1) were purchased from Integrated DNA Technologies (Coralsville, IA). A stock solution (1 mM) of each oligonucleotide was prepared by dissolving the lyophilized DNA in TBAP buffer (10 mM tetrabutylammoniumphosphate monobasic, 1 mM EDTA, pH 7.0). The DNA was quantified using a Nanodrop 2000 instrument (Thermo Scientific, Wilmington, DE). The molar extinction coefficient (ε) for each oligonucleotide was calculated via the nearest-neighbor method. Prior to sedimentation velocity experiments, the DNA samples were diluted in TBAP buffer to an A₂₆₀ value of 0.5, and salt was added to the solution to bring the final concentration of NaCl or KCl to 400 mM. The oligonucleotide samples were annealed in a water bath by heating to 100 °C, holding the sample at temperature for 10 min, and gradually cooling to room temperature overnight.

Analytical Ultracentrifugation (AUC)

AUC was carried out in a Beckman Coulter ProteomeLab XL-A analytical ultracentrifuge (Beckman Coulter Inc., Brea, CA) at 20.0 °C overnight at 50 000 rpm in standard 2 sector cells. Data were analyzed using the program Sedfit (www.sefit.com). The discrete noninteracting species model in Sedfit was used to determine experimental values for s_20,W and D_t20,W for comparison with HYDROPRO. The concentration-dependent distributions of sedimenting species were calculated using the c(s) continuous distribution model using measured values for buffer density and viscosity. Buffer density was determined on a Mettler/Paar Calculating Density Meter DMA 55A at 20.0 °C, and viscosity was measured using an Anton Parr AMVn Automated Microviscometer. For the calculation of frictional ratio, 0.55 mL/g was used for partial specific volume and 0.3 g/g was assumed for the amount of water bound.

Calibration of HYDROPRO Parameters

The atomic element radius (AER), or bead size, of the primary HYDROPRO hydrodynamic model was calibrated to the Stokes radius of the DNA obtained by AUC. In HYDROPRO, the Stokes radius is reported as the equivalent translational radius, defined as the radius of the sphere with equivalent translational diffusion coefficient value. The calculated values were taken as an average over the number of poses available in the Protein Data Bank. For 143D, 6 poses were deposited in the PDB record. For 2GKU, 12 poses were deposited. For 2HY9, 2JPZ, 2JSL, 2JSM, and 2KF8, 10 poses were deposited. The experimental values were determined as previously described. The calculated values were fitted to the experimental values using a global-fit approach (eq 1) described in the latest HYDROPRO calibration report.⁵⁰

1

The Δ value is the root-mean-square relative difference between the calculated values and the experimental values, with 100Δ representing the percent difference typically used to characterize the goodness of prediction.

Hierarchical Agglomerative Cluster Analysis

Cluster analysis was performed using the cpptraj module of the AmberTools 13 Package. In hierarchical agglomerative clustering, each data point began in its own cluster and the two closest clusters were merged into a new cluster following after one run of the clustering iteration. The clustering process stopped when a certain number of clusters remained. In order to determine the optimum number of clusters, cluster analyses were performed until one to nine clusters remained. For each cluster analysis, ANOVA was employed to calculate the sums of squares. The percent of variance explained by the clustering was determined by dividing the regression sum of squares by the total sum of squares. The cluster number corresponding to the greatest increase in the percent of variance explained was taken as the optimum number of clusters. For instance, if the greatest increase in percent variance occurred when the number of clusters increased from two to three, three was designated the optimum cluster number. Following cluster analysis, the “snapshot” structures from each cluster were extracted for further investigation.

Free Energy Calculation

Free energy calculations were performed using the MMPBSA module of the AmberTools 13 Package. Solvation free energies were estimated with a nonlinear Poisson–Boltzmann electrostatic continuum method with a hydrophobic component from a surface-area-dependent term. The solute dielectric constant was κ = 1. A cubic lattice with linear dimensions ∼50% larger than the longest dimension was applied with 0.25 Å grid spacing; potentials at the boundaries of the finite-difference lattice were set to a sum of Debye–Huckel potentials. Salt effects were set to be 0.400 M, which corresponded to the salt concentration of sodium and potassium used in the sedimentation velocity experiments. To estimate the nonpolar contributions to solvation, ΔG_nonpolar, the solvent accessible surface area (SASA) algorithm of Sanner was used in a parametrization where ΔG_nonpolar = γ(SASA) + β, where γ = 0.00542 kcal/Ų and β = 0.92 kcal/mol.

Principal Component Analysis (PCA)

PCA was performed using the cpptraj module of the AmberTools 13 Package. The eigenvectors and eigenvalues were calculated from the diagonalization of the covariance matrix which contained the atomic positional fluctuation, about the average structures, in Cartesian coordinate spaces for all three coordinate axes. The covariance matrix is a 3N × 3N matrix with 3N – 6 eigenvectors possible, where N is the number of atoms in the system.⁵¹ The eigenvectors describe the nature of the fluctuation, while the eigenvalues describe the contribution of each eigenvector to the overall atomic fluctuation. The results were the partition of the atomic positional fluctuations reported in the previous section into individual components in a way that all components are orthogonal to each other and that the first component accounts for the most variance possible and that each subsequent component, in turn, accounts for the highest variance possible while remaining orthogonal to the preceding components.

Radial Distribution Functions (RDFs) and Grid Mapping

RDF and grid mapping were performed using the cpptraj module of the AmberTools 13 Package. The number of water molecules bound to the G-quadruplex structure was calculated by integrating the RDF function up to the first minimum, which represents the boundary of the primary hydration shell. Prior to grid mapping, the trajectory was prepared using the autoimage command. The structures were RMS fit to the bases of the G-tetrads. Grid mappings of water and cation distributions were calculated by binning atom positions at 100 ps intervals into 0.5 × 0.5 × 0.5 ų grids over 1 μs duration of the trajectories. In other words, the value of each grid element represents the number of times the coordinates of the center of a particular atom of interest (i.e., water oxygen) were within the 0.5 × 0.5 × 0.5 ų represented by that particular grid element. For 10 000 frames, the expected number of waters per grid element, assuming bulk water density (55.5 M), was 42. The reference density was 6 M for sodium and 4 M for potassium, which represents the solubility of NaCl and KCl in water, respectively. This corresponded to an expected 4.5 sodium atoms and 3.0 potassium atoms per grid element.

Results and Discussion

Molecular Dynamics Simulations of Telomeric G-Quadruplex Structures

The aim of this research was the detailed evaluation and parametrization of HBM in the study of G-quadruplex structural polymorphism. To that end, MD simulations were performed to sample the conformational spaces around the human telomere G-quadruplex structures and to produce “snapshot” structures for subsequent hydrodynamic calculations. Simulations were performed on 10 different G-quadruplex structures representing the five folding topologies (Table 1): the antiparallel “basket” in sodium, the parallel “propeller”, the mixed “hybrid-1”, the mixed “hybrid-2”, and the antiparallel “basket” in potassium. For the parallel “propeller” topology, the crystal structure originally reported by Parkinson et al.²⁰ was used. In addition, simulations were performed on two separate models of the 2KKA structure.²⁶ The 2KKA-I model, which contains an inosine substitution for guanine at position 14, is the model deposited in the PDB database. 2KKA-G is a model created by changing the inosine residue back to guanine in order to study the effect of inosine substitution on G-quadruplex formation.

The best-fit root-mean-square deviations (RMSDs) over the full 1 μs of the MD trajectories for the G-quadruplexes indicated that the stem structures are rigid and the loop and flanking structures are more flexible (Figure 1). The stem of two or three stacked G-tetrads, held together by Hoogsteen hydrogen bonds and supported by the π–π stacking interaction between adjacent G-tetrads and the electrostatic interaction between the centrally coordinated cations, was the more rigid structural feature (average RMSD of 1.0 Å). The lower RMSD values that were observed for just the guanine bases alone (average RMSD of 0.5 Å) compared to the complete stem can be attributed to the more flexible phosphate backbone. Compared to just the stem alone, the RMSD for the G-quadruplex as a whole was much higher, with RMSD values as high as 4.5 Å. To highlight the mobility of different structural components in the G-quadruplex structures, the atomic positional fluctuations were calculated on a per-atom and per-residue basis (Supporting Information, Figures S1 and S2) and mapped to representative structures from the MD trajectories (Figure 2). The fluctuation calculation is a better indicator of mobility, whereas the RMSD calculation, which measures the deviation from a reference set of coordinates, is a better indicator of individual substates. The stacked G-tetrad stems were observed to remain remarkably rigid during the course of the simulation (Figure 2, colored red and orange) with an average positional fluctuation of about 0.5 Å (Supporting Information, Figures S1 and S2). This observation agreed with previously reported MD results⁵² and helps explain the stability of these structures in vitro.^42,53,54 In contrast to the rigid stems, the loop and flanking bases were found to be more flexible (Figure 2, colored yellow and green). The thymine loop residues were observed to be more mobile than the adenine loop residues, which have been previously shown to have possible stacking interactions with the G-tetrad stem.^52,55 In addition, different degrees of fluctuation were observed for different loop types. The diagonal loops, which transverse the G-tetrad and are more likely to stack with the G-tetrad bases, appeared more rigid (Figure 2A, H, and I) compared to the chain-reversal loops (Figure 2B–G). These findings regarding loop dynamics have significant implications for ligand recognition, as it is theorized that interaction with loop and flanking bases contributes to a ligand’s G-quadruplex selectivity.

Figure 1.

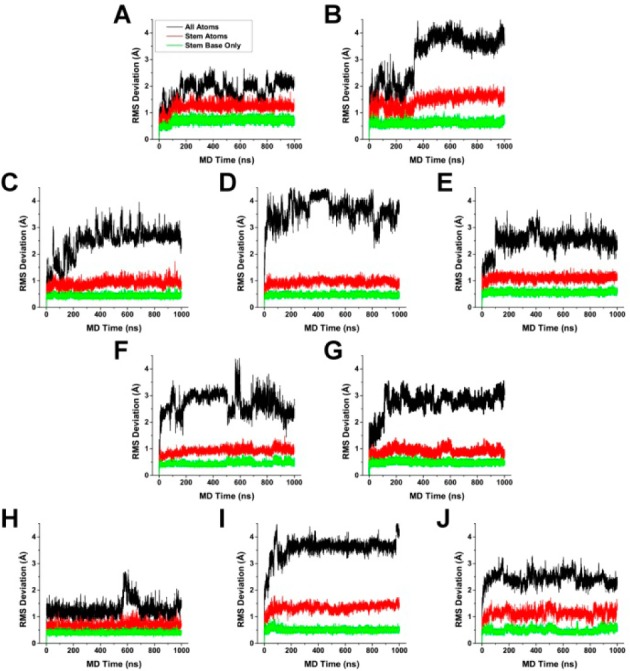
Root mean square deviations with fitting, compared to the first frame, for 143D (A), 1KF1 (B), 2GKU (C), 2HY9 (D), 2JSM (E), 2JPZ (F), 2JSL (G), 2KF8 (H), 2KKA-G (I), and 2KKA-I (J). RMSD calculations were carried out for all non-hydrogen atoms in the G-quadruplex structures (black), in the stacked G-tetrads only (red), and only for G-tetrad guanine bases excluding sugars and phosphate groups (green).

Figure 2.

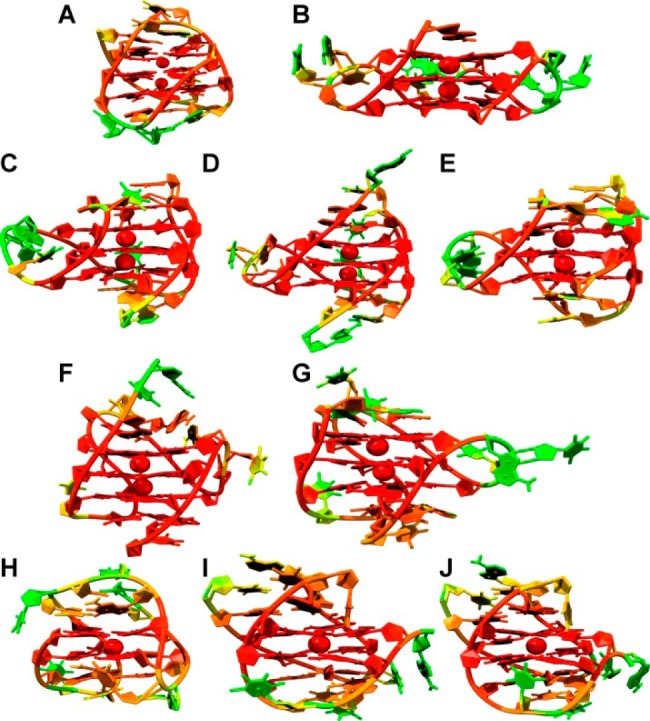
Representative structures from MD trajectories for 143D (A), 1KF1 (B), 2GKU (C), 2HY9 (D), 2JSM (E), 2JPZ (F), 2JSL (G), 2KF8 (H), 2KKA-G (I), and 2KKA-I (J). Residues and atoms are colored by atomic fluctuation units calculated by the AMBER cpptraj module with the color gradient progressing from low fluctuation values to high fluctuation values (red to green, respectively).

Determination of Hydrodynamic Values by Sedimentation Velocity Experiments

MD simulations provided a detailed picture of the G-quadruplex structures in silico. Sedimentation velocity experiments were carried out by AUC to obtain experimental information about the G-quadruplex structures. The 2KKA-I sequence was excluded because of the inosine substitution in order to limit experimental measurements to sequences containing only canonical bases. AUC experiments were performed for the unsubstituted 2KKA-G sequence, which served as an experimental reference for both the 2KKA-G and 2KKA-I MD models. As the data will show, the calculated hydrodynamic values for the 2KKA-I model agreed with the experimental values for the 2KKA-G sequence, suggesting that the inosine substitution did not substantially alter the hydrodynamic behavior of the 2KKA-G sequence in solution. Sedimenting mixtures of polyelectrolytes often exhibit nonideal behaviors due to the electrostatic interaction between different charged components, resulting in smaller measured molecular weights and sedimentation coefficients.⁵⁶ To reduce the effect of nonideality, AUC experiments were carried out in high salt (400 mM NaCl/KCl) buffers to “swamp out” the electrostatic interactions. The distributions of sedimenting species are shown in Figure 3 (black lines). The Stokes radius (a_T), molecular weight (MW), and frictional ratios (f/f₀) were calculated from the diffusion (D_t20,W) and sedimentation coefficients (s_20,W) (Table 2). The frictional ratio is a dimensionless value comparing the observed translational diffusion coefficient of a macromolecule with the translational diffusion coefficient of an equivalent sphere of the same molecular weight with the higher frictional ratios being indicative of a more asymmetric and less spherical shape.^57,58 The value for f is determined from the experimental measurement of D_t20,W using eq 2:

2

where R is the gas constant and N_A is Avogrado’s number. The value for f₀ is determined from the molecular weight using eq 3:

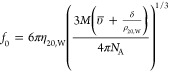3

where η_20,W is the viscosity of water at 20 °C, υ̅ is the partial specific volume, δ is a uniform expansion factor to account for hydration, ρ_20,W is the density of water at 20 °C, and M is the molecular weight determined by the Svedberg equation (eq 4):

4

Figure 3.

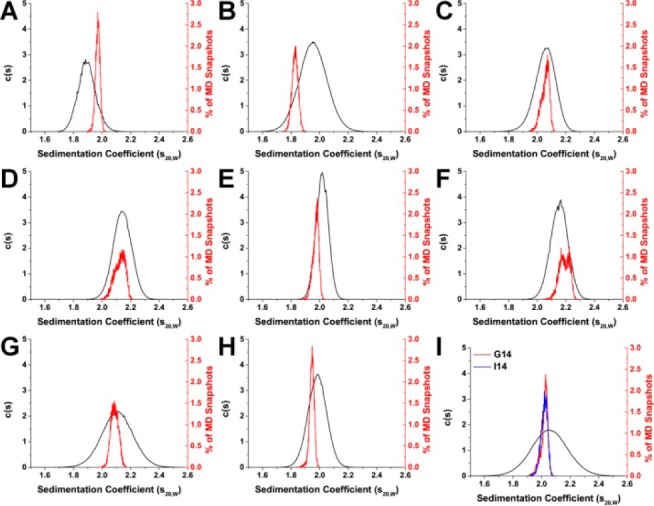
Comparison of experimentally determined and HYDROPRO calculated sedimentation coefficient distributions for 143D (A), 1KF1 (B), 2GKU (C), 2HY9 (D), 2JSM (E), 2JPZ (F), 2JSL (G), 2KF8 (H), and 2KKA (2KKA-G, red; 2KKA-I, blue) (I). For each G-quadruplex structure, sedimentation coefficients (s_20,W) were determined experimentally by AUC (black) and calculated from MD “snapshots” using HYDROPRO (red and blue).

Table 2. Hydrodynamic Values Determined by Sedimentation Velocity Experiments.

G-quadruplex	s20,Wa,b	Dt20,Wa,b	aTb,c	MWd	f/f0e
143D	1.90	1.42	1.50	7199.97	1.10
1KF1	1.97	1.45	1.48	7330.24	1.07
2GKU	2.05	1.45	1.48	7644.45	1.06
2HY9	2.14	1.44	1.49	8039.62	1.05
2JSM	2.02	1.61	1.33	6779.45	1.00
2JPZ	2.15	1.45	1.48	8049.02	1.05
2JSL	2.11	1.41	1.52	8113.66	1.07
2KF8	1.98	1.54	1.39	6975.38	1.03
2KKA-G	2.06	1.58	1.35	7021.38	1.02

^as_20,W and D_t20,W were calculated from sedimentation velocity data using the discrete noninteracting species model of Sedfit.

^bs_20,W expressed in units of 10^–13 s, D_t20,W expressed in units of 10^–6 cm²/s, a_T (Stokes radius) expressed in units of 10^–7 cm.

^ca_T calculated from D_t20,W, solvent viscosity, and temperature.

^dMW is calculated from D_t20,W, solvent density, temperature, and 0.55 mL/g value for partial specific gravity.

^ef/f₀ calculated using 0.3 g/g water bound and 0.55 mL/g value for partial specific gravity.

From these equations, it becomes apparent that the frictional ratio of a macromolecule is dependent on its shape, flexibility, and the amount of hydration associated. In the current work, the amount of associated hydration or δ was assumed to be 0.3 g of water/g of G-quadruplex. For nucleic acids, a value of 0.3–0.35 g/g is typically used, although this parameter can be quite difficult to determine with accuracy.⁵⁹

For each of these sequences, the G-quadruplex structures sedimented as one species (Figure 3), including the hTel22 sequence in potassium and the 2KKA-G sequence, which are known to exist as a mixture of multiple G-quadruplex species.^26,27 The inability of AUC to resolve the existence of different G-quadruplex species in solution can be attributed to the low-resolution nature of the technique. Overall, the G-quadruplex structures formed from different telomeric sequences all assumed similar spherical shapes (f/f₀ = 1.00–1.10). The G-quadruplex structures formed by the hTel22 sequence in sodium (143D) sedimented at a lower rate (s_20,W = 1.90) than G-quadruplex structures in potassium (1KF1) (s_20,W = 1.97), which indicated the sodium form is less compact than the potassium form. Since the sequences are identical in both cases, the difference in sedimentation might be attributed to a change in shape. In fact, the sodium form appeared more elongated (f/f₀ = 1.10) when compared to the potassium form (f/f₀ = 1.07). It is important to note, however, that the difference between the two sequences might not be distinguishable, as it falls within the precision limit of 5% for the experimental technique. For the 2JSM, 2KF8, and 2KKA-G sequences, the changes in sedimentation were also attributed to differences in shape. These sequences have lower mass compared to the hTel22 sequence but are more compact in shape (f/f₀ = 1.00–1.03) and thus sedimented at a higher rate (s_20,W = 1.98–2.06). The differences in frictional ratios of these sequences compared to the 1KF1 sequence were distinguishable, as these differences are greater than the 5% precision limit of the experimental technique. In contrast, the changes in sedimentation for the 2GKU, 2HY9, 2JPZ, and 2JSL sequences compared to the hTel22 sequence can be attributed mainly to a difference in sequence sizes. These sequences appeared to be of similar shape or more compact (f/f₀ = 1.05–1.07) yet sedimented at a higher rate (s_20,W = 2.02–2.15) due to the increased sequence molecular weight. Taken together, these findings indicated that AUC can be informative when used to study G-quadruplex structures.

Calculation of Hydrodynamic Properties Using the Program HYDROPRO

To determine if the in silico models can reproduce the hydrodynamic values observed experimentally, HYDROPRO⁵⁰ was used to calculate the hydrodynamic values (i.e., s_20,W, D_t20W) for each “snapshot” structure obtained from MD simulations. Prior to calculating the hydrodynamic properties, the optimum size of the beads in the primary hydrodynamic model was determined using the procedure previously described.⁵⁰ In brief, the size of the beads (termed the atomic element radius or AER in the HYDROPRO input file) was varied and the AER that yielded the smallest difference between Stokes radius calculated by HYDROPRO (a_T) and the Stokes radius determined by AUC experiments was accepted as the optimum bead size (Table 3 and Supporting Information, Figure S3). For the atomic-level model, where each non-hydrogen atom is replaced with the beads, the physical meaning of AER can be thought of as the radius of a typical non-hydrogen atom plus a uniform expansion to account for hydration. For the residue-level calculations, where each residue (or nucleotide) is replaced with a bead, the physical meaning of AER is the size of the nucleotide plus a uniform expansion to account for hydration. The calibration was done using previously reported NMR structures (PDB ID: 143D, 2GKU, 2HY9, 2JPZ, 2JSL, 2JSM, and 2KF8). All structural poses deposited in the PDB database were used for HYDROPRO calibration. For the first calculation mode where the non-hydrogen atoms were replaced by a collection of overlapping spheres and the hydrodynamic values were calculated using a shell-model methodology,⁶⁰ the best-fit AER was determined to be 2.19 Å (Table 3) with a difference of 2.35% between the predicted hydrodynamic values and the experimental values. For a non-hydrogen atom, the atomic radius is approximately 1.8 Å.⁵⁰ The determined best-fit AER suggests a hydration sphere of about 0.4 Å which is less than the 1.1 Å typically used in hydrodynamics calculations to estimate hydration.⁶¹ When the default AER (2.84 Å) was used instead of the best-fit AER, the difference increased from 2.35 to 6.32% (Table 3). For the second calculation mode where each residue is replaced by a sphere instead of each atom and the hydrodynamic values are also calculated using a shell-model methodology, the best-fit AER was 3.98 Å with an difference of 2.50% compared to the 4.84 Å for the standard AER (7.78% difference). For the third calculation mode, which calculates the hydrodynamic values directly on the primary bead models from the second calculation mode, the best-fit AER was 5.04 Å with a difference of 2.60% compared to 6.11 Å for the standard AER (8.10% difference). Overall, the calibrated AERs were able to reproduce the experimental hydrodynamic values better than the standard default AERs. While the three modes to calculate hydrodynamic properties provide the same general information about the structure being modeled, the residue-level models were much faster in the amount of time required for calculation and could be useful for preliminary analysis of large MD simulations where thousands of structures are sampled.

Table 3. Results of HYDROPRO Global Fit Analysis.

calculation mode	AER (Å)	% difference aT	% difference s20,W	% difference Dt20,W
atom, shell model	2.19	2.35	1.19	2.24
atom, shell model	2.84	6.32	4.27	5.83
residue, shell model	3.98	2.50	1.39	2.42
residue, shell model	4.84	7.78	5.59	7.12
residue, bead model	5.04	2.60	1.41	2.50
residue, bead model	6.11	8.10	5.86	7.38

Ten thousand “snapshot” structures were sampled from each MD trajectory, and hydrodynamic properties were calculated for each structure using the calibrated AER values. The average calculated hydrodynamic values for each of the MD simulations are shown in Table 4. The hydrodynamic values calculated using MD snapshots agreed with previously calculated values using reported NMR structures with a difference of 1.85% for the atomic-level/shell-model mode, 1.89% for the residue-level/shell-model mode, and 1.88% for the residue-level/bead-model mode (Supporting Information, Table S1). In general, all three modes of calculation by HYDROPRO were able to accurately predict the hydrodynamic values of the G-quadruplex structures (Table 5). The distributions of the s_20,W values calculated using the HYDROPRO atomic-level model shell-model calculation mode (Figure 3, colored lines) are shown with the concentration-dependent c(s) experimental s_20,W distributions (Figure 3, black line). For the c(s) experimental s_20,W distributions, the width of the distribution curve is related to the homogeneity of species in solution.^62,63 Samples containing multiple species that sediment at similar rates will have broad s_20,W distributions, while highly homogeneous samples with a single predominant species (accounting for more than 90% of the total ensemble) will have narrow s_20,W distributions. In general, it was observed that sequences (143D, 2GKU, 2HY9, 2JPZ, 2JSL, and 2KF8) for which there was enough enrichment of a major species for NMR structure elucidation have narrower distributions compared to sequences for which NMR structure elucidation was not possible (1KF1 and 2KKA). The only exception was the 2JSM sequence, which was highly enriched (>70% of the total ensemble)²³ in a major species yet has a broad s_20,W distribution. Electrostatic interaction, which contributed to the nonideal behaviors of the DNA at lower salt concentrations, does not affect the width of the distributions but will shift the distribution to the left (lower apparent s_20,W). At higher concentrations of ions, the hydrodynamic behavior became more ideal, the distribution shifted to the right, and the apparent s_20,W approached the true s_20,W. Compared to the experimental distributions, the calculated s_20,W distributions were narrower and in certain cases were asymmetric. The shape of the calculated distributions is determined by the sampling capability of MD simulations which is on a much shorter time scale (1 μs) compared to the sampling capability of AUC experiments (∼6 h). The time-course graph of s_20,W values for the 2JPZ model highlights the effect of sampling time on the distribution peak shape (Figure 4F). The distribution of calculated s_20,W values across the full 1 μs of MD simulation was bimodal (Figure 3F). However, had the simulation completed within the first 500 ns, the distribution would have been narrower and unimodal.

Table 4. Summary of HYDROPRO Calculated Hydrodynamic Values.

G-quadruplex	atom/shell	residue/shell	residue/bead
143D	s20,Wa = 1.97 ± 0.02	1.94 ± 0.01	1.92 ± 0.01
	Dt20,Wa = 1.51 ± 0.01	1.49 ± 0.01	1.48 ± 0.01
1KF1	s20,W = 1.83 ± 0.02	1.89 ± 0.01	1.87 ± 0.03
	Dt20,W = 1.40 ± 0.02	1.45 ± 0.03	1.44 ± 0.03
2GKU	s20,W = 2.06 ± 0.03	2.03 ± 0.01	2.02 ± 0.01
	Dt20,W = 1.45 ± 0.02	1.44 ± 0.01	1.43 ± 0.01
2HY9	s20,W = 2.12 ± 0.04	2.15 ± 0.02	2.14 ± 0.02
	Dt20,W = 1.38 ± 0.02	1.40 ± 0.01	1.39 ± 0.01
2JSM	s20,W = 1.97 ± 0.02	1.95 ± 0.01	1.94 ± 0.01
	Dt20,W = 1.45 ± 0.02	1.44 ± 0.01	1.43 ± 0.01
2JPZ	s20,W = 2.19 ± 0.04	2.17 ± 0.02	2.17 ± 0.02
	Dt20,W = 1.43 ± 0.02	1.42 ± 0.01	1.42 ± 0.01
2JSL	s20,W = 2.09 ± 0.03	2.08 ± 0.01	2.08 ± 0.01
	Dt20,W = 1.42 ± 0.02	1.41 ± 0.01	1.41 ± 0.01
2KF8	s20,W = 1.95 ± 0.02	1.91 ± 0.01	1.89 ± 0.01
	Dt20,W = 1.49 ± 0.01	1.46 ± 0.01	1.45 ± 0.01
2KKA-Gb	s20,W = 2.02 ± 0.03	2.00 ± 0.01	1.99 ± 0.01
	Dt20,W = 1.49 ± 0.02	1.47 ± 0.01	1.47 ± 0.01
2KKA-Ib	s20,W = 2.02 ± 0.03	2.00 ± 0.01	1.99 ± 0.01
	Dt20,W = 1.49 ± 0.02	1.47 ± 0.01	1.46 ± 0.01

^aD_t20,W expressed in units of 10^–6 cm²/s and s_20,W expressed in units of 10^–13 s.

^bExperimental values for 2KKA-G and 2KKA-I were obtained with the oligonucleotide sequence dAG₃(T₂AG₃)₃T.

Table 5. Comparison of HYDROPRO-Calculated and Experimental s_20,W.

structure	% diff. atom/shell	% diff. residue/shell	% diff. residue/bead
143D	3.76	1.96	1.19
2GKU	0.30	0.83	1.23
2HY9	0.90	0.35	0.16
2JPZ	1.70	0.95	0.61
2JSL	1.15	1.46	1.68
2JSM	2.23	3.23	3.60
2KF8	1.95	3.95	4.59
1KF1	7.23	3.80	4.91
2KKA-Ga	1.88	2.67	3.11
2KKA-Ia	1.98	2.98	3.45

^aExperimental values for 2KKA-G and 2KKA-I obtained with the oligonucleotide sequence dAG₃(T₂AG₃)₃T.

Figure 4.

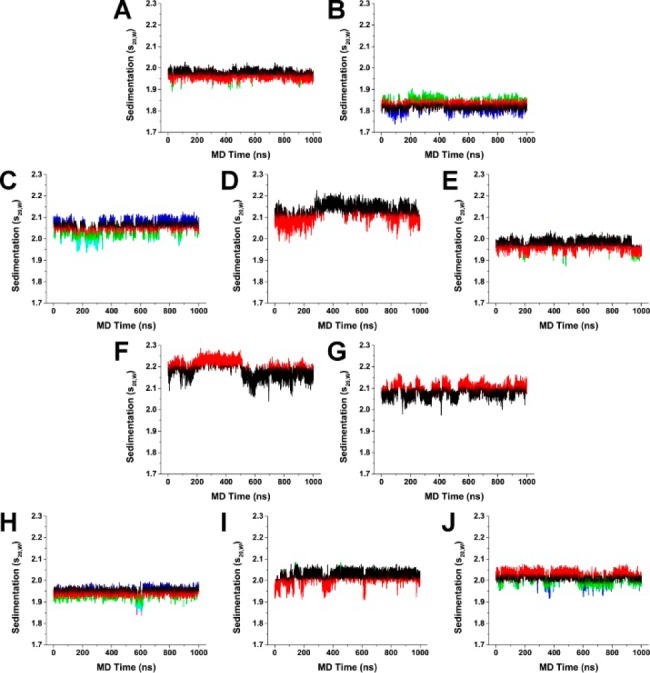
Hydrodynamics substates identified by clustering of HYDROPRO calculated sedimentation coefficients (S20,W) for 143D (A), 1KF1 (B), 2GKU (C), 2HY9 (D), 2JSM (E), 2JPZ (F), 2JSL (G), 2KF8 (H), and 2KKA (I). The most populated cluster for each model was colored black, and the second most populated cluster was colored red. Additional clusters were colored accordingly (green, blue, cyan, and magenta) in the order of decreasing population density.

With the exception of the hTel22 sequence in potassium (1KF1), the HYDROPRO calculated hydrodynamic values agreed with the experimental values (Table 5). As hydrodynamic experiments are essentially low-resolution measurements, a difference between calculated and experimental values by 5% (the precision limit for hydrodynamic measurements⁵⁹) can be considered acceptable. The % difference in Table 5 was determined by comparing the HYDROPRO calculated values from Table 4 with the experimental values in Table 2 using eq 1. For the seven models used in the HYDROPRO calibration procedure, the calculated distributions agreed with the experimental distributions (0.30–3.76% difference), as shown in Table 5. With the 143D model, it appeared initially that the model did not agree with the experimental data (Figure 3A); however, the difference of 3.76% (Table 5) was still within the experimental precision limit.

Of the three models which were excluded from the calibration procedure, the calculated distribution of 1KF1 did not agree with the experimental distribution with a difference of 7.23% (Table 5). The current findings agreed with previously reported data, which demonstrated that the parallel form of 1KF1 has different hydrodynamic behaviors compared to the ensemble of structures in solution.³⁹ The conclusion that the 1KF1 structure was distinct from the 1KF1 sequence in solution was made on the basis of the calculated s_20,W value alone and not the D_t20,W value, which appeared to agree better with the experimental value than the s_20,W. The accurate experimental determination of D_t20,W can be difficult in a solution containing multiple species as the differential migrations of different species can result in a broadening of the sedimentation boundary and an incorrect apparentD_t20,W.^62,63 For the 1KF1 structures in solution, there is a mixture of at least three to four G-quadruplex species in solution.³³ For that reason, the apparent D_t20,W value determined by experimental measurement might not be representative of the structures in solution and was reported only to complete the data even though it might not be appropriate to use it to rule in or rule out a certain structure in solution. For the other two models (2KKA-G and 2KKA-I), the calculated hydrodynamic values differed from the experimental values only slightly (1.88–1.98% difference). It should be noted that the unsubstituted 2KKA-G (1.88%) model agreed better with experimental results than the inosine-substituted 2KKA-I (1.98%) model. However, this difference is too small to draw any definitive conclusion regarding a possible difference between the two models. These findings highlighted a major limitation of HBM, which is that hydrodynamic measurements are inherently low resolution. The model that accurately predicts the hydrodynamic parameters measured in solution is not necessarily representative of the definitive structure for that molecule but rather one of the possible conformations among many others.⁴⁴ Thus, it can be concluded that the 2KKA-G and 2KKA-I models represent a possible set of conformations for the G-quadruplex structures in solution. However, this prediction should be confirmed by nonhydrodynamic experiments (e.g., 2-aminopurine fluorescence spectroscopy to probe the solvent accessibility of adenine bases or DMS footprinting to probe guanine base-pairing interactions). Such experiments were done by Li et al.³⁹ Overall, the present findings demonstrated that HYDROPRO calculations can accurately predict the correct hydrodynamic properties and can be used as a screening tool to initially rule out “incorrect” structures associated with other G-quadruplex-forming sequences.

Clustering of Molecular Dynamics Trajectories into Hydrodynamic Substates

The results of HYDROPRO calculations revealed that sedimentation rates can differ dramatically between different “snapshot” structures within the same MD trajectory (Figure 4). To identify different hydrodynamic substates within the MD trajectories, hierarchical cluster analysis was performed using HYDROPRO calculated s_20,W values as the clustering criterion. The results of the cluster analysis indicated that heterogeneous mixtures of G-quadruplex structures were present in simulations (Supporting Information, Figures S4–S13). Cluster analysis was able to identify key differences between the 2KKA-G model and the 2KKA-I model which were not apparent by s_20,W calculation alone (Figure 3I). The 2KKA G-quadruplex structures consist of a two-stack G-tetrad stem that is capped by a triple-base cap and a double-base cap on either end. In the 2KKA-I model, the G-G-I triple-base cap was slightly offset from the G-tetrad bases (Supporting Information, Figure S13), while, in the 2KKA-G model, the G-G-G triple-base cap was directly on top of the G-tetrads (Supporting Information, Figure S12). It was unclear whether the direct triple-base cap conformation is simply a new stable conformation or if it is an indication of the G-quadruplex structure transitioning to a new folding topology, as it is beyond the current capacity of MD to model such a phenomenon. The current findings clearly demonstrated that the substitution of inosine for guanine played a critical role in stabilizing the selected G-quadruplex structures. In addition, these findings raised the need for additional experimental investigation into the role of these noncanonical bases in selecting for a G-quadruplex topology from an ensemble of structures.

In addition to the HYDROPRO calculated hydrodynamic values, free energy values (ΔG) and the number of water bound were also determined for each cluster (Table 6). Free energy was calculated using the MMPBSA method and is the sum of all the molecular mechanics energies (bond, angle, torsion, van der Waals, and electrostatic) and the solvation energy (calculated using a numerical solution of the Poisson–Boltzmann equation).⁶⁴ The free energy values did not include an estimate of solute entropy, which is the least reliable component of MMPBSA calculations.⁶⁵⁻⁶⁷ The results of the cluster analysis demonstrated that G-quadruplex structures remained highly polymorphic even with the limited sampling of MD simulations. In general, it was observed that the more populated substates were more energetically favorable (i.e., lower ΔG). The G-quadruplex structures in these substates were more spherical (i.e., lower f/f₀) and compact (i.e., higher s_20,W), and were characterized by favorable interactions between the loops and flanking bases with the G-tetrad stems (Supporting Information, Figures S4–S13). For example, in the case of the 2HY9 sequence, which contained a three-residue long 5′ flanking sequence and a two-residue long 3′ flanking sequence, the more compact structures featured stacking interactions between the flanking bases and the G-tetrads, while the less compact structures did not. Previous studies have reported that the folding of a single-stranded DNA structure into the G-quadruplex form was associated with the release of water molecules from the DNA into the surrounding environment.^68,69 It was observed that the more compact structures were also associated with a reduced number of bound water molecules. As hydration plays an important role in ligand binding and recognition,⁷⁰⁻⁷³ for instance, the binding of groove-binding small molecules to duplex DNA is driven by water being displaced from the minor grooves.⁷⁴ Therefore, clustering by s_20,W values can be used in the process of drug design to identify substates that could interact more favorably with small-molecule inhibitors.

Table 6. Results of s_20,W Cluster Analysis on MD Trajectories.

structure	cluster no.	N	s20,Wa	f/f0	ΔGa	no. of water
143D	1	6170	1.98	1.12	–4421.89	165.26
	2	3802	1.95	1.14	–4421.62	166.92
	3	28	1.91	1.16	–4416.97	169.89
1KF1	1	5244	1.82	1.22	–4360.05	174.63
	2	3503	1.84	1.20	–4363.84	173.62
	3	768	1.87	1.19	–4368.20	173.43
	4	485	1.78	1.24	–4357.99	176.97
2GKU	1	4694	2.07	1.14	–4664.48	174.66
	2	2482	2.04	1.15	–4664.43	176.61
	3	1413	2.01	1.17	–4664.29	178.65
	4	1167	2.09	1.13	–4663.50	172.86
	5	244	1.98	1.19	–4664.01	181.28
2HY9	1	6374	2.15	1.16	–5094.00	190.93
	2	3626	2.08	1.19	–5091.86	197.55
2JSM	1	6852	1.98	1.15	–4536.80	175.92
	2	3115	1.95	1.17	–4533.68	177.01
	3	32	1.90	1.19	–4525.48	178.38
	4	1	2.04	1.13	–4545.97	172.00
2JPZ	1	6009	2.16	1.14	–4933.18	188.59
	2	3991	2.23	1.12	–4930.52	180.50
2JSL	1	6681	2.07	1.16	–4811.53	186.55
	2	3319	2.12	1.14	–4817.04	184.74
2KF8	1	5471	1.96	1.14	–4241.88	166.86
	2	3892	1.93	1.15	–4239.20	168.79
	3	411	1.90	1.16	–4224.43	170.41
	4	186	1.98	1.13	–4247.06	164.19
	5	36	1.87	1.18	–4215.53	172.75
	6	4	1.84	1.20	–4205.31	171.50
2KKA-G	1	7863	2.03	1.13	–4434.13	171.78
	2	2135	1.98	1.15	–4427.76	175.58
	3	2	2.09	1.11	–4409.13	179.00
2KKA-I	1	4673	2.01	1.14	–4347.30	172.24
	2	4146	2.04	1.12	–4347.99	170.08
	3	1068	1.98	1.15	–4343.95	173.96
	4	111	1.94	1.17	–4340.41	176.68
	5	2	2.08	1.11	–4331.61	162.00

^as_20,W is expressed in units of 10^–13 s; ΔG is expressed in units of kcal/mol.

Principal Component Analysis of Molecular Dynamics Trajectories

PCA was employed to identify the major patterns of motions in the MD models and investigate the underlying mechanism for the formation of the different substates identified by clustering analysis. Motions from MD can appear random and chaotic; however, most of the fluctuations associated with the MD models can usually be reduced to several low-frequency eigenvectors with large eigenvalues.⁷⁵ The first, second, and third eigenvectors are depicted using “porcupine” plots^76,77 with the arrows representing the magnitude and direction for the eigenvector for each atom (Figure 5 and Supporting Information, Figures S14 and S15). In general, it was observed that the overall dynamics of the G-quadruplex structures were composed of only one to five major movements, as indicated by the large eigenvalues associated with the first several eigenvectors compared to subsequent eigenvectors (Supporting Information, Figure S16). In fact, the first three eigenvectors accounted for 30–80% of the variance in the models (Supporting Information, Figure S17). The porcupine plots indicated that motions related to the more rigid green colored stems (Figure 5 and Supporting Information, Figures S14–S15) tend to be small and localized, while the motions related to the more flexible red loops (Figure 5 and Supporting Information, Figures S14 and S15) and blue flanking bases (Figure 5 and Supporting Information, Figures S14 and S15) were more prominent. Each structural component was defined by characteristic movements. Most of the movements associated with the stem structures were the twisting motions of the phosphate backbone around the quadruple helix stack. The major movements associated with the loop structures were rotation of the phosphate backbone which moved the bases either toward the G-tetrad stem or away from it. In agreement with previous atomic positional fluctuation results, higher magnitude movement was seen with the chain-reversal loops compared to the lateral and diagonal loops. Lastly, the transition between flanking bases stacking on the G-tetrad bases to the unstacking of the flanking bases was observed as the major movement associated with the flanking bases. The movements associated with structures containing longer flanking sequences (i.e., 2HY9 and 2JPZ) were much higher in magnitude. The movements identified by PCA correlated with the structural differences between the different substates previously identified by cluster analysis.

Figure 5.

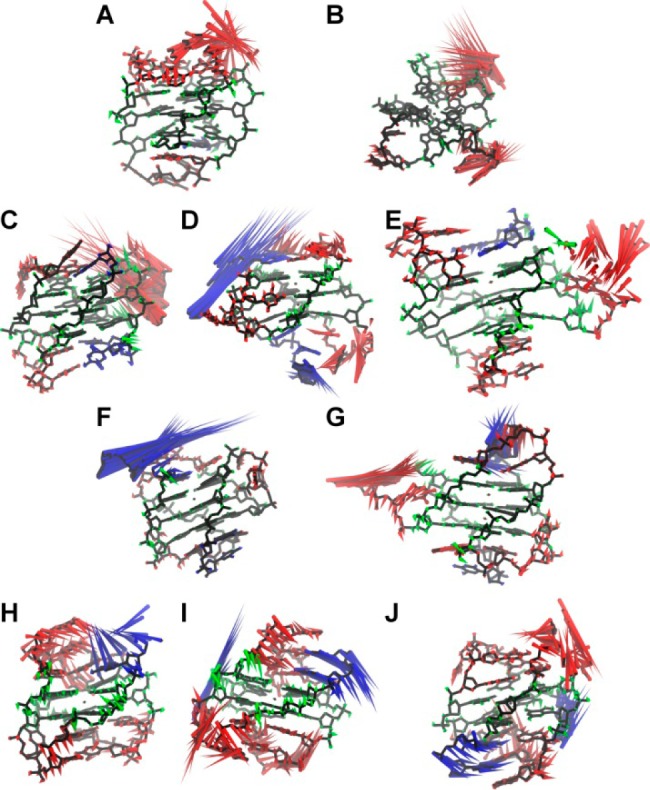
Porcupine plots of the first eigenvectors for 143D (A), 1KF1 (B), 2GKU (C), 2HY9 (D), 2JSM (E), 2JPZ (F), 2JSL (G), 2KF8 (H), 2KKA-G (I), and 2KKA-I (J). Principal component analysis was carried out on MD trajectories in order to determine the major patterns of motions. Motions associated with stem residues are colored green, loop residues are red, flanking residues are blue, and central ions are yellow.

The first 10 eigenvalues are reported (Supporting Information, Figure S16) as calculated for the G-quadruplex structures as a whole and for various structural components (i.e., stem, loops, flanking bases). The eigenvalues were slightly reduced when the more mobile hydrogen atoms were removed from the analysis. Because PCA is sensitive to the scaling of the original data, the eigenvectors and eigenvalues of similar motions should be similar to one another. An overlap of the eigenvalues of loop and flanking bases with the eigenvalues of the overall G-quadruplex structures indicated that overall dynamic motions of G-quadruplex structures are mainly due to motions of loop and flanking bases. To demonstrate this correlation between the dynamics motions of individual structural components and the overall dynamic motions of the G-quadruplex structures, the first principal components were plotted as a function of the second principal components for all 10 MD models for overall G-quadruplex structure and the individual stem, loop, and flanking structures (Supporting Information, Figures S18–S27). From the PCA results, each model can be classified as having loop-dominated dynamics (i.e., 143D, 1KF1, 2GKU, 2JSM), flanking bases-dominated dynamics (i.e., 2HY9 and 2JPZ), and mixed dynamics with contributions from both loop and flanking bases (i.e., 2JSL, 2KF8, 2KKA-G, and 2KKA-I). Overall, the PCA findings help explain the differences in hydrodynamic values for individual substates identified by previous cluster analysis. In addition, the differences observed between the dynamic motions of different loop and flanking bases could have significant implications in drug interaction and the choices of sequence chosen for in vitro drug binding studies.

Investigation of Water and Cation Distribution around G-Quadruplex Structures

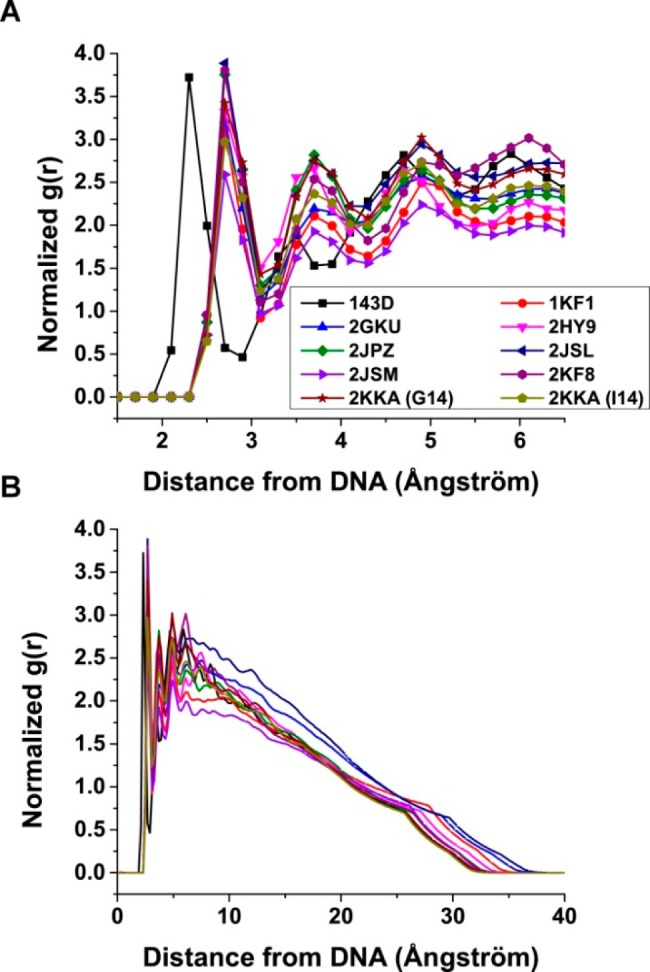
Given the importance of hydration and cations in influencing G-quadruplex formation, as well as the role of water and ions in determining hydrodynamic properties of a macromolecule, density mapping and radial distribution functions (RDFs) were used to visualize the distribution of these molecules around the G-quadruplex structures and provide a general overview of hydration and cation binding. The RDFs of the distance between oxygen atoms of the water molecules and non-hydrogen atoms on the surface of the G-quadruplex structures indicated the formation of a well-defined first hydration shell between 2.4 and 3.2 Å around the G-quadruplex structures (Figure 6). The second and third hydration shells can also be observed, although these peaks were not as sharp as the peaks for the first hydration shell. To visualize these hydration shells, density mapping of the water molecules over the duration of the trajectory was performed. Water density is shown contoured at equivalent levels (about 2 times the expected bulk water density) around the average structures from the MD trajectories (Supporting Information, Figure S28). The condensation of the water around the G-quadruplex structure was evident. While the water appeared to be evenly distributed around the G-quadruplex structures, a higher density of water was observed around the rigid stem structures and a lower density was observed around the more mobile loops and flanking structures. This observation agreed with a previous study, which reported that rigid structures are associated with more well-defined water positions and higher apparent density.⁷⁸ When contoured at a higher level (about 3 times the expected bulk water density), preferential binding of water to the grooves of the G-quadruplex structures became more apparent. At this higher contour level, a “spine of hydration” which traverses the grooves of the G-quadruplex structures was observed (Figure 7). These findings demonstrated the interaction of water molecules with DNA and suggested a role for hydration in maintaining the G-quadruplex structures.

Figure 6.

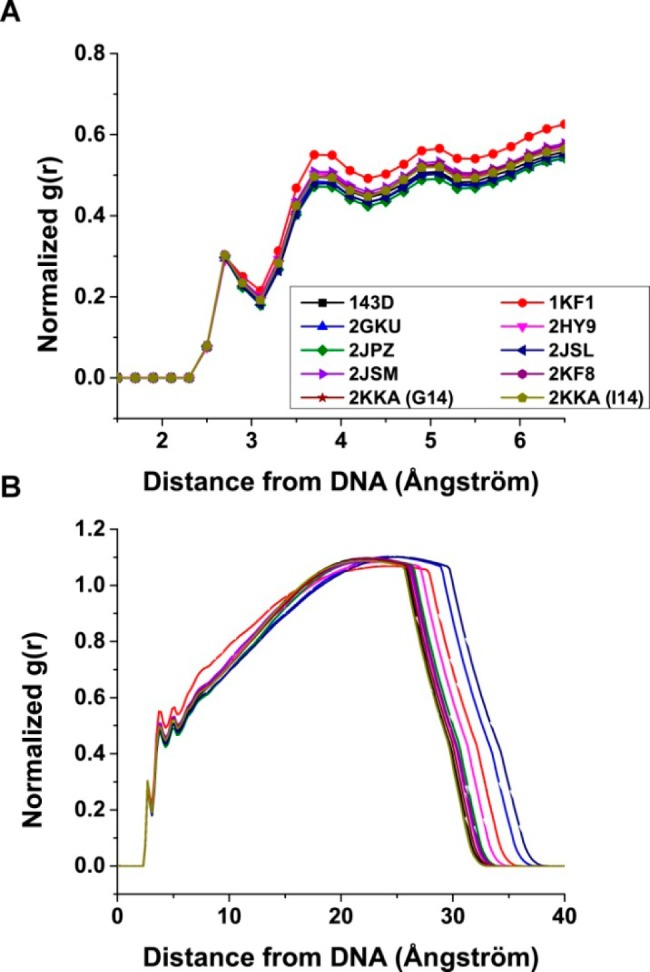
Radial distribution functions (RDFs) between G-quadruplex surface heavy atoms (no hydrogen) and water oxygen atoms. RDFs were calculated for distances from 1.5 to 6.5 Å (A) and for distances from the G-quadruplex surface to the edge of the periodic box.

Figure 7.

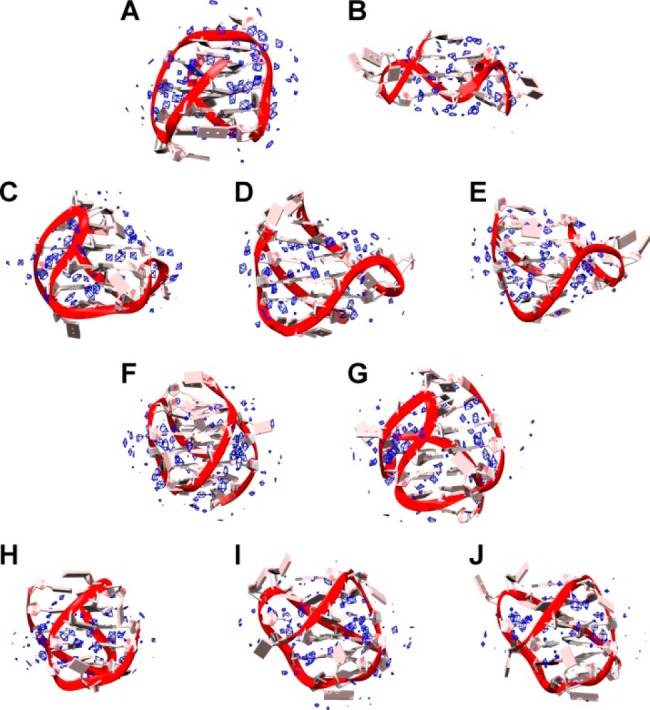
Pseudodensity grid maps of water oxygen atoms for 143D (A), 1KF1 (B), 2GKU (C), 2HY9 (D), 2JSM (E), 2JPZ (F), 2JSL (G), 2KF8 (H), 2KKA-G (I), and 2KKA-I (J). Water density (blue) was contoured at 3× the density (55.5 M) of bulk water. The average structure of each G-quadruplex over the trajectory is shown.

The RDF plots of the distance between cations and G-quadruplex structures indicated cations interacted with G-quadruplex structures differently from water (Figure 8). The RDF plots showed a clear attraction of positively charged cations to the negatively charged nucleic acids with a high density of cations closer to the DNA and decreased density further out. The interaction shells for the sodium ions were closer to the DNA than those for the potassium ions. This observation was expected given that within the force field the sodium ions are smaller (radius = 1.369 Å vs 1.705 Å)⁷⁹ and thus can be closer to the G-quadruplex structures. Four cation interaction shells were observed for each structure. The first two interaction shells were well-defined, while the second two interaction shells were more diffused. Density mapping analyses were performed to visualize these cation shells. The density was contoured at the reference density (Supporting Information, Figure S29). At this contour level, two different modes of interaction were observed. The first mode was the coordination of cations within the central G-tetrads. It was observed that the cations remained positioned between the stacked G-tetrads throughout the simulation with no exchange between the G-quadruplex stem and the bulk solvent as observed in other simulations.⁸⁰⁻⁸² The 143D model of the hTel22 sequence in sodium containing solution is noteworthy, as the starting structure contained three sodium ions placed within the plane of the G-tetrads. However, when the system was equilibrated, one of the sodium ions were ejected from the G-quadruplex stem into the surrounding solvent and the remaining two sodiums assumed positions between the G-tetrads and remained so for the course of the MD trajectory. In addition to the central coordination, diffused interaction of the cations along the grooves of the G-quadruplex structures was also observed. These “spines of cations” were not deep within the grooves as were the “spines of hydration”. Instead, they were closer to the backbones and interacted with the backbone phosphate groups. When the cations were contoured at a higher level, these electrostatic interactions began to disappear and a third mode of interaction, external coordination with loops and flanking bases, was observed (Figure 9). These externally coordinated cations were critical in maintaining loop and flanking base positions. For instance, potassium binding was responsible for stabilizing the capping structures in the 2KF8 model. The binding site at the top of the G-quadruplex structure remained 100% occupied with the potassium ion either coordinated within the plane of the triple-base cap or stacked between the planes of the inner triple-base cap and the outer double-base cap. Cation stabilization of loop structures has also been observed in previous simulations³⁷ as well as experimentally in the crystal structure of the human c-Kit DNA promoter sequence.⁸³ In that study, one Mg²⁺ and two K⁺ ions were observed in the G-quadruplex loops and grooves in addition to the K⁺ ions within the canonical central ion channel. In the crystal structure, all three external cations are believed to play a role in maintaining the c-Kit G-quadruplex structure. It should be noted that one of the K⁺ ions appeared to be transient and capable of adopting one of several distinct positions, while the other K⁺ ion appeared to be more static, suggesting the existence of a high affinity binding site. While the K⁺ ions are believed to have a primary role in stabilizing the G-quadruplex structure by direct electrostatic interaction with the DNA, the Mg²⁺ ion is thought to assume a secondary role of shielding the anionic charge of the phosphate groups. In fact, it is well-known that polyanions, like DNA, can attract a shell of cations to help partially neutralize the negatively charged backbone phosphates.^84,85 Together, these findings suggest that, in addition to stabilizing the G-tetrads within the G-quadruplex core, cations can also play other roles in promoting G-quadruplex formation and stability.

Figure 8.

Radial distribution functions (RDFs) between G-quadruplex surface heavy atoms (no hydrogen) and cations. RDFs were calculated for distances from 1.5 to 6.5 Å (A) and for distances from the G-quadruplex surface to the edge of the periodic box.

Figure 9.

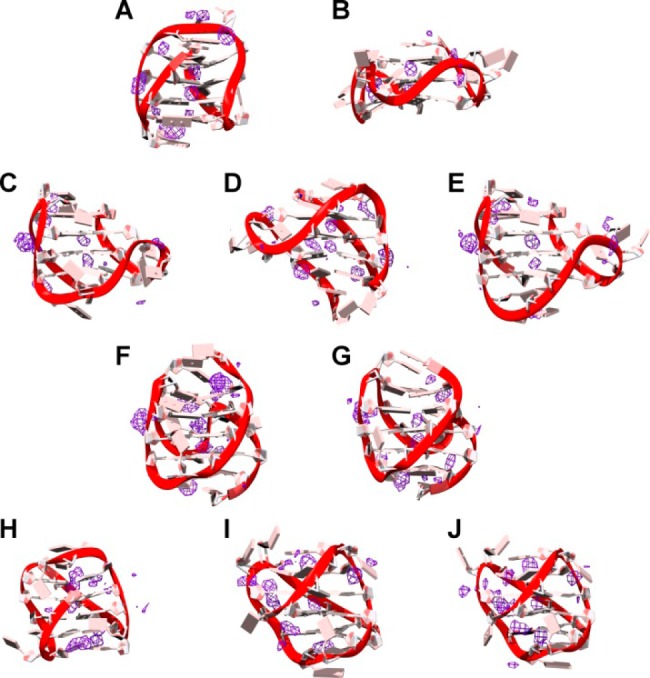
Pseudodensity grid maps of cations for 143D (A), 1KF1 (B), 2GKU (C), 2HY9 (D), 2JSM (E), 2JPZ (F), 2JSL (G), 2KF8 (H), 2KKA-G (I), and 2KKA-I (J). Cation density (purple) was contoured at 3× the density of sodium (6 M) for 143D and at 3× the density of potassium (4 M) for the other G-quadruplex structures. The average structure of each G-quadruplex over the trajectory is shown.

Effects of Cation Binding on Hydrodynamic Calculations

HBM was used to provide information about the number of cations bound to the G-quadruplex structures. This use of HBM is based on the premise that the hydrodynamic properties are dictated by the size (volume and mass) and shape of a macromolecule in solution. When accurate experimental information is known about the volume and shape of the G-quadruplex structure, HBM can be used to estimate the mass of the G-quadruplex and, by extension, the number of cations bound to it. To illustrate this, a series of HYDROPRO calculations were performed. The additions of potassium or sodium to the G-quadruplex structure were accounted for by changing the molecular weight value in the HYDROPRO parameter file. For example, for a G-quadruplex structure with no potassium bound the molecular weight value used was the molecular weight of the DNA only. Whereas, for a G-quadruplex structure with two potassium ions bound, the molecular weight value used was the sum of the molecular weight of the DNA and two times the molecular weight of potassium. The calculations were done using all three modes of HYDROPRO calculation with the default AER instead of the calibrated AER. In order to display the data for the sequences on the same scale, the number of ions bound was normalized using eq 5:

5

The results of the HYDROPRO calculations are shown in Figure 10. For the atomic-level hydrodynamic bead models, the lowest errors were observed at about 50% charge neutralization (i.e., about 10–13 cations), while, for the coarser residue-level models, the lowest errors were observed at about 60% charge saturation (i.e., about 12–15 cations). The findings agreed well with previous studies which reported 10–11 potassium ions bound to the hTel22 sequence in 30 mM KCl buffer.⁸⁶ This demonstrates that HBM may have application beyond structural prediction.

Figure 10.

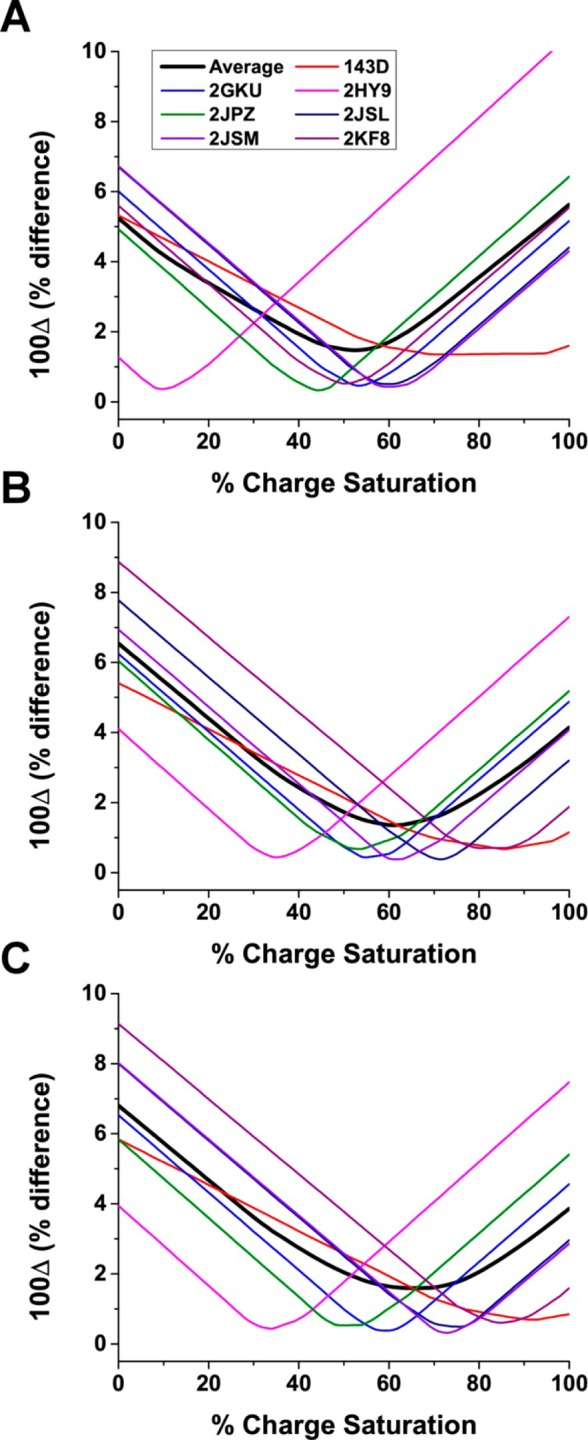
s_20,W values as a function of the number of bound cations. The values for 100Δ as a function of percent charge saturation for the primary hydrodynamic model calculated using the seven G-quadruplex structures formed from the human telomere sequence. Hydrodynamic properties of G-quadruplexes were calculated using atomic-level shell-model calculation (A), residue-level shell-model calculation (B), and residue-level bead-model calculation (C).

Conclusion

HBM was demonstrated to be a powerful tool for studying G-quadruplex structures when atomic-level structural representations are unavailable, ambiguous, or cannot be determined experimentally. In such cases, the use of low-resolution techniques such as hydrodynamics, combined with readily accessible biophysical measurements (e.g., CD spectroscopy, fluorescent spectroscopy), can be used to obtain general information regarding the G-quadruplex structure, size, and shape. HBM can bridge low-resolution hydrodynamic measurements and high-resolution molecular modeling to provide further information regarding these structures. For example, HBM can be used to estimate the number of cations bound to the G-quadruplex structure. When applied to the study of novel G-quadruplex-forming sequences, HBM can be used to rule out structures that are not representative of the ensemble as was the case with 1KF1 whose calculated values differed greatly from the experimental values. However, hydrodynamics remains a low-resolution technique and molecular models for which calculated hydrodynamic values agreed (or differed only slightly) with experimental values will need to be confirmed with additional hydrodynamic and biophysical measurements, as was the case with the 2KKA-G and 2KKA-I models.

Another limitation of hydrodynamics and HBM is that the calculation is typically performed on one structure giving a static look at an otherwise dynamic system. HYDROPRO can only calculate hydrodynamic values for a single structure at any given time. However, as demonstrated, HBM can be used in tandem with MD simulations to provide a more dynamic representation of the macromolecule. In addition, the high-resolution nature of molecular dynamics can help complement the low-resolution nature of hydrodynamic measurements. As was observed with the 2KKA-G and 2KKA-I models, hydrodynamics was not able to distinguish between the two sequences, as both gave rise to identical sedimentation and diffusion values. However, cluster analysis of the MD trajectories revealed that the 2KKA-G model was more heterogeneous than the 2KKA-I model and demonstrated the effect of inosine substitution on selecting for a particular G-quadruplex topology. The findings demonstrated that molecular dynamics can supplement HBM in the study of G-quadruplex structures.

For G-quadruplexes, it is recommended to use either the atomic-level model with the shell-model calculation mode (AER = 2.19 Å) or the residue-level model with the bead-model calculation mode (AER = 5.04 Å) for HYDROPRO calculations, as both modes can predict the hydrodynamic properties accurately with a reasonable estimate of the size of the macromolecule. The atomic-level model with shell-model calculation is considered the gold standard and should be used whenever the most rigorous calculation is required. The residue-level model with the bead-model calculation mode has the advantage of being significantly faster (by several orders of magnitude) but with a slightly higher error in predicting hydrodynamic properties. For molecular weight, the recommended value is the molecular weight of the DNA and internal coordinating cations. For Na⁺, because these ions are smaller and can fit within the G-quartet plane, the number of internal coordinating ions is equal to the number of G-quartets. For K⁺, which is bigger and thus can only fit in between the planes of the G-quartets, the number of internal coordinating ions is one less than the number of G-quartets. The parameters for HYDROPRO presented can be used for hydrodynamic calculation of G-quadruplexes or can be further optimized by fitting with additional hydrodynamic values (i.e., rotational diffusion coefficients, NMR relaxation time, intrinsic viscosity, etc.). Although this work was conducted on the human telomere sequence, the experimental approach outlined can be easily adapted for other G-quadruplex-forming sequences to propose relevant G-quadruplex structures that can be used as a basis for drug design.

Glossary

Abbreviations

AUC

analytical ultracentrifugation

CD

circular dichroism

EDTA

ethylenediaminetetraacetic acid

MD

molecular dynamics

MMPBSA

molecular mechanic Poisson–Boltzmann surface area

NMR

nuclear magnetic resonance

RDFs

radial distribution functions

RMSD

root-mean-square deviation

SV

sedimentation velocity

Supporting Information Available

Figures showing the following: (Figures S1 and S2) atomic fluctuation calculations per atom and per residue over the MD trajectories, (Figure S3) a_T calibration plot for HYDROPRO, (Figures S4–S13) representative structures from cluster analysis, (Figures S14 and S15) porcupine plots of second and third eigenvectors for MD trajectories, (Figure S16) plots of the first 10 eigenvalues for each MD trajectory, (Figure S17) plots of percent of variance explained by the first 10 eigenvectors, (Figures S18–S27) plots of the first eigenvectors vs the second eigenvectors for each G-quadruplex structure, stems, loop, and flanking bases, (Figure S28) pseudodensity grid maps of water at 2× bulk water density, and (Figure S29) pseudodensity grid maps of cations at reference density. Also, Table S1 compares hydrodynamic values computed from MD simulations versus NMR structures. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States