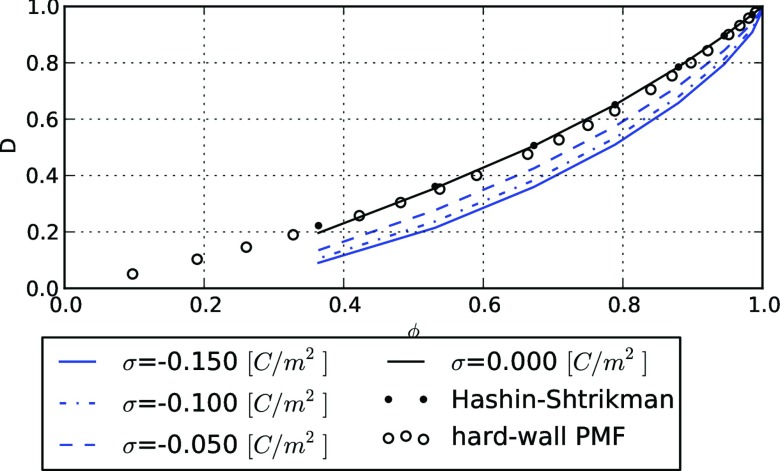
Figure 2.

Predicted normalized effective diffusion constants (D) as a function of accessible volume fraction (ϕ), where D = 1.0 signifies equivalence with an arbitrary bulk diffusion constant. For a box-shaped, repulsive potential of mean force (PMF) representing a cylindrical obstacle (open circles), the quantitative agreement with the analytical Hashin-Shtrikman (HS) upper bound (dots) indicates that the homogenized Smoluchowski equation (HSE) with a hard-wall PMF sufficiently describes the influence of obstacles. Diffusion constants for a negatively charged diffuser (z = −1) with neutral (σ = 0, black) and electro-negative explicit cylinders (σ < 0, blue) shows that the HSE using an electrostatic potential quantitatively agrees with results from Ref. 27 which showed that repulsive interactions slow diffusion.