Abstract
The balance response direction to electrically evoked vestibular perturbation is closely tied to head orientation. Such craniocentric response organization is expected of a simple error correction process. Here we ask whether this is maintained when the body is made more stable, but with the stability being greater in one direction than another. Since it is known that vestibularly evoked balance responses become smaller as body stability increases, the following two outcomes are possible: (1) response magnitude is attenuated, but with craniocentricity maintained; and (2) anisotropy of stability is considered such that components of the response are differentially attenuated, which would violate a craniocentric organizing principle. We tested these alternatives by measuring the direction of balance responses to electrical vestibular stimulation across a range of head orientations and stance widths in healthy humans. With feet together, the response was highly craniocentric. However, when stance width was increased so that the body was more stable in the frontal plane, response direction became biased toward the sagittal direction. This resulted in a nonlinear relationship between head orientation and response direction. While stance width changes the mechanical state of the body, the effect was also present when lateral light touch was used to produce anisotropy in stability, demonstrating that a significantly altered mechanical state was not crucial. We conclude that the balance system does not simply act according to the direction of vestibular input. Instead, it appears to assign greater relevance to components of vestibular input acting in the plane of lesser body stability than the plane of greater body stability, and acts accordingly.
Introduction
Processing of vestibular input can be readily studied by passing a current between mastoid electrodes [galvanic vestibular stimulation (GVS)]. GVS evokes a net vestibular signal that is equivalent to a head rotation approximately around the roll axis of the head (Day and Fitzpatrick, 2005). The brain responds as though the apparent head rotation were produced by an unplanned body movement. In a standing subject, the magnitude of the whole-body response varies with the state of stability of the body, suggesting that the response emanates from the balance system (Day et al., 1997). In general, the more stable the body, the smaller the response to a given input (Britton et al., 1993; Fitzpatrick et al., 1994; Day et al., 1997; Horak and Hlavacka, 2001; Welgampola and Colebatch, 2001). This demonstrates that the balance response to vestibular input is not organized to simply correct the vestibular error signal, but rather suggests a degree of state or context dependence.
Another well established phenomenon is the craniocentric nature of vestibularly evoked balance responses. When facing forward, the GVS-evoked signal is interpreted as the body falling to the side, to which the balance system responds by driving the body toward the opposite side. When the head is turned, the direction of the motor response turns by a similar amount (Lund and Broberg, 1983; Hlavacka and Njiokiktjien, 1985; Pastor et al., 1993; Mian and Day, 2009a). This apparent craniocentric principle of response organization seems appropriate because the direction of the vestibular signal, being fixed in the skull, is itself craniocentric.
An interesting challenge to this craniocentric principle comes when one considers its potential interactions with the state dependence of the balance response. For example, if the head were turned to the side through 45°, one would ordinarily expect the response direction to be similarly turned through 45°, as has been observed previously (Pastor et al., 1993; Mian and Day, 2009a). Thus, the response would have equal components in the sagittal and frontal planes. What would happen if the body were made more stable in one direction than another? This can be achieved, for example, by increasing stance width, which stabilizes the body overall but more in the frontal than the sagittal plane (Day et al., 1993). Certainly, according to the known state-dependent property, there will be a reduction in the magnitude of the response. But beyond that, two possibilities can be conceived. One is that the state dependence of the response is isotropic, with equal attenuation of both components. In this case, response direction, and thus craniocentricity would be maintained. This possibility is not ruled out by prior studies of state dependence of the response, which have been limited to a single plane of action. The other possibility is that the component in the more stable plane would be attenuated to a greater extent than the component in the less stable plane. Anisotropic attenuation would produce a response direction no longer at 45° and so would violate the principle of craniocentricity. Here we investigate these two possible outcomes.
Materials and Methods
Participants
Male and female adult humans aged 18–39 years with no known history of neurological or vestibular dysfunction took part in these experiments (for group characteristics for each experiment, see Table 1). The study was approved by the University College London Research Ethics Committee and conformed to the Declaration of Helsinki. All participants gave written informed consent. A subset of data from experiment 2b was previously reported in a meeting abstract (Mian and Day, 2009b).
Table 1.
Participant characteristics
| Experiment |
|||||
|---|---|---|---|---|---|
| 1 | 2a | 2b (0 cm stance width)a | 2b (6 cm stance width)a | 3 | |
| Participants | |||||
| Total (N) | 15 | 7 | 11 | 6 | 11 |
| Male (n) | 2 | 2 | 4 | 1 | 6 |
| Female (n) | 13 | 5 | 7 | 5 | 5 |
| Age (years) | 23 ± 3 | 26 ± 7 | 26 ± 6 | 30 ± 5 | 29 ± 7 |
| Height (cm) | 166 ± 7 | 167 ± 13 | 171 ± 11 | 171 ± 12 | 173 ± 8 |
| Mass (kg) | 61 ± 10 | 68 ± 11 | 64 ± 11 | 69 ± 11 | 70 ± 11 |
Data are reported as the mean ± SD, unless otherwise indicated.
aFor experiment 2b, separate samples were used for 0 and 6 cm stance width conditions.
Experimental plan
Three experiments were undertaken to study the interaction between craniocentricity and state dependence of the balance response evoked by electrical vestibular stimulation. In experiments 1 and 2, the interaction was studied by measuring the balance response at varying stance widths, initially with the head turned 45° in yaw (experiment 1) and then over a wider range of head angles (experiment 2). In experiment 3, we then examined the interaction using light touch, instead of stance width, to attain anisotropy in body stability (Rabin et al., 1999) without significant change in the mechanical state of the body.
We initially (experiment 1) used direct current waveforms (GVS) as the form of stimulation. However, in experiments 2 and 3, quasi-random currents were delivered [stochastic vestibular stimulation (SVS)]. The time–domain correlation between SVS and motor output is similar to the averaged evoked response to GVS (Dakin et al., 2007). We opted to switch to using SVS in experiment 2 as data collection can be achieved more quickly and with greater signal-to-noise ratio than with GVS. This was desirable given the high number of conditions in experiment 2b.
General procedures
Carbon rubber electrodes coated with conductive gel were attached to skin overlying the mastoid processes using adhesive tape and a headband. Binaural bipolar stimuli (anode on one side, cathode on the other) were delivered from a computer-controlled current source. With this electrode configuration, one would expect a balance response in the direction of the anode (Fitzpatrick and Day, 2004). Ground forces (9286AA, Kistler) and stimulus waveform were recorded at 1000 Hz, and the position of markers attached to the head and the spine at C7 were tracked at 50 Hz using a motion capture system (CODA Cx1, Charnwood Dynamics). The forces used in the analyses are reaction forces (the forces acting on the body). Experiments were performed standing. Feet were parallel and pointing forward, and stance width refers to the distance between the medial borders of the feet. Desired head-on-feet yaw angles were achieved by having participants turn their head so their nose was pointing at strategically placed eye-height targets (eccentric gaze was not allowed). Rotation of both the neck and trunk was allowed. Before each trial, participants adopted a requested posture and then closed their eyes before data collection commenced. They opened their eyes at the end of each trial and adopted a neutral head position. Shoes were not worn. Figure 1A depicts the coordinate system in which head yaw (i.e., orientation of the interaural line in the horizontal plane) and response directions (described below) were measured.
Figure 1.
Methods. A, The coordinate system used for reporting values of θH and θR. B, Expected relationships between head yaw and response direction if response direction is strictly dependent on head yaw (dashed line) or if there is directional specificity of the vestibularly evoked balance response as represented by Equation 1 in Materials and Methods (solid lines). The annotations on the plot refer to Sx/Sy ratios (see Eq. 1) for each line. C, A single-subject example of SVS–force cross-covariance, with the second peak specified by the vertical dotted line. Horizontal dotted lines denote 95% confidence intervals (Halliday et al., 1995). D, A single-subject example of measurement of the onset of body motion in experiment 1, under the 0 cm stance width condition. The solid line is the speed of the C7 marker in the horizontal plane averaged across trials, with time relative to stimulus onset. The horizontal dotted line is the threshold calculated as described in experiment 1 in Materials and Methods. The vertical dotted line marks where C7 speed crossed the threshold level. Lab, Laboratory coordinate system.
Experiment 1
Experiment 1 (N = 15) assessed the effect of stance width (0, 3, 6, and 9 cm) on GVS-evoked balance responses at a single head-on-feet yaw angle of −45°. The GVS stimulus had a 2 s duration and 1.5 mA amplitude. The experiment involved two stimulus conditions [anode right/cathode left (ARCL) and anode left/cathode right (ALCR)], giving eight conditions in total (four stance width × two polarities). Ten trials were conducted per condition, resulting in 80 trials in total. The experiment involved eight blocks of 10 trials. Quasi-randomly, stance widths were varied block by block, and stimulus polarity was varied within each block. Stimuli were presented 4.5–7 s after eye closure, and the trial ended 2 s after stimulus offset. Breaks between trials were ∼10 s, and seated rest was available between blocks.
Head angle was measured as the average head angle in the 1 s period before stimulus onset and was averaged across trials. To measure the GVS-evoked responses, the ground reaction force and C7 position data were aligned to stimulus onset and averaged across trials. Any DC bias in the force and position signals was removed by subtracting a baseline period (the 1.5 s before stimulus onset) from the time series. The afferent and motor responses to ALCR currents have been well established to be opposite of those to ARCL currents (Fitzpatrick and Day, 2004). Therefore, we collapsed data across polarities by inverting the ALCR data and combining with the ARCL data. The direction and magnitude of vectors calculated from the X and Y components of the polarity-collapsed time series were used to summarize and compare the response at times of interest. Reporting of the responses will emphasize measurements made at 0.4 s (force) and 2.0 s (C7) from stimulus onset. But it was also of interest to determine how early statistically significant differences in response directions could be determined. To this end, we measured force response directions every 5 ms (see Statistical analysis).
We were also interested in the timing of the onset of body movement. To establish when significant motion of the body first occurred (regardless of direction), we calculated the speed of the C7 marker in the horizontal plane, . We then determined the time at which the condition-averaged, polarity-collapsed speed first exceeded a baseline threshold level for at least the subsequent 250 ms. This was done separately for each subject. The threshold level was set at the SD of C7 speed measured during the 1.5 s before stimulus onset. This SD was measured separately for each trial and then condition averaged for each subject. A single-subject example of the onset of stimulus-dependent body motion measured in this way for the 0 cm stance width condition is given in Figure 1D.
Experiment 2
The potential biasing effect of anisotropic stability on response direction described in the Introduction can be represented by the following equation:
where θR is response direction, θH is head yaw angle, and c is a constant that depends on the direction of the vestibular signal in head coordinates and convention for describing θH and θR. For ARCL binaural–bipolar GVS, and the conventions used in this article, c is expected to be 0. Sx and Sy are parameters reflecting some relevant aspect of body state in the frontal and sagittal planes (e.g., the degree of instability). When Sx and Sy are unequal, a nonlinear relationship between head yaw and response direction would occur, as depicted in Figure 1B. The alternative model is that the state dependence is non-directionally specific. In this case, while the gain of the response would be dependent on some isotropic aspect of state, the response direction would remain strictly linked to head angle (Fig. 1B, dotted line).
The purpose of experiment 2 was to study the effect of stance width on vestibularly evoked balance response directions over a wide range of head yaw angles with a view to assessing the suitability of Equation 1. As noted earlier (in Experimental plan), we used SVS, rather than GVS, for this experiment. SVS is coherent with motor output over the 0–20 Hz range (Dakin et al., 2007). The SVS stimulus used in the current study had a bandwidth of 1–20 Hz [created by digitally low-pass (20 Hz) and then high-pass (1 Hz) filtering random number time series using sixth-order Butterworth filters], a peak amplitude of ±2 mA, and rms of 0.6 mA. As a preliminary step, experiment 2a (N = 7) assessed the effect of stance width (0, 3, 6, and 9 cm) on SVS-evoked balance responses at a single head-on-feet yaw angle of −45°. This was to establish initially whether the effect of stance width observed in experiment 1 was apparent when using SVS. Experiment 2b assessed SVS-evoked balance responses at 0 cm (N = 11) and 6 cm (N = 6) stance widths over a range of head-on-feet yaw angles (0°, ±15°, ±60°, and ±90°). The 0 and 6 cm conditions in experiment 2b comprised data from independent groups of participants. Data from six trials, each of 30 s duration, were collected per posture in a quasi-random order. Approximately 30 s of rest was provided between each trial, with 3 min of seated rest between blocks of trials. In experiment 2a, each block consisted of three trials, and stance width varied block to block in a quasi-random order. In experiment 2b, each block consisted of seven trials with one trial at each head angle performed within each block in a quasi-random order.
Head angle was measured as the mean head angle within each trial and averaged across trials. Data analysis to assess the direction and magnitude of SVS-evoked responses was identical to that in a previous study where it was described in detail (Mian and Day, 2009a). In brief, for each participant and posture, data were concatenated across trials, and the cumulant density function (Halliday et al., 1995; equivalent to, and hereinafter referred to as “cross-covariance”) between concatenated SVS and shear force time series was calculated using the component of the force acting in each of 360 equally spaced horizontal force axes. The axis direction that produced the largest positive value for the second peak in the cross-covariance (Fig. 1C) was taken to represent response direction, and the value of this peak was taken to represent response magnitude. The polarity convention (positive current = anode right) means that (as an aid to interpretation) the direction of this axis can be thought of as the response direction to ARCL currents, although in reality the axis orientation will represent the composite of the opposite responses to both polarities of stimulation (Mian and Day, 2009a). Measurement focused on the second peak of the SVS–force cross-covariance as it is of appropriate polarity and latency to reflect the GVS-evoked response studied in experiment 1.
Experiment 3
One possible factor responsible for an influence of stance width on response direction could be the change in mechanical state of the body. To establish whether this was critical, we examined the SVS-evoked response when light finger touch of an external surface was used to manipulate anisotropy of body stability instead of stance width. Light touch produces a reduction in body sway, which is more effective in the direction of the outstretched limb than perpendicular to it (Rabin et al., 1999). Therefore, light touch of a surface using an arm extended laterally can be expected to produce anisotropy in spontaneous body sway similar to that in increasing stance width. Following earlier studies, we defined light-touch contact as the application of <1 N of force (Holden et al., 1994; Rabin et al., 1999). Mechanical analysis indicates that this level of force applied at the fingertip provides negligible mechanical stabilization to the body (Holden et al., 1994). The reason for the anisotropic stabilizing effect of light touch is thought to be related to the richness of the proprioceptive input. Based on geometric considerations, for a given amount of body sway there would be greater joint configurational changes in the arm when the sway is in the direction of the arm than when it is perpendicular to it (Rabin et al., 1999). This represents a sensory advantage in the direction of the arm with greater potential to detect body sway.
The following two conditions were compared: (1) no touch; and (2) lateral light touch. In both conditions, stance width was 0 cm and the head-on-feet yaw angle was −45°. During the no-touch trials, the hands were held loosely by the side. In the light-touch condition, using the tip of the index finger of their right hand, participants lightly touched the surface of a small force plate (15.2 × 15.2 cm; HE6x6, AMTI) mounted on a secure heavy-duty tripod. The orientation of the plate was measured using the motion capture system, and forces were transformed into laboratory coordinates before analysis. As with the ground forces, the forces used in the analysis are the forces acting on the body (reaction forces). The surface of the force plate was positioned at the height of the umbilicus and laterally to the right of the participant such that a line in the horizontal plane from the midpoint of the two shoulders to the fingertip would be approximately parallel with the x-axis of the laboratory coordinate system. The distance from the participant was such that the inclusive angle between the upper arm and forearm, measured using a hand-held goniometer during initial positioning, was ∼150° (180° = straight arm). During trials, the positions of the shoulders and fingertip were recorded by the motion capture system. These recordings revealed that, in the horizontal plane, the line from the midpoint between the shoulders to the fingertip had an orientation of 5 ± 1° (group mean ± SD; i.e., approximately parallel with the x-axis) and a distance of 73 ± 4 cm.
Participants were told that they should touch the surface with sufficient force that their finger would not slide over the surface, but not to exceed 1 N of force. Before the start of each trial, a computer monitor in front of the participants provided feedback on the level of force being exerted on the platform. During the trials, when participants had their eyes closed, the experimenter monitored the level of force and instructed the participant to make adjustments if necessary.
Other than the use of light touch to influence stability, the experimental protocol was mostly the same as in experiment 2. The exception was that eight trials were collected per condition instead of six. Conditions were alternated from trial to trial, with the condition of the first trial chosen at random. Analysis was the same as that in experiment 2.
Unperturbed standing
Before the assessment of vestibularly evoked balance responses, at the start of each experiment we recorded the position of the C7 marker during quiet, unperturbed standing with eyes closed (30 s at each stance width or touch condition). In each experiment, apart from experiment 2b, participants adopted a −45° head yaw orientation. In experiment 2b, participants adopted a 0° head yaw orientation. A simple measure of body sway (the SDs of the X and Y velocities of the C7 marker) was calculated for each posture.
Statistical analysis
Directions and magnitudes of the measured response vectors were analyzed separately.
Response directions.
Descriptive statistics for response directions (e.g., means, variances, and 95% confidence intervals of the mean) used calculations designed specifically for circular data (Zar, 2010). The mean response directions are meaningful only when angles within a sample are not distributed randomly in all directions. Therefore, the mean response directions were calculated only when the Rayleigh test for uniformity [Zar, 2010 (p. 624)] reported p < 0.05, indicating nonuniformity. To test for differences in response direction between more than two stance widths (experiments 1 and 2a), ideally one would use a test equivalent to repeated-measures ANOVA that is designed to handle circular, instead of linear, data. To our knowledge, such a test does not exist. Therefore, we used a repeated-measures randomization test (Edgington and Onghena, 2007). To conduct the test, a bespoke effect statistic needs to be calculated that is suitable for the data and the hypothesis. We used between-stance-width circular variance of the mean response directions as the test statistic (an effect of stance width would produce significant variance in the mean response directions, while the absence of effect would produce near-zero variance). After calculating the statistic, the within-subject data were then randomly shuffled, independently for each participant, and the effect statistic was then calculated for the shuffled dataset. This was repeated 1999 times. Thus, there was one effect statistic calculated from the experimental data arrangement, and 1999 effect statistics were calculated from randomly arranged versions of the data. The p value of the test represents the proportion of permutations of the data that produce a larger effect statistic than that obtained from the actual arrangement of the experimental data. Comparisons between pairs of angles (experiment 3) used an established circular analog of the paired t test [i.e., the Hotelling paired angles test; Zar, 2010 (p. 652)].
To establish how early statistically significant differences in response directions occurred in experiment 1, the randomization test for force response directions was repeated every 5 ms between 0 and 1 s from stimulus onset. Because at each time point the test included only stance widths at which the Rayleigh test for uniformity reported p < 0.05, the number of stance widths included in the test could vary (from two to four) over time.
Linear measures.
The effects of stance width or touch on variables with linear scales (i.e., response magnitudes, SD of C7 sway during quiet standing, Sx/Sy ratios introduced in experiment 2b results) were assessed using ANOVA or t tests, depending on the number of factors and levels. In experiment 2b, independent samples tests were used, otherwise repeated/paired samples tests were used.
An α level of p = 0.05 was used as the threshold for statistical significance.
Results
Unperturbed standing
The effect of stance width on X and Y components of C7 sway during quiet standing is shown in Figure 2A using data from experiment 1. Increasing stance width led to a reduction in C7 sway (Fstance width = 14.8, p < 0.001). The effect was larger in the X direction (Fstance width × direction = 22.9, p < 0.001), as emphasized by plotting X/Y ratios (Fig. 2B). This effect of stance width was found to be the same in experiment 2 (data not shown).
Figure 2.
Body sway during quiet standing. Body sway is represented here as the SD of C7 velocity during quiet standing. A, C, Group mean sway measured in X and Y directions of the laboratory coordinate system (Lab). B, D, Group mean X/Y ratio for sway. Error bars represent 95% confidence intervals of the mean. The top row of panels (A, B) shows the effect of stance width using data from experiment 1. Labels on the abscissa denote the stance width in centimeters. The bottom row of panels (C, D) shows the effect of lateral touch (experiment 3).
In experiment 3, the mean ± SD magnitude (resultant of X, Y, and Z components) of touch force during quiet standing was 0.59 ± 0.25 N, confirming the touch was light. The effect of light touch on sway is shown in Figure 2, C and D. Similar to increasing stance width, lateral light touch led to a reduction in C7 sway during quiet standing (Ftouch = 49.3, p < 0.001) with the effect being larger in the X direction (Ftouch × direction = 32.5, p < 0.001), as emphasized by plotting X/Y ratios (Fig. 2D). These observations confirm that both increasing stance width and the use of light touch produced anisotropy in body stability.
Effect of stance width on GVS-evoked balance responses at 45° head yaw (experiment 1)
Figure 3 shows the GVS-evoked movement of C7 viewed from above. Although subsequent figures show polarity-collapsed data, Figure 3 shows the response to both stimulus polarities. As expected for this head angle, the body swayed diagonally. Figure 3 also shows qualitatively that the direction of body sway was affected by stance width. The C7 sway path was closest to diagonal for 0 cm stance width, and it rotated away from the more stable mediolateral (X) direction and toward the less stable anteroposterior (Y) direction as stance width increased. It is noticeable that the C7 response magnitudes in Figure 3 were larger for the forward-directed responses than the backward-directed responses. Why this occurred is not clear, but we suspect it is due to asymmetry in anterior–posterior balance control rather than in afferent responses to different stimulus polarities, because the asymmetry was not present in early force responses (data not shown). Nevertheless, the effect of stance width was equivalent for both polarities, supporting our decision to collapse across polarities.
Figure 3.
Effect of stance width on GVS-evoked movement of C7 at −45° head angle viewed from above. Data are from experiment 1. The plot shows the X and Y components of the group-averaged C7 position at each stance width between 0 and 2 s from stimulus onset. Traces have been forced to the origin at t = 0. Unlike other figures of the experiment 1 evoked response, both stimulus polarities are plotted (ARCL responses move in +X and −Y; ALCR responses move in −X and +Y). Dots represent position every 0.5 s.
Figure 4 shows the X and Y components of the group-averaged, polarity-collapsed C7 position plotted against time, as well as the group-averaged direction and magnitude at the end of the stimulation period (2 s). It can be seen from the time series that the X component is more affected by stance width than the Y component. The effect of stance width on both response direction (p < 0.001) and response magnitude (F = 9.41, p = 0.001) was statistically significant.
Figure 4.
Effect of stance width on GVS-evoked movement of C7 at −45° head angle. Polarity-collapsed data are from experiment 1. A, B, Group mean GVS-evoked C7x (A) and C7y (B) time series. Time is relative to GVS onset. C, D, Group mean response directions (C) and magnitudes (D) of C7 measured at 2 s. Error bars represent 95% confidence intervals of the mean. The shaded segment in C was formed from 95% confidence intervals of expected directions based solely on measured head yaw angles.
Figure 5 shows the X and Y components of the polarity-collapsed ground reaction force plotted against time, as well as the average direction and magnitude measured at a relatively early stage of the response (0.4 s). It can be seen from the time series that the X component is more affected by stance width than the Y component. The effect of stance width on both response direction (p < 0.001) and response magnitude (F = 22.1, p < 0.001) was statistically significant.
Figure 5.
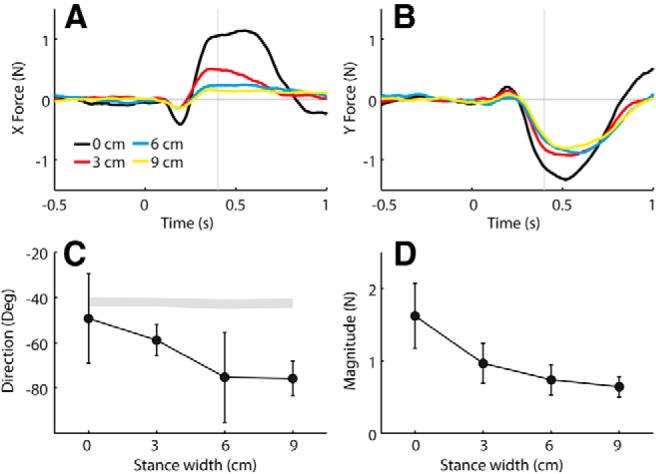
Effect of stance width on GVS-evoked force response at −45° head angle. Polarity-collapsed data are from experiment 1. A, B, Group mean GVS-evoked X force (A) and Y force (B) time series. Time is relative to GVS onset. C, D, Group mean response directions (C) and magnitudes (D) of force measured at 0.4 s. Error bars represent 95% confidence intervals of the mean. The shaded segment in C was formed from 95% confidence intervals of expected directions based solely on measured head yaw angles.
As will be elaborated on in the Discussion, it was of interest to establish how early stance width had a statistically significant effect on response direction as well as when the onset of body motion occurred. Within the period 0–1 s, a statistically significant effect of stance width on force response direction was apparent from 0.335 s and occurred at every time point until 0.700 s (p < 0.05). The mean ± SD onset of body motion determined from C7 speed was at 0.31 ± 0.09 s (0 cm stance width), 0.38 ± 0.32 s (3 cm stance width), 0.37 ± 0.17 s (6 cm stance width), and 0.36 ± 0.21 s (9 cm stance width) following stimulus onset.
Effect of stance width on SVS-evoked balance responses at 45° head yaw (experiment 2a)
Figure 6 shows the cross-covariance between SVS and the X and Y components of the force as well as the response directions and magnitudes derived from these data. Similar to the responses in experiment 1, the SVS–force cross-covariance was more affected in the X direction than in the Y direction. There was a significant effect of stance width on both response direction (p < 0.001) and magnitude (F = 17.6, p = 0.004). The overall mean ± SD latency of the second peak of the cross-covariance (i.e., the time of measurement of the direction and magnitude) was 0.377 ± 0.035 s, with no significant difference between stance widths (F = 0.74, p = 0.54).
Figure 6.
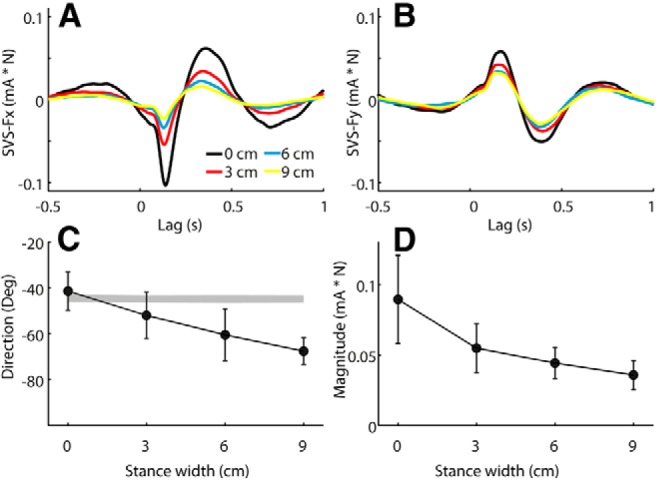
Effect of stance width on SVS-evoked response at −45° head angle. Data are from experiment 2a. A, B, Group mean SVS–X force (Fx; A) and SVS–Y force (Fy; B) cross-covariance. C, D, Group mean response directions (C) and magnitudes (D). Error bars represent 95% confidence intervals of the mean. The shaded segment in C was formed from 95% confidence intervals of expected directions based solely on measured head yaw angles.
Effect of stance width on relationship between head yaw and SVS-evoked balance responses (experiment 2b)
Figure 7 plots the group mean response direction against head yaw. At 0 cm stance width, the relationship between head and response direction was close to linear. At 6 cm stance width, there was a clear nonlinearity in the relationship similar to that shown in Figure 1B. Using the MATLAB (version 2012b, MathWorks) function nonlinearmodel.fit, we fit Equation 1 to the data, with c fixed to 0. The thicker solid line in Figure 7 depicts the fit to the plotted group mean response directions. When fitted to individual subjects, the 95% confidence intervals of the Sx/Sy ratios emerging from the fits were 1.11 ± 0.18 (0 cm stance width; i.e., close to linear) and 0.47 ± 0.15 (6 cm stance width; 0 vs 6 cm, t = 4.56, p < 0.001). It was also of interest to determine how closely this departure from craniocentricity could be predicted using X and Y components of our simple measure of baseline sway (Fig. 2) in place of Sx and Sy. We assume that body sway is a correlate of the degree of underlying instability. The 95% confidence interval of the X/Y ratios for baseline sway were 1.26 ± 0.20 (0 cm stance width) and 0.66 ± 0.10 (6 cm stance width). The resulting prediction is depicted as the thinner solid lines in Figure 7. These predictions using baseline sway capture the general form of the data; however, they tend to underestimate the measured departure from craniocentricity at 6 cm stance width when the X/Y sway ratio is <1 and overestimate it at 0 cm stance width when the X/Y sway ratio is >1.
Figure 7.
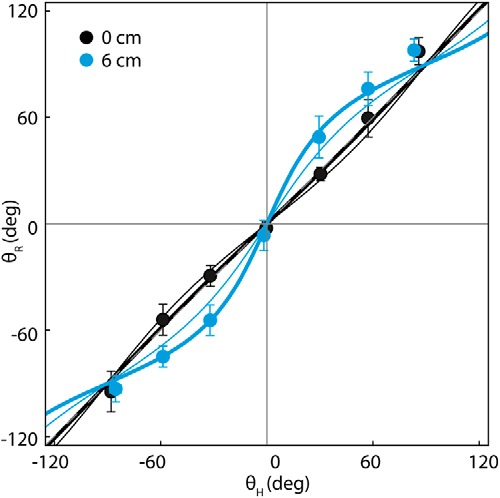
Relationship between head yaw and SVS-evoked response direction at 0 and 6 cm stance widths. Data are from experiment 2b. Measured θH values plotted on the abscissa and θR values plotted on ordinate (mean and 95% confidence intervals for the mean). A dashed gray line represents the line of identity (mostly occluded by the thick black line). The thick solid lines represent Equation 1 fitted to the group mean response directions using nonlinear regression, with c fixed at 0. The fitted Sx/Sy ratios for these lines are 1.04 (0 cm stance width, black) and 0.44 (6 cm stance width, blue). The thin solid lines represent responses predicted from Equation 1 using group mean baseline sway (SD of C7 velocity) for the parameters Sx and Sy. The group mean X/Y ratios for this measure of baseline sway are 1.26 (0 cm stance width) and 0.66 (6 cm stance width).
Effect of light touch on SVS-evoked balance responses at 45° head yaw (experiment 3)
The mean ± SD magnitude (resultant of X, Y, and Z components) of force exerted on the touch surface during SVS plus touch trials was 0.63 ± 0.11 N. This confirms that the touch was light. Figure 8 shows the cross-covariance between SVS and the X and Y components of the net force as well as the response directions and magnitudes derived from these data. Net force, defined as the sum of the ground and touch forces, was used for analysis as it was considered a more rigorous measure than ground force alone. Furthermore, the cross-covariance between SVS and touch force was negligible (i.e., the peak was 6% of peak SVS–ground cross-covariance), as was the difference between the SVS–ground force and SVS–net force cross-covariance (peak SVS–net force cross-covariance was 97% of peak SVS–ground force cross-covariance). Similar to the effect of stance width, the effect of lateral touch on the SVS-force cross-covariance was greater with X force than Y force (Fig. 8A,B). There was a significant effect of lateral touch on both response direction (Fig. 8C; F = 17.9, p < 0.001) and magnitude (Fig. 8D; t = 9.0, p < 0.001). The overall mean ± SD latency of the second peak of the cross-covariance was 0.378 ± 0.055 s, with no significant effect of light touch (t = 0.69, p = 0.50).
Figure 8.
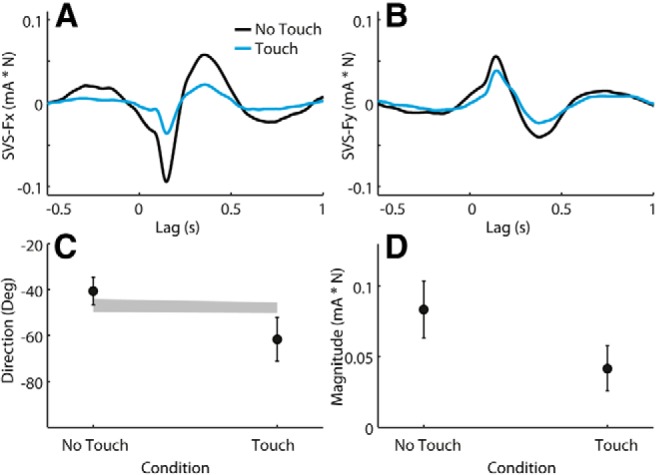
Effect of light touch on SVS-evoked response at −45° head angle. Data are from experiment 3. A, B, Mean SVS–X net force [NFx (ground plus touch platform); A] and SVS–NFy (B) cross-covariance (in milliAmperes per Newton). C, D, Group mean response directions (C) and magnitudes (D). Error bars represent 95% confidence intervals of the mean. The shaded segment in C was formed by joining 95% confidence intervals of expected directions based solely on measured head yaw angles.
Discussion
It is well established that the state of body stability influences the magnitude of the vestibularly evoked balance response (Day et al., 1997), indicating that the response is not a simple correction of the vestibular error signal. The current study extends this by showing that the response direction need not be aligned with the vestibular motion vector. Thus, anisotropic changes in body stability influence not just the magnitude but also the direction of the balance response. This implies that the balance system acts on components of vestibular signals to some extent independently in the frontal and sagittal planes.
State dependence of balance response directions
Earlier studies have considered directional properties of balance responses to other types of perturbation under conditions of anisotropic stability. For instance, there have been studies of responses to multidirectional platform perturbations at different stance widths (Henry et al., 1998, 2001; Jones et al., 2008) and a study of responses to leg muscle vibration when the support surface is made unstable in different directions (Ivanenko et al., 2000). An important distinction can be made between these studies and the current study. With mechanical perturbations, such as surface translation, stance width may influence the transmission from perturbation to sensory input, and unstable support surfaces may affect the primary afferent response to leg muscle vibration. In the current study, the afferent input due to the stimulus should be constant across conditions. It is only the state of the body that varies.
Two previous studies have reported states under which GVS-evoked balance responses deviated from craniocentricity. Gurfinkel' et al. (1989) reported that in some susceptible individuals maintenance of 90° head turn for several minutes led to an erroneous perceptual deviation of head position and a similar deviation in direction of the vestibularly evoked balance response. Ivanenko et al. (1999) reported that eccentric gaze led to bias in vestibularly evoked balance responses toward the direction of the gaze. These authors suggested that their findings indicated that spatial perception and visual reference systems, respectively, influenced vestibular spatial processing. It is likely that these phenomena arise from properties of the process that spatially transforms vestibular information from a head to a body reference frame. This is unlikely to be the case in the current study because a change in stance width or light touch would not influence this computation. It is not the calculation of head motion direction with respect to the feet that is affected by the change in stance width and touch, but rather how this information is used by the balance system.
Mechanical versus sensory factors
Increasing stance width alters the mechanical state of the body. The body attains a wider base of support and greater passive stability in the frontal plane. Furthermore, the mechanical advantage of the effectors is more affected in the frontal plane than in the sagittal plane. However, experiment 3 ruled out such factors as critical to the observed effect. Light touch has negligible mechanical stabilizing effect on the body (Holden et al., 1994) and does not mechanically alter the effectors, yet it had a potent effect on response direction. The effect was similar in size to that provided by increasing stance width from 0 to 6 cm (compare Figs. 6C, 8C). The anisotropic stabilizing effect of light touch is thought to be due to the greater sensitivity of proprioceptive feedback provided in the direction of the arm than perpendicular to it (Rabin et al., 1999). Similarly, increasing stance width also preferentially improves proprioceptive sensitivity in the frontal plane (Day et al., 1993). We suggest therefore that directional proprioceptive sensitivity is an important factor influencing the direction of the vestibularly evoked balance response. A possibility is that multisensory weighting is anisotropic, with the gain of the vestibularly evoked balance response being lower in the direction of higher proprioceptive sensitivity than in the orthogonal direction.
Role of feedback during the response
The preceding suggestion assumes the experimental manipulations affect the direction of the central motor command issued by the brain in response to the vestibular input. However, it is worth considering whether variation in response direction is a secondary effect from sensory feedback of the vestibularly driven reflex rather than the result of an altered motor command. Specifically, as the motor response to the artificial vestibular input develops, reafferent feedback from the movement will act to prevent the response from causing a real loss of balance (Day and Guerraz, 2007). It may be that higher proprioceptive sensitivity in the frontal plane leads to earlier attenuation of the response in that plane, causing the apparent bias in the response toward the anteroposterior direction. We suspect that feedback effects like this may well contribute late in the response. Is there evidence that the altered response direction manifests before feedback processes have had time to contribute?
To address this question, we focus on experiment 1. To our knowledge, the only systematic study of the temporal properties of feedback influence on the GVS-evoked balance response is the one by Day and Guerraz (2007). They demonstrated that feedback from visual self-motion does not influence the GVS-evoked response until after 400 ms. Certainly at this time point in the current study, the GVS-evoked response was clearly affected by stance width (Fig. 5). However, our subjects had their eyes closed, and so any relevant feedback process will arise from nonvisual sources. We found that there were statistically significant differences in the GVS-evoked response direction as early as 335 ms. If this were driven entirely by reafferent feedback, balance-relevant motion would need to have been detected at an earlier time to accommodate a reflex loop and an electromechanical delay. If we consider the patellar tendon reflex latency (∼20 ms; Frijns et al., 1997) as the shortest possible relevant loop time, and an electromechanical delay of ∼50 ms (Cavanagh and Komi, 1979), motion would need to have been detected by 265 ms (335 − 20 − 50 ms). At this time, the speed of the body was still within the baseline noise level (onset of C7 motion, experiment 1 in Results). In reality, a loop time of ∼70 ms may be more appropriate for a feedback-driven response as measured from early responses to whole-body mechanical perturbation in free-standing individuals (Horak and Nashner, 1986). This would place the requirement for the detection of body motion even earlier (215 ms). Therefore, it seems unlikely that processes related to response-evoked reafference could entirely explain the observed effect on response direction.
Model of the response direction effect
Across a wide range of head orientations, we demonstrated that the vestibularly evoked balance response direction could be reasonably well described with a simple model that gave differential weighting to the frontal and sagittal components of the vestibular error signal (Eq. 1). Fitting the model to the response indicated greater weighting of the component acting in the direction of lesser stability (Sy > Sx at the wider stance width).
In addition to estimating weighting factors from the response, we checked whether the response directions could be predicted when the weighting factors were represented using a simple measure of baseline body sway, which we assumed reflected the degree of baseline instability in each direction. At the wide stance width, this led to better prediction of the response direction than head orientation alone. However, it was not completely adequate for precise prediction, which may require a more complex, perhaps multifactorial, measure of the state of the body.
An aspect of the model worth emphasizing is that as stance width is increased, the direction of the vestibularly evoked balance response becomes biased toward the less stable sagittal plane, only when the vestibular signal contains components in both the frontal and sagittal planes of the body. When the vestibular signal contains only components that are in either the sagittal or frontal plane (i.e., −90°, 0°, and +90° head angles), there is no expectation of a difference in response direction between stance widths (Fig. 7).
Practical implications and conclusions
The findings of this study have methodological and clinical implications. When the stimulus-evoked vestibular error signal is not aligned with the sagittal or frontal planes, assessment of the vestibularly evoked balance response should control for directional bias in body stability. Under normal circumstances, this simply means controlling for stance width. However, some patients present with abnormal directionally specific body sway (Diener et al., 1984). Departure from the craniocentricity of the vestibularly evoked balance response in such patients may not necessarily indicate abnormal coordinate transformation of the vestibular signal, since it may be entirely appropriate for their underlying directional bias in body stability.
In conclusion, the direction of the balance response to electrical vestibular stimulation is state dependent, and a strictly craniocentric view of vestibularly evoked balance responses is inadequate. The balance system appears to assign different degrees of relevance to components of vestibular input signaling head motion in sagittal and coronal planes of the body, leading to different strengths of vestibulomotor coupling in those planes. This directional gain control may relate to body stability, but it is necessary to examine this hypothesis further and to investigate whether other factors play a role.
Footnotes
The work was funded by the UK Medical Research Council and the Wellcome Trust. We thank Daniel Voyce for technical support, and Amy Peters for assistance with data collection.
The authors declare no competing financial interests.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/3.0), which permits unrestricted use, distribution and reproduction in any medium provided that the original work is properly attributed.
References
- Britton TC, Day BL, Brown P, Rothwell JC, Thompson PD, Marsden CD. Postural electromyographic responses in the arm and leg following galvanic vestibular stimulation in man. Exp Brain Res. 1993;94:143–151. doi: 10.1007/BF00230477. [DOI] [PubMed] [Google Scholar]
- Cavanagh PR, Komi PV. Electromechanical delay in human skeletal muscle under concentric and eccentric contractions. Eur J Appl Physiol Occup Physiol. 1979;42:159–163. doi: 10.1007/BF00431022. [DOI] [PubMed] [Google Scholar]
- Dakin CJ, Son GM, Inglis JT, Blouin JS. Frequency response of human vestibular reflexes characterized by stochastic stimuli. J Physiol. 2007;583:1117–1127. doi: 10.1113/jphysiol.2007.133264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day BL, Fitzpatrick RC. Virtual head rotation reveals a process of route reconstruction from human vestibular signals. J Physiol. 2005;567:591–597. doi: 10.1113/jphysiol.2005.092544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day BL, Guerraz M. Feedforward versus feedback modulation of human vestibular-evoked balance responses by visual self-motion information. J Physiol. 2007;582:153–161. doi: 10.1113/jphysiol.2007.132092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day BL, Steiger MJ, Thompson PD, Marsden CD. Effect of vision and stance width on human body motion when standing: implications for afferent control of lateral sway. J Physiol. 1993;469:479–499. doi: 10.1113/jphysiol.1993.sp019824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day BL, Séverac Cauquil A, Bartolomei L, Pastor MA, Lyon IN. Human body-segment tilts induced by galvanic stimulation: a vestibularly driven balance protection mechanism. J Physiol. 1997;500:661–672. doi: 10.1113/jphysiol.1997.sp022051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diener HC, Dichgans J, Bacher M, Gompf B. Quantification of postural sway in normals and patients with cerebellar diseases. Electroencephalogr Clin Neurophysiol. 1984;57:134–142. doi: 10.1016/0013-4694(84)90172-X. [DOI] [PubMed] [Google Scholar]
- Edgington ES, Onghena P. Randomization tests. Boca Raton, FL: Chapman and Hall; 2007. [Google Scholar]
- Fitzpatrick RC, Day BL. Probing the human vestibular system with galvanic stimulation. J Appl Physiol. 2004;96:2301–2316. doi: 10.1152/japplphysiol.00008.2004. [DOI] [PubMed] [Google Scholar]
- Fitzpatrick R, Burke D, Gandevia SC. Task-dependent reflex responses and movement illusions evoked by galvanic vestibular stimulation in standing humans. J Physiol. 1994;478:363–372. doi: 10.1113/jphysiol.1994.sp020257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frijns CJ, Laman DM, van Duijn MA, van Duijn H. Normal values of patellar and ankle tendon reflex latencies. Clin Neurol Neurosurg. 1997;99:31–36. doi: 10.1016/S0303-8467(96)00593-8. [DOI] [PubMed] [Google Scholar]
- Gurfinkel' VS, Popov KE, Smetanin BN, Shlykov VY. Changes in the direction of vestibulomotor response in the course of adaptation to protracted static head turning in man. Neurophysiology. 1989;21:159–164. doi: 10.1007/BF01056975. [DOI] [PubMed] [Google Scholar]
- Halliday DM, Rosenberg JR, Amjad AM, Breeze P, Conway BA, Farmer SF. A framework for the analysis of mixed time series/point process data—theory and application to the study of physiological tremor, single motor unit discharges and electromyograms. Prog Biophys Mol Biol. 1995;64:237–278. doi: 10.1016/S0079-6107(96)00009-0. [DOI] [PubMed] [Google Scholar]
- Henry SM, Fung J, Horak FB. EMG responses to maintain stance during multidirectional surface translations. J Neurophysiol. 1998;80:1939–1950. doi: 10.1152/jn.1998.80.4.1939. [DOI] [PubMed] [Google Scholar]
- Henry SM, Fung J, Horak FB. Effect of stance width on multidirectional postural responses. J Neurophysiol. 2001;85:559–570. doi: 10.1152/jn.2001.85.2.559. [DOI] [PubMed] [Google Scholar]
- Hlavacka F, Njiokiktjien C. Postural responses evoked by sinusoidal galvanic stimulation of the labyrinth. Influence of head position. Acta Otolaryngol. 1985;99:107–112. doi: 10.3109/00016488509119152. [DOI] [PubMed] [Google Scholar]
- Holden M, Ventura J, Lackner JR. Stabilization of posture by precision contact of the index finger. J Vestib Res. 1994;4:285–301. [PubMed] [Google Scholar]
- Horak FB, Hlavacka F. Somatosensory loss increases vestibulospinal sensitivity. J Neurophysiol. 2001;86:575–585. doi: 10.1152/jn.2001.86.2.575. [DOI] [PubMed] [Google Scholar]
- Horak FB, Nashner LM. Central programming of postural movements: adaptation to altered support-surface configurations. J Neurophysiol. 1986;55:1369–1381. doi: 10.1152/jn.1986.55.6.1369. [DOI] [PubMed] [Google Scholar]
- Ivanenko YP, Grasso R, Lacquaniti F. Effect of gaze on postural responses to neck proprioceptive and vestibular stimulation in humans. J Physiol. 1999;519:301–314. doi: 10.1111/j.1469-7793.1999.0301o.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanenko YP, Solopova IA, Levik YS. The direction of postural instability affects postural reactions to ankle muscle vibration in humans. Neurosci Lett. 2000;292:103–106. doi: 10.1016/S0304-3940(00)01438-5. [DOI] [PubMed] [Google Scholar]
- Jones SL, Henry SM, Raasch CC, Hitt JR, Bunn JY. Responses to multi-directional surface translations involve redistribution of proximal versus distal strategies to maintain upright posture. Exp Brain Res. 2008;187:407–417. doi: 10.1007/s00221-008-1312-1. [DOI] [PubMed] [Google Scholar]
- Lund S, Broberg C. Effects of different head positions on postural sway in man induced by a reproducible vestibular error signal. Acta Physiol Scand. 1983;117:307–309. doi: 10.1111/j.1748-1716.1983.tb07212.x. [DOI] [PubMed] [Google Scholar]
- Mian OS, Day BL. Determining the direction of vestibular-evoked balance responses using stochastic vestibular stimulation. J Physiol. 2009a;587:2869–2873. doi: 10.1113/jphysiol.2009.171256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mian OS, Day BL. Directional properties of the short-latency vestibular evoked balance response. Paper presented at ISPGR XIX Satellite Pre-Conference; June; Pavia, Italy. 2009b. [Google Scholar]
- Pastor MA, Day BL, Marsden CD. Vestibular induced postural responses in Parkinson's disease. Brain. 1993;116:1177–1190. doi: 10.1093/brain/116.5.1177. [DOI] [PubMed] [Google Scholar]
- Rabin E, Bortolami SB, DiZio P, Lackner JR. Haptic stabilization of posture: changes in arm proprioception and cutaneous feedback for different arm orientations. J Neurophysiol. 1999;82:3541–3549. doi: 10.1152/jn.1999.82.6.3541. [DOI] [PubMed] [Google Scholar]
- Welgampola MS, Colebatch JG. Vestibulospinal reflexes: quantitative effects of sensory feedback and postural task. Exp Brain Res. 2001;139:345–353. doi: 10.1007/s002210100754. [DOI] [PubMed] [Google Scholar]
- Zar JH. Biostatistical analysis. Ed 5. Upper Saddle River, NJ: Pearson Education; 2010. [Google Scholar]