Figure 1.

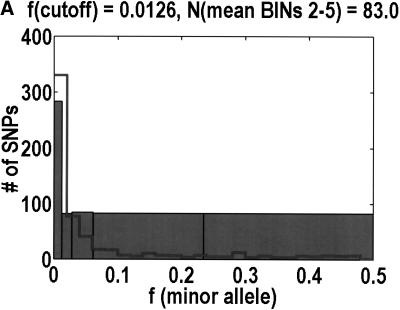
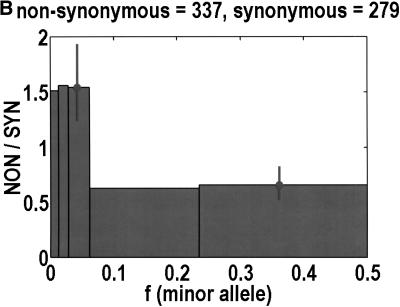
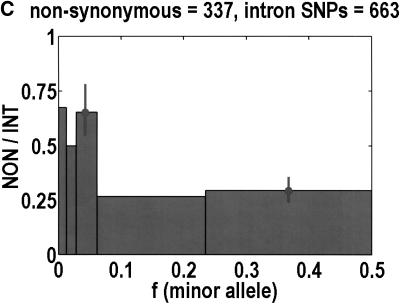
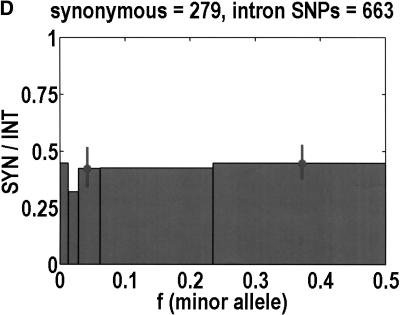
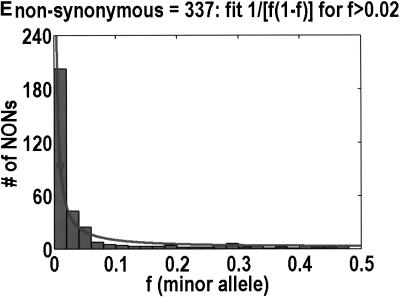
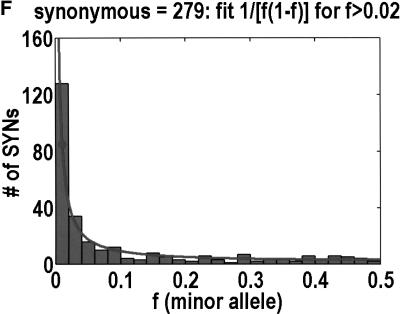
To analyze ratios for the number of SNPs that are deemed nonsynonymous (NON), synonymous (SYN), and intron (INT), we partition the frequency axes into 5 nonuniform bins with boundaries 0.0000, 0.0126, 0.0280, 0.0614, 0.2346, and 0.5000. There are 284 coding SNPs in bin 1, and there is a mean of 83.0 coding SNPs in each of the bins 2–5. These panels depict (A) the number of coding SNPs, with a solid line for the same data plotted on a uniform bin size of 0.02, (B) the NON/SYN ratio, (C) the NON/INT ratio, and (D) the SYN/INT ratio. Error bars indicate standard deviation, assuming the data are sampled from a binomial distribution. All of the uncertainty is in bins 2–5. Error bars for bin 1 are much smaller and not indicated. The generally lower quality of the intron data is responsible for the glitch in bin 2 of panels C and D. At top of each panel, we indicate the number of SNPs in the stated categories. Finally, we demonstrate the futility of trying to make sense of these data by more conventional methods. Using a uniform bin size of 0.02, we plot the number of (E) NON and (F) SYN polymorphisms, and compare them with the neutral theory expectation of 1/[f(1-f)]. Our curve fitting procedures ignore the first bin to avoid the singlets and sampling uncertainties. Extrapolation of the curve fit back to the first bin is indicated by a filled circle. Only if one squints hard enough at the fit deviations, might one notice a change in NON/SYN ratio.