An Approach to Rapid Calculation of Temperature Change in Tissue Using Spatial Filters to Approximate Effects of Thermal Conduction

Abstract

We present an approach to performing rapid calculations of temperature within tissue by interleaving, at regular time intervals, 1) an analytical solution to the Pennes (or other desired) bioheat equation excluding the term for thermal conduction and 2) application of a spatial filter to approximate the effects of thermal conduction. Here, the basic approach is presented with attention to filter design. The method is applied to a few different cases relevant to magnetic resonance imaging, and results are compared to those from a full finite-difference (FD) implementation of the Pennes bio-heat equation. It is seen that results of the proposed method are in reasonable agreement with those of the FD approach, with about 15% difference in the calculated maximum temperature increase, but are calculated in a fraction of the time, requiring less than 2% of the calculation time for the FD approach in the cases evaluated.

I. Introduction

In a number of biomedical applications, a change in the energy deposition throughout the body can lead to a change in the temperature distribution. In many cases, it is advantageous to predict the temperature change from estimates of the energy distribution in order to assure, depending on the particular application, that a desired temperature distribution is achieved [1]–[3] or that no tissues will be heated excessively [4]–[6].

Currently in magnetic resonance imaging (MRI), there is great interest in performing case-specific safety evaluations very rapidly. This is in part due to the development of transmit arrays in MRI [7], facilitating an infinite variety of possible desired radiofrequency (RF) magnetic field patterns and associated RF heating patterns in each individual patient. One major challenge to real-time case-specific safety predictions is accurate prediction of the heating pattern, or specific energy absorption rate (SAR) distribution in the subject. While there are a variety of approaches to calculating [8], [9] or measuring [10], [11] this pattern with increasing speed, another obstacle is the interpretation of the SAR distribution for purposes of ensuring safety. Although exposure to increased temperature over time is more easily correlated with potential damage to tissue [12], due in part to complexities and time requirements for calculating temperature, a spatially averaged SAR value, often averaged over 10 g regions (SAR_10g ), is used much more commonly in safety evaluations.

Recently, methods to rapidly compute temperature increase for biomedical applications have been included [13]–[15]: a hybrid alternating-direction implicit (ADI) approach to solving the heat equation for a heterogeneous numerical model [13], a method of superposition from separate sources combined with model simplification [14], and a semianalytical Fourier-based solution for simple 3-D geometry [15]. Here, we present a new accelerated approach to solving the Pennes (or other) bioheat equation. Recognizing that thermal conduction—the most computationally intensive portion of models for heat transfer in biological samples—has the effect of smoothing or blurring the temperature distribution in space, we approximate the effects of thermal conduction with a low-pass spatial filter applied to the temperature distribution at regular time intervals. The method produces reasonably accurate results much more quickly than the more commonly used finite-difference (FD) approach to calculating temperature, and even more quickly than calculation of complete SAR_10g distribution. It is hoped that this approach will be useful in rapid production of meaningful evaluations of heat induced during MRI and other applications in the future.

II. Method

A. Temperature Computation

The relationship between temperature T and the applied energy distribution is often described with Pennes’ bioheat equation [16]

$$\rho c_h\frac{\partial T}{\partial t}=\nabla ·(k\nabla T)-W_{{\rho }_{\text{bl}}{c}_{h\text{bl}}}(T-T_{\text{bl}})+Q+\rho \text{SAR}$$ (1)

where c_h is the heat capacity, W is the blood perfusion rate, k is the thermal conductivity, ρ is the tissue mass density, the subscript _bl indicates values for blood, Q is the heat generated by metabolism, and SAR is the specific energy absorption rate (W per kg of tissue) resulting from some heating source. For example, in the case of RF electromagnetic field with rms electric field E

$$\text{SAR}=\frac{\sigma {\mid E\mid }^2}{\rho }$$ (2)

where σ is the electrical conductivity.

While Pennes’ bioheat equation has its limitations, it is often used as a good first-order approximation for temperature in tissue. The largest computational challenge to applying (1) is the time required to accurately calculate the thermal conduction of heat, represented by the first term on the right-hand side of the equation.

Separating T in (1) into an initial equilibrium temperature T₀ when SAR is zero and a time-dependent increased temperature T_i after perturbation with a nonzero SAR such that T = T₀ + T_i, we can write

$$\rho c_h\frac{\partial T_0}{\partial t}+\rho c_h\frac{\partial T_i}{\partial t}=\nabla ·(k\nabla T_0)+\nabla ·(k\nabla T_i)-W{\rho }_{\text{bl}}{c}_{h\text{bl}}(T_0-T_{\text{bl}})-W{\rho }_{\text{bl}}{c}_{h\text{bl}}{T}_i+Q+\rho \text{SAR}$$ (3)

and

$$\rho c_h\frac{\partial T_0}{\partial t}=\nabla ·(k\nabla T_0)-W{\rho }_{\mathrm{b}1}{c}_{h\mathrm{b}1}(T_0-T_{\mathrm{b}10})+Q_0.$$ (4)

Subtracting (4) from (3) produces

$$\rho c_h\frac{\partial T_i}{\partial t}=\nabla ·(k\nabla T_i)-W{\rho }_{\text{bl}}{c}_{h\text{bl}}(T_i)+\rho \text{SAR}+\mathrm{\Delta }Q+W{\rho }_{\text{bl}}{c}_{h\text{bl}}\mathrm{\Delta }{T}_{\text{bl}}$$ (5)

where Q = Q₀ + ΔQ and T_bl = T_bl0 + ΔT_bl and where, for the linearity of (5), ΔQ and ΔT_bl can be considered as an additional heat sources (or sinks, depending on the sign of these terms) like SAR.

If absolute temperature (rather than just temperature change) is desired, T₀ needs to be calculated only once for a given biological sample with any desired method, such as a full FD implementation of (1) [4]. Conceivably, experimentally measured data could also be used to provide the initial equilibrium temperature distribution. Depending on the application, it may be necessary to calculate only the temperature increase above T₀ (i.e., T_i ) in which case only (5) is needed. Using a similar approach, we can also consider the increase in temperature in multiple stages or intervals n such that T_{n + 1} = T_n + ΔT_n where ΔT_n is the temperature increase during the n^th time interval.

With our proposed approach, T_i over time is calculated by applying a spatial filter at regular intervals t_int to approximate effects of thermal conduction (the first term on the right-hand side of (5)) and calculating the effects of the remaining terms in (5) over the same intervals analytically. If the thermal conduction term is removed from (5), what remains is a first-order linear ordinary differential equation

$$T_{n+1}=\frac{\rho \text{SAR}+\mathrm{\Delta }Q+W{\rho }_{\text{bl}}{c}_{h\text{bl}}\mathrm{\Delta }{T}_{\text{bl}}}{W{c}_{\text{bl}}{\rho }_{\text{bl}}}\left(1-e^{-\frac{W{c}_{h\text{bl}}{\rho }_{\text{bl}}}{c_h\rho }{t}_{int}}\right)+T_n{e}^{-\frac{W{c}_{h\text{bl}}{\rho }_{\text{bl}}}{c_h\rho }{t}_{int}}$$ (6)

and can be solved directly. Importantly, all paramaters in this equation (especially ΔQ, ΔT_bl, and W) can be considered functions of time or local temperature and updated according to additional considerations, such as thermoregulation [6].

To design an effective spatial filter for accurately approximating the effects of thermal conduction, we selected an approach considering the poles of a 3-D low-pass filter

$$F({\lambda }_x,{\lambda }_y,{\lambda }_z)=\frac{1}{{\left(1+\frac{i{\lambda }_x}{p_{x1}}\right)}^{{\alpha }_{x1}}{\left(1+\frac{i{\lambda }_x}{p_{x2}}\right)}^{{\alpha }_{x2}}{\left(1+\frac{i{\lambda }_y}{p_{y1}}\right)}^{{\alpha }_{y1}}}·\frac{1}{{\left(1+\frac{i{\lambda }_y}{p_{y2}}\right)}^{{\alpha }_{y2}}{\left(1+\frac{i{\lambda }_z}{p_{z1}}\right)}^{{\alpha }_{z1}}{\left(1+\frac{i{\lambda }_z}{p_{z2}}\right)}^{{\alpha }_{z2}}}$$ (7)

where λ_x, λ_y, and λ_z are the spatial variables in the Fourier domain corresponding to x, y, and z directions, respectively; p_x1, p_{y 1}, and p_{z 1} are the first (low) cutoff frequencies for the spatial variables λ_x, λ_y, λ_z ; and p_x2, p_y2, and p_z2 the second (high) cutoff frequencies in the Fourier directions. Two cutoff frequencies in each direction have been chosen, due to the spatial second derivative dependence of heat conductivity in (5). In addition, α_x1, α_y1, and α_z1 are the orders of the first cutoff frequencies, and α_x2, α_y2, and α_z2 the orders of the second cutoff frequencies. The parameters α and p change according to the user-selected time interval t_int.

Using the properties of the Fast Fourier Transform (FFT), the cutoff frequencies in (7) can be scaled appropriately for the size of the meshgrid (dimensions of the sample space in grid cells) and meshgrid dimensions (size of a single cell in meters). In fact, the cutoff frequency is proportional to the size of the meshgrid and to the meshgrid dimensions. For example, if we indicate with M_{m ×n ×p} the size of the meshgrid containing the sample, and with a, b, and c the dimensions of the grid in the x, y, and z directions

$$\begin{array}{l}{p}_{x1}=p_{x1s}\frac{ma}{m_s{a}_s}\\ p_{x2}=p_{x2s}\frac{ma}{m_s{a}_s}\\ p_{y1}=p_{y1s}\frac{nb}{n_s{b}_s}\\ p_{y2}=p_{y2s}\frac{nb}{n_s{b}_s}\\ p_{z1}=p_{z1s}\frac{pc}{p_s{c}_s}\\ p_{z2}=p_{z2s}\frac{pc}{p_s{c}_s}\end{array}$$ (8)

where p_x1s, p_x2s, p_y1s, p_y2s, p_z1s, and p_z2s are the computed optimum cutoff frequencies for starting matrix M_s of dimensions m_s × n_s × p_s (M_sms,ns,ps) with meshgrid resolution a_s × b_s × c_s.

In this study, the optimal values for all cutoff frequencies p and orders α were determined for three different time intervals t_int (30, 60, and 120, s) using a conjugate gradient method to minimize the sum of the square of the difference in temperature between the result applying the filter and that calculated using an FD solution of (1) [8] for a box-shaped sample of water at 2 mm × 2 mm × 2 mm resolution and an SAR distribution determined numerically using commercial software (XFDTD, Remcom Inc., State College, PA) for the sample in a birdcage coil for MRI at 125 MHz. Details of the model and validation of the full FD heating pattern with comparison to experiment have been published previously [17]. In the determination of SAR, the sample was assigned an electrical conductivity of 1.895 S/m, and a relative electric permittivity of 78.

After the optimal parameters were determined, the ability to scale them according to mesh spatial resolution as in (8) was tested with a variety of applications in comparison to a full FD representation of (1). These included a human head in a quadrature surface coil for MRI at 300 MHz [8] and a human head with a 5 mm focal heating source in brain, as might more be pertinent in a model for ablation.

Starting from the temperature distribution T_n = T₀, the procedure to apply the method can be summarized as the application of following.

• Step 1: the solution given in (6) of the analytical equation (5) without the heat conductivity term.

• Step 2: computation of the FFT of the temperature distribution T_{n + 1}.

• Step 3: application of the filter in (7).

• Step 4: computation of the inverse FFT.

The procedure is repeated until the total heating time is computed, defining T_n as the solution of the inverse FFT (Step 4) at the end of each repetition.

B. SAR_10g Computation

To compare temperature distributions to the corresponding SAR_10g distributions, we utilized a previously presented method for calculating SAR_10g [20], [21]. The algorithm sequentially increases the radius of a spherical mask centered on the voxel of interest. The mass and the summed SAR of all the voxels in both the most external layer and the interior volume are calculated. When the total mass (external layer plus inner ones) exceeds 10 g, the SAR of the external layer is weighted to reach the desired 10 g mass. Indicating with m_s and m_i the mass in grams of the surface and interior portions, respectively, SAR_s and SAR_i the sum of the SAR values in the external and internal layers respectively, and n_s and n_i the number of pixels in the external and internal layers, the SAR_10g is calculated as

$${\text{SAR}}_{10g}=\frac{\left(\frac{10g-m_i}{m_s}\right){\text{SAR}}_s+{\text{SAR}}_i}{\left(\frac{10g-m_i}{m_s}\right)n_s+n_i}.$$ (9)

III. Results

Table I provides the empirically determined optimal values for the filter parameters on a matrix of 250 cells in each dimension (M_{s250, 250, 250}) with a resolution of 2 mm in each dimension (a_s = b_s = c_s = 2 mm) and for a variety of time intervals. As discussed previously, cutoff frequencies p for (7) can easily be determined for other sample sizes and grid resolutions (8) and the orders α for (7) are independent of these parameters, but the optimal values must be determined for each time interval independently.

TABLE I.

Optimum Filter Parameters

Parameters	tint = 30s	tint = 60s	tint = 120s
px1s, py1s, pz1s	20.56	15.12	6.32
px2s, py2s, pz2s	52.01	28.53	23.26
αx1s, αy1s, αz1s	0.37	0.18	0.08
αx2s, αy2s, αz2s	0.67	1.05	1.27

Optimum filter parameter values for a sample matrix M_{s250, 250, 250} with a meshgrid resolution of 2 mm × 2 mm × 2 mm.

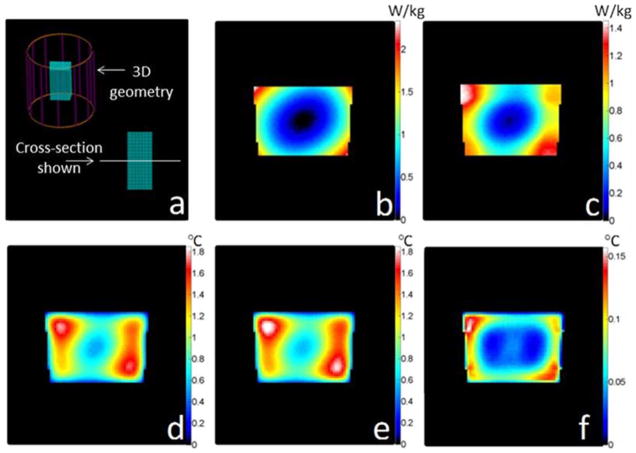
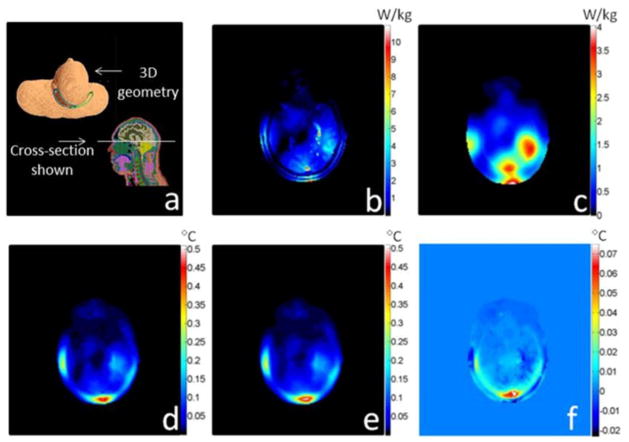
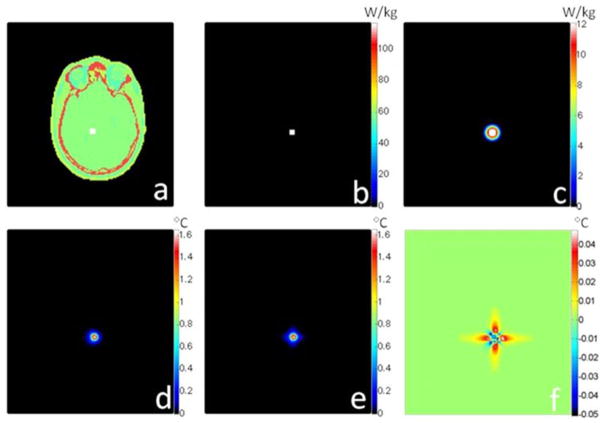
Fig. 1 presents the results for the case of a gelatinous phantom exposed to an SAR distribution as induced by a birdcage-type MRI coil [17] designed for imaging of the human head. Figs. 2 and 3 similarly present the geometry and results for the case of a human head exposed to an SAR distribution induced by a quadrature surface coil for MRI [8], and a point source of heat deep within brain tissue (more relevant for local ablation than MRI), respectively. The material properties used for the cases of the head model are reported in Table II. In each of these three figures, the unaveraged SAR, SAR_10g, temperature increases as calculated with the full FD and proposed methods, and the differences between these last two are presented. For each case shown here, the time required to calculate temperature with the proposed method was tens of seconds depending on the meshgrid resolution, matrix size, and total heating time for a 3 GHz central processing unit (CPU) with 4 GB of random access memory (RAM). The computation time is less than 2% of that required to calculate temperature with the full FD method and less than 10% of that required to calculate SAR_10g (see Figs. 1–3).

Fig. 1.

For a box of water-based gel, plots of (a) geometry of the problem with the box in a birdcage coil operating at 125 MHz, (b) the unaveraged SAR distribution, (c) 10 g average SAR distribution(1 min computation time), (d) temperature increase calculated with a rigorous FD algorithm (15 min heating time, 6 min computation time), (e) temperature increase calculated with the proposed rapid algorithm (15 min heating time, 5 s computation time), and (f) difference between the full FD method and the proposed method. The chosen time interval is t_int = 30 s, the meshgrid resolution is 2 mm × 2 mm × 2 mm, and the matrix size is 80 × 80 × 80 cells.

Fig. 2.

For a human head model, plots of (a) geometry of the problem with the head in a quadrature surface coil operating at 125 MHz, (b) unaveraged SAR distribution, (c) 10 g average SAR distribution(4 min computation time), (d) temperature increase calculated with a rigorous FD algorithm (15 min heating time, 23 min computation time), (e) temperature increase calculated with the proposed rapid algorithm (15 min heating time, 25 s computation time), and (f) the difference between the full FD method and the proposed method. The chosen time interval is t_int = 30 s, the meshgrid resolution is 2 mm × 2 mm × 2 mm, and the matrix size is 150 × 140 × 120 cells.

Fig. 3.

For a human head model, plots of (a) geometry of the problem showing the heat source (white box) within the head (the 3-D geometry and the cross section are the same as Fig. 2), (b) unaveraged SAR distribution, (c) 10 g average SAR distribution(4 min computation time), (d) temperature increase calculated with a rigorous FD algorithm (15 min heating time, 23 min computation time), (e) temperature increase calculated with the proposed rapid digital filter algorithm (15 min heating time, 25 s computation time), and (f) difference maps between the full FD method and the proposed method. The chosen time interval is t_int = 30 s, the meshgrid resolution is 2 mm × 2 mm × 2 mm, and the matrix size is 150 × 140 × 120 cells.

TABLE II.

Material Properties of the Body Tissues

Tissue	W(m1/min/kg)	ρ(kg/m3)	cn(J/kg/C°)	k(W/m/C°)	Q(W/kg)
Blood	10000	1050	3617	0.52	0
Cancellous bone	30	1178	2274	0.31	0.46
Cartilage	35	1100	3568	0.49	0.54
Cerebellum	770	1045	3653	0.51	15.67
Cortical bone	10	1908	1313	0.32	0.15
CSF	0	1007	4096	0.57	0
Fat	33	911	2348	0.21	0.51
Grey Matter	763	1045	3696	0.55	15.53
Muscle	39	1090	3421	0.49	0.96
Nerve	160	1075	3613	0.49	2.48
Sclera	380	1032	4200	0.58	5.89
Skin	106	1109	3391	0.37	1.65
Tendon	29	1142	3432	0.47	0.45
Tongue	78	1090	3421	0.49	1.21
Vitreous humor	0	1005	4047	0.59	0
White Matter	213	1041	3583	0.48	4.34

Material properties of the body tissues.

IV. Discussion

The distribution of temperature increase resulting from the application of heat in vivo is a function of many factors that can be considered dependent on temperature and/or environment, including rates of blood perfusion and metabolism throughout the body and rates of perspiration and radiation at the surface of the body [5], [6]. Additionally, the directionality of blood flow through a heat field adds significant complexity, especially near blood vessels [18], [19].

Any accurate prediction of temperature in vivo must consider effects of thermal conduction. In the Pennes bioheat equation (a well-known, relatively simple formula for calculating temperature), the term for heat conduction is the most complex and difficult to calculate. Here, we have shown that approximating the effects of this term with a spatial filter can greatly accelerate the calculation of temperature increase while still producing reasonable results when compared to a full FD approach. Success of this approach stems, in part, from the fact that thermal conductivity in human tissues, in comparison to perfusion rates and rates of metabolism, are relatively homogeneous [8]. While the application of the spatial filter approximation used here was to the Pennes bioheat equation, in principle it could be integrated into more sophisticated representations to accelerate the estimation of thermal conduction effects.

In the applications presented here, two are related to assessing the amount of RF heating occurring during an MRI exam (see Figs. 1 and 2) and one is more closely related to localized ablation (see Fig. 3). In the case of a nonperfused imaging phantom within an MRI coil (see Fig. 1), the proposed method gives results within about 0.15 °C of the full FD calculation, or within about 8% of the maximum temperature increase. In the case of a perfused human head within an MRI coil (see Fig. 2), the proposed method gives results within about 0.075 °C of the full FD calculation, or within about 15% of the maximum temperature increase. In both of these cases, the proposed method overestimates the maximum temperature increase, which would provide a more conservative estimate for safety assurance. In the case of a perfused human head with a local heat source deep in the brain (see Fig. 3), the proposed method gives results within about 0.05 °C of the full FD calculation, or within about 3% of the maximum temperature increase. In this case, the proposed method underestimates and overestimates temperature increase by nearly equal amounts and in nearly equal volumes throughout space. The amount of relative error in the case of the local source deep in brain is lowest because here the greatest amount of heating occurs at a location surrounded by tissue with fairly homogeneous thermal conductivity. The case of the human head in the MRI coil has the largest relative error because the location of greatest temperature increase occurs near a boundary between tissues of dissimilar thermal conductivities. Therefore, the use of the method is not suggested in applications where the volumes of interest is very small and in contact with the air, such as small extremities of small animals. On the contrary, the speed of the method and its accuracy when used with human body tissues may suggest its use as part of a real-time MRI scan protocol.

While there are some minor differences between the results produced with the fast spatial filter approximation and those from the full FD approach, it is clear that the results provide information much more directly relevant to safety and tissue damage than does SAR_{10 g} [12]. Because the proposed method also requires less time than is required to calculate the SAR_{10 g} throughout the sample, it is hoped that the obstacles to calculating temperature distribution for evaluation of safety will seem significantly reduced so that temperature will be calculated more often.

V. Conclusion

We have presented a new method for fast calculation of temperature in tissue samples by replacing the term for thermal conduction with a spatial filter. The approach produces results in good general agreement with full FD calculations of temperature, but requires much less computation time.

Biographies

Giuseppe Carluccio (M’11) received the Laurea degree (summa) and the Laurea Specialistica degree (summa cum laude) both in electronics engineering from the Politecnico di Milano, Milan, Italy, in 2005 and 2010, respectively, and the M.Sc. and Ph.D. degrees in electrical and computer engineering from the University of Illinois at Chicago (UIC), Chicago, USA, in 2011.

His research interests include applied electromagnetic, specifically waves propagation in biological tissues, RF shimming in magnetic resonance imaging, safety in magnetic resonance imaging, and temperature increase in biological tissues. He is currently a Postdoctoral Fellow in the Department of Radiology, New York University, New York, USA.

Dr. Carluccio received the 2011 Provost and Deiss Award at the UIC.

Danilo Erricolo (S′97–M′99–SM′03) received the Laurea degree (summa cum laude) in electronics engineering from the Politecnico di Milano, Milano, Italy, in 1993, and the Ph.D. degree in electrical engineering and computer science from the University of Illinois at Chicago (UIC), Chicago, USA, in 1998.

He is a currently a Professor with the Department of Electrical and Computer Engineering, UIC, where he is also the Director of the Andrew Electromagnetics Laboratory. He has authored or coauthored more than 170 publications in refereed journals and international conferences. In 2009, he was a U.S. Air Force Summer Faculty Fellow. His primary research interests include electromagnetic scattering, magnetic resonance imaging, radar, wireless communications, and electromagnetic compatibility. His research activity has been supported by the Department of Defense and the National Science Foundation.

Dr. Erricolo is a member of Eta Kappa Nu and was elected a full member of Commissions B, C, and E of the U.S. National Committee of the International Union of Radio Science (USNC-URSI), a committee of the National Academies. He served for USNC-URSI Commission E as Secretary (2004–2005), Vice-Chair (2006–2008), and Chair (2009–2011); since 2009, he has been serving as the Chair of the USNC-URSI Ernest K. Smith Student Paper Competition, and he was an elected Member at Large of USNC-URSI for the triennium 2012–2014. He is an Associate Editor for the IEEE ANTENNAS AND WIRELESS PROPAGATION LETTERS. He was the Vice-Chair of the Local Organizing Committee of the XXIX URSI General Assembly (Chicago, IL, USA, August 7–16, 2008) and the General Chair of the 2012 IEEE Antennas and Propagation International Symposium/USNC National Radio Science Meeting (Chicago, IL, USA, July 8–14, 2012). He was elected as a member of the Administrative Committee of the IEEE Antennas and Propagation Society for the triennium 2012–2014.

Sukhoon Oh received the B.S. degree from KonKuk University, Seoul, Korea, in 1998, and the Ph.D. degree from Kyung Hee University, Seoul, in 2006, both in biomedical engineering. During his doctoral study, his research was focused mainly on magnetic resonance electric impedance tomography, working to show a cross-sectional image of electric conductivity and permittivity for tumor detection in the human body.

He has been a Research Associate at the Center for NMR Research (CNMRR), Pennsylvania State University, University Park, USA, since 2008 after his postdoctoral training (2006–2008) at the CNMRR, where he extended his research area to the electromagnetic (EM) field simulations of RF coils, including transmit array coils. Recently, he has been involved in developing and/or performing temperature and specific energy absorption rate (SAR) mapping of various MR safety related issues by using both MR imaging EM field simulations. He is currently a Research Assistant at the Center for Biomedical Imaging, New York University Langone Medical Center (NYU), New York, USA. At NYU, he continues his research about the effect of high-dielectric materials on the image signal-to-noise ratio and SAR in a high field-strength (7T) MRI system.

Christopher M. Collins (M’00–SM’12) received the Baccalaureate degree in engineering science from The Pennsylvania State University (PSU), University Park, USA, in 1993, and the Ph.D. degree in bioengineering from The University of Pennsylvania, Philadelphia, USA, in 1999.

He joined the faculty in Radiology at PSU in 2001 after a postdoctoral fellowship there, becoming a Full Professor in 2010. He is currently a Professor of Radiology at the New York University Langone Medical Center, New York, USA, as a member of the Bernard and Irene Schwatz Center for Biomedical Imaging. His research interests include use of numerical methods considering field/tissue interactions to simulate, evaluate, and ensure safety and efficacy of MRI.