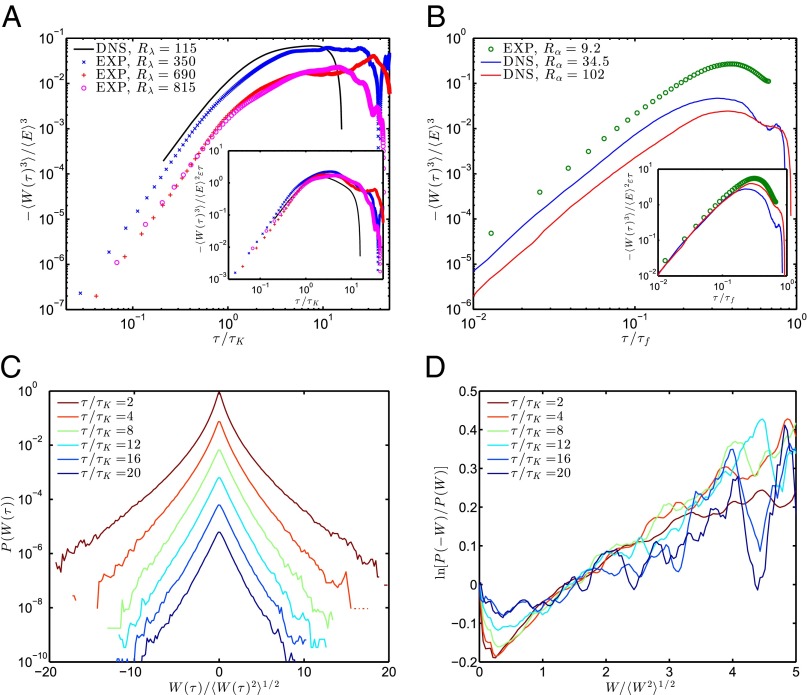
Fig. 2.

(A) The third moment of energy increments $W\left(\tau \right)=E\left(t+\tau \right)-E\left(t\right)$ as a function of τ in 3D turbulence for different Reynolds numbers from both experiments (EXP) and direct numerical simulations (DNS). The quantity $-\langle W{\left(\tau \right)}^3\rangle$ grows like ${\tau }^3$ at short times. The curves obtained at different Reynolds numbers collapse once scaled using [3] (Inset). (B) The third moment of $W\left(\tau \right)$ from 2D turbulence experiments. Features similar to 3D turbulence are observed, i.e., $\langle W^3\left(\tau \right)\rangle$ is negative and nearly saturates when $\tau /{\tau }_f\sim 1$, where ${\tau }_f\sim {\left(l_F^2/\epsilon \right)}^{1/3}$ is the characteristic time corresponding to scale $l_F$ (SI Text). (C) PDFs of $W\left(\tau \right)$ at different values of τ, in the ${\tau }_K\le \tau \le T$ range, corresponding to 3D experimental flow at $R_{\lambda }=350$. The values of $W\left(\tau \right)$ are normalized by their rms values. For clarity, the PDFs have been shifted by a factor of 10 from each other. The PDF tails can be plausibly represented by exponentials. (D) The logarithm of the ratios of the probability of $-W$ and W as a function of W $\left(W>0\right)$ at different values of τ. The linear prediction of [1], which has been shown to apply in many systems in presence of several thermostats, does not simply apply for turbulence.