Nonlinear flight dynamics and stability of hovering model insects

Abstract

Current analyses on insect dynamic flight stability are based on linear theory and limited to small disturbance motions. However, insects' aerial environment is filled with swirling eddies and wind gusts, and large disturbances are common. Here, we numerically solve the equations of motion coupled with the Navier–Stokes equations to simulate the large disturbance motions and analyse the nonlinear flight dynamics of hovering model insects. We consider two representative model insects, a model hawkmoth (large size, low wingbeat frequency) and a model dronefly (small size, high wingbeat frequency). For small and large initial disturbances, the disturbance motion grows with time, and the insects tumble and never return to the equilibrium state; the hovering flight is inherently (passively) unstable. The instability is caused by a pitch moment produced by forward/backward motion and/or a roll moment produced by side motion of the insect.

1. Introduction

Insect flight dynamics and dynamic flight stability are of great interest to researchers who study the biomechanics of insect flight and to engineers who try to make insect-like micro aerial vehicles.

In recent years, much work has been carried out in this area [1–9], using an averaged model and the linear theory borrowed directly from the literature of aircraft flight dynamics. In the averaged model, it is assumed that the wings beat fast, so that the rigid-body modes of the central body are not excited, and the insect can be treated as a rigid body of 6 degrees of freedom (the effects of the flapping wings on the body being represented by the wingbeat-cycle-average forces and moments that can vary with time over the timescale of the central body). With the averaged model, the standard aircraft equations of motion [10] can be used for flying insects. Recent numerical [11,12] and theoretical [3,13] studies have shown that the averaged model works very well for insects who have relatively high wingbeat frequency and small wing-mass to body-mass ratio (hence very small amplitude of body oscillation); for insects who have relatively low wingbeat frequency and large wing-mass to body-mass ratio (hence relatively large amplitude of body oscillation), the averaged model works less well, nevertheless, it can still correctly predict the trend of variation of the dynamic properties. The linear theory assumes that the animal's motion consists of small disturbances from the equilibrium flight; thus, the equations of motion are linearized about the equilibrium point, and the aerodynamic forces and moments are represented as analytical functions of the motion variables (state variables) and the aerodynamic derivatives [10]. The resulting system of linear ordinary differential equations can be solved by the techniques of eigenvalue and eigenvector analysis [10].

Using this framework, Taylor & Thomas [1] studied forward flight dynamic stability in desert locusts, providing the first formal quantitative analysis of dynamic stability in a flying animal. They obtained the aerodynamic derivatives by measuring the aerodynamic forces and moments of tethered locusts in wind tunnel at various wind speeds and body attitudes. Sun & Xiong [2] studied the flight stability of a bumble-bee at hovering. They obtained the aerodynamic derivatives using the method of computational fluid dynamics (CFD; the computational approach allows simulation of the inherent stability of a flapping motion in the absence of active control, which is difficult to achieve in experiments using real insects). Sun et al. [3,4] further studied the hovering stability in several insects with various sizes and wingbeat frequencies (hoverfly, dronefly, cranefly and hawkmoth). Faruque & Humbert [5,6] and Cheng & Deng [7] studied the stability in several hovering model insects (fruitfly, stalk-eyed fly, bumble-bee and hawkmoth). They estimated the aerodynamic derivatives using the blade-element theory and the slopes of experimental lift and drag curves of a sweeping model fruitfly wing. Schenato et al. [8] and Deng et al. [9] developed stabilization control algorithms for flapping flight of robotic insects.

Because of the linearization, the above-mentioned analyses are limited to small disturbance motions. The aerial environment of flying insects is filled with swirling eddies, sharp velocity gradients and wind gusts, and large disturbances are common [14]. Therefore, it is important to study the nonlinear flight dynamics and stability of insects in large disturbance motions. Taylor & Zbikowski [15] made an attempt to take the nonlinearities into account. They used the nonlinear equations of motion; however, the aerodynamic forces and moments were represented by linearized time-periodical functions based on measurements from tethered locusts. Liu et al. [16] made a similar attempt; they also used the nonlinear equations of motion with the aerodynamic force and moment terms represented by linearized time-periodical functions (their aerodynamic forces and moments were computed by a CFD method). Because aerodynamic forces and moments are linearized, these studies [15,16] are also limited to small disturbance motions. One way to study the nonlinear, large disturbance motions is to solve the complete equations of motion and flow equations.

In this study, we numerically solve the complete equations of motion coupled with the Navier–Stokes equations to simulate the large disturbance motions and analyse the nonlinear flight dynamics and stability of hovering model insects. We consider two representative model insects: a model hawkmoth and a model dronefly. The former may represent insects with relatively large size and low wingbeat frequency (mass, 1578.6 mg; frequency, 26 Hz); the latter may represent insects with relatively small size and high wingbeat frequency (mass, 88.9 mg; frequency, 164 Hz). First, we obtain the solution of the equilibrium flight; then, we give various disturbances to the equilibrium solution and study the stability of the equilibrium flight.

2. Material and methods

2.1. Governing equations and the solution method

2.1.1. Equations of motion

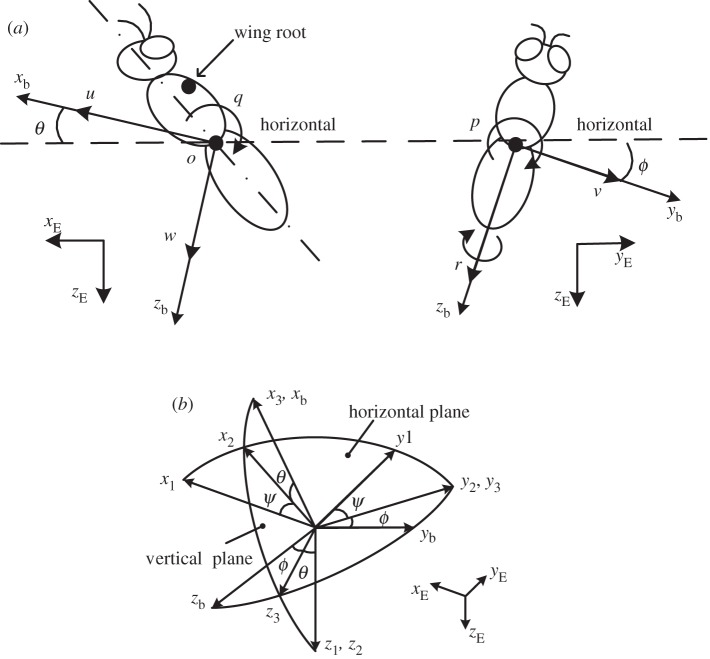
Let frame (x_E, y_E, z_E) be an earth-fixed, inertial frame; the x_E and y_E axes are horizontal and, the z_E axis is vertical, pointing downward (figure 1a). Let (x_b, y_b, z_b) be a frame fixed on the insect body with its origin at the centre of mass of the wingless body; x_b and z_b are in the longitudinal symmetrical plane of the body and y_b points to the right side of the insect (figure 1a). The orientation of the insect's body or the (x_b, y_b, z_b) frame is given by the three Euler angles [10] of the body, denoted by ψ, θ, ϕ (figure 1b); in this study, they are called as yaw, pitch and roll angles, respectively. The equations of motion of a flying insect are (see the electronic supplemental material for the derivation of the equations):

2.1a

2.1b

2.1c

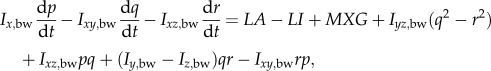2.1d

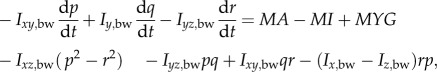2.1e

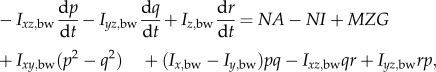2.1f

2.1g

and

2.1h

where u, v and w denote the x_b, y_b and z_b components of the velocity of the insect body, respectively, and p, q and r denote the x_b, y_b and z_b components of the angular velocity of the body, respectively; m is the total mass of the insect (body mass plus wing mass); I_x,bw, I_y,bw, I_z,bw, I_xy,bw, I_yz,bw and I_zx,bw are the moments and products of inertial of the body and wings; XA, YA and ZA denote the x_b, y_b and z_b components of the total aerodynamic force, respectively, and LA, MA and NA denote the x_b, y_b and z_b components of the total aerodynamic moment about the centre of mass of the body, respectively; XI, YI and ZI denote the x_b, y_b and z_b components of the inertial force owing to the flapping wings, respectively, and LI, MI and NI denote the x_b, y_b and z_b components of the moment produced by the inertial forces of the flapping wings, respectively; MXG, MYG and MZG denote the x_b, y_b and z_b components of the moment about the centre of mass of the body produced by the weight of the wings.

Figure 1.

(a) Definition of the state variables and sketches of the reference frames. (b) The orientation of the insect is given by a series of three consecutive rotations, the Euler angles [10].

u, v, w, p, q, r, θ and ϕ, which determine the motion of the flying system, are called state variables (the yaw angle ψ is not independent and is determined by q, r, θ and ϕ; see the electronic supplementary material).

2.1.2. The Navier–Stokes equations

The Navier–Stokes equations, which determine the aerodynamic forces and moments in equation (2.1), are

2.2a

and

2.2b

where u is the fluid velocity, p is the pressure, ρ is the density, v is the kinematical viscosity, 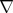is the gradient operator and 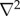is the Laplacian operator.

Equation (2.2) is numerically solved over moving overset grids, because there is relative motion between the left and right wings. The solution method is the same as that used by Sun et al. in several previous studies [17–19] and, a description of it is given in the electronic supplementary material (the computational grids and grid resolution tests are also given there).

2.1.3. Integration method of coupling equations of motion with the Navier–Stokes equations

The equations of motion (equation (2.1)) and the Navier–Stokes equations (equation (2.2)) must be coupled in the solution process, because the aerodynamic forces and moments in the equations of motion must be obtained from the solution of the Navier–Stokes equations, and the boundary condition of Navier–Stokes equations must be obtained from the insect's motion governed by the equations of motion. The integration process is as follows. Suppose that at time t_n the motion of the insect body (u, v w, p, q, r, ψ, θ and ϕ) are known (the wing motion with respect to the body is prescribed); hence, the boundary conditions of the Navier–Stokes equations are known, and also suppose that the flow before t_n is known. Then, the Navier–Stokes equations are solved to provide the aerodynamic forces and moments at t_n. Next, equation (2.1) is marched to the next time station t_{n + 1}, using the Euler predictor–corrector method (which has second-order time accuracy). The process is repeated in the next step, and so on (see the electronic supplementary material for a more detailed description of the integration method).

2.2. Wings, flapping motion and flight data

The platforms of the model wings of the dronefly and the hawkmoth were obtained from the measured data of Liu & Sun [20] and Ellington [21], respectively, and the wing section was a flat plate of 3 per cent thickness with rounded leading and trailing edges. The model wings were assumed to be rigid.

On the basis of experimental data [20,22–24], the flapping motion of a wing was assumed as follows. The motion consisted of two parts: the translation (azimuthal rotation) and the rotation (flip rotation; the out-of-plane motion of the wing (deviation) is neglected). The time variation of the positional angle (ϕ) of the wing was approximated by the simple harmonic function:

2.3

where n is the wingbeat frequency, 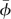is the mean stroke angle and Φ is the stroke amplitude. The angle of attack of the wing (α) took a constant value during the down- or upstroke translation (the constant value was denoted by α_d for the downstroke translation and α_u for the upstroke translation); around stroke reversal, the wing flipped, and α changed with time according to the simple harmonic function. The function representing the time variation of α during the supination at mth cycle was

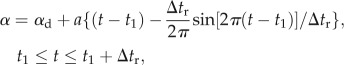2.4

where Δt_r is the time duration of wing rotation during the stroke reversal, and a is a constant:

2.5a

where t₁ is the time when the wing-rotation started:

2.5b

where T is the wingbeat cycle. The expression of the pronation could be written in the same way. From equations (2.3)–(2.5), we see that to prescribe the flapping motion, Φ, n, Δt_r, α_d, α_u and 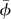must be given.

Morphological and wing motion parameters for the dronefly were taken from the data by Liu & Sun [20] and those for the hawkmoth from the data by Willmott & Ellington [23,24]. It should be noted that moments and products of inertia of wing and roll and yaw moments and products of inertia of body were not given in these references. Moments and products of inertia of wing were estimated using the data on density distribution of a dronefly wing [25]. Roll and yaw moments and products of inertia of body were estimated using pictures showing the lateral and dorsal–ventral views of the wingless body [4], assuming constant density.

Morphological data for the bodies are listed in table 1, and those for the wings are listed in table 2. Wing and body kinematical data are listed in table 3. From table 3, we see that all needed wing-kinematical parameters are given, except α_d, α_u and 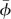. These three parameters are determined in the process of obtaining the periodical solution of hovering. The reasons for not using experimental data for the three parameters are as follows. There are necessarily small errors in the measurement. When there are small errors in the wing kinematical parameters, a periodic solution not representing a hover flight, but a flight with some small speed is obtained [25]; for example, if the measured angle of attack is a little larger than the real one, then the computed periodic solution gives an upward flight of small speed. To overcome this problem, we do not use experimental data to prescribe α_d, α_u and 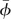, but determine them in the solution process, by requiring that they take values such that hovering flight is ensured. The reason for only three parameters being determined in this way is that there are three conditions to be met in hovering flight: zero mean horizontal velocity, zero mean vertical velocity and zero mean pitch rate. The reason for choosing α_d, α_u and 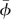to be determined in the solution process is that experimental data for α_d and α_u have relatively large error [20] and aerodynamic forces, and moments are very sensitive to the variations in α_d, α_u and .

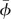Table 1.

Morphological data of body (DF, model dronefly; HM, model hawkmoth). m_bd, mass of body; I_x,b, I_y,b, I_z,b, I_xy,b and I_yz,b, moments and products of inertia of body; l_b, body length; l₁, distance between the wing-base axis and the centre of mass of the body; χ₀, free body angle (with χ₀ and l₁ known, the relative position of the wing-base axis and the centre of mass of the body can be determined).

ID	mbd (mg)	lb (mg)	l1/lb	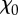(°)	Ix,b (kg m2)	Iy,b (kg m2)	Iz,b (kg m2)	Ixz,b (kg m2)
HM	1485	42.49	0.26	82.9	1.01 × 10−7	1.42 × 10−7	5.24 × 10−8	−5.96 × 10−8
DF	87.76	14.11	0.13	52	5.60 × 10−10	1.18 × 10−9	7.17 × 10−10	−5.00 × 10−10

Table 2.

Morphological data of wing (DF, model dronefly; HM, model hawkmoth). m_wg, mass of one wing; R, wing length; c, mean chord length of wing; S, area of one wing; r₂, radius of second moment of wing area; I_x,w, I_y,w and I_z,w, moments of inertia of wing about x_w, y_w and z_w axes, respectively; I_xy,w, product of inertia of wing.

ID	mwg (mg)	R (mm)	c (mm)	S (mm2)	r2/R	Ix,w (kg m2)	Iy,w (kg m2)	Iz,w (kg m2)	Ixz,w (kg m2)
HM	46.82	48.5	18.37	890.9	0.51	1.59 × 10−9	1.94 × 10−8	1.78 × 10−8	3.86 × 10−10
DF	0.56	11.2	2.98	33.34	0.55	5.23 × 10−13	1.25 × 10−11	1.20 × 10−11	8.04 × 10−13

Table 3.

Kinematic data of wing and body (DF, model dronefly; HM, model hawkmoth). Φ, n, Δt_r, stroke plane angle β, mean body angle χ, Reynolds number of wing Re (Re = cU/ν, where ν is the kinematical viscosity of the air and U the mean flapping velocity, U = 2Φnr₂).

ID	Φ (°)	n (Hz)	Δtr (T)	β (°)	χ (°)	Re
HM	114.4	26.1	0.3	0	54.8	3315
DF	107.1	164	0.3	0	42	782

2.3. The equilibrium flight

To study the stability of hover flight, we need to first obtain the solution to equations (2.1) and (2.2) that represents the equilibrium flight. Because of the periodically varying aerodynamic and inertial forces of the flapping wings, a hovering or constant-speed flying insect is a cyclically forcing system, and generally, the flight is in a cyclic-motion equilibrium. The equilibrium flight, here hovering, is represented by a periodical solution of equations (2.1) and (2.2). A method of obtaining the periodic solution of hover flight has been developed by Wu et al. [25]. A brief description of the method and the solution process is given in the electronic supplementary material.

2.4. Solution of the disturbance motion and flight stability

With the periodic solution of the equilibrium flight known, its stability is investigated by giving the equilibrium solution a perturbation at initial time and then marching equation (2.1) and (2.2) in time.

Let the periodic solution be given between t = −T and t = 0 (where T is the wingbeat period or the period of the periodic solution). If we simply add initial disturbances to the periodical solution at t = 0, then there would be an abrupt change in flow field, which could make the flow solution difficult to converge. We avoid this problem by adding the initial disturbances in a finite but short time interval: from t = −0.1T to t = 0; in this short interval, initial disturbances quickly but smoothly change from zero to the desired values. Then, we continue to solve equation (2.1) and (2.2) to see whether the disturbance motion will die out or not.

As defined earlier, u, v and w are the x_b, y_b and z_b components of the velocity of the body centre of mass, respectively. In hover flight, the x_b axis is approximately horizontal and z_b axis approximately vertical, and u and w can approximate the horizontal and vertical velocities, respectively, of the insect. In disturbance motions, the body, hence the x_b, y_b and z_b axes, may rotate by large angles, and u and w can no longer approximate the horizontal and vertical velocities of the insect. In the following, we use u_E and v_E to denote the forward (or backward) and lateral horizontal velocities, respectively, and w_E to denote the vertical velocity (they are the x_E, y_E and z_E components of the velocity of the body centre of mass, respectively). u_E, v_E and w_E are related to u, v and w as follows:

2.6a

2.6b

and

2.6c

3. Results

When presenting the results, non-dimensional quantities are used. In the non-dimensionalization, U, c and c/U are taken as reference velocity, length and time, respectively (here, U is the mean flapping velocity, defined as 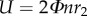and c is the mean chord length of wing).

First, the equations of motion coupled with the Navier–Stokes equations were solved to obtain the periodic solutions that represent the hovering flight. The solutions for the two model insects are given in the electronic supplementary material.

Then, various initial disturbances were added to the periodic solution and equations (2.1) and (2.2) were solved to obtain the disturbance motions. Eight types of initial conditions were considered: (i) a horizontal velocity in x_E direction, which simulated a horizontal gust in −x_E direction or a head-on gust; (ii) a horizontal velocity in y_E direction, which simulated a lateral gust from the right; (iii) a horizontal velocity in the direction 45° from the x_E axis (or horizontal velocities in both x_E and y_E axes), which simulated a oblique gust; (iv) a vertical velocity in z_E direction, which simulated a gust in −z_E direction or an upward gust; (v) a vertical velocity in −z_E direction, which simulated a gust in z_E direction or a downward gust; (vi) an initial rotation about the y_b-axis or an initial pitch; (vii) an initial rotation about the x_b-axis or an initial roll; and (viii) an initial rotation about a line 45° from the x_b-axis (rotations about both the x_b- and y_b-axes). For each of the types of initial conditions, initial disturbance with various magnitudes (two to five magnitudes) was considered.

The disturbance motions are described by u_E, v_E and w_E (velocity of the centre of mass) and ψ, θ and ϕ (body attitude) of insects. For the model hawkmoth, results of the eight types of initial conditions are shown in figures 2–4. For the model dronefly, only the results of four types of initial conditions are given here (figure 5).

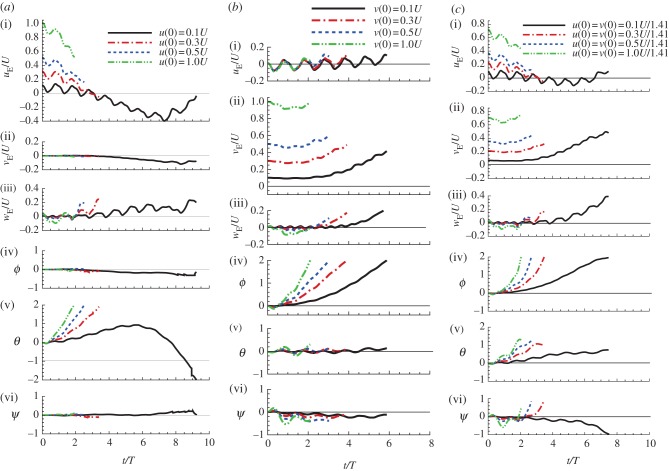
Figure 2.

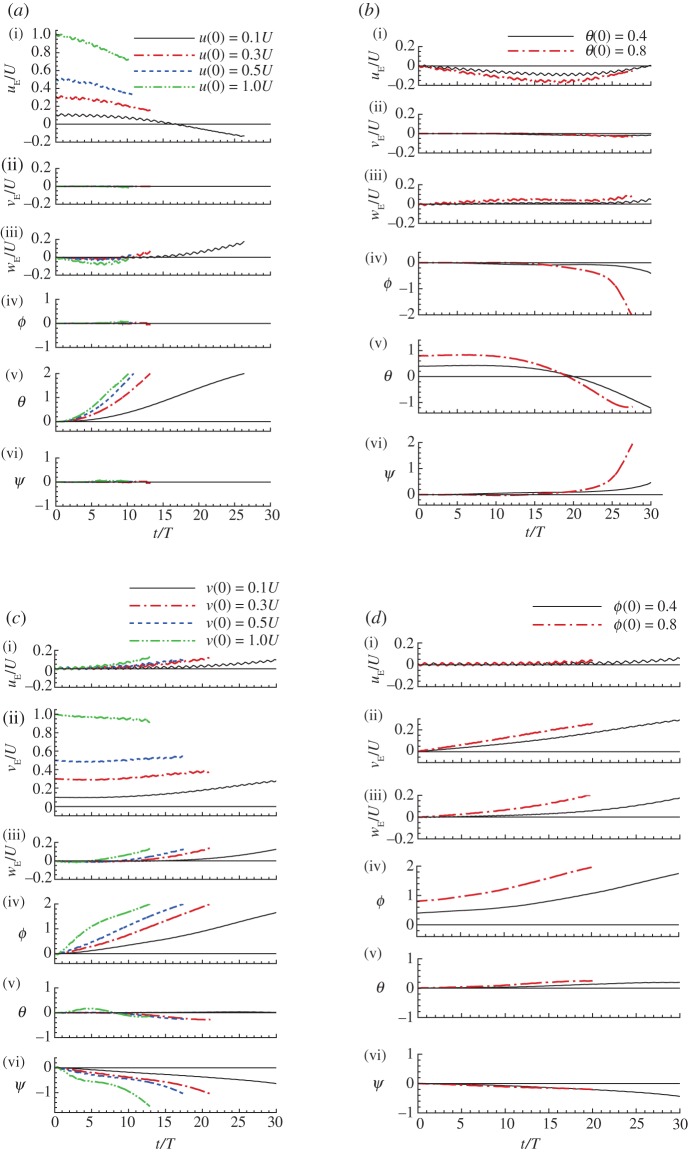
Disturbance motions of the model hawkmoth after horizontal gusts. (a) After a horizontal gust in the −x_E direction (head-on gust): u(0)/U = 0.1, 0.3, 0.5 and 1 (other variables at t = 0 are zero). (b) After a horizontal gust in the −y_E direction (lateral gust from the right): v(0)/U = 0.1, 0.3, 0.5 and 1 (other variables at t = 0 are zero). (c) After a horizontal gust in the direction 45° from the x_E-axis: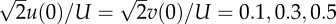 and 1 (other variables at t = 0 are zero). (Online version in colour.)

Figure 3.

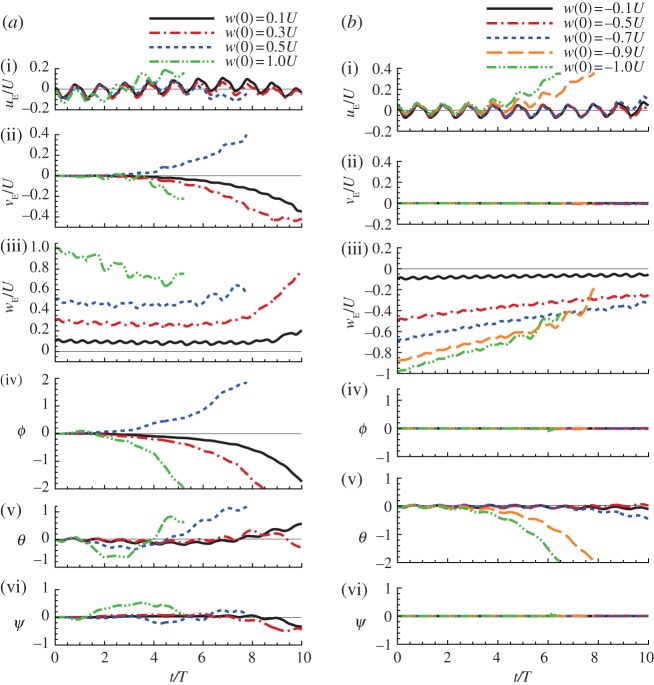
Disturbance motions of the model hawkmoth after vertical gust. (a) After a vertical gust in the −z_E direction (upward gust): w(0)/U = 0.1, 0.3, 0.5 and 1 (other variables at t = 0 are zero). (b) After a vertical gust in the z_E direction (downward gust): w(0)/U = −0.1, −0.5, −0.7, −0.9 and −1 (other variables at t = 0 are zero). (Online version in colour.)

Figure 4.

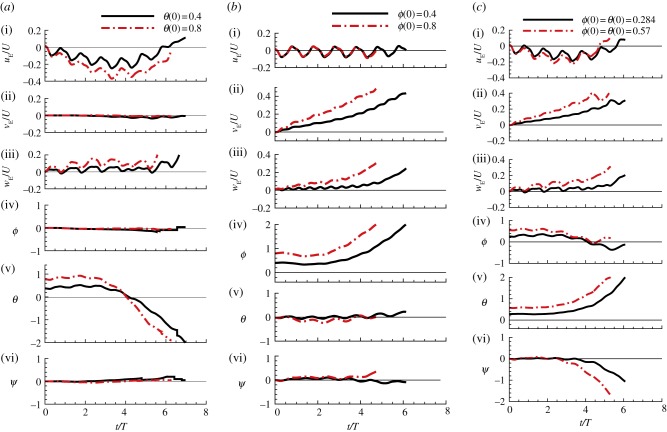
Disturbance motions of the model hawkmoth after initial rotation. (a) After an initial rotation about the y_E-axis (an initial pitch): θ(0) = 0.4 and 0.8 (other variables at t = 0 are zero). (b) After an initial rotation about the x_E-axis (an initial roll): ϕ(0) = 0.4 and 0.8 (other variables at t = 0 are zero). (c) After an initial rotation about a line 45° from the x_E-axis, ϕ(0) = θ(0) = 0.284 and 0.57 (other variables at t = 0 are zero). (Online version in colour.)

Figure 5.

Disturbance motions of the model dronefly. (a) After a head-on gust: u(0)/U = 0.1, 0.3, 0.5 and 1 (other variables at t = 0 are zero). (b) After an initial pitch: θ(0) = 0.4 and 0.8 (other variables at t = 0 are zero). (c) After a lateral gust: v(0)/U = 0.1, 0.3, 0.5 and 1 (other variables at t = 0 are zero); (d) after an initial roll: ϕ(0) = 0.4 and 0.8 (other variables at t = 0 are zero). (Online version in colour.)

4. Discussion

4.1. Hovering flight is inherently (passively) unstable

As an example, we examine the result of the model hawkmoth in figures 2–4.

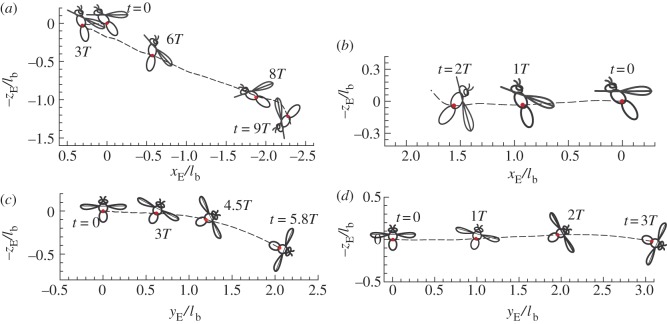
When the initial disturbance is a head-on gust (figure 2a), for relatively small initial disturbance (u(0)/U = 0.1; see the black lines in figure 2a), there are oscillations in u_E and θ, i.e. the insect moves forward and backward while pitching up and down, and after approximately one oscillation, the insect tumbles and never returns to the equilibrium state, which is illustrated in figure 6a. For relatively large initial disturbance (e.g. u(0)/U = 0.5; see the blue dotted lines in figure 2a), the insect moves forward while pitching up, and tumbles after a short time, which is illustrated in figure 6b. When the initial disturbance is a pitch angle (figure 4a), for small and large initial disturbances (θ(0) = 0.4 (23°) and 0.8 (46°)), there are oscillations in θ and u_E, i.e. the insect pitches up and down while moving backward and forward, and after less than one oscillation, the insect tumbles. We call the above-mentioned instabilities ‘pitch instability’. For the cases of small longitudinal initial disturbances (u(0)/U = 0.1 in figure 2a; θ(0) = 0.4 in figure 4a), the disturbance motions are similar to those predicted by linear theory in previous studies [2,5,7].

Figure 6.

Spatial location of centre of mass and body orientation of the hawkmoth in disturbance motion. (a) After a head-on gust, u(0)/U = 0.1; (b) after a head-on gust, u(0)/U = 0.5. (c) After a lateral gust, v(0)/U = 0.1; (d) after a lateral gust, v(0)/U = 0.5. (Online version in colour.)

When the initial disturbance is a lateral velocity to the right (figure 2b), for small and large initial disturbances (v(0)/U = 0.1–1), the insect moves to the right while rolling to the same direction, and tumbles in about 5.5 wingbeat cycles for v(0)/U = 0.1 and in about three wingbeat cycles for v(0)/U = 0.5; this is illustrated in figure 6c,d. When the initial disturbance is a roll angle (figure 4b), for small and large initial disturbances (ϕ(0) = 0.4 and 0.8), the insect rolls to the right while moving to the same direction, and tumbles in about 5.5 wingbeat cycles for ϕ(0) = 0.4 and in about four wingbeat cycles for ϕ(0) = 0.8. We call the above-mentioned instabilities ‘roll instability’. For the cases of small lateral initial disturbances (v(0)/U = 0.1 in figure 2b; ϕ(0) = 0.4 in figure 4b), again, the disturbance motions are similar to those predicted by linear theory in previous studies [4,26].

When the initial disturbance is a oblique gust (figure 2c), the longitudinal motion is similar to that of the case of a head-on gust (comparing u_E, w_E and θ in figure 2c with those in figure 2a), and the lateral motion is similar to that of the case of lateral gust (comparing v_E, ϕ and ψ in figure 2c with those in figure 2b). The motion has both ‘pitch instability’ and ‘roll instability’, but the stabilities grow a little slower than those in the cases of head-on gust and lateral gust (e.g. ϕ in figure 2c grows to 2 at t/T = 7.5, but ϕ in figure 2b grows to 2 at t/T = 6). When the initial disturbance has pitch and roll rotations (figure 4c), u_E and θ are similar to those of the case in which the initial disturbance is a pitch rotation (comparing u_E and θ in figure 4c with those in figure 4a), and v_E and ϕ are similar to those of the case in which the initial disturbance is a roll rotation (comparing v_E and ϕ in figure 4c with those in figure 4b). Again, the motion has both ‘pitch instability’ and ‘roll instability’.

When the initial condition is an upward gust, or the insect has an initial downward velocity, w_E(0) > 0 (figure 3a), the downward velocity decreases at first (for w_E(0) = 1, w_E decreases with time until t/T = 4.5; for w(0)/U = 0.1, w_E decreases with time until t/T = 8), and the vertical motion seems to be stable. But at later times, θ (and uE) and ϕ (and vE) grows quickly with time, i.e. the ‘pitch instability’ and ‘roll instability’ have developed. When the initial condition is a downward gust, or insect having an initial upward velocity, w(0)/U < 0 (figure 3b), the magnitude of w_E also decreases with time, and the vertical motion seems to be stable, but at longer times, ‘pitch instability’ develops. The larger the initial upward velocity, the earlier the instability develops.

Similar observations can be made from the disturbance motions of the model dronefly (figure 5). We see that for the initial conditions considered, the disturbance motion grows with time and the insect tumbles and never returns to the equilibrium state. We thus conclude that hovering flight of the model insects is inherently (passively) unstable.

4.2. Physical mechanisms of instability

We still take the model hawkmoth (figures 2–4) as an example. Let F₀ denote the wingbeat-cycle-averaged vertical aerodynamics force during hovering (F₀ = mg); let 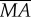and denote the wingbeat-cycle-averaged vertical aerodynamic pitch and roll moments in the disturbance motion; let S denote the area of the wing pair (in figure below, the superscript asterisk denotes a non-dimensional quantity; a force is non-dimensionalized by 0.5ρU²S and a moment by 0.5ρU²Sc).

First, we discuss the ‘pitch instability’ in figure 2a (or in figure 6a,b), i.e. the disturbance motion owing to an initial forward velocity or a head-on gust. In this case, as seen in figure 2a, the disturbance motion mainly has variations in the horizontal velocity (u_E) and pitch angle (θ). In figure 7, we plot u_E and θ, together with the pitch moment (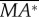) and the horizontal force owing to tilting the weight-supporting vertical force, F₀sin(–θ). At the beginning (t/T = 0−1), the insect moves forward at the initial velocity (figure 7a), and a positive 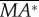(pitch-up moment) is produced (figure 7c). The pitch-up moment makes θ increase (figure 7b), resulting in a negative horizontal force, F₀sin(–θ) (figure 7d). The negative F₀sin(–θ) will decrease the forward-motion velocity. In the cases of large initial forward velocities (u(0) = 0.3, 0.5 and 1), because the pitch moment is very large, θ grows very fast and before the forward-motion velocity decreases to zero, the insect tumbles. In the cases of relatively small initial forward velocities, the pitch moment is not very large, θ grows relatively slowly. For example, for the case of u(0) = 0.1, u_E decreases to zero at t/T ≈ 3 and continues to decreases to a negative value (figure 7a), and a negative 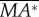(pitch-down moment) is produced (figure 7c). The negative 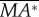would decrease θ; however, because there is a time lag between moment and angular change, θ keeps increasing to a large value (about 50°) and remains positive until t/T ≈ 7.5 (figure 7b). During this period (t/T ≈ 3−7.5), the large and negative F₀^*sin(−θ) accelerates the insect and increases the negative u_E to large magnitudes at t/T ≈ 7.5, which produces a large, negative pitch moment (figure 7c, t/T ≈ 7.5). Now, the situation is similar to the cases of large initial forward velocities discussed earlier: a large pitch moment makes θ grow very fast and the insect tumbles. We thus see that for the case of large initial velocity, the large velocity at the first few wingbeats produces a large pitch moment that causes the insect to tumble. For the case of small initial velocity, pitching motion and forward (or backward) motion enhance each other, driving the forward (or backward) velocity to a large value, and the large velocity produces a large pitch moment that causes the insect to tumble. That is, in both cases, it is the large pitch moment produced by forward (or backward) velocity that causes the insect to tumble, causing the instability. How the forward (or backward) velocity produces pitch moment can be readily explained: when the insect moves forward, in the downstroke, the wings would see a larger relative velocity than that in hovering flight and the drag of a wing is larger than that in hovering flight, whereas in the upstroke, the wings would see a smaller relative velocity than that in hovering flight and the drag is smaller than that in hovering flight. This will result in a wingbeat-cycle mean force in the negative x_b-direction. Because the stroke plane is above the centre of mass, this force will produce a positive pitch moment. Similarly, when the insect moves backward a negative pitch moment will be produced.

Figure 7.

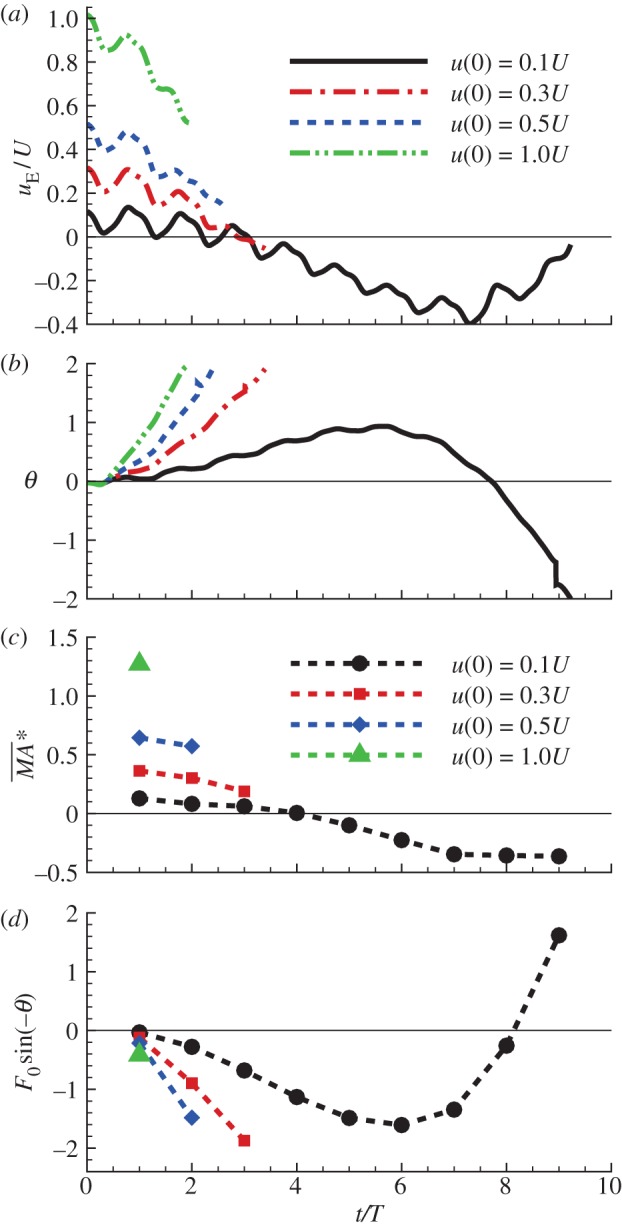
Pitch moment and horizontal force owing to tilting the weight-supporting vertical force of the hawkmoth in the disturbance motion, after a head-on gust: u(0)/U = 0.1, 0.3, 0.5; other variables at t = 0 are zero. (Online version in colour.)

Next, we look at the ‘pitch instability’ in figure 4a, i.e. the disturbance motion owing to an initial pitch angle. Analysis similar to the above has shown that the pitch angle gives a horizontal force, F₀sin(−θ), resulting in backward motion and pitching motion; the horizontal motion and pitching motion enhance each other, driving the backward velocity to a large value; the large velocity produces a large pitch moment that causes the insect to tumble.

Third, we discuss ‘roll instability’ in figure 2b (or in figure 6c,d), i.e. the disturbance motion owing to an initial lateral velocity or a lateral gust. In this case, the disturbance motion mainly has variations in the horizontal velocity (v_E) and roll angle (ϕ; figure 2b). In figure 8a, we plot v_E and ϕ, together with the roll moment 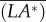and the lateral horizontal force owing to tilting the weight-supporting vertical force, F₀^*sin(ϕ). As seen in figure 8a, the insect moves to the right (v_E(t) > 0) at the initial velocity in the beginning (figure 8a(i), t/T = 0−2) and then v_E(t) increases (figure 8a(ii), t/T = 2−3); a positive roll moment, 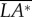, is produced during the side-translational motion (figure 8a(iii), t/T = 0−3); at t/T = 1−2, the insect starts to roll to the right (ϕ > 0) (figure 8a(ii), t/T = 1.5−4). From these data, the development of the instability can be clearly seen (as illustrated in figure 8b): the insect moves to the right and a right-side rolling moment 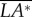(>0) is produced by the side-translational velocity (how the roll moment is produced will be discussed below); the moment 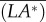rolls the insect to the right (ϕ > 0), tilting the vertical force (F₀ = mg) to the right; the horizontal component of F₀ would enhance the side-translational motion and the roll moment produced by the side-translational motion would enhance the roll, resulting in the instability. Now let us explain how the side-translational velocity could produce a roll moment. When using linear analysis to study the lateral stability of hovering insects, Zhang & Sun [4] and Xu & Sun [26] found that right-side (or left-side) translational velocity will produce a positive (or negative) roll moment, the reasons for which are as follows. When the insect conducts a side-translational motion to the right side, the left wing sees a relative velocity that is approximately directed from wing-root to wing-tip, whereas the right wing sees a relative velocity that is approximately directed from wing-tip to wing-root. Flow velocity from wing-root to wing-tip of the left wing would increase the axial velocity of its leading-edge vortex (LEV) and make the LEV more concentrated than that of the equilibrium flight (hovering flight), whereas flow velocity from wing-tip to wing-root of the right wing would decrease the axial velocity of its LEV and make the LEV more diffused than that of the equilibrium flight. This will result in a larger lift on the left wing and a smaller lift on the right wing, producing the positive roll moment. Similarly, a left-side-translational motion will produce a negative roll moment. In the above-mentioned studies [4,26], only small disturbance motions were considered. But, it is obvious that this mechanism would exist also when side-translational velocity is large. This is confirmed by our data. As an example, figure 9 shows a comparison between the LEVs of the left and right wings at v(0)/U = 0.5. It is seen that the LEV on the right wing is much more diffused than that on the left wing.

Figure 8.

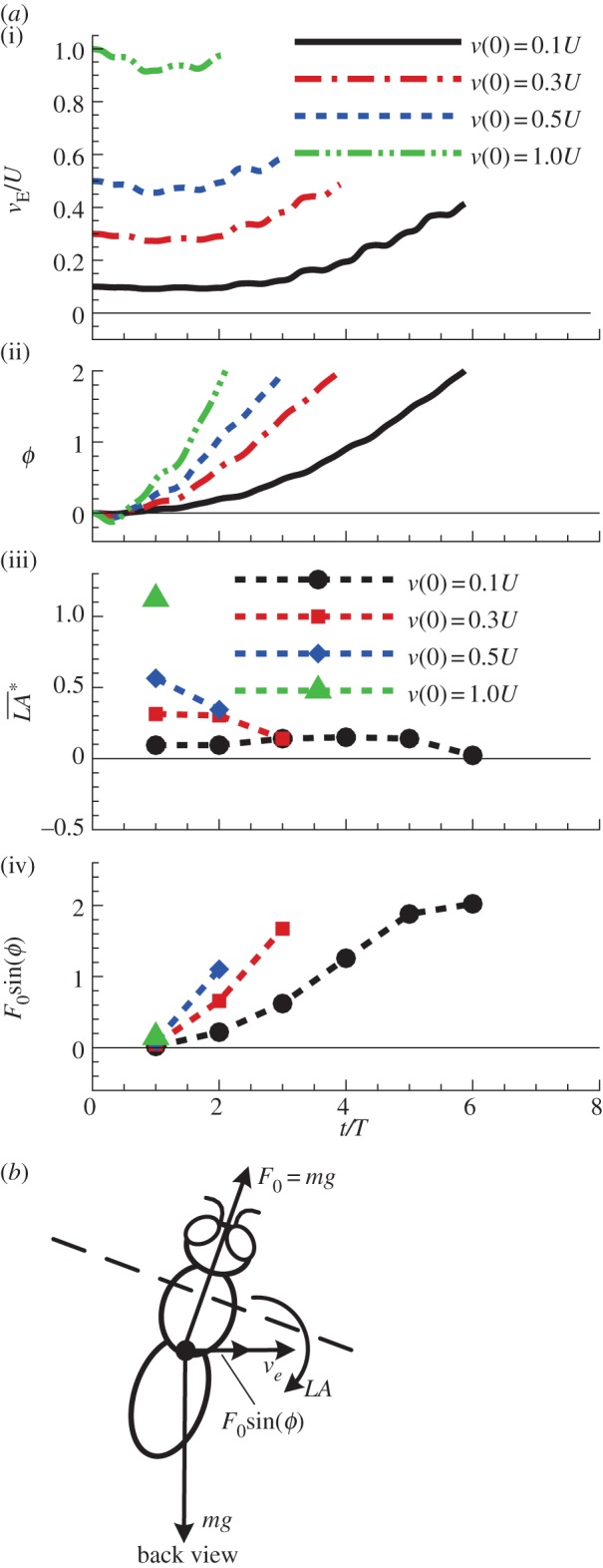
(a) Roll moment and horizontal force owing to tilting the weight-supporting vertical force of the hawkmoth in the disturbance motion, after a lateral gust: v(0)/U = 0.1, 0.3, 0.5; other variables at t = 0 are zero. (b) A sketch illustrating the mutual enhancement of the side-translational motion and the roll motion. (Online version in colour.)

Figure 9.

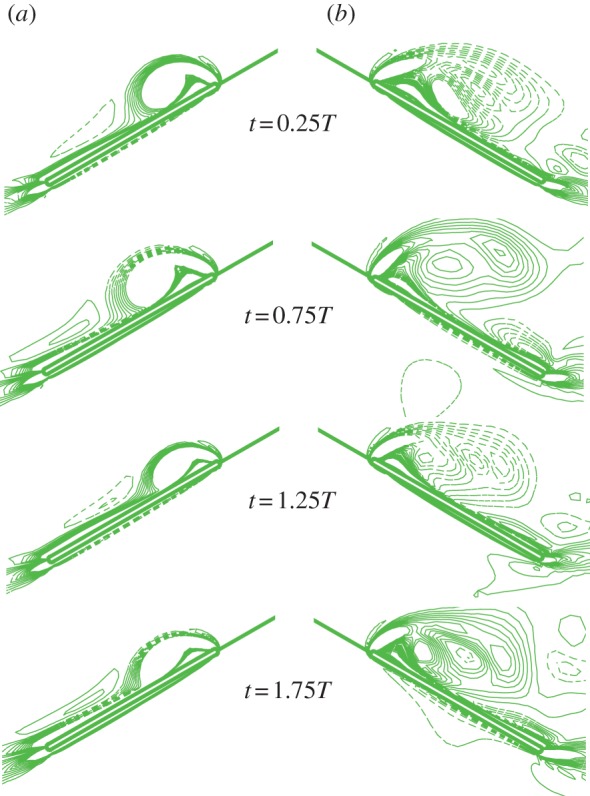
(a) Vorticity plots at 0.7R wing-section at various time for the wings of the hawkmoth in the disturbance motion, after a head-on gust: u(0)/U = 0.5; other variables at t = 0 are zero. (a) Left wing; (b) right wing. Solid and broken lines indicate positive and negative vorticity, respectively. The magnitude of the non-dimensional vorticity (non-dimensioned by c/U) at the outer contour is 2 and the contour interval is 3. (Online version in colour.)

Finally, let us look at the ‘roll instability’ in figure 4b, i.e. the disturbance motion owing to an initial roll angle. Analysis similar to the previous paragraph has shown that the roll angle gives a horizontal force, F₀sin(ϕ), resulting in a right-side horizontal motion and roll motion; the horizontal motion and roll motion enhance each other, resulting in instability. The instabilities in other disturbance motions considered in the previous section are either a ‘pitch instability’ or a ‘roll instability’ and can be similarly explained.

4.3. Comparison with linear theory

When a nonlinear problem is linearized about an equilibrium point, the linearized equation of small perturbation about the equilibrium point can be solved analytically. When the full nonlinear equation is solved numerically for disturbance motions about the equilibrium point, in the case of the perturbation is small, the numerical solution should be approximately the same as the analytical solution. In fact, this can serve as a test of the numerical solution.

Here, we compare the present nonlinear solution with the analytical solution. It is expected that for small disturbance motion, the numerical solution is close to the analytical one. For the hovering hawkmoth and dronefly, the analytical solution of small disturbance motion was obtained by our group [11–13]:

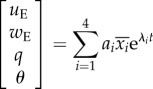4.1a

and

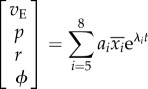4.1b

where λ_i and 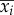(i = 1–4) are the longitudinal eigenvalues and eigenvectors, respectively, and λ_i and 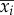(i = 5–8) are the lateral eigenvalues and eigenvectors, respectively; a_i(i = 1–8) is constants. λ_i and 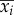(i = 1–8) are given in references [11,12], a_i is determined by given initial conditions.

Electronic supplementary material, figure S6 compares the numerical and analytical results of the model hawkmoth when the initial disturbances are u(0)/U = 0.1 and v(0)/U = 0.1, respectively. The initial disturbances are small. As is expected, in the early time (t/T ≈ 0–2), before the disturbance motion grows large, the numerical solution is close to the analytical solution; however, when the disturbance motion grows large (t/T > 2), discrepancies between the nonlinear and linear solutions become large. Electronic supplementary material, figure S7 shows the corresponding results for the dronefly; the comparison is similar.

5. Conclusions

• — For small and large initial disturbances, the disturbance motion grows with time and the insects tumble and never return to the equilibrium state; hovering flight of the model insects is inherently (passively) unstable.

• — The instability is mainly caused by a large positive (and/or negative) pitch moment produced by the forward (and/or backward) velocity, and/or a large positive (or negative) roll moment produced by the right (or left) side-velocity of the insect.