Abstract
There is an increasing need to develop and apply powerful statistical tests to detect multiple traits-single locus associations, as arising from neuroimaging genetics and other studies. For example, in the Alzheimer's Disease Neuroimaging Initiative (ADNI), in addition to genome-wide single nucleotide polymorphisms (SNPs), thousands of neuroimaging and neuropsychological phenotypes as intermediate phenotypes for Alzheimer's disease, have been collected. Although some classic methods like MANOVA and newly proposed methods may be applied, they have their own limitations. For example, MANOVA cannot be applied to binary and other discrete traits. In addition, the relationships among these methods are not well understood. Importantly, since these tests are not data adaptive, depending on the unknown association patterns among multiple traits and between multiple traits and a locus, these tests may or may not be powerful. In this paper we propose a class of data-adaptive weights and the corresponding weighted tests in the general framework of generalized estimation equations (GEE). A highly adaptive test is proposed to select the most powerful one from this class of the weighted tests so that it can maintain high power across a wide range of situations. Our proposed tests are applicable to various types of traits with or without covariates. Importantly, we also analytically show relationships among some existing and our proposed tests, indicating that many existing tests are special cases of our proposed tests. Extensive simulation studies were conducted to compare and contrast the power properties of various existing and our new methods. Finally, we applied the methods to an ADNI dataset to illustrate the performance of the methods. We conclude with the recommendation for the use of the GEE-based Score test and our proposed adaptive test for their high and complementary performance.
Keywords: aSPU test, GEE, GWAS, Neuroimaging genetics, Score test, Statistical power, Sum of powered score (SPU) test
1 Introduction
Published genome-wide association studies (GWAS) have shown that single nucleotide polymorphisms (SNPs) associated with common diseases and complex traits are not easy to be detected. The main reason is due to their small e ect sizes: the odds ratios from the identified associations are often only 1.1-1.3. It is also realized that using only one single phenotype may not suffice to identify the underlying genetic mechanism, as a complex disease may exhibit its occurrence or progression in several syndromes. Thus, multivariate trait analysis is being increasingly recognized as a potentially useful strategy in genetic studies (Zhu and Zhang 2009). However, a dilemma in joint analysis of multiple traits is the inevitable power loss as more and more non-associated traits are being included; in practice, there is no guarantee that multiple traits being analyzed are all simultaneously associated with the same SNP. Therefore, a key issue in multivariate trait analysis is how to maximally maintain statistical power in the presence of many non-associated traits while gaining the power when many or most of the traits are associated with an SNP.
Various methods have been proposed and applied to multivariate trait analysis. Broadly speaking, any existing method for pedigree or longitudinal data analysis is applicable; see a recent nice review by Yang and Wang (2012). The methods can be classified into a few categories. The first category is to conduct univariate analysis on each trait, then combine their results (Yang et al 2010). For example, for any given SNP, one can conduct a single trait–single SNP analysis for each of the multiple traits, then take the minimum p-value from the univariate analyses with an adjustment for multiple testing. This is like the most commonly adopted approach to single trait–multilocus analysis in GWAS, the so-called UminP approach. The second class is based on dimension reduction on multivariate traits, usually by principal components analysis (PCA) (Lan et al 2003; Wang and Abbott 2007) or by principal components of heritability (PCH) (Klei et al 2008) and related methods (Wang et al 2008; Lin et al 2012). For PCA, a main issue is that a few top PCs may not capture su cient association signals (Aschard et al 2013). For PCH, the sample splitting strategy for population-based studies is not e cient (Yang and Wang 2012), though the modification of Lin et al (2012) overcomes this downside. Nevertheless, the interpretation with the use of a few principal components may not be straightforward, and it is debatable whether there exist a few PCs that can genetically capture a large proportion of trait variations. Importantly, it is not clear how robust these methods are in the presence of many non-associated traits, and how many components are needed. Canonical correlation analysis (CCA) also belongs to this class; it seeks the linear combination of all traits yielding the greatest association with a locus (Ferreira and Purcell 2009). Another special case is simply to take the average (or sum) of multiple traits and then conduct a univariate analysis with this single average (or sum) trait, which is called Average (or Sum) method and has been applied to neuroimaging genetic data recently (Shen et al 2012). As in the case for single trait–multilocus testing, the Average (or Sum) method su ers from severe power loss in the presence of opposite association directions between the traits and a locus (Pan 2009), or even worse, as to be shown later, in the presence of some non-associated traits. The third class includes some classical methods for multivariate data, such as MANOVA (Ferreira and Purcell 2009), which however is not applicable to non-Normal traits, e.g. binary traits. Linear mixed models (LMMs) or generalized least squares for quantitative traits, and generalized linear mixed models (GLMMs) for discrete traits provide a more general alternative (Laird et al., 1982; Fitzmaurize et al., 1993; Li et al 2011; Korte et al., 2012). However, these likelihood-based approaches require one to correctly specify a model, including the correlation structure among the multiple traits, which is often di cult, especially for non-Normal traits. Furthermore, fitting GLMMs is computationally demanding. Alternatively, the generalized estimation equations (GEE) methodology (Liang and Zeger, 1986) is convenient to use, only requiring a correct specification of a marginal mean regression model, not a variance or covariance structure and other higher moments of the traits. In particular, its (generalized) score vector is easy to calculate, in contrast to the intractability in GLMMs. The GEE framework is general and flexible: it can accommodate covariates and various types of traits (Liu et al., 2009; Chen et al., 2011; Lange et al., 2003). Yang and Wang (2012) commented that there may be inflated Type I errors in GEE; we show here that the problem is mainly with the Wald test (Pan 2001) while the Score test and other score-based tests seemed to work well. Hence, in this paper we adopt the GEE framework, applying some existing tests and developing some new ones, to test for association between a single SNP and multiple, possibly a large number of, quantitative traits.
A challenge in association testing with multiple parameters, such as in multilocus analysis or multivariate trait analysis, is the lack of a uniformly most powerful test. Depending on the unknown truth of the underlying association patterns, any given and fixed test may or may not be powerful. For example, depending on how many of a given set of multiple traits are associated with a locus, di erent tests may be more powerful: if only few of the traits are associated, then a univariate minimum p-value (UminP) method based on choosing the most significant p-value of the univariate tests on each of the multiple traits, similar to TATES (van der Sluis et al 2013), would be more powerful; on the other hand, if most or all of the traits are associated with the locus with similar e ect sizes, the simple Average method is expected to be more powerful. Our simulation results will confirm these points later. Accordingly, in multilocus association testing, adaptive tests based on weighting multiple loci di erently have been proposed (e.g. Lin and Tang 2012). However, due to the use of fixed weights, these adaptive tests may still su er from power loss under some situations. Here we propose a class of more highly adaptive tests with a wide range of weights on multiple traits. The goal is that, for a given situation with some unknown association patterns, we can find at least one set of the weights yielding a high-powered test. In our earlier example, if only one trait is associated with a locus, then assigning a large weight to the associated trait while assigning small weights to other traits would be optimal; on the other hand, if all traits are (almost) equally associated with the locus, we would like to assign an equal weight to all the traits. Our proposed class of tests are based on weighting the (generalized) score vector of a marginal generalized linear model (GLM) (McCullagh and Nelder 1983) in GEE; it maintains the computational simplicity of the Score test and the generality and flexibility of GLMs. Each of our proposed test statistics is a sum of powered score statistics, say SPU(γ), in which an integer γ indexes a set of weights on the multiple traits. Our adaptive SPU (aSPU) test essentially estimates and thus chooses the most powerful SPU test for a given dataset.
Another contribution of this work is to point out connections among the existing and new tests. Although some existing methods, such as classic ones like CCA and MANOVA, recently proposed ones like TATES (van der Sluis et al 2013), MultiPhen (O'Reilly et al., 2012) and kernel machine regression (KMR) (Maity et al 2012), and some potentially usable ones like MDMR (McArdle and Anderson 2001), have been suggested for analysis of multivariate traits, their relationships with each other are largely unknown. Here we analytically illuminate on how these existing tests and our proposed tests are related. In particular, when testing on association between multiple quantitative traits and a single SNP in the absence of other covariates, we point out that many existing tests are special cases of the SPU tests. For example, CCA, MANOVA and the GEE-Score test are equivalent, which in turn are closely related to MultiPhen; the Average method coincides with the GEE-SPU(1) test, while TATES is closely related to the GEE-SPU(∞); Under suitable conditions, both MDMR and KMR are the same as the GEE-SPU(2) test. These analytical results will be confirmed in our extensive simulation studies.
Finally we will apply these methods to the NIH Alzheimer's Disease Neuroimaging Initiative (ADNI) data. We aim to detect associations between SNPs and some multivariate neuroimaging phenotypes in several related regions of interest (ROIs). As both imaging and genotyping technologies advance, imaging genetics is emerging as a promising yet challenging field. In particular, due to numerous phenotypes measured for the ROIs, there is a high demand on developing and applying powerful association testing for multivariate traits, given limited multivariate methods available (Glahn et al., 2007). Shen et al. (2010) applied the simple Average method and confirmed two associated genes, APOE and TOMM40. We aimed to investigate how our proposed new tests perform as compared to other existing tests. We will demonstrate the advantages and potential usefulness of the GEE-based tests.
2 Methods
2.1 Generalized Estimating Equations
Suppose that for each subject i = 1, ..., n, we have k traits Yi = (yi1, yi2, ..., yik)′, xi = 0, 1 or 2 is the genotype score (i.e. count of the minor allele) for an SNP of interest, and zi = (zi1, zi2, ..., ziq) is a row vector of q covariates. Define the design matrices for the SNP e ects and covariates as
where 0 is a row vector of all 0's. Xi is a k × k matrix, and Zi is a k × k(q + 1) matrix including the intercept term. Define two regression coe cient vectors as β = (β1, ..., βk)′ for Xi and φ = (φ11, ..., φ1(q+1), ..., φk1, ..., φk(q+1))′ for Zi, where the main interest is on β, the SNP e ects on the traits. The marginal means, E(Yi|xi, Zi) = μi, the SNP and covariates are modeled through a marginal generalized linear model (GLM):
with Hi = (Zi, Xi), = (φ′, β′)′ and g(.) as a suitable link function.
The consistent and asymptotically Normal estimates of β and φ are obtained by solving the GEE (Liang and Zeger, 1986):
where g−1(.) is the inverse function of g(.), ϕ is a possible dispersion parameter, Ai = diag{v(μi1), v(μi2), ..., v(μik)} with v(μim) = Var(yim|xi, zi)/ϕ, and Rw = Rw(α) is a working correlation matrix that may depend on some unknown parameters α. Note that Rw does not have to be correctly specified; for convenience, a working independence model with Rw = I is often used, as done in this paper unless specified otherwise.
With a canonical link function and a working independence model (i.e. Rw = I), it is not di cult to obtain the (generalized) score vector and its consistent covariance estimate:
| (1) |
Where is an estimate of μi, is partitioned according to the score vector components U.1 and U.2 for φ and β respectively.
Binary Traits
For binary traits (coded as 0 and 1), we use the logit link function, and v(μim) = μim(1 − μim). The (m, l)th element of ∂μi/∂ θ′ is Hi,mlμim(1 − μim) with Hi,ml as the (m, l)th element of Hi. We have the score vector and its covariance estimate as
with as an estimate of μi, Ai = diag(μi1(1 − μi1), ..., μim(1 − μim)).
Quantitative traits
We use the identity link g(μim) = μim and v(μim) = ϕ. Then we have
| (2) |
If we assume a common covariance matrix for Yi's across all i, then a better covariance estimate is
which is used by default for its better finite-sample performance (Pan 2001).
2.2 Existing Tests in GEE
Our goal is to detect whether there is any association between any of the traits and the SNP via testing the null hypothesis H0: β = (β1, ..., βk)′ = 0 versus H1: β ≠ = 0.
To construct score-based tests with covariates Zi, we first fit the GEE model under H0, g(μi) = Ziφ, to obtain and . If we denote for subject i, Ui1 as the score vector corresponding to covariates Zi, and Ui2 as the score vector for the SNP, then the score vector under the null hypothesis, with an assumed independent working correlation structure for the traits, is:
The null distribution of the score vector for β is asymptotically Normal under H0:
| (3) |
where V11, V12, V21, V22 are defined in (1).
The Wald test
, where is the estimate of β in the GEE marginal model, and is the sandwich estimate. Under H0, we have asymptotically. In spite of its simplicity and popular use, as well known (Pan 2001) and to be shown later, with a relatively large k, the Wald test in GEE may become too liberal with inflated Type I errors.
The Score test
, where U.2 and Σ.2 are discussed above; it is asymptotically equivalent to the Wald test with the same null distribution . Since we only need to fit the model under the null hypothesis, it is computationally simpler than using the Wald test, which requires fitting a full model. More importantly, as to be shown, the Score test controls the Type I error much better than the Wald test.
The UminP test
, where U.2,j is the jth element of U.2, and .2,jj is the jth entry on the diagonal of .2. Although a numerical integration-based method as for single trait–multilocus testing (e.g. Pan 2009) can be adopted, we use a simulation based method to calculate its p-value. Specifically, we simulate the score vectors U(b) = (U(b),1, U(b),2, ..., U(b),k)′ from its null distribution for b = 1, ..., B, then calculate the null statistics , and the p-value .
With a working independence model Rw = I, each component U.2,j is equal to the score function for the univariate analysis on the jth trait. Hence, the GEE-UminP test is equivalent to the usual UminP test that combines the univariate analyses on the multiple traits.
2.3 New Tests in GEE
For association analysis of rare variants, weighting on the components of the score vector has been recognized as a general and effective approach to synthesizing information contained in the components of the score vector (Lin and Tang 2012). We borrow this idea and apply it to the current context, yielding a weighted score test:
where the weights wj's have to be specified, which is a key and challenging issue. Various choices of the weights have been proposed for analysis of rare variants, all of which are some fixed weights. Our goal is to specify a whole class of weights such that they can cover a wide range of situations: for any given data with unknown true association patterns, we hope that at least one member from the specified class of weights would yield a high-powered test. We reason that, since association information is largely contained in the score vector, the driving force of constructing various score-based tests (as reviewed above), it might be productive to use the score vector to construct the weights. Accordingly, we propose a class of weights for a series of values of γ = 1, 2, ..., ∂, leading to the sum of powered score (U) tests, called SPU tests:
As γ = 1, the SPU(1) test sums up the information in the multiple traits equally, just as the Average (Sum) test. As the power parameter γ increases, the SPU(γ) test puts higher weights on the traits with larger |U.2,j|, while gradually decreasing the weights on the other traits with smaller |U.2,j|. By statistical theory, we know that a trait associated with the SNP is expected to have a larger |U.2,j| while a non-associated one has a smaller value. Hence, an increasing value of γ tends to put higher weights on those more strongly associated traits. An extreme situation is that, as γ → ∂ (as an even number), we have
taking only the largest one. In our experience, an SPU(γ) test with γ> 8 often yields results similar to that of the SPU(∞) test. Hence, in all our following experiments, we only used γ ∈ Γ = {1, 2, ..., 8, ∞}.
While the SPU(1) is similar to the Average (Sum) test, the SPU(2) test is the same as the SSU test outlined by Yang and Wang (2012), an extension of the SSU test for single trait–multilocus analysis (Pan 2009) to the current context for multiple traits and a single SNP.
Suppose that the sample size is large enough for the asymptotic null distribution of the score vector to hold, we use a simulation method to estimate the p-value of an SPU test (Seaman and Mller-Myhsok 2005; Lin 2005). Suppose that T is the test statistic for an SPU(γ) test and is the covariance matrix of the score vector based on the original data. We draw B samples of the score vector from its null distribution: , b = 1, ...B, and obtain a null statistic . We then calculate .
Since the result of an SPU(γ) test depends on the choice of the power parameter γ while in general it is unknown which value of is optimal for a given dataset, it would be convenient to have a test that data-adaptively and automatically chooses the parameter γ. We propose an adaptive SPU (aSPU) test to estimate and thus select the most powerful SPU test for given data. Because it is di cult to characterize the power curve of an SPU test, we use the p-value of a SPU test to approximate its power; this idea has been widely used in practice. Accordingly, the aSPU test statistic is the minimum p-value among all SPU tests:
where PSPU(γ) is the p-value of the SPU(γ) test.
The p-value of aSPU can be obtained based on simulations. It may appear that a double simulation procedure is needed, but indeed not necessary. As before, first, we simulate B independent copies of the null score vector U(b) from for b = 1, 2, ..., B. We then calculate the corresponding SPU test statistics and their p-values . Thus, we have , and the final p-value of the aSPU test is . Note that, in practice we can first use a smaller B, say B = 1000, to scan a genome, then gradually and repeatedly increase B for a few SNPs that pass an initial significance criterion (e.g. p-value < 5/B) in the previous step.
The aSPU test aims to data-adaptively approximate the most powerful SPU test among a set of versatile SPU(γ) tests with various values of γ, thus maintaining high power at any given situation. Although we use the minimum p-value to approximate the most powerful SPU test, other combining methods (e.g. Pan et al 2010) are also possible and may be explored. The aSPU test uses adaptive weights on the multiple traits to assess their aggregated e ects (while down-weighting the e ects of null traits).
The SPU and aSPU tests assume that the multiple traits are in the same scale; if not, e.g. when the variances of the traits vary a lot, one should first standardize the traits to have an equal sample variance. For example, when some null traits have larger variances than that of associated traits, an SPU test statistic will be dominated by the noises in the score components for the null traits, leading to concealing association signals and thus reduced power. Alternatively, to account for possibly different scales or variances of the multiple traits, one can use a variance-weighted SPU test (SPUw): for any γ ∈ Γ,
Note that under the working independence model (Rw = I) in GEE, the SPUw(∞) test is equal to the UminP test. The adaptive SPUw (aSPUw) test can be accordingly defined as for the aSPU test.
2.4 Properties of the GEE Tests
We analyze how the proposed GEE-based tests are related to some existing tests in the absence of covariates while testing for association between a set of quantitative traits and a single SNP. By default (unless specified otherwise), we assume without loss of generality that both Yi and xi have been centered at 0; that is, and . For simplicity we also assume that there is no missing data, and each subject has all k traits observed.
We expect that most of our below conclusions can be extended to the case for quantitative traits with covariates Zi: we first regress Yi on Zi to obtain residuals rY,i, and regress xi on Zi to obtain residuals rX,i; then we apply the same arguments below to regression of rY,i on rX,i (instead of regression of Yi on xi).
2.4.1 Fitting a GEE Working Independence Model and an Equivalent Model
In the current context, the GEE model is
| (4) |
with β = (β1, ..., βk)′. Note that, due to centering both Yi and xi at mean 0, no intercept term is needed. To test H0: β = 0, under the working independence model (i.e. Rw = I), we have the score vector and its empirical covariance estimate as
| (5) |
As an alternative, we fit the below model:
| (6) |
with b = (b1, ..., bk)′. To test H0: b = 0, we obtain its score vector and empirical covariance estimate, which are exactly the same as in equation (5). Note that, due to the possible correlations among the components of Yi and possibly non-Normality or non-constant variances of xi (the latter of which is true because xi is the genotype score), we have to use the empirical covariance estimate of the score vector. In summary, any test based on the score vector of fitting the GEE working independence model (4) can be equally constructed based on fitting a simple linear model (6). For example, a GEE-SPU(2) test based on the GEE model (4) is equivalent to the SSU test based on model (6) (Pan 2009).
We note that using the GEE score components and their variances to test for Hm,0: βm = 0 separately for each trait m is the same as conducting a univariate Score test on each trait m individually. Hence, in addition to UminP, other methods could be applied to combine these univariate tests (Yang and Wang 2012); in fact, if Rw = I is used in GEE, all our proposed tests could be regarded in this way.
Finally, we note that the above conclusion holds for other GLMs with a canonical link function, under which the score vector maintains the same form as in (5) (McCullagh and Nelder 1983).
2.4.2 GEE-SPU versus GEE-SPUw tests
In the current context, based on (5), we have
where the Hardy-Weinberg equilibrium is assumed in the second equality for Var(yij), f is the MAF of the SNP, and is the residual variance of trait j (after removing the e ect of the SNP). We also assume that Var(yij) does not depend on i (but may depend on j).
It is clear that the SPUw tests, but not SPU tests, are invariant to the scales of the traits. Hence, the SPUw and aSPUw tests can automatically account for different scales of the multiple traits, while the SPU and aSPU tests cannot, requiring one to standardize the (residual) variances of the traits if they di er a lot. On the other hand, if are all equal, for an associated trait j with βj ≠ = 0, due to its larger Var(yij), any SPUw test would put a lower weight on it as compared to the corresponding SPU test, leading to power loss. However, for complex traits with typically small |βj|, the power loss of the SPUw or aSPUw test is often negligible, resulting in almost equal power between the aSPUw and aSPU tests, as to be confirmed in our numerical examples.
2.4.3 Use of various working correlation structures in GEE
For quantitative traits, it is often reasonable to assume that the marginal covariance matrix Cov(Yi|H0) = V0 does not vary over i. Under this assumption (and thus a equal cluster size dim(Yi) = k), we can write the working covariance matrix Vw,i = Ai−1/2RwAi−1/2 = Vw,0, invariant to i. With any working correlation matrix Rw, the score vector and its covariance estimate are
| (7) |
from which it can be seen that
That is, the GEE-Score test is invariant to Rw, the working correlation structure.
Since in general U(Rw) ≠ U(I) and for Rw ≠ = I, the other GEE-based tests (except GEE-Score) are not necessarily invariant to Rw.
Surprisingly, as to be shown, the GEE-UminP, GEE-SPUw(∞) and GEE-SPU(∞) tests may lose power when the true correlation structure is used as Rw. Here we consider a simple example. Suppose that the first 5 traits are associated with a SNP while all other remaining k−5 traits are not; the true covariance matrix Cov(Yi) has a compound symmetry structure CS(r): Var(yij) = 1 and Cov(yij, yil) = r for any j ≠ l. The score vector U(Rw) = (U1(Rw), . . ., Uk(Rw))′ is defined in (8) and . Without loss of generality, we also assume xi is standardized to have . Under the working independence model Rw = I, assume that E(Uj(I)) = 1 for 1 ≤ j ≤ k1, and E(Uj(I)) = 0 for 5 < j k. Hence, with Rw = I, the component-wise signal magnitude (related to the non-centrality parameter for a univariate Score test on each trait) is
which is 1 for 1 ≤ j ≤ 5, and is 0 otherwise. On the other hand, in the ideal case with Vw = Cov(Yi), we have
Accordingly, we can calculate its component-wise signal magnitude λj = E(Uj(Rw ))2/Var(Uj(Rw)). Table 1 shows some examples.
Table 1.
Component-wise signal magnitude with various Rw and k in GEE.
| Rw | I | R0: CS(r = 0.5) | R0: CS(r = –0.5) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| k | ≥ 5 | 5 | 10 | 40 | 400 | 5 | 10 | 40 | 400 |
| E(U1) | 1 | 0.3 | 1.091 | 1.756 | 1.975 | −1 | 0.191 | 0.577 | 0.658 |
| Var(U1) | 1 | 1.667 | 1.818 | 1.951 | 1.995 | 0.333 | 0.571 | 0.649 | 0.665 |
| λ 1 | 1 | 0.067 | 0.655 | 1.581 | 1.955 | 3.000 | 0.064 | 0.513 | 0.652 |
| E(U6) | 0 | - | −0.909 | −0.244 | −0.025 | - | −0.476 | −0.090 | −0.008 |
| Var(U6) | 1 | - | 1.818 | 1.951 | 1.995 | - | 0.571 | 0.649 | 0.665 |
| λ 6 | 0 | - | 0.455 | 0.031 | 0.0003 | - | 0.397 | 0.013 | 0.0001 |
| 1 | 0.067 | 0.655 | 1.581 | 1.955 | 3.000 | 0.397 | 0.513 | 0.652 | |
It is clear that, compared to using Rw = I, one may gain or lose with respect to componentwise information contents in the score vector by using a correct correlation matrix as Rw in GEE, depending on the value of between-trait correlation r and the number of traits k. In particular, with r > 0 and a small k, using a correct correlation matrix may give maxj λj < 1, leading to loss of power by the UminP test, as compared to its using the working independence model in GEE; as k increases (while keeping the number of associated traits fixed), it will gain by using the correct correlation matrix as Rw. This latter point is consistent with the theoretical result of Cai et al (2013) for a high-dimensional two-sample comparison problem.
2.4.4 Relationships between the new and existing tests
Our proposed tests cover several commonly used methods as special cases in the current context. A summary is given in Table 2, and the details are relegated to the Appendix.
Table 2.
Relationships between the existing and new tests.
| Method | Model or test statistic | Relation to the new tests |
|---|---|---|
| The Average method (Shen et al 2011) | , Applying the Score test on H0: α1 = 0. | Average = GEE-SPU(1). |
| TATES (van der Sluis et al 2013) | Yij = β0,j + β1,jxi + eij for j = 1, 2, ..., k. Testing for H0: β1,1 = ... = β1,k = 0 with analytical approximations to calculate a p-value. | TATES ≈ GEE-UminP ≈ GEE-SPUw(∞). |
| CCA=MANOVA (Ferreira & Purcell 2009; Yang & Wang 2012) | CCA seeks to maximize the correlation between a linear combination of (Yi1, ..., Yik) and xi. Test statistic: | CCA=MANOVA=GEE-Score. |
| MDMR (Zapala & Schork 2012) | , G = (I – 11′/n)A(I – 11′/n), H = X(X′X)–1X′, Test statistic: F = tr(HGH)/tr[(I – H)G(I – H)] | MDMR=GEE-SPU(2) if d(,) is Euclidean. |
| KMR (Maity et al 2012) | Test statistic: | KMR = GEE-SPU(2) if K = XX′ and Rw = Corr(Yi|H0). |
| MultiPhen (O'Reilly et al., 2012) | for j = 0, 1, 2, for j = 0 and 1. Applying the Score (or likelihood ratio) test on H0: β = 0. | MultiPhen ≈ GEE-Score. |
| Generalized Kendall's tau (Zhang et al 2010) | uij = (Yi1 – Yj1, ..., Yiq – Yjq)′, . Test statistic: . | GK-tau = GEE-Score. |
2.5 Simulation Set-ups
Unless specified otherwise, by default each simulated dataset consisted of n = 1000 subjects with a varying number (k) of correlated quantitative traits, including the first k1 = 5 traits associated with the SNPs to be tested under the alternative hypothesis H1 (while all other k − k1 traits were not associated). For each subject, we generated a block of p = 11 SNPs in linkage disequilibrium (LD) and the first one was the causal SNP under H1. Specifically, for each subject i, we first generated a latent vector Gi = (Gi1, ...Gip)′ from a multivariate Normal distribution with a first-order auto-regressive (AR-1) covariance structure with parameter ρ = 0.5: Cov(Gij, Gil) = ρ|j−l|. Second, each latent element Gij was dichotomized to 0 or 1 with probability Prob(Gig = 1) as its minor allele frequency (MAF), randomly drawn from a uniform distribution (Pan 2009). The MAF of the causal (i.e. first) SNP was from U(0.3, 0.4), while the MAFs of the other SNPs were independently drawn from U(0.1, 0.5). In this way, we generated a haplotype for subject i. Similarly, we independently generated another haplotype for subject i; by combining the two haplotypes we obtained the genotype of the subject. We tested on each of the first few SNPs nearest to the causal SNP.
Similarly, we also considered smaller sample sizes n = 500 and n = 200, and rare variants (RVs) with MAF=0.01.
The phenotype for each subject i, Yi = (Yi1, ..., Yik)′ was simulated from a linear model:
where β0 = (β01, ..., β0k)′, β = (β1, ..., βk)′, xi is the genotype score of the causal SNP, and ∈i was independently drawn form a multivariate Normal distribution N(0, σ2R), with σ = 1 and R as either an AR-1 correlation matrix with parameter r or a compound symmetry (CS) matrix with parameter r; we considered r = ±0.3 or 0.5. In addition, we also considered using a correlation matrix estimated from the ADNI data. β0m is the intercept for trait m. Under H0, we had β = 0; under H1, we had βm ≠ = 0 for 1 ≤ m ≤ k1, and βm = 0 for k1 < m ≤ k. The non-zero βj's were randomly drawn from a uniform distribution U(0.2, 0.3) for weak e ects, or from U(0.8, 1) for strong e ects. That is, under H1, only the first 5 traits were associated with the causal SNP, and we gradually increased the number of the non-associated (i.e. null) traits from 0 to 5, then 15, up to 35. Under each simulation set-up, 1000 datasets were independently generated and analyzed; we used B=1000 to obtain p-values for any simulation-based method. Unless specified otherwise, by default, the working independence model was used in GEE.
For comparison, in addition to the GEE-based tests, we also applied some representative existing tests, including the Average method, MultiPhen, TATES, MANOVA (based on the Wilks statistic) and MDMR (based on the L1-norm or L2-norm as the distance metric).
2.6 ADNI Data
Data used in the preparation of this article were obtained from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public-private partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer's disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their e ectiveness, as well as lessen the time and cost of clinical trials. The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California - San Francisco. ADNI is the result of e orts of many coinvestigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. To date these three protocols have recruited over 1500 adults, ages 55 to 90, to participate in the research, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow up duration of each group is specified in the protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see www.adni-info.org.
3 Results
3.1 Simulations
3.1.1 CS
In Table 3, the multivariate traits had a compound symmetry (CS) correlation structure with parameter r = 0.3 or 0.5. All the tests, except the GEE-Wald test, could control the Type I error. As the number of the traits, k, increased, the GEE-Wald test gradually had a severely inflated Type I error; in contrast, the GEE-Score test performed satisfactorily. The poor performance of the Wald test and better performance of the Score test for finite-samples in GEE are well known (e.g. Guo et al 2005); due to its inability to control Type I errors, we will omit the discussion on the GEE-Wald test in the sequel.
Table 3.
Empirical Type I error rates when the multiple traits were correlated with a CS structure with correlation coefficient r. An independence working correlation structure was used in GEE.
| GEE |
|||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MDMR |
SPU(γ) |
||||||||||||||||||
| r | SNP | #traits | Average | MultiPhen | TATES | L 1 | L 2 | MANOVA | Wald | Score | UminP | γ = 1 | 2 | 3 | 4 | 5 | 6 | ∞ | aSPU |
| 0.3 | 1 | 5 | 0.043 | 0.051 | 0.048 | 0.040 | 0.048 | 0.051 | 0.056 | 0.051 | 0.046 | 0.038 | 0.049 | 0.050 | 0.045 | 0.048 | 0.049 | 0.049 | 0.050 |
| 10 | 0.053 | 0.060 | 0.055 | 0.059 | 0.058 | 0.060 | 0.076 | 0.060 | 0.053 | 0.049 | 0.057 | 0.051 | 0.049 | 0.047 | 0.052 | 0.046 | 0.051 | ||
| 20 | 0.058 | 0.062 | 0.046 | 0.052 | 0.046 | 0.064 | 0.094 | 0.062 | 0.046 | 0.054 | 0.048 | 0.046 | 0.049 | 0.051 | 0.049 | 0.046 | 0.047 | ||
| 30 | 0.049 | 0.034 | 0.047 | 0.059 | 0.052 | 0.036 | 0.102 | 0.034 | 0.042 | 0.051 | 0.049 | 0.051 | 0.052 | 0.049 | 0.045 | 0.045 | 0.049 | ||
| 40 | 0.053 | 0.055 | 0.059 | 0.055 | 0.058 | 0.061 | 0.165 | 0.054 | 0.059 | 0.053 | 0.059 | 0.061 | 0.061 | 0.062 | 0.064 | 0.057 | 0.054 | ||
| 0.3 | 2 | 5 | 0.051 | 0.058 | 0.059 | 0.054 | 0.051 | 0.059 | 0.066 | 0.058 | 0.056 | 0.050 | 0.049 | 0.051 | 0.048 | 0.053 | 0.050 | 0.053 | 0.050 |
| 10 | 0.050 | 0.046 | 0.043 | 0.044 | 0.048 | 0.047 | 0.061 | 0.046 | 0.047 | 0.050 | 0.042 | 0.047 | 0.046 | 0.048 | 0.046 | 0.050 | 0.045 | ||
| 20 | 0.048 | 0.049 | 0.048 | 0.048 | 0.048 | 0.049 | 0.078 | 0.049 | 0.048 | 0.049 | 0.054 | 0.053 | 0.051 | 0.053 | 0.055 | 0.046 | 0.053 | ||
| 30 | 0.041 | 0.048 | 0.045 | 0.041 | 0.039 | 0.050 | 0.102 | 0.048 | 0.045 | 0.045 | 0.041 | 0.042 | 0.039 | 0.041 | 0.042 | 0.050 | 0.043 | ||
| 40 | 0.058 | 0.051 | 0.044 | 0.056 | 0.059 | 0.053 | 0.153 | 0.049 | 0.051 | 0.055 | 0.055 | 0.055 | 0.051 | 0.050 | 0.046 | 0.049 | 0.052 | ||
| 0.5 | 1 | 5 | 0.043 | 0.052 | 0.050 | 0.044 | 0.045 | 0.051 | 0.056 | 0.051 | 0.045 | 0.038 | 0.041 | 0.046 | 0.049 | 0.046 | 0.047 | 0.047 | 0.048 |
| 10 | 0.053 | 0.060 | 0.045 | 0.049 | 0.049 | 0.060 | 0.076 | 0.060 | 0.048 | 0.047 | 0.049 | 0.054 | 0.053 | 0.050 | 0.048 | 0.051 | 0.048 | ||
| 20 | 0.058 | 0.062 | 0.048 | 0.057 | 0.051 | 0.064 | 0.094 | 0.062 | 0.055 | 0.055 | 0.053 | 0.049 | 0.048 | 0.050 | 0.047 | 0.052 | 0.048 | ||
| 30 | 0.049 | 0.034 | 0.045 | 0.055 | 0.055 | 0.036 | 0.102 | 0.034 | 0.055 | 0.054 | 0.048 | 0.050 | 0.054 | 0.054 | 0.053 | 0.062 | 0.055 | ||
| 40 | 0.053 | 0.055 | 0.048 | 0.055 | 0.060 | 0.061 | 0.165 | 0.054 | 0.051 | 0.055 | 0.058 | 0.060 | 0.059 | 0.058 | 0.056 | 0.054 | 0.055 | ||
| 0.5 | 2 | 5 | 0.051 | 0.059 | 0.054 | 0.055 | 0.050 | 0.059 | 0.066 | 0.058 | 0.049 | 0.050 | 0.052 | 0.050 | 0.050 | 0.049 | 0.045 | 0.049 | 0.051 |
| 10 | 0.050 | 0.046 | 0.045 | 0.047 | 0.053 | 0.047 | 0.061 | 0.046 | 0.047 | 0.050 | 0.048 | 0.045 | 0.049 | 0.046 | 0.046 | 0.047 | 0.046 | ||
| 20 | 0.048 | 0.049 | 0.046 | 0.045 | 0.048 | 0.049 | 0.078 | 0.049 | 0.048 | 0.049 | 0.051 | 0.050 | 0.055 | 0.056 | 0.054 | 0.049 | 0.048 | ||
| 30 | 0.041 | 0.048 | 0.043 | 0.042 | 0.037 | 0.050 | 0.102 | 0.048 | 0.046 | 0.043 | 0.040 | 0.040 | 0.039 | 0.041 | 0.042 | 0.051 | 0.046 | ||
| 40 | 0.058 | 0.051 | 0.040 | 0.059 | 0.057 | 0.053 | 0.153 | 0.049 | 0.046 | 0.056 | 0.058 | 0.057 | 0.054 | 0.054 | 0.054 | 0.048 | 0.051 | ||
Table 9 shows the power performance of the tests when the causal SNP had strong genetic e ects on the associated 5 traits. Since the causal SNP and its nearest neighbor were strongly associated with (a subset of) the traits, the power of each test was close to 1 (not shown); hence, we tested on the second and third nearest SNPs next to the causal SNP. First, we can empirically verify our theoretical results derived earlier: i) the equivalence between MANOVA and the GEE-Score test, between MDMR(L2) and the GEE-SPU(2) test, and the Average and GEE-SPU(1) tests; ii) the similar performance between TATES and UminP (or SPUw(∞)), and between MultiPhen and the GEE-Score test. Since the traits had a multivariate Normal distribution, using the L2-norm as the distance was more powerful than using the L1-norm in MDMR; however, with other trait distributions, it is possible that the latter may edge over the former. Second, we note that the Average test, or equivalently the GEE-SPU(1) test, had the highest power when all k = k1 = 5 traits were associated with the causal SNP (with similar e ect sizes and the same e ect direction); however, they quickly lost power as k increased, i.e. more non-associated traits were included. Third, as k increased, an SPU(γ) test with a larger γ had higher power than those with smaller γ. In particular, we highlight the case with k = 40: the power of the GEE-SPU(1) or GEE-SPU(2) test could be much lower than GEE-SPU(6) or SPU(∞); for example for SNP 2 and r = 0.3, the SPU(1), SPU(2) and SPU(6) tests had power as 0.084, 0.432 and 0.680 respectively. We also note that GEE-SPU(6) and SPU(∞) gave similar power, implying that using up to 6 or 8 (as done here) is good enough. Fourth, we see that, for any given situation, one of the SPU tests had high power, though its identity changed with the situation. Most importantly, the aSPU test seemed to be able to remain (nearly) most powerful across all situations.
Table 9.
Empirical power when the multiple traits were correlated with a CS(0.3) structure; the first five traits were associated with a causal SNP with log-ORs βj ~ U(0.8, 1), while all others had βj = 0. An independence working correlation structure was used in GEE.
| GEE |
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SPU(γ) |
||||||||||||||||
| n | SNP | #Strait | Average | MultiPhen | TATES | MANOVA | Score | UminP | γ = 1 | 2 | 3 | 4 | 5 | 6 | ∞ | aSPU |
| 500 | 2 | 5 | 0.610 | 0.369 | 0.534 | 0.370 | 0.366 | 0.509 | 0.604 | 0.598 | 0.580 | 0.563 | 0.557 | 0.542 | 0.505 | 0.577 |
| 10 | 0.316 | 0.389 | 0.427 | 0.393 | 0.386 | 0.419 | 0.318 | 0.528 | 0.507 | 0.530 | 0.514 | 0.510 | 0.479 | 0.495 | ||
| 20 | 0.126 | 0.273 | 0.338 | 0.281 | 0.269 | 0.328 | 0.127 | 0.386 | 0.373 | 0.451 | 0.446 | 0.463 | 0.439 | 0.405 | ||
| 30 | 0.089 | 0.209 | 0.291 | 0.229 | 0.208 | 0.280 | 0.090 | 0.261 | 0.279 | 0.390 | 0.380 | 0.417 | 0.412 | 0.370 | ||
| 40 | 0.071 | 0.188 | 0.256 | 0.203 | 0.186 | 0.250 | 0.067 | 0.191 | 0.207 | 0.318 | 0.299 | 0.356 | 0.361 | 0.333 | ||
| 200 | 2 | 5 | 0.306 | 0.144 | 0.254 | 0.146 | 0.144 | 0.237 | 0.312 | 0.298 | 0.291 | 0.285 | 0.280 | 0.273 | 0.249 | 0.287 |
| 10 | 0.160 | 0.151 | 0.197 | 0.163 | 0.149 | 0.182 | 0.155 | 0.235 | 0.230 | 0.247 | 0.237 | 0.243 | 0.225 | 0.229 | ||
| 20 | 0.087 | 0.104 | 0.145 | 0.117 | 0.102 | 0.135 | 0.087 | 0.159 | 0.163 | 0.198 | 0.201 | 0.209 | 0.199 | 0.180 | ||
| 30 | 0.066 | 0.070 | 0.122 | 0.089 | 0.068 | 0.116 | 0.066 | 0.104 | 0.121 | 0.155 | 0.158 | 0.168 | 0.163 | 0.146 | ||
| 40 | 0.054 | 0.063 | 0.087 | 0.091 | 0.060 | 0.077 | 0.053 | 0.081 | 0.089 | 0.123 | 0.121 | 0.140 | 0.139 | 0.122 | ||
Between an SPU(γ) and SPUw(γ) tests for a fixed γ, the former one was more powerful (not shown). As analyzed in section 2, this was presumably due to the larger e ect sizes of the associated traits, giving lower weights to associated SNPs in an SPUw(γ) test than in an SPU(γ). Accordingly, the aSPU test was also more powerful than the aSPUw test.
Table 5 shows the results with weaker genetic e ects. Now the GEE-Score and related MANOVA and MultiPhen tests were more powerful than the SPU/aSPU tests. Note the puzzling phenomenon: the former tests could have lower power with all k = 5 associated traits than that with some additional non-associated traits; this problem of MANOVA was pointed out by Ferreira and Purcell (2009) and studied by Cole et al (1984). In addition, due to the smaller e ect sizes of the associated SNP, the SPU and SPUw tests, and thus aSPU and aSPUw tests, performed similarly (not shown).
Table 5.
Empirical power when the multiple traits were correlated with a CS structure with correlation coefficient r = 0.3, and non-zero βj ~ U(0.2, 0.3). An independence working correlation structure was used in GEE.
| GEE |
|||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MDMR |
SPU(γ) |
||||||||||||||||
| SNP | #traits | Average | MultiPhen | TATES | L 1 | L 2 | MANOVA | Score | UminP | γ = 1 | 2 | 3 | 4 | 5 | 6 | ∞ | aSPU |
| l | 5 | 0.664 | 0.468 | 0.551 | 0.653 | 0.652 | 0.469 | 0.468 | 0.531 | 0.660 | 0.658 | 0.636 | 0.609 | 0.597 | 0.569 | 0.533 | 0.632 |
| 10 | 0.263 | 0.574 | 0.452 | 0.441 | 0.506 | 0.576 | 0.573 | 0.437 | 0.267 | 0.501 | 0.460 | 0.493 | 0.472 | 0.481 | 0.444 | 0.456 | |
| 20 | 0.114 | 0.535 | 0.335 | 0.202 | 0.245 | 0.536 | 0.535 | 0.330 | 0.114 | 0.249 | 0.261 | 0.330 | 0.321 | 0.348 | 0.345 | 0.305 | |
| 30 | 0.084 | 0.458 | 0.283 | 0.126 | 0.158 | 0.462 | 0.456 | 0.282 | 0.085 | 0.162 | 0.188 | 0.254 | 0.262 | 0.288 | 0.293 | 0.257 | |
| 40 | 0.058 | 0.412 | 0.252 | 0.089 | 0.103 | 0.421 | 0.409 | 0.250 | 0.058 | 0.100 | 0.128 | 0.180 | 0.192 | 0.236 | 0.263 | 0.211 | |
| 2 | 5 | 0.226 | 0.110 | 0.165 | 0.209 | 0.213 | 0.110 | 0.108 | 0.160 | 0.221 | 0.214 | 0.206 | 0.188 | 0.188 | 0.181 | 0.166 | 0.211 |
| 10 | 0.087 | 0.142 | 0.120 | 0.098 | 0.117 | 0.143 | 0.142 | 0.115 | 0.088 | 0.117 | 0.116 | 0.129 | 0.129 | 0.128 | 0.122 | 0.118 | |
| 20 | 0.064 | 0.132 | 0.085 | 0.074 | 0.083 | 0.135 | 0.131 | 0.091 | 0.064 | 0.086 | 0.089 | 0.099 | 0.097 | 0.098 | 0.095 | 0.089 | |
| 30 | 0.058 | 0.130 | 0.098 | 0.063 | 0.069 | 0.131 | 0.129 | 0.097 | 0.060 | 0.071 | 0.076 | 0.086 | 0.092 | 0.098 | 0.102 | 0.087 | |
| 40 | 0.050 | 0.091 | 0.067 | 0.057 | 0.056 | 0.098 | 0.091 | 0.066 | 0.049 | 0.055 | 0.057 | 0.064 | 0.066 | 0.070 | 0.071 | 0.063 | |
3.1.2 AR-1
Now we consider the case where the multivariate traits had an AR-1 correlation structure. Table 6 shows that all the tests could control the Type I error rates around the nominal level of 0.05 satisfactorily.
Table 6.
Empirical Type I error rates when the multiple traits were correlated with an AR1 structure with correlation coefficient r. An independence working correlation structure was used in GEE.
| GEE |
||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MDMR |
SPU(γ) |
|||||||||||||||||
| r | SNP | #traits | Average | MultiPhen | TATES | L 1 | L 2 | MANOVA | Score | UminP | γ = 1 | 2 | 3 | 4 | 5 | 6 | ∞ | aSPU |
| 0.5 | 1 | 5 | 0.037 | 0.051 | 0.051 | 0.049 | 0.051 | 0.051 | 0.041 | 0.042 | 0.043 | 0.033 | 0.035 | 0.034 | 0.037 | 0.037 | 0.040 | 0.036 |
| 10 | 0.045 | 0.060 | 0.053 | 0.049 | 0.060 | 0.060 | 0.046 | 0.053 | 0.041 | 0.052 | 0.048 | 0.051 | 0.057 | 0.058 | 0.051 | 0.051 | ||
| 20 | 0.060 | 0.059 | 0.046 | 0.040 | 0.059 | 0.064 | 0.041 | 0.044 | 0.059 | 0.048 | 0.055 | 0.052 | 0.053 | 0.047 | 0.043 | 0.050 | ||
| 0.5 | 2 | 4 | 0.048 | 0.058 | 0.052 | 0.060 | 0.058 | 0.059 | 0.041 | 0.040 | 0.050 | 0.045 | 0.042 | 0.041 | 0.041 | 0.041 | 0.040 | 0.040 |
| 10 | 0.062 | 0.047 | 0.044 | 0.053 | 0.047 | 0.047 | 0.062 | 0.056 | 0.063 | 0.062 | 0.056 | 0.057 | 0.053 | 0.058 | 0.064 | 0.061 | ||
| 20 | 0.046 | 0.047 | 0.052 | 0.048 | 0.047 | 0.049 | 0.048 | 0.052 | 0.043 | 0.058 | 0.053 | 0.053 | 0.054 | 0.051 | 0.060 | 0.053 | ||
| 0.3 | 1 | 5 | 0.037 | 0.051 | 0.040 | 0.047 | 0.045 | 0.051 | 0.041 | 0.042 | 0.039 | 0.034 | 0.034 | 0.037 | 0.037 | 0.038 | 0.039 | 0.036 |
| 10 | 0.048 | 0.060 | 0.049 | 0.061 | 0.054 | 0.060 | 0.046 | 0.043 | 0.047 | 0.049 | 0.040 | 0.044 | 0.037 | 0.040 | 0.040 | 0.052 | ||
| 20 | 0.059 | 0.062 | 0.050 | 0.050 | 0.048 | 0.064 | 0.041 | 0.058 | 0.060 | 0.042 | 0.062 | 0.047 | 0.062 | 0.055 | 0.057 | 0.058 | ||
| 0.3 | 2 | 5 | 0.049 | 0.058 | 0.057 | 0.056 | 0.060 | 0.059 | 0.041 | 0.049 | 0.051 | 0.050 | 0.040 | 0.043 | 0.046 | 0.044 | 0.044 | 0.042 |
| 10 | 0.061 | 0.046 | 0.054 | 0.045 | 0.042 | 0.047 | 0.062 | 0.056 | 0.061 | 0.062 | 0.065 | 0.063 | 0.059 | 0.057 | 0.057 | 0.059 | ||
| 20 | 0.051 | 0.049 | 0.044 | 0.050 | 0.047 | 0.049 | 0.048 | 0.062 | 0.051 | 0.058 | 0.051 | 0.053 | 0.056 | 0.059 | 0.062 | 0.056 | ||
For power (Table 7), regardless of the value of r, we reached the same conclusions. First, it is clear that the aSPU test was more powerful than the MultiPhen, TATES, Score and UminP test. As more null traits were added, power of all methods generally decreased and the aSPU test still maintained its advantage. The power of MultiPhen was close to that of the GEE-Score test, while that of TATES was close to that of the UminP test. For example, when testing the association between SNP 1 and k = 5 traits (with no null traits), MultiPhen had a power of 0.458, TATES had 0.554, GEE-Score test had 0.458, UminP had 0.522, while the aSPU test had 0.624, close to 0.661, the highest power given by the Average method, essentially the same as that of SPU(1) test at 0.651. However, as the total number of traits increased to 20 (with 15 null traits), the power of the Averaging method dramatically reduced to 0.217, compared to 0.286 of the GEE-Score test and 0.334 of the UminP, all much lower than 0.400 of the aSPU test. The results also confirmed that if the SNP of interest was physically farther away from the causal SNP, the power any test would be largely reduced. For example, when testing SNP 1 based on 10 traits, the power of the Score test was 0.388 and the aSPU was 0.516; but when testing SNP 2, their power decreased to 0.100 and 0.139 respectively.
Table 7.
Empirical power when the multiple traits were correlated with an AR1 structure with correlation coefficient r; the non-zero βj ~ U(0.2, 0.3). An independence working correlation structure was used in GEE.
| GEE |
||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MDMR |
SPU(γ) |
|||||||||||||||||
| r | SNP | #traits | Average | MultiPhen | TATES | L 1 | L 2 | MANOVA | Score | UminP | γ = 1 | 2 | 3 | 4 | 5 | 6 | ∞ | aSPU |
| 0.5 | 1 | 5 | 0.661 | 0.458 | 0.554 | 0.629 | 0.634 | 0.459 | 0.458 | 0.522 | 0.651 | 0.630 | 0.624 | 0.594 | 0.582 | 0.564 | 0.525 | 0.624 |
| 10 | 0.390 | 0.371 | 0.426 | 0.496 | 0.527 | 0.373 | 0.388 | 0.447 | 0.388 | 0.555 | 0.534 | 0.533 | 0.513 | 0.513 | 0.471 | 0.516 | ||
| 20 | 0.217 | 0.262 | 0.332 | 0.362 | 0.365 | 0.263 | 0.286 | 0.334 | 0.214 | 0.414 | 0.390 | 0.427 | 0.397 | 0.402 | 0.343 | 0.400 | ||
| 0.5 | 2 | 5 | 0.223 | 0.113 | 0.165 | 0.202 | 0.201 | 0.113 | 0.113 | 0.153 | 0.220 | 0.206 | 0.193 | 0.182 | 0.178 | 0.173 | 0.162 | 0.208 |
| 10 | 0.124 | 0.107 | 0.122 | 0.131 | 0.129 | 0.107 | 0.100 | 0.112 | 0.124 | 0.150 | 0.137 | 0.139 | 0.127 | 0.129 | 0.114 | 0.139 | ||
| 20 | 0.084 | 0.080 | 0.105 | 0.121 | 0.118 | 0.081 | 0.069 | 0.104 | 0.090 | 0.113 | 0.106 | 0.122 | 0.109 | 0.116 | 0.103 | 0.111 | ||
| 0.3 | 1 | 5 | 0.780 | 0.547 | 0.571 | 0.698 | 0.706 | 0.571 | 0.546 | 0.551 | 0.774 | 0.706 | 0.709 | 0.647 | 0.637 | 0.602 | 0.551 | 0.737 |
| 10 | 0.487 | 0.442 | 0.469 | 0.568 | 0.596 | 0.444 | 0.442 | 0.443 | 0.482 | 0.592 | 0.569 | 0.546 | 0.530 | 0.511 | 0.454 | 0.572 | ||
| 20 | 0.274 | 0.309 | 0.366 | 0.448 | 0.490 | 0.312 | 0.307 | 0.349 | 0.277 | 0.478 | 0.456 | 0.467 | 0.438 | 0.434 | 0.368 | 0.459 | ||
| 0.3 | 2 | 5 | 0.245 | 0.129 | 0.154 | 0.177 | 0.179 | 0.129 | 0.127 | 0.146 | 0.244 | 0.180 | 0.185 | 0.165 | 0.164 | 0.153 | 0.149 | 0.190 |
| 10 | 0.147 | 0.120 | 0.129 | 0.157 | 0.156 | 0.121 | 0.119 | 0.122 | 0.146 | 0.161 | 0.146 | 0.143 | 0.139 | 0.136 | 0.122 | 0.156 | ||
| 20 | 0.077 | 0.085 | 0.093 | 0.121 | 0.126 | 0.087 | 0.085 | 0.087 | 0.078 | 0.131 | 0.113 | 0.115 | 0.098 | 0.103 | 0.091 | 0.113 | ||
It is confirmed that the SPU and SPUw tests, and thus aSPU and aSPUw tests, were always almost equally powered, presumably due to the small e ect sizes here (not shown). Given that the majority of common SNPs that are associated with common diseases and other complex traits have only small e ect sizes, we conclude that it is unlikely that the aSPU and aSPUw tests would perform much di erently in practice; we recommend the use of the aSPU test (after standardizing the correlated traits to the same scale if needed).
When the causal SNP had di erent e ect directions on di erent traits, and/or when the correlations among the multiple traits were possibly negative, it was confirmed that the Average, SPU(1), SPUw(1) (and more generally, any SPU(γ) or SPUw(γ) test with γ as an odd number) would lose power; the better performance of the GEE-Score (and related tests) over that of aSPU, or vice versa, depended on the situations (not shown), as previously shown for the cases with a CS correlation structure.
3.1.3 Using a more realistic correlation matrix
We also considered using a correlation matrix mimicking real data. Specifically, based on the ADNI data, we fitted a null model (with several covariates but no SNP) to a set of 26 neuroimaging traits and thus estimated their correlation matrix. These traits appeared to be strongly correlated with the first quartile, median and third quartile of pair-wise correlations at 0.34, 0.47 and 0.59 respectively. We generated simulated data as before except fixing the number of the traits at 26 with their true correlation matrix as the one estimated from the ADNI data. As shown in Table 8, under the null hypothesis, it is clear that the methods could control the Type I error rates satisfactorily (except the GEE Wald test, which was omitted). For power, we randomly picked up the first five traits to be associated with a causal SNP; we considered both strong and weak e ects from the causal SNP. The conclusions were the same as before. For example, when the SNP-traits were strongly associated, the aSPU test was more powerful than the Score test. On the other hand, if the causal SNP was weakly associated with the five traits, given that the traits were strongly correlated as for the previous simulation case with a CS structure, the Score test appeared to be more powerful than the aSPU test.
Table 8.
Empirical Type I error rates (for β = 0) and power (for β ≠ 0) for 26 traits with the true correlation matrix estimated from the ADNI data; for β ≠ 0, the first five traits were associated with a causal SNP with log-ORs βj ~ U(0.8, 1) or ~ U(0.2, 0.3), while all others had βj = 0. An independence working correlation structure was used in GEE.
| GEE |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SPU(γ) |
|||||||||||||||
| β | SNP | Average | MultiPhen | TATES | MANOVA | Score | UminP | γ = 1 | 2 | 3 | 4 | 5 | 6 | ∞ | aSPU |
| β = 0 | 1 | 0.054 | 0.037 | 0.051 | 0.039 | 0.037 | 0.053 | 0.055 | 0.048 | 0.048 | 0.053 | 0.053 | 0.050 | 0.056 | 0.056 |
| βj ~ U(0.8, 1) | 2 | 0.116 | 0.565 | 0.614 | 0.574 | 0.564 | 0.618 | 0.113 | 0.416 | 0.501 | 0.659 | 0.650 | 0.711 | 0.716 | 0.679 |
| 3 | 0.064 | 0.126 | 0.143 | 0.132 | 0.125 | 0.147 | 0.060 | 0.098 | 0.123 | 0.162 | 0.172 | 0.183 | 0.220 | 0.176 | |
| βj ~ U(0.2, 03) | 1 | 0.071 | 0.619 | 0.302 | 0.629 | 0.617 | 0.317 | 0.068 | 0.115 | 0.151 | 0.205 | 0.235 | 0.272 | 0.339 | 0.270 |
| 2 | 0.053 | 0.141 | 0.079 | 0.144 | 0.140 | 0.085 | 0.052 | 0.057 | 0.059 | 0.065 | 0.076 | 0.080 | 0.086 | 0.082 | |
3.1.4 Other cases with smaller sample sizes and association parameters
We considered whether the sample size would change our conclusions. We used a smaller sample size n = 500 or n = 200 while the multiple traits had a CS(0.3) correlation matrix. As shown in Table 9, we reached the same conclusions. For example, the aSPU test was more powerful than the Score test in these cases.
So far we have always assumed that the association directions between a causal SNP and multiple traits are in the same direction. Next we considered the case where a subset of the traits were positively while another subset were negatively, and weakly associated with the causal SNP. We still used a CS(r) as the correlation matrix for the traits. As shown in Table 10, as expected, the Average method and any SPU(γ) test with γ being an odd number were always low powered. Between the Score and aSPU tests, if r = 0.3, then the Score test was more powerful; however, if r = −0.3, then the aSPU test was more powerful. Overall, either the Score test or the aSPU test was the winner.
Table 10.
Empirical power when the multiple traits were correlated with a CS(r) structure; the first five traits were associated with a causal SNP with log-ORs βj ~ –(–1)jU(0.2, 0.3), while all others had βj = 0. An independence working correlation structure was used in GEE.
| GEE |
|||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SPU(γ) |
|||||||||||||||||
| r | SNP | #trait | Average | MultiPhen | TATES | Score | UminP | γ = 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ∞ | aSPU |
| SNP 1 | |||||||||||||||||
| 0.3 | 1 | 5 | 0.084 | 0.926 | 0.671 | 0.928 | 0.626 | 0.085 | 0.817 | 0.442 | 0.754 | 0.558 | 0.712 | 0.595 | 0.685 | 0.631 | 0.739 |
| 10 | 0.075 | 0.854 | 0.541 | 0.851 | 0.512 | 0.073 | 0.684 | 0.356 | 0.644 | 0.463 | 0.598 | 0.482 | 0.569 | 0.529 | 0.586 | ||
| 20 | 0.058 | 0.713 | 0.397 | 0.718 | 0.392 | 0.058 | 0.503 | 0.237 | 0.511 | 0.327 | 0.477 | 0.366 | 0.452 | 0.416 | 0.420 | ||
| 2 | 5 | 0.060 | 0.272 | 0.173 | 0.289 | 0.168 | 0.063 | 0.188 | 0.137 | 0.179 | 0.156 | 0.177 | 0.163 | 0.175 | 0.169 | 0.140 | |
| 10 | 0.062 | 0.230 | 0.120 | 0.227 | 0.126 | 0.062 | 0.143 | 0.111 | 0.145 | 0.128 | 0.146 | 0.133 | 0.141 | 0.137 | 0.115 | ||
| 20 0.062 | 0.167 | 0.100 | 0.170 | 0.145 | 0.084 | 0.059 | 0.087 | 0.078 | 0.088 | 0.086 | 0.083 | 0.084 | 0.084 | 0.087 | 0.085 | ||
| –0.3 | 1 | 5 | 0.152 | 0.567 | 0.587 | 0.571 | 0.553 | 0.147 | 0.730 | 0.402 | 0.668 | 0.479 | 0.626 | 0.512 | 0.599 | 0.557 | 0.646 |
| 10 | 0.115 | 0.466 | 0.461 | 0.490 | 0.488 | 0.118 | 0.640 | 0.356 | 0.606 | 0.435 | 0.566 | 0.464 | 0.552 | 0.502 | 0.565 | ||
| 20 | 0.078 | 0.308 | 0.352 | 0.329 | 0.365 | 0.081 | 0.511 | 0.237 | 0.497 | 0.316 | 0.458 | 0.340 | 0.435 | 0.375 | 0.426 | ||
| 2 | 5 | 0.075 | 0.117 | 0.137 | 0.144 | 0.165 | 0.073 | 0.212 | 0.135 | 0.186 | 0.150 | 0.168 | 0.148 | 0.165 | 0.159 | 0.163 | |
| 10 | 0.072 | 0.121 | 0.136 | 0.108 | 0.121 | 0.071 | 0.164 | 0.119 | 0.160 | 0.126 | 0.143 | 0.130 | 0.134 | 0.129 | 0.145 | ||
| 20 | 0.057 | 0.091 | 0.118 | 0.080 | 0.076 | 0.055 | 0.113 | 0.069 | 0.096 | 0.072 | 0.092 | 0.071 | 0.085 | 0.074 | 0.087 | ||
3.1.5 Rare variants
As suggested by a reviewer, we considered rare variants with MAF fixed at 0.01 when simulating genotypes, while all other aspects were the same as before. To be consistent with our focus here on single SNP testing, we tested on each RV separately, though testing on multiple RVs was expected to be more powerful. As shown in Table 11, the results were pretty much the same as those for common variants when the causal SNP was strongly associated with five traits. For example, it was confirmed again that the results between the Average and GEE-SPU(1), between TATES and GEE-UminP, and among MultiPhen, MANOVA and GEE-Score tests were almost the same respectively. More importantly, the aSPU test was much more powerful than the previous tests, especially as the number of non-associated traits increased.
Table 11.
Empirical Type I error rates (for β = 0) and power (for β ≠ 0) when the multiple traits were correlated with a CS(0.3) structure; for β ≠ 0, the first five traits were associated with a causal RV with log-ORs βj ~ U(7.5, 8), while all others had βj = 0. All the RVs had MAF=0.01. An independence working correlation structure was used in GEE.
| GEE |
||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SPU(γ) |
||||||||||||||||||
| β | SNP | #traits | Average | MultiPhen | TATES | MANOVA | Score | UminP | γ = 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ∞ | aSPU |
| β = 0 | 1 | 5 | 0.060 | 0.052 | 0.056 | 0.052 | 0.052 | 0.055 | 0.062 | 0.052 | 0.055 | 0.050 | 0.050 | 0.050 | 0.055 | 0.057 | 0.057 | 0.052 |
| 10 | 0.049 | 0.055 | 0.047 | 0.056 | 0.055 | 0.042 | 0.049 | 0.050 | 0.051 | 0.049 | 0.047 | 0.048 | 0.047 | 0.049 | 0.043 | 0.043 | ||
| 20 | 0.040 | 0.042 | 0.041 | 0.042 | 0.041 | 0.045 | 0.042 | 0.037 | 0.037 | 0.040 | 0.041 | 0.044 | 0.046 | 0.046 | 0.041 | 0.042 | ||
| 30 | 0.047 | 0.048 | 0.051 | 0.049 | 0.047 | 0.051 | 0.049 | 0.054 | 0.055 | 0.054 | 0.059 | 0.058 | 0.057 | 0.056 | 0.057 | 0.057 | ||
| 40 | 0.033 | 0.049 | 0.045 | 0.052 | 0.049 | 0.048 | 0.037 | 0.037 | 0.037 | 0.037 | 0.036 | 0.040 | 0.044 | 0.044 | 0.048 | 0.039 | ||
| β ≠ 0 | 1 | 5 | 0.702 | 0.587 | 0.677 | 0.587 | 0.587 | 0.679 | 0.696 | 0.697 | 0.698 | 0.693 | 0.688 | 0.684 | 0.681 | 0.680 | 0.674 | 0.691 |
| 10 | 0.596 | 0.551 | 0.634 | 0.552 | 0.550 | 0.624 | 0.594 | 0.688 | 0.684 | 0.698 | 0.694 | 0.695 | 0.690 | 0.689 | 0.680 | 0.679 | ||
| 20 | 0.421 | 0.513 | 0.613 | 0.516 | 0.513 | 0.609 | 0.426 | 0.678 | 0.667 | 0.696 | 0.692 | 0.695 | 0.695 | 0.696 | 0.690 | 0.672 | ||
| 30 | 0.263 | 0.463 | 0.579 | 0.465 | 0.461 | 0.575 | 0.265 | 0.657 | 0.649 | 0.685 | 0.674 | 0.692 | 0.689 | 0.693 | 0.680 | 0.667 | ||
| 40 | 0.163 | 0.403 | 0.546 | 0.409 | 0.401 | 0.539 | 0.160 | 0.599 | 0.602 | 0.669 | 0.663 | 0.679 | 0.679 | 0.682 | 0.677 | 0.648 | ||
3.1.6 Using other working correlation structures in GEE
It is confirmed that using a non-diagonal correlation structure in GEE may or may not improve the performance of the GEE-based tests. For example, when the true CS correlation structure was used as the working one, the performance of the SPU and aSPU tests improved (Table 12); on the other hand, if Rw=CS was used for the case with an AR-1 as the true correlation structure, the power of the SPU and aSPU tests could be lower than that of using Rw = I (Table 12). On the other hand, in the current context, as shown in section 2, the GEE-Score is invariant to the use of Rw. We also note that the UminP and SPU(∞) (and SPUw(∞)) tests could have a severe loss of power with the use of a non-diagonal working correlation structure, even if the working correlation structure was the same as the true CS structure, as analyzed in section 2.
Table 12.
GEE methods with various true and working correlation matrices for non-zero βj ~ U(0.2, 0.3).
| Correlation |
SPU(γ) |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| True | Rw | r | SNP | #traits | Score | UminP | γ = 1 | 2 | 3 | 4 | 5 | 6 | ∞ | aSPU |
| CS | CS | 0.3 | 1 | 5 | 0.468 | 0.155 | 0.662 | 0.163 | 0.278 | 0.164 | 0.202 | 0.159 | 0.152 | 0.565 |
| 10 | 0.594 | 0.374 | 0.294 | 0.595 | 0.385 | 0.513 | 0.375 | 0.447 | 0.375 | 0.536 | ||||
| 20 | 0.535 | 0.352 | 0.116 | 0.603 | 0.394 | 0.544 | 0.387 | 0.476 | 0.365 | 0.521 | ||||
| 30 | 0.456 | 0.362 | 0.084 | 0.530 | 0.416 | 0.512 | 0.412 | 0.466 | 0.374 | 0.487 | ||||
| 2 | 5 | 0.108 | 0.065 | 0.227 | 0.059 | 0.101 | 0.067 | 0.070 | 0.068 | 0.062 | 0.162 | |||
| 10 | 0.133 | 0.108 | 0.102 | 0.144 | 0.102 | 0.138 | 0.102 | 0.127 | 0.113 | 0.135 | ||||
| 20 | 0.131 | 0.103 | 0.067 | 0.155 | 0.105 | 0.133 | 0.097 | 0.114 | 0.099 | 0.112 | ||||
| 30 | 0.129 | 0.123 | 0.060 | 0.138 | 0.109 | 0.144 | 0.119 | 0.133 | 0.122 | 0.120 | ||||
| AR1 | CS | 0.5 | 1 | 5 | 0.458 | 0.158 | 0.661 | 0.121 | 0.293 | 0.143 | 0.188 | 0.146 | 0.173 | 0.559 |
| 10 | 0.371 | 0.296 | 0.345 | 0.422 | 0.363 | 0.369 | 0.316 | 0.345 | 0.307 | 0.442 | ||||
| 20 | 0.261 | 0.264 | 0.196 | 0.337 | 0.337 | 0.337 | 0.317 | 0.321 | 0.293 | 0.368 | ||||
| 2 | 5 | 0.113 | 0.062 | 0.221 | 0.056 | 0.096 | 0.056 | 0.076 | 0.060 | 0.070 | 0.163 | |||
| 10 | 0.107 | 0.102 | 0.116 | 0.109 | 0.094 | 0.107 | 0.092 | 0.103 | 0.096 | 0.123 | ||||
| 20 | 0.080 | 0.094 | 0.065 | 0.124 | 0.113 | 0.115 | 0.099 | 0.106 | 0.100 | 0.121 | ||||
| AR1 | CS | 0.3 | 1 | 5 | 0.546 | 0.248 | 0.778 | 0.297 | 0.458 | 0.276 | 0.338 | 0.261 | 0.251 | 0.699 |
| 10 | 0.442 | 0.323 | 0.486 | 0.468 | 0.482 | 0.424 | 0.402 | 0.387 | 0.325 | 0.549 | ||||
| 20 | 0.307 | 0.291 | 0.273 | 0.423 | 0.424 | 0.399 | 0.374 | 0.361 | 0.312 | 0.445 | ||||
| 2 | 5 | 0.127 | 0.081 | 0.242 | 0.073 | 0.123 | 0.080 | 0.097 | 0.081 | 0.084 | 0.163 | |||
| 10 | 0.119 | 0.118 | 0.147 | 0.133 | 0.129 | 0.130 | 0.122 | 0.119 | 0.108 | 0.146 | ||||
| 20 | 0.085 | 0.084 | 0.080 | 0.126 | 0.111 | 0.116 | 0.095 | 0.103 | 0.088 | 0.125 | ||||
3.1.7 Combining the GEE Score and aSPU tests
It has been shown that, depending on the correlation structure for multiple traits and association parameters between SNPs and traits, one of the GEE Score test and aSPU test was better than the other, but neither could dominate the other across all situations. In light of this result and that in practice it is unknown which test would be more powerful, it might be productive to combine the two tests. A simple strategy is to take the minimum p-value of the two tests, yielding an aSPU.Sco test with test statistic
where PSco is the p-value of the Score test (and PSPU(γ) is the p-value of the SPU(γ) test). To calculate the p-value of the aSPU.Sco test, we do not need another level of resampling; we simply include the Score test along with the SPU tests in the simulation algorithm discussed earlier for the aSPU test.
Table 13 shows the results for the multiple traits with a CS(0.3) correlation matrix. First, it is clear that the new test could maintain a satisfactory Type I error rate. Second, the performance of the new test was always between the other two tests, often closer to the winner. For example, in the case of a causal SNP weakly associated with 5 traits: i) when testing on the five associated traits, the Score test was less power than the aSPU test with their power as 0.464 and 0.632 respectively, while the power of the new test was 0.612, very close to the aSPU test; ii) on the other ahnd, when testing on 10 traits, the power of the Score test was 0.569, larger than 0.456 of the aSPU test, and the new test achieved the power of 0.537, again close to the winner.
Table 13.
Empirical Type I error rates (for β = 0) and power (for β ≠ 0) for the multiple traits with a CS(0.3) correlation matrix; for β ≠ 0, the first five traits were associated with a causal SNP with log-ORs βj ~ U(0.8, 1) or ~ U(0.2, 0.3), while all others had βj = 0. An independence working correlation structure was used in GEE.
|
β = 0 |
βj ~ U(0.2, 0.3) |
βj ~ U(0.1, 1) |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| #traits | Score | aSPU | aSPU.Sco | Score | aSPU | aSPU.Sco | Score | aSPU | aSPU.Sco |
| 5 | 0.051 | 0.050 | 0.051 | 0.468 | 0.632 | 0.612 | 0.682 | 0.865 | 0.832 |
| 10 | 0.060 | 0.051 | 0.059 | 0.573 | 0.456 | 0.537 | 0.684 | 0.795 | 0.777 |
| 20 | 0.060 | 0.047 | 0.048 | 0.535 | 0.305 | 0.463 | 0.611 | 0.757 | 0.741 |
| 30 | 0.032 | 0.049 | 0.042 | 0.456 | 0.257 | 0.394 | 0.528 | 0.703 | 0.693 |
| 40 | 0.054 | 0.054 | 0.057 | 0.409 | 0.211 | 0.321 | 0.424 | 0.639 | 0.628 |
3.2 ADNI data
We applied the methods to the ADNI cohort at baseline, which consisted of 680 non-Hispanic Caucasians with both genotype and phenotype data, including 192 healthy controls, 327 subjects with mild cognitive impairment and 161 patients with Alzheimer's disease. We would like to use a few structural MRI-derived multiple traits as intermediate phenotypes to assess their association with genetic variation. We downloaded from the ADNI website 56 cross-sectional FreeSurfer traits related to volumetric and cortical thickness measures at the baseline as processed by the UCSF team (Hartig et al 2012). For illustration, we only tested 20 SNPs shown by Shen et al (2010) to be marginally significantly associated with one or more of the FreeSurfer traits. Here we considered only 7 multivariate traits consisting of a varying number of univariate traits as shown in Table 14, which were singled out by Shen et al (2010) to be more significantly associated with some of the 20 SNPs. The 7 multivariate traits included each of the six multivariate traits in Table 14 at the right side of the brain plus one of them (MeanPar) at the left side of the brain too. The covariates included were sex, handedness, brain volume, education (in years), and age. There were in total 680 subjects.
Table 14.
Multivariate traits. A letter “L” or “R” is to be added to each trait's ID to indicate the left or right side of the brain.
| Trait ID | Trait description |
|---|---|
| MeanCing | Mean thickness of caudal anterior cingulate, isthmus cingulate, posterior cingulate, and rostral anterior cingulate |
| MeanFront | Mean thickness of caudal midfrontal, rostral midfrontal, superior frontal, lateral orbitofrontal, and medial orbitofrontal gyri and frontal pole |
| MeanLatTemp | Mean thickness of inferior temporal, middle temporal and superior temporal gyri |
| MeanMedTemp | Mean thickness of fusiform, parahippocampal, and lingual gyri, temporal pole and transverse temporal pole |
| MeanPar | Mean thickness of inferior and superior parietal gyri, supramarginal gyrus, and precuneus |
| MeanTemp | Mean thickness of inferior temporal, middle temporal, superior temporal, fusiform, parahippocampal and lingual gyri, temporal pole and transverse temporal pole |
We first used B = 10000 for any simulation-based method (i.e. GEE-UminP, GEE-SPU and GEE-aSPU tests) to calculate p-values. Then for those SNPs with p-value< 5/B, we gradually increased B to 105, then to 106, and finally up to 107 if needed. Other tests used asymptotics to calculate their p-values.
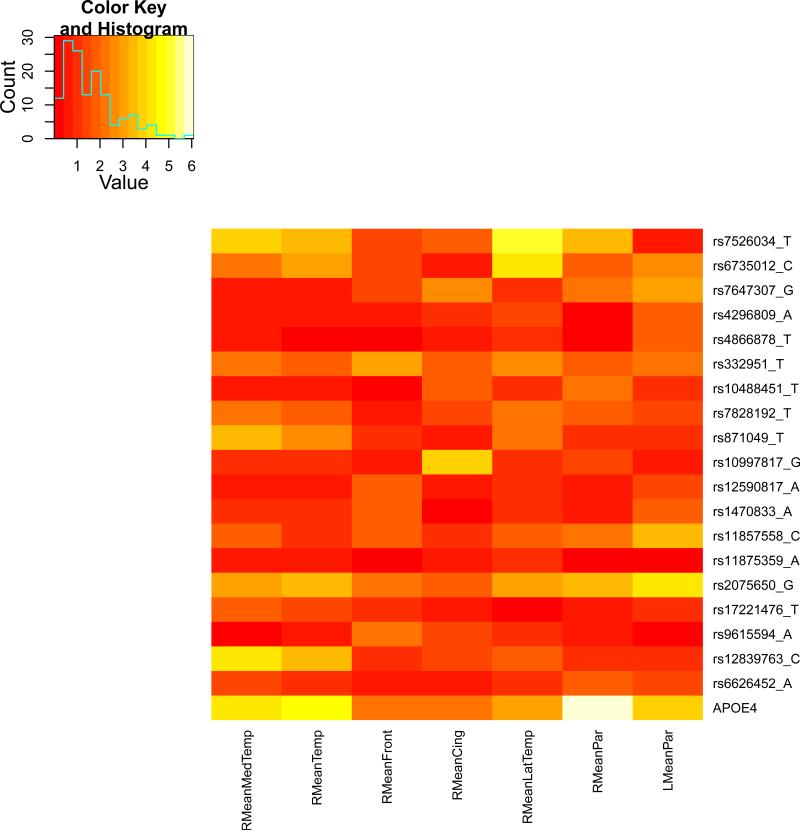
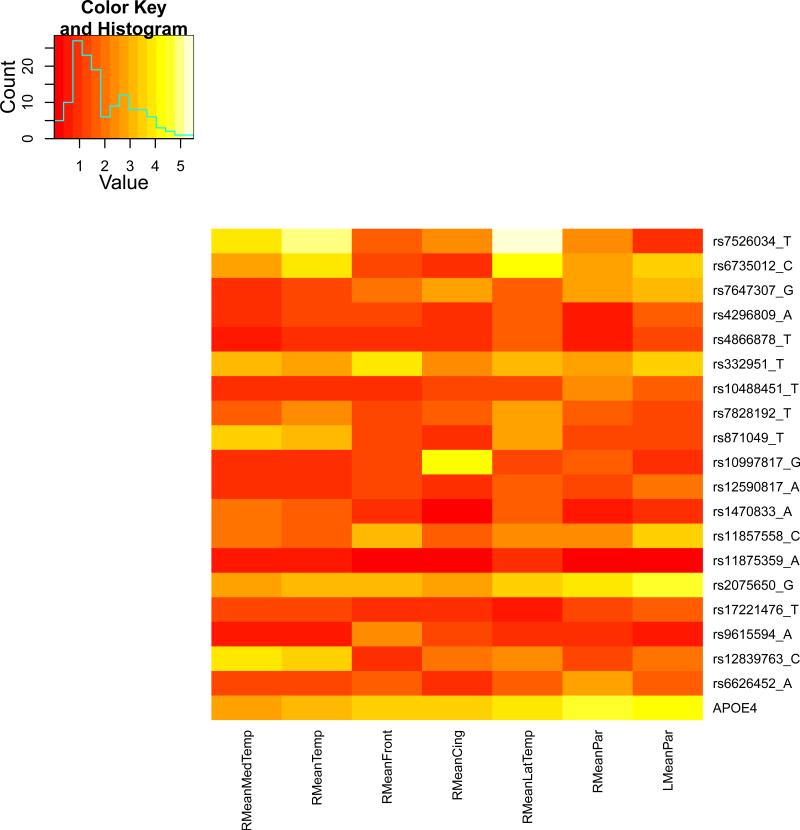
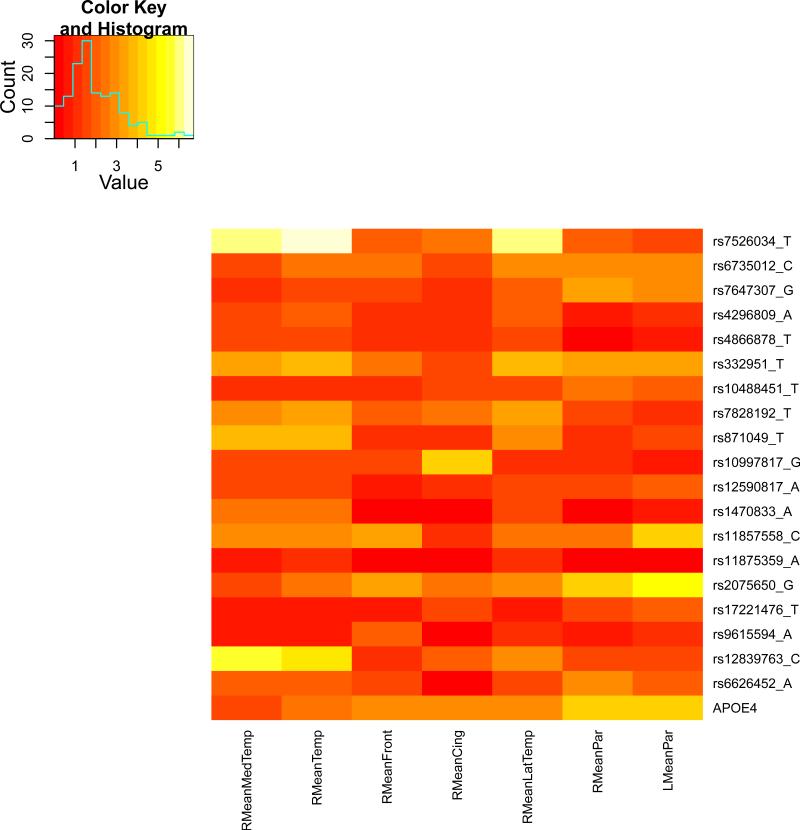
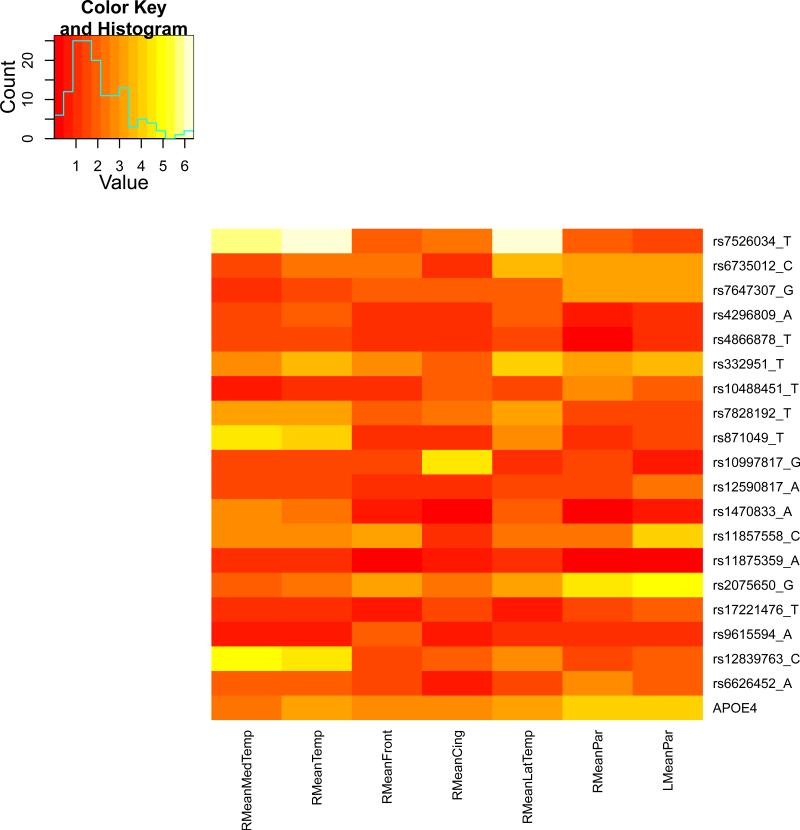
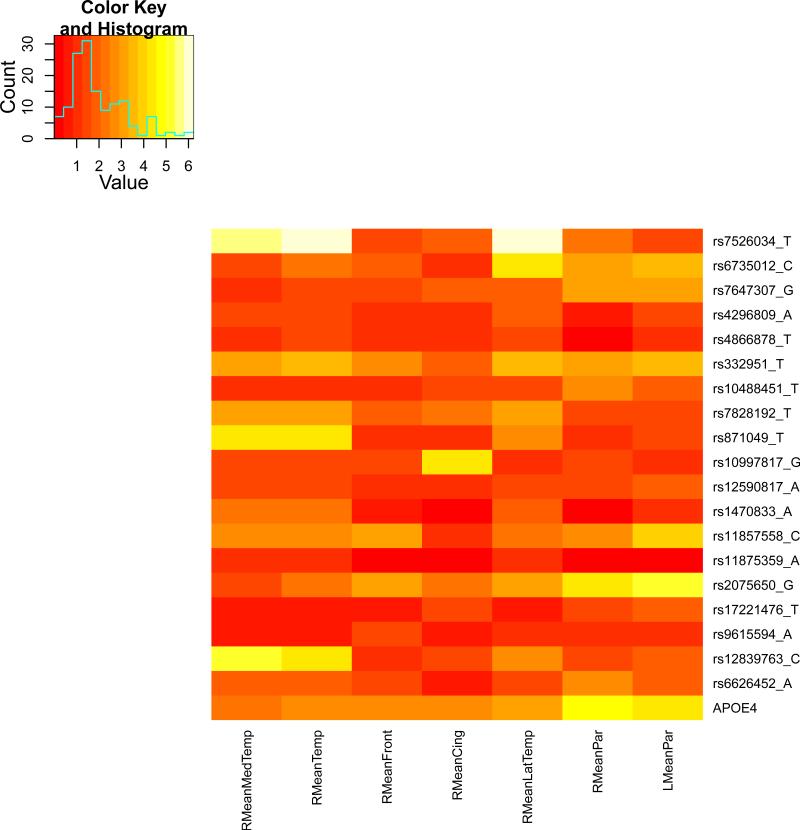
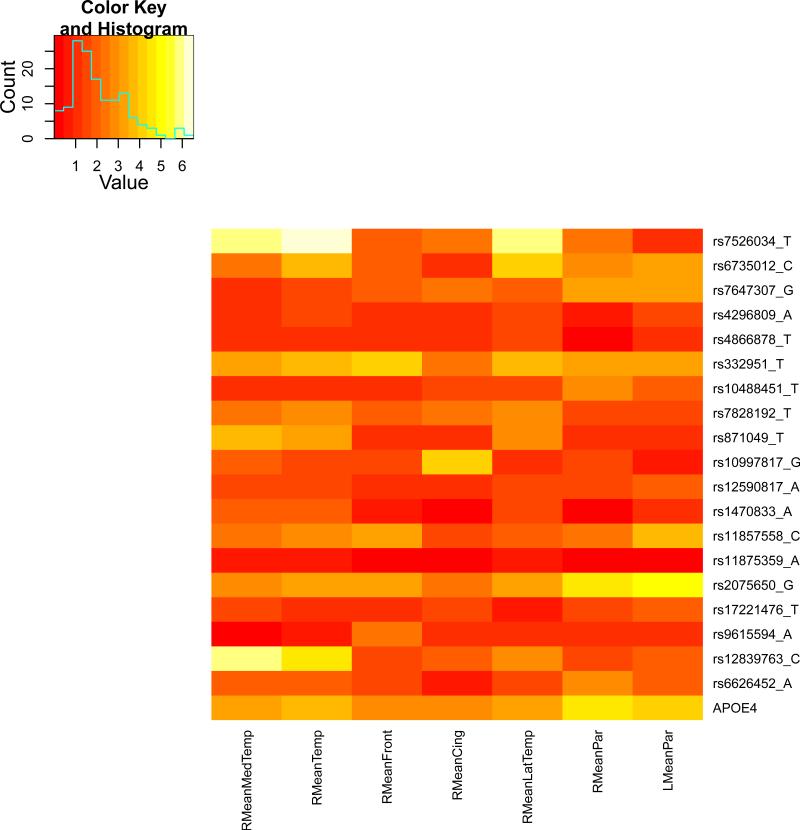
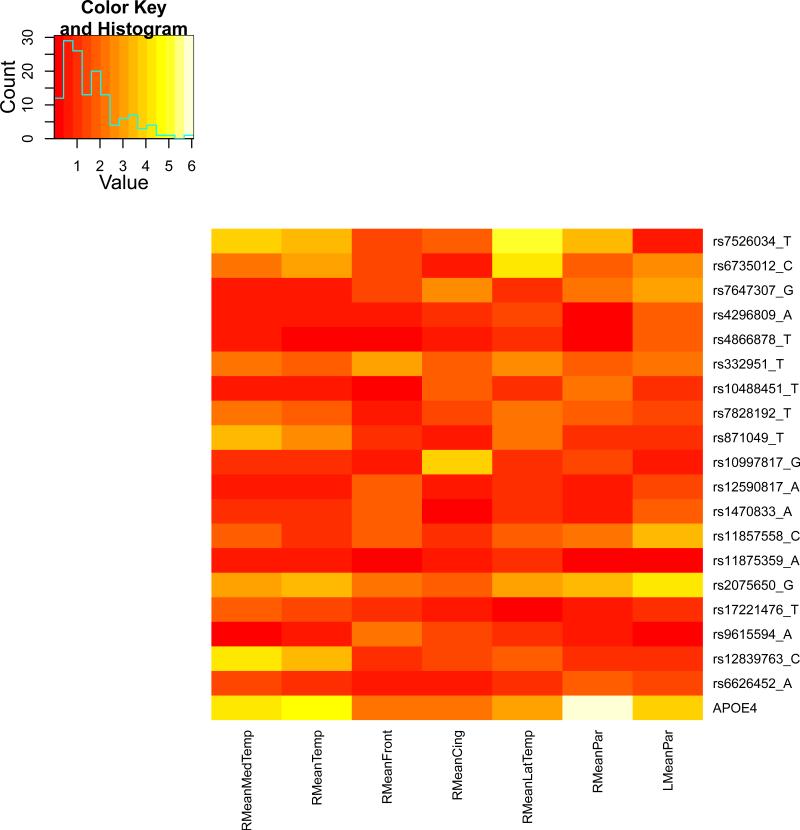
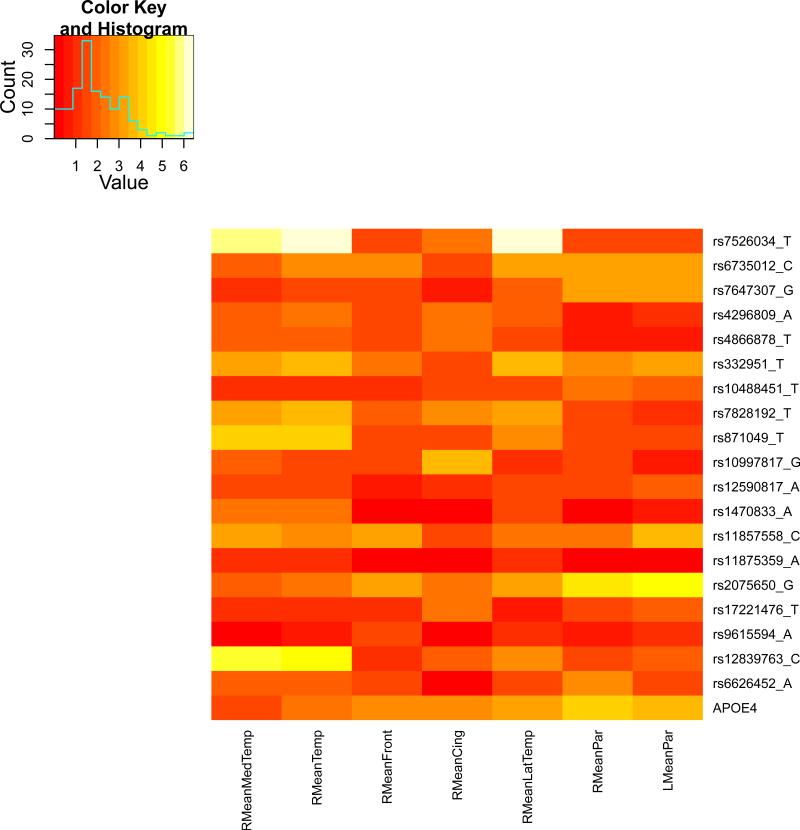
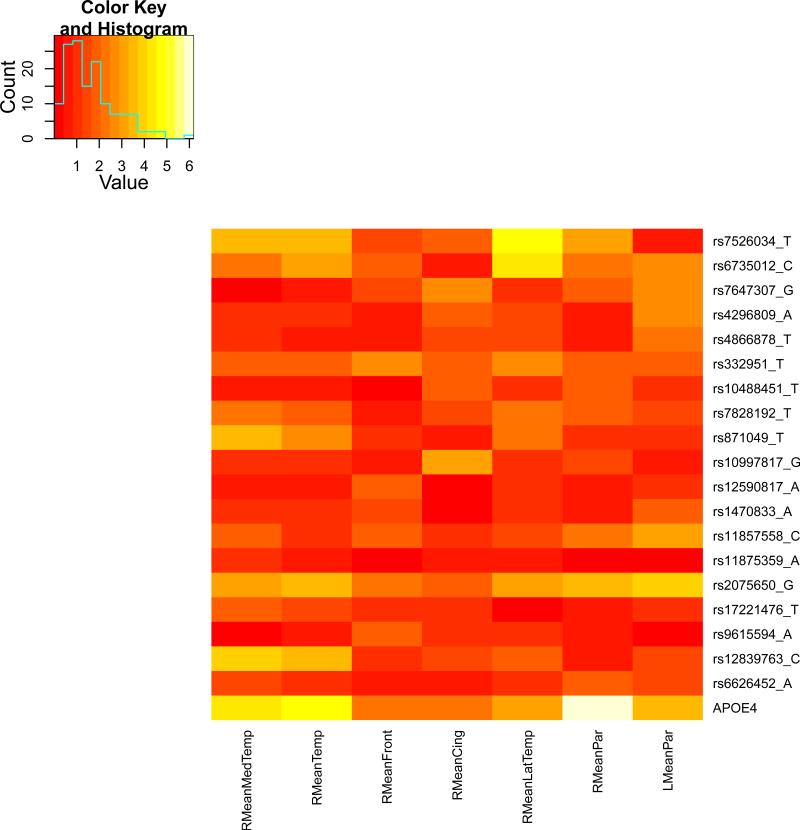
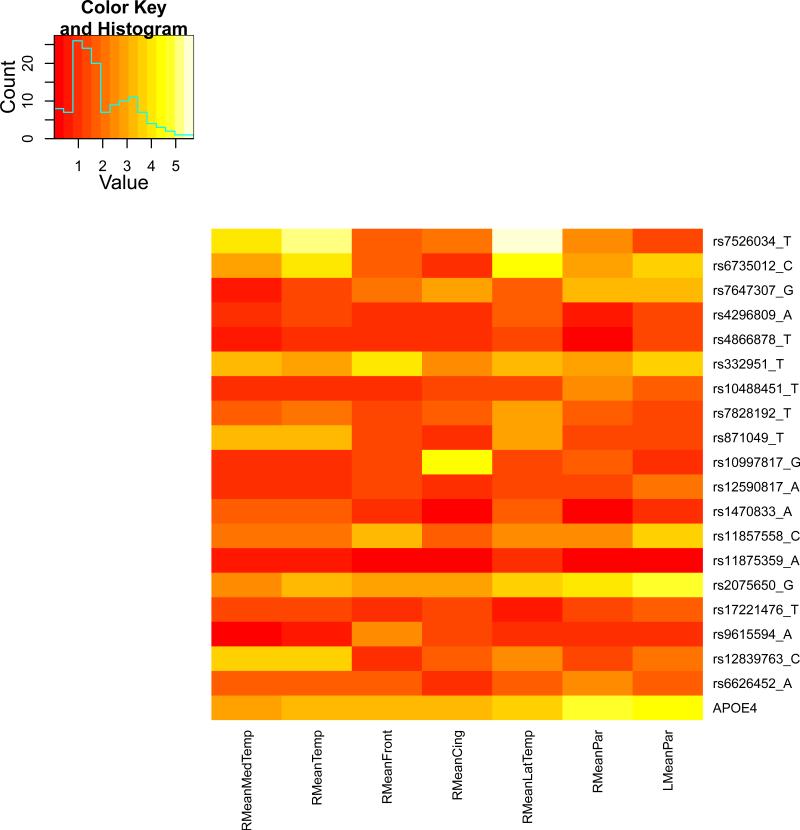
We present the heat maps of − log10 (p-values) of the new methods in Figure 1; as a comparison, the results from four existing methods are shown in Figure 2. In agreement with our theoretical analysis and simulation study, it is confirmed that i) the GEE-Score test, MANOVA and MultiPhen, ii) the GEE-UminP test and TATES, and iii) the GEE-SPU(1) test and the Averge method, yielded similar results. For this dataset, it turns out that the GEE-SPU(2), GEE-aSPU and GEE-aSPUw tests also gave p-values similar to each other, and to those of GEE-SPU(1). However, the three groups i)–iii) of the tests did give quite di erent results. Below, taking the GEE-Score, GEEUminP and GEE-SPU(1) as a representative for each group, we show their identified marginally significant SNPs at p-values < 10−6 and < 10−5 respectively. i) The GEE-Score test identified an association between rs429358 (in gene ApoE) and RMeanPar (MeanPar at the right side of the brain) with a p-value of 8.45 × 10−7; it also gave a p-value of 8.13 × 10−6 for rs7526034 and RMeanLatTemp. ii) the GEE-UminP test detected rs7526034 marginally associated with RMeanLatTemp and RMeanTemp with p-values of 3.10 × 10−6 and 7.90 × 10−6 respectively; note neither is significant at the level of p-value< 10−6. iii) the GEE-SPU(1) test identified rs7526034 to be associated with three traits, RMeanTemp, RMeanLatTemp and RMeanMedTemp, with p-values of 2.00×10−7, 6.00×10−7 and 9.00×10−7 respectively, in addition to a marginal association between rs12839763 and RMeanMedTemp with a p-value of 2.00 × 10−6. As a comparison, the GEE-aSPU test gave results similar to the GEE-SPU(1) test: for the above 4 associations indicated by the SPU(1) test, the aSPU test gave p-values of 6.00 × 10−7, 9.00 × 10−7, 1.80 × 10−6, and 4.20 × 10−6 respectively; in addition, it also gave a p-value of 9.00 × 10−6 to rs2075650 and LMeanPar. In summary, it appears that the three groups of the tests could identify di erent sets of (marginally) significant associations, though TATES and GEE-UminP did not identify any association with p-value < 10−6, illustrating a possible loss of power in taking out only most significant univariate associations.
Figure 1.
The heatmaps of − log10 (p-values) of the GEE-based tests for seven multivariate traits.
Figure 2.
The heatmaps of − log10 (p-values) of the four existing tests for seven multivariate traits
As in the simulation study, the p-values obtained from the Average method and SPU(1) were very close. However, because the former was based on the asymptotic Wald test while the latter was a Score test based on simulations, their p-values might be slightly di erent. For example, for association between rs2075650 and LMeanPar, the Average method gave a p-value of 9.94×10−6, which was essentially the same as 1.10×10−5 by the GEE-SPU(1) test.
The similar results between the Average method (or SPU(1)) and SPU(2) or aSPU test were presumably due to the relatively small numbers of univariate traits consisting of the seven multi-variate traits. To investigate the robustness of the tests to a larger number of traits, we pooled all seven multivariate traits together to form a combined trait; after removing duplicated ones, a total of 26 univariate traits remained. Since all the methods indicated marginal associations between the rs7526034 and/or rs429358 and several traits, we focused on the two SNPs. As shown in Table 15, in agreement with earlier analyses of the seven individual multivariate traits, i) for SNP rs429358, the GEE-Score test and MultiPhen gave the most significant p-values; ii) for SNP rs7526034, the GEE-SPU(2) and aSPU tests yielded most significant results, followed by those given by TATES and GEE-UminP. However, the Average method and GEE-SPU(1) gave much less significant results, suggesting their non-robustness to a large number of non-associated traits as confirmed in the simulation study. In summary, it seems that the GEE-Score test (or equivalently MultiPhen) and the GEE-aSPU test could give complementary and useful results.
Table 15.
P-values of testing on a pooled set of 26 univariate traits.
| GEE |
||||||||
|---|---|---|---|---|---|---|---|---|
| SNPs | Average | MultiPhen | TATES | UminP | Score | SPU(1) | SPU(2) | aSPU |
| rs7526034 | 1.40e-04 | 5.82e-04 | 1.72e-05 | 2.10e-05 | 5.86e-04 | 7.30e-05 | 7.00e-06 | 7.00e-06 |
| rs429358 | 1.42e-04 | 1.68e-05 | 1.23e-04 | 1.50e-04 | 2.32e-05 | 1.10e-04 | 7.00e-05 | 1.60e-04 |
To demonstrate the feasibility of the new tests for GWAS, we conducted a genome-wide scan with a set of 31 FreeSurfer traits. Since the results did not o er additional new insights, to save space, we report the results in Supplementary Materials.
4 Discussion
In this paper we have developed a class of the so-called SPU tests for association analysis of multiple (correlated) traits and a single SNP. We have also proposed an adaptive test called the aSPU test to estimate and thus select the most powerful SPU test for a given dataset. For multivariate trait-single SNP analysis, based on a marginal regression model in GEE that allows the SNP to have different effect sizes and e ect directions on different traits, the aSPU test can adapt to the existence and the number of the null (non-associated) traits e ectively. With a larger power parameter γ, the SPU(γ) test reduces the influence of null traits and reinforces the associated ones. Thus this test can maintain high power in the presence of a large number of null traits. This property is especially useful for studies where many correlated phenotypes are collected but there are no established guidelines to selecting relevant phenotypes. On the other hand, in the presence of many associated traits, the SPU(γ) test with a smaller γ will be more powerful. In particular, SPU(1) is quite similar to the Average (or Sum) method as used in Shen et al (2012), while SPU(2) is an extension of the SSU test for single trait-multilocus association analysis to multivariate trait-single locus analysis. As noted, under suitable conditions the SPU(2) test is the same as MDMR or KMR. We have also pointed out how some existing methods, like CCA/MANOVA, TATES and MultiPhen are related to the various GEE-based tests. We emphasize that, many of the existing methods, such as CCA/MANOVA and MultiPhen, may not be applicable to discrete traits or multiple loci, while our proposed GEE-Score and GEE-aSPU tests can with their general modeling and inference framework of GEE. Our proposed tests are potentially useful for a large number of traits, as arising as intermediate phenotypes in neuroimaging studies, which has not been adequately considered in the genetics literature. We also note that our proposed GEE-aSPU test can be equally applied to multiple principal components after PCA or PCH dimension reduction on a large number of traits, though further studies are needed.
From simulation studies we observed that the relative performance of the GEE-based Score and aSPU tests varied with the degree of the correlations among the traits and with the e ect sizes of the causal SNPs. When the traits were somewhat more weakly correlated (e.g. with an AR-1 correlation structure), regardless of the e ects size of the causal SNP, the aSPU test was much more powerful than the Score test and UminP test. However, under some situations, e.g. when the traits had a compound symmetry correlation structure, the aSPU test might not be as powerful as the Score test when the e ect sizes were small; the opposite conclusion held with larger e ect sizes. We note that, the aSPU test largely combines the strengths of the SPU(1) (equivalently the Average method), SPU(2) (closely related to MDMR and KMR), and SPU(∞) (similar to UminP and TATES), but differing from the Score test and MultiPhen while the latter two (and CCA/MANOVA) perform similarly. Since currently we do not have a simple guideline on how to choose between the aSPU and Score tests in practice, we recommend the use of both; we have also explored combining the two tests with some promising preliminary results (see Table 13), though more studies are needed.
We have focused on multitrait association testing on a single SNP. A natural extenstion is to multitrait-multiple SNP testing. For univariate trait analysis, it has been established that testing on multiple SNPs simultaneously may gain power (Pan 2009), especially for RVs as evidenced by the increasing use of the burden tests and variance component tests (Basu and Pan 2011). Pan et al (2014) have proposed and studied an analogous aSPU test for RVs, which data-adaptively over-weights (unknown and estimated) associated RVs (while down-weighting non-associated RVs). In contrast, here our proposed aSPU test adaptively over-weights (unknown and estimated) associated traits (while down-weighting non-associated traits). It would be interesting to see whether combining the two ideas would work for multitrait-multiple SNP association testing, especially in the presence of large numbers of traits and of SNPs. An advantage of the aSPU test is its weighting on, rather than directly selecting, traits (or SNPs), in order to alleviate the e ects of non-associated traits (or SNPs) on diminishing the power of a test, expected to be present with many traits (or SNPs); given small e ect sizes of common variants (or small MAFs of RVs), weighting tends to outperform selection.
It seems to be a common belief that accounting for correlations among multiple traits would automatically increase power, which however may not be true, or at least not as simple as it may sound. Here are our arguments. First, using a non-independent working correlation matrix Rw ≠ I in GEE can be regarded as an attempt to account for correlations among multiple traits; however, as shown in Tables 1 and 12, in these situations a test may or may not have improved power. In particular, the GEE Score test is invariant to the use of the working correlation matrix (with an equal cluster size). Second, as directly shown numerically here (e.g. Table 9), the GEE-SPU(2) test could be more powerful than the GEE Score test, though the SPU(2) test statistic ignores the correlations among the components of the score vector (due to the correlations among the traits) while the Score test statistic does not. The same phenomenon is also observed in single trait-multiple SNP analysis (Pan 2009), in which the SSU test (or equivalently KMR) is known to be often, but not always, more powerful than the Score test. Pan (2009) offers an explanation based on a test's rejection region, which however is hard to visualize for high-dimensional testing while the power also depends on some unknown association parameters. Certainly this is a topic worth further investigation.
Finally, we have not compared our methods with those based on constructing latent composite traits such as PCA and PCH; a particularly interesting topic is to investigate how our proposed tests compare with the modified PCH method of Lin et al (2012) for high-dimensional neuroimaging traits.
Supplementary Material
Table 4.
Empirical power when the multiple traits were correlated with a CS structure with correlation coefficient r; the first five traits were associated with a causal SNP with log-ORs βj ~ U(0.8, 1), while all others had βj = 0. An independence working correlation structure was used in GEE.
| GEE |
||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MDMR |
SPU(γ) |
|||||||||||||||||
| r | SNP | #trait | Average | MultiPhen | TATES | L 1 | L 2 | MANOVA | Score | UminP | γ = 1 | 2 | 3 | 4 | 5 | 6 | ∞ | aSPU |
| 0.3 | 2 | 5 | 0.888 | 0.683 | 0.823 | 0.878 | 0.883 | 0.683 | 0.682 | 0.815 | 0.889 | 0.880 | 0.868 | 0.862 | 0.851 | 0.843 | 0.812 | 0.865 |
| 10 | 0.567 | 0.685 | 0.727 | 0.786 | 0.826 | 0.686 | 0.684 | 0.708 | 0.567 | 0.830 | 0.777 | 0.819 | 0.796 | 0.807 | 0.772 | 0.795 | ||
| 20 | 0.218 | 0.613 | 0.665 | 0.616 | 0.729 | 0.615 | 0.611 | 0.657 | 0.223 | 0.724 | 0.667 | 0.787 | 0.756 | 0.792 | 0.762 | 0.757 | ||
| 30 | 0.116 | 0.528 | 0.607 | 0.435 | 0.574 | 0.531 | 0.528 | 0.591 | 0.117 | 0.577 | 0.541 | 0.725 | 0.695 | 0.742 | 0.738 | 0.703 | ||
| 40 | 0.084 | 0.424 | 0.536 | 0.262 | 0.442 | 0.435 | 0.424 | 0.534 | 0.084 | 0.432 | 0.445 | 0.644 | 0.609 | 0.680 | 0.678 | 0.639 | ||
| 0.3 | 3 | 5 | 0.334 | 0.178 | 0.292 | 0.328 | 0.330 | 0.178 | 0.177 | 0.281 | 0.331 | 0.327 | 0.321 | 0.315 | 0.312 | 0.305 | 0.289 | 0.320 |
| 10 | 0.184 | 0.167 | 0.203 | 0.240 | 0.269 | 0.167 | 0.167 | 0.197 | 0.182 | 0.273 | 0.260 | 0.282 | 0.267 | 0.273 | 0.244 | 0.249 | ||
| 20 | 0.092 | 0.138 | 0.179 | 0.149 | 0.189 | 0.141 | 0.137 | 0.173 | 0.090 | 0.188 | 0.191 | 0.242 | 0.246 | 0.257 | 0.242 | 0.229 | ||
| 30 | 0.074 | 0.121 | 0.143 | 0.107 | 0.120 | 0.127 | 0.119 | 0.146 | 0.079 | 0.128 | 0.141 | 0.185 | 0.184 | 0.203 | 0.204 | 0.181 | ||
| 40 | 0.058 | 0.105 | 0.132 | 0.088 | 0.113 | 0.109 | 0.104 | 0.134 | 0.062 | 0.112 | 0.118 | 0.161 | 0.168 | 0.179 | 0.188 | 0.168 | ||
| 0.5 | 2 | 5 | 0.829 | 0.602 | 0.784 | 0.821 | 0.822 | 0.604 | 0.601 | 0.763 | 0.832 | 0.821 | 0.811 | 0.806 | 0.800 | 0.793 | 0.769 | 0.806 |
| 10 | 0.424 | 0.725 | 0.694 | 0.629 | 0.729 | 0.728 | 0.725 | 0.685 | 0.430 | 0.734 | 0.714 | 0.766 | 0.750 | 0.765 | 0.737 | 0.723 | ||
| 20 | 0.163 | 0.665 | 0.624 | 0.344 | 0.524 | 0.666 | 0.662 | 0.634 | 0.161 | 0.534 | 0.567 | 0.697 | 0.695 | 0.725 | 0.722 | 0.694 | ||
| 30 | 0.093 | 0.570 | 0.549 | 0.186 | 0.318 | 0.577 | 0.570 | 0.570 | 0.093 | 0.319 | 0.440 | 0.593 | 0.609 | 0.666 | 0.707 | 0.653 | ||
| 40 | 0.067 | 0.484 | 0.487 | 0.119 | 0.203 | 0.496 | 0.483 | 0.508 | 0.072 | 0.202 | 0.333 | 0.518 | 0.544 | 0.612 | 0.654 | 0.613 | ||
| 0.5 | 3 | 5 | 0.291 | 0.149 | 0.270 | 0.288 | 0.290 | 0.150 | 0.148 | 0.259 | 0.290 | 0.294 | 0.293 | 0.285 | 0.284 | 0.279 | 0.263 | 0.287 |
| 10 | 0.129 | 0.181 | 0.209 | 0.171 | 0.207 | 0.182 | 0.180 | 0.201 | 0.126 | 0.203 | 0.223 | 0.245 | 0.249 | 0.255 | 0.245 | 0.223 | ||
| 20 | 0.077 | 0.138 | 0.160 | 0.098 | 0.130 | 0.139 | 0.136 | 0.168 | 0.075 | 0.131 | 0.158 | 0.196 | 0.212 | 0.220 | 0.228 | 0.205 | ||
| 30 | 0.067 | 0.117 | 0.129 | 0.077 | 0.092 | 0.121 | 0.117 | 0.139 | 0.065 | 0.091 | 0.118 | 0.144 | 0.156 | 0.166 | 0.195 | 0.181 | ||
| 40 | 0.055 | 0.110 | 0.113 | 0.071 | 0.078 | 0.116 | 0.109 | 0.129 | 0.054 | 0.079 | 0.105 | 0.134 | 0.148 | 0.163 | 0.190 | 0.166 | ||
Acknowledgment
This research was supported by NIH grants R01HL65462, R01HL105397, R01HL116720 and R01GM081535. The authors are grateful to the three reviewers for many helpful and constructive comments.
Data collection and sharing for this project was funded by the Alzheimer's Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: Alzheimer's Association; Alzheimer's Drug Discovery Foundation; BioClinica, Inc.; Biogen Idec Inc.; Bristol-Myers Squibb Company; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; F. Ho mann-La Roche Ltd and its a liated company Genentech, Inc.; GE Healthcare; Innogenetics, N.V.; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Medpace, Inc.; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Synarc Inc.; and Takeda Pharmaceutical Company. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer's Disease Cooperative Study at the University of California, San Diego. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of California, Los Angeles. This research was also supported by NIH grants P30 AG010129 and K01 AG030514.
A Appendix: Relationships Between the New and Existing Tests
A.1 The Average (or Sum) test and the GEE-SPU(1) test
A simple dimension reduction method is to take the average (or sum) of the multiple traits and use it as a single trait to assess its association with a single SNP; we call the corresponding method as the Average or Sum method (Shen et al 2011; van der Sluis et al 2013). It is easy to see that the score vectors of the two methods in linear regression (or any GLM with a canonical link) are equivalent to each other (up to a constant) as
which is equal to the SPU(1) test statistic under Rw = I in GEE. Hence, the Score test version of the Average or Sum test and GEE-SPU(1) tests (under Rw = I) are exactly the same. We implemented the Average test as a Wald test and used its asymptotic distribution to calculate its p-values while we used simulations to calculated the p-values for GEE-SPU(1), which led to some minor di erences in their results.
A.2 TATES, GEE-UminP, GEE-SPUw(∞) and GEE-SPU(∞) tests
It is easy to verify that the GEE-UminP and GEE-SPUw(∞) tests are exactly the same. It is noted that, under the working independence model, the GEE score vector and its covariance estimate are exactly the same as that for univariate analyses on each of the multiple traits separately. Hence, the GEE-UminP and GEE-SPUw(∞) tests are also closely related to univariate analysis-based TATES (van der Sluis et al 2013), but di er in two aspects: first, TATES uses Simes procedure for multiple testing adjustment, while the former two use an “exact” method for such a purpose; second, TATES uses a correlation matrix input by the user to estimate the null distribution of the test statistic, hence is computationally simpler but may be less accurate.
A.3 CCA, MANOVA and the GEE-Score test
To test for association between multiple traits and a single SNP (without any other covariates), CCA and MANOVA are equivalent (Ferreira and Purcell 2009; Yang and Wang 2012). They are based on the largest eigen-value ρ2 of
where , and are sample variance-covariance matrices. In the current context with a single SNP xi, since B is a scalar, we have ρ2 = B.
With a working independence model Rw = I, the GEE-Score test statistic is
in which the second equality holds because SXX is a scalar. Furthermore, as shown earlier, the GEE-Score test is invariant to Rw in the current context. Hence CCA and MANOVA are equivalent to the GEE-Score test, regardless of the working correlation matrix Rw being used in GEE.
A.4 MDMR, MANOVA and the GEE-SPU(2) test
MDMR is a nonparametric method as a generalization of Fisher's MANOVA (McArdle and Anderson 2001); it has been applied to detect association between a single trait and multiple SNPs, named as genomic distance-based regression (GDBR) (Wessel and Schork 2006). Schork and colleagues have outlined its application to analysis of longitudinal or multivariate traits (Zapala and Schork 2012). We briefly summarize its main steps as the following:
Step 1. Calculate an n × n distance matrix for all pairs of subjec ts by D = (Dij) with Dij = d(Yi, Yj) and d(, ) being a distance or semi-distance metric.
Step 2. Calculate A = (−Dij2/2).
Step 3. Obtain a centered similarity matrix G = (I − 11′/n)A(I − 11′/n), where 1 is an n × 1 vector of all 1's;
Step 4. Denote X as the n × 1 vector of centered genotype scores with elements xi (and ).
Step 5. Calculate the projection matrix H = X(X′X)−1X′;
- Step 6. Calculate a pseudo F-statistic as
where tr(A) is the trace of matrix A.(8)
To obtain a p-value, we recourse to permutations by shu ing X (or, equivalently, shuffling both the rows and columns of A simultaneously).
As discussed by McArdle and Anderson (2001), if G is an outer product matrix, say G = ZZ′ with an n × k matrix Z, the above F-test is simply testing H0′ : B = 0 in a multivariate linear model
| (9) |
where 1 is an n × 1 vector of all 1's, μ is a 1 × p vector of unknown intercepts, B is a 1 × p vector of unknown regression coe cients, and ∈ is an n × p matrix of random errors. Following the same argument in Pan (2011), it can be shown that
| (10) |
which is the same as the GEE-SPU(2) test statistic for the multivariate linear model (9) under the working independence model. In particular, if the Euclidean distance (i.e. L2-norm) is used as the distance metric d(, ), we have Z = Y ; thus, MDMR(L2), the MDMR implementation with the Euclidean distance, is the same as the GEE-SPU(2) test. Importantly, as to be shown, GEE-SPU(2) loses power in the presence of many null traits, so does MDMR.
Furthermore, MANOVA is based on the same model (9) with Z = Y ; however, the (approximate) F statistics in MANOVA are di erent from (8). For example, the Wilks statistic is based on
with |B| as the determinant of B. For this reason, MANOVA and MDMR(L2) will not be the same.
A.5 KMR and the GEE-SPU(2) test
KMR has been extended to multivariate quantitative traits (Maity et al 2012; Schifano et al 2012; Wang et al 2013). In the current setting, its test statistic is
where V0 = Var(Y|H0) and K is a kernel function. With a single SNP, it su ces to use a linear kernel with K = XX′, thus TKMR is the same as the GEE-SPU(2) test statistic if the working correlation Rw is the true correlation structure of Yi (i.e. Rw = Corr(Yi|H0)).
Since the extended KMR method is based on a mixed-effects model, it is not surprising to see that it requires specifying the correct correlation structure; in contrast, our proposed GEESPU(2) and other SPU tests only need a working, not necessarily correct, correlation structure Rw, maintaining the main advantage of the GEE methodology (while possessing its disadvantage of possible e ciency loss). Furthermore, it is not clear how to extend KMR to multiple discrete (e.g. binary) traits, while our GEE-SPU tests can be easily extended to other types of traits (as long as they can be modeled by GLMs). More importantly, as to be shown, GEE-SPU(2) loses power in the presence of many null traits, suggesting the same drawback of KMR.
A.6 MultiPhen and the GEE-Score test
MultiPhen (O'Reilly et al., 2012) is based on fitting a proportional odds model (POM). For simplicity, here we assume that xi's are not centered or transformed; otherwise, we just need to modify some notation accordingly. Define πj(y) = Pr(xi = j|Yi = y), and for j = 0, 1 and 2. The POM is
| (11) |
for j = 0 and 1. To test H0: β = (β1, ..., βk)′ = 0, MultiPhen applies a likelihood ratio test. We can equally apply an asymptotically equivalent Score test. Following McCullagh (1980), after some algebra, we derive the negative score vector for the POM as
| (12) |
where for j = 0, 1 and 2. In contrast, the Score vector for the GEE working independence model (4) can be written as
| (13) |
Comparing the two score vectors UPOM and UGEE, we see that they only differ in their weights on Yi's for xi = 0 and xi = 2. Hence, we would expect that MultiPhen and GEE-Score test give similar results unless the MAF of xi is extreme. The similarity of empirical performance between MultiPhen and MANOVA was observed by other authors (e.g. van der Sluis et al 2013), which is shown theoretically here, based on our earlier result on the equivalence between MANOVA and the GEE-Score test.
A.7 Generalized Kendall's tau and the GEE-Score test
Zhang et al (2010) proposed a nonparametric method to test association between multiple traits and a single SNP. The test statistic is a U-statistic as a generalized Kendall's tau (denoted as GKτ). Specifically, define uij = (f(Yi1 − Yj1), ..., f(Yiq − Yjq))′, where f() is an identity function for quantitative traits or binary traits, or a sign function for ordinal traits; in the former case, we have uij = Yi − Yj. Define . Then the GKτ statistic, after ignoring a constant factor, 2/(n − 1), is , which is asymptotically distributed as N(0, V0) under H0. The corresponding GKτ test is a score or Wald-type test: under H0. With quantitative or binary traits, it is easy to verify ; under this condition we have exactly τ = U if a canonical link function and a working independence model are used in GEE, suggesting the equivalence between the GKτ test and the GEE Score test with Rw = I, which was confirmed by our numerical results (not shown). It is interesting to note that the nonparametric GKτ test coincides with our semi-parametric GEE approach.
This equivalence suggests a natural extension of the GKτ test to multiple SNPs (or markers): a new GKτ test statistic can be defined as the same as the score vector U for multiple SNPs in GEE with a canonical link function and a working independence model. This extension overcomes a conceptual di culty in generalizing Kendall's tau to two random vectors with unequal lengths. Furthermore, rather than using a score- or Wald-type test (which may be low-powered with a high dimensionality of kq), we can explore the power of the aSPU test as discussed before. Finally, our proposed approach di ers from the GKτ test in the case with covariates. The modified GKτ test with covariates (Zhu et al 2012) uses a weighting scheme to adjust for covariate effects, in contrast to our regression approach.
Reference
- Aschard H, Vilhjalmsson B, Wu C, Greliche N, Morange PE, Wolpin B, Tregouet DA, Kraft P. Maximizing the power in Principal Components Analysis of Correlated Phenotypes. 2013 doi: 10.1016/j.ajhg.2014.03.016. arXiv:1309.2978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basu S, Pan W. Comparison of statistical tests for disease association with rare variants. Genetic Epidemiology. 2011;35:606–619. doi: 10.1002/gepi.20609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai T, Liu W, Xia Y. Two-sample test of high dimensional means under dependence. To appear in Journal of the Royal Statistical Society B. 2013 [Google Scholar]
- Chen M-H, Liu X, Wei F, Larson MG, Fox CS, Vasan RS, Yang Q. A comparison of strategies for analyzing dichotomous outcomes in genome-wide association studies with general pedigrees. Genetic Epidemiology. 2011;35:650–657. doi: 10.1002/gepi.20614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole DA, Maxwell SE, Arvey R, Salas E. How the power of MANOVA can both increase and decrease as a function of the intercorrelations among the dependent variables. Psychological Bulletin. 1984;115:465–474. [Google Scholar]
- Ferreira MA, Purcell SM. A multivariate test of association. Bioinformatics. 2009;25:132–133. doi: 10.1093/bioinformatics/btn563. [DOI] [PubMed] [Google Scholar]
- Fitzmaurice G, Laird N. A likelihood-based method for analyzing longitudinal binary responses. Biometrika. 1993;80:141–151. [Google Scholar]
- Glahn DC, Paus T, Thompson PM. Imaging genomics: mapping the influence of genetics on brain structure and function. Human Brain Mapping. 2007;28:461–463. doi: 10.1002/hbm.20416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo X, Pan W, Connett JE, Hannan PJ, French SA. Small-sample performance of the robust score test and its modifications in generalized estimating equations. Statistics in Medicine. 2005;24:3479–3495. doi: 10.1002/sim.2161. [DOI] [PubMed] [Google Scholar]
- Han F, Pan W. A data-adaptive sum test for disease association with multiple common or rare variants. Human Heredity. 2010;70:42–54. doi: 10.1159/000288704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartig M, Truran-Sacrey D, Raptentsetsang S, Simonson A, Schu N, Weiner M. UCSF FreeSurfer. Methods. Rev. 2012 Dec;11:2012. [Google Scholar]
- Klei L, Luca D, Devlin B, Roeder K. Pleiotropy and principal components of heritability combine to increase power for association analysis. Genet Epidemiol. 2008;32:9–19. doi: 10.1002/gepi.20257. [DOI] [PubMed] [Google Scholar]
- Korte A, Vilhjálmsson BJ, Segura V, Platt A, Long Q, Nordborg M. A mixed-model approach for genome-wide association studies of correlated traits in structured populations. Nature Genetics. 2012;44:1066–1071. doi: 10.1038/ng.2376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lan H, Stoehr J, Nadler S, Schueler K, Yandell B, Attie A. Dimension reduction for mapping mRNA abundance as quantitative traits. Genetics. 2003;164:1607–1614. doi: 10.1093/genetics/164.4.1607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lange C, Silverman E, Xu X, Weiss S, Laird N. A multivariate family-based association test using generalized estimating equations: FBAT-GEE. Biostatistics. 2003;4:195–206. doi: 10.1093/biostatistics/4.2.195. [DOI] [PubMed] [Google Scholar]
- Li X, Basu S, Miller MB, Iacono WG, McGue M. A Rapid Generalized Least Squares Model for a Genome-Wide Quantitative Trait Association Analysis in Families. Human Heredity. 2011;71:67–82. doi: 10.1159/000324839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang K, Zeger S. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73:13–22. [Google Scholar]
- Lin DY. An e cient Monte Carlo approach to assessing statistical significance in genomic studies. Bioinformatics. 2005;21:781–787. doi: 10.1093/bioinformatics/bti053. [DOI] [PubMed] [Google Scholar]
- Lin DY, Tang ZZ. A general framework for detecting disease associations with rare variants in sequencing studies. Am J Hum Genet. 2011;89:354–367. doi: 10.1016/j.ajhg.2011.07.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin J, Zhu HT, Knickmeyer R, Styner M, Gilmore JH, Ibrahim JG. Projection Regression Models for Multivariate Imaging Phenotype. Genetic Epidemiology. 2012;36:631–641. doi: 10.1002/gepi.21658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Pei Y, Papasian C, Deng H. Bivariate association analyses for the mixture of continuous and binary traits with the use of extended generalized estimating equations. Genetic Epidemiology. 2009;33:217–227. doi: 10.1002/gepi.20372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maity A, Sullivan PF, Tzeng JY. Multivariate phenotype association analysis by marker-set kernel machine regression. Genet Epidemiol. 2012;36:686–695. doi: 10.1002/gepi.21663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McArdle BH, Anderson MJ. Fitting multivariate models to community data: A comment on distance-based redundancy analysis. Ecology. 2001;82:290–297. [Google Scholar]
- McCullagh P. Regression models for ordinal data (with discussion). J. R. Stat. Soc. B. 1980;42:109–142. [Google Scholar]
- McCullagh P, Nelder JA. Generalized linear models. Chapman and Hall; London: 1983. [Google Scholar]
- O'Reilly PF, Hoggart CJ, Pomyen Y, Calboli FC, Elliott P, Jarvelin M-R, Coin LJ. MultiPhen: joint model of multiple phenotypes can increase discovery in GWAS. PLoS One. 2012;7:e34861. doi: 10.1371/journal.pone.0034861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan W. On the Robust Variance Estimator in Generalised Estimating Equations. Biometrika. 2001;88:901–906. [Google Scholar]
- Pan W. Asymptotic tests of association with multiple SNPs in linkage disequilibrium. Genetic Epidemiology. 2009;33:497–507. doi: 10.1002/gepi.20402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan W. Relationship between genomic distance-based regression and kernel machine regression for multi-marker association testing. Genet Epidemiol. 2011;35:211–216. doi: 10.1002/gepi.20567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan W, Wei P, Zhang Y, Shen X. Technical Report 2014-001, Division of Biostatistics. School of Public Health, University of Minnesota; 2014. A powerful and adaptive association test for rare variants. Available online at http://cpheo2.sph.umn.edu/sphwp/facstaff/image/techreport/rr2014-001.pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schifano ED, Epstein MP, Bielak LF, Jhun MA, Kardia SL, Peyser PA, Lin X. SNP Set Association Analysis for Familial Data. Genet Epidemiol. 2012;36:797–810. doi: 10.1002/gepi.21676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seaman SR, Mller-Myhsok B. Rapid simulation of Pvalues for product methods and multiple-testing adjustment in association studies. Am J Hum Genet. 2005;76:399–408. doi: 10.1086/428140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen L, Kim S, Risacher SL, Nho K, Swaminathan S, West JD, Foroud T, Pankratz N, Moore JH, Sloan CD, et al. Whole genome association study of brain-wide imaging phenotypes for identifying quantitative trait loci in MCI and AD: a study of the ADNI cohort. Neuroimage. 2010;53:1051–1063. doi: 10.1016/j.neuroimage.2010.01.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang CS, Ferreira MA. A gene-based test of association using canonical correlation analysis. Bioinformatics. 2012;28:845–850. doi: 10.1093/bioinformatics/bts051. [DOI] [PubMed] [Google Scholar]
- van der Sluis S, Posthuma D, Dolan CV. TATES: E cient Multivariate Genotype-Phenotype Analysis for Genome-Wide Association Studies. PLoS Genet. 2013;9:e1003235. doi: 10.1371/journal.pgen.1003235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang K, Abbott D. A principal components regression approach to multilocus genetic association studies. Genetic Epidemiology. 2007;32:108–118. doi: 10.1002/gepi.20266. [DOI] [PubMed] [Google Scholar]
- Wang X, Kammerer CM, Anderson S, Lu J, Feingold E. A comparison of principal component analysis and factor analysis strategies for uncovering pleiotropic factors. Genetic Epidemiology. 2008;33:325–331. doi: 10.1002/gepi.20384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Morris NJ, Zhu X, Elston RC. A variance component based multi-marker association test using family and unrelated data. BMC Genetics. 2013;14:17. doi: 10.1186/1471-2156-14-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu M, Lee S, Cai T, Li Y, Boehnke M, Lin X. Rare-variant association testing for sequencing data with the sequence kernel association test. American Journal of Human Genetics. 2011;89:82–93. doi: 10.1016/j.ajhg.2011.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Q, Wu H, Guo C-Y, Fox CS. Analyze multivariate phenotypes in genetic association studies by combining univariate association tests. Genetic Epidemiology. 2010;34:444–454. doi: 10.1002/gepi.20497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Q, Wang Y. Methods for analyzing multivariate phenotypes in genetic association studies. Journal of Probability and Statistics. 2012;2012:652569. doi: 10.1155/2012/652569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zapala MA, Schork NJ. Statistical properties of multivariate distance matrix regression for high-dimensional data analysis. Front. Genet. 2012;3:190. doi: 10.3389/fgene.2012.00190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu W, Zhang H. Why do we test multiple traits in genetic association studies? J. Korean Stat. Soc. 2009;38:1–10. doi: 10.1016/j.jkss.2008.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Liu C-T, Wang X. An association test for multiple traits based on the generalized Kendall's tau. J. Am. Stat. Assoc. 2010;105:473–481. doi: 10.1198/jasa.2009.ap08387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu W, Jiang Y, Zhang H. Nonparametric Covariate-Adjusted Association Tests Based on the Generalized Kendall's Tau. J. Am. Stat. Assoc. 2012;107:1–11. doi: 10.1080/01621459.2011.643707. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.