Figure 1. Second moments of particle distributions and mean square displacements obtained from a simulation of freely diffusing particles.

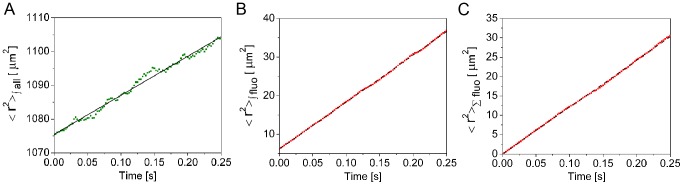
The data for this figure (shown in green and red) comes from the simulation of Video 0.1 which corresponds to a system of particles that diffuse with 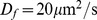in the absence of binding sites. The simulation starts with an equilibrium situation that is perturbed by adding 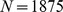fluorescent particles to the the central 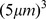cube of the 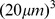simulation volume. In this figure we characterize the rate at which the deviations with respect to equilibrium of the concentrations of all particles and of the added ones spread out with time by means of second moments. We compare these second moments with the MSD of the added particles. Please notice that we are not plotting the mean square displacements in A) and B) but a quantity (the second moment) that depends linearly with the time lag with the same slope as the mean square displacement. For more details see Materials and Methods. A: 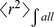(shown in green) computed using Eq. (12) with 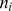the number of all particles in the 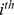box. Linear fit (shown in black). B: 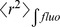(shown in red) computed using Eq. (12) with 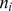the number of fluorescent particles in the 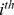box. Linear fit (shown in black). C: The mean of the squared displacements of the added particles (shown in red) computed using Eq. (11). Linear fit (shown in black). As explained in supplementary text S3 the diffusion coefficient, 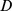, can be estimated by taking 1/6 of the slope of the fitting curves. In this case the three estimates yield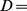 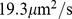(A), 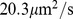(B) and 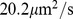(C). The second moment shown in A) corresponds to the "collective diffusion coefficient'', the one in C) to the "single molecule diffusion coefficient'' and the one in B) could be called 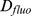. According to the theory all three should coincide in the case of freely diffusing particles and this is reflected in this figure.