Abstract
Objective
Chronic Fatigue (CF) still remains unclear about its etiology, pathophysiology, nomenclature and diagnostic criteria in the medical community. Traditional Chinese medicine (TCM) adopts a unique diagnostic method, namely ‘bian zheng lun zhi’ or syndrome differentiation, to diagnose the CF with a set of syndrome factors, which can be regarded as the Multi-Label Learning (MLL) problem in the machine learning literature. To obtain an effective and reliable diagnostic tool, we use Conformal Predictor (CP), Random Forest (RF) and Problem Transformation method (PT) for the syndrome differentiation of CF.
Methods and Materials
In this work, using PT method, CP-RF is extended to handle MLL problem. CP-RF applies RF to measure the confidence level (p-value) of each label being the true label, and then selects multiple labels whose p-values are larger than the pre-defined significance level as the region prediction. In this paper, we compare the proposed CP-RF with typical CP-NBC(Naïve Bayes Classifier), CP-KNN(K-Nearest Neighbors) and ML-KNN on CF dataset, which consists of 736 cases. Specifically, 95 symptoms are used to identify CF, and four syndrome factors are employed in the syndrome differentiation, including ‘spleen deficiency’, ‘heart deficiency’, ‘liver stagnation’ and ‘qi deficiency’.
The Results
CP-RF demonstrates an outstanding performance beyond CP-NBC, CP-KNN and ML-KNN under the general metrics of subset accuracy, hamming loss, one-error, coverage, ranking loss and average precision. Furthermore, the performance of CP-RF remains steady at the large scale of confidence levels from 80% to 100%, which indicates its robustness to the threshold determination. In addition, the confidence evaluation provided by CP is valid and well-calibrated.
Conclusion
CP-RF not only offers outstanding performance but also provides valid confidence evaluation for the CF syndrome differentiation. It would be well applicable to TCM practitioners and facilitate the utilities of objective, effective and reliable computer-based diagnosis tool.
Background
Chronic Fatigue (CF) is a sub-health status, pathologically characterized by nonspecific extreme fatigue (including physical fatigue and mental fatigue) over six months [1]. In the past, CF is a widespread illness which prevails among the people who lives under a fast-paced and stressful life. Thus far, the etiology, pathophysiology, nomenclature and diagnostic criteria of CF are still underexplored in Western medicine [2], [3]. Alternatively, Traditional Chinese Medicine (TCM) has provided an effective approach for personalized diagnosis and treatment of CF, and has paid increasing attention as a complementary medicine by the medical researchers [4], [5]. Unfortunately, TCM diagnosis still causes skepticism and criticism because TCM practitioners diagnose the patient only based on their subjective observation, knowledge, and clinical experience, which lacks objective test and cannot be scientifically proven by clinical trials [6]. Under the circumstances, it is desired to establish an objective and standardized diagnosis system for CF in TCM. Recently, researchers have found that machine learning technologies are able to figure out the inherent mechanism of TCM diagnosis and provide corrective predictions for patients [7], [8]. Therefore, a computer-aided system aiming at providing objective and reliable diagnosis is highly desired for the better understanding of the TCM diagnosis of chronic fatigue.
Differing from the western medicine, TCM adopts a unique diagnostic method, namely ‘bian zheng lun zhi’ or syndrome differentiation [9]–[11], to practically diagnose the CF. According to the theory of TCM, the syndrome or zheng is a comprehensive description of the pathology of a disease in the body. Actually, the syndrome consists of a set of syndrome factors. Each factor is defined in terms of the location and condition of the body. The term location in TCM is similar to that of the Western medicine, such as heart, liver, spleen, lung, kidney and stomach. However, the term condition in TCM is totally different from the Western medicine, which reflects the disharmony in the body, such as the deficiency or excess of qi, blood, yin and yang. In the viewpoint of TCM, the body struggles to maintain a dynamic equilibrium between its internal conditions and the external environment. Several syndrome factors of the body will express simultaneously when a pathogenic disease occurs. In general, the total number of syndrome factors in TCM is about 60, and the related syndrome factors for a particular disease is a subset of all of the syndrome factors [12]–[14]. For example, the syndrome factors that applied for CF include ‘spleen deficiency’, ‘heart deficiency’, ‘liver stagnation’ and ‘qi deficiency’. When faced with a patient, TCM practitioners should first execute the manipulations of ‘inspection’, ‘auscultation-olfaction’, ‘interrogation’ and ‘palpation’ to identify the symptoms, and then diagnose which syndrome factors have expressed simultaneously and select them to be the diagnostic output for CF. Consequently, a corresponding TCM treatment is proposed based on these diagnosis results.
The above TCM diagnostic process can be seen as a pattern recognition process. The symptoms in TCM correspond to features in the machine learning literature, and syndrome factors serve as classes or labels. In this sense, the particular syndrome differentiation that diagnoses disease by a set of syndrome factors falls into the Multi-Label Learning (MLL) in the machine learning literature [15], [16]. Therefore, it is appropriate to design an MLL model for the diagnosis of chronic fatigue in TCM.
MLL technique addresses the learning setting where an instance is designated by a set of labels [17]–[19]. Accordingly, the MLL classifier would learn a discriminative function to output the region prediction (a set of labels) for the testing instance, which is different with the point prediction by traditional classifier. Further, the learning function can be regarded as the confidence measurement which measures the confidence of each label to be the true label or not. Given a pre-defined threshold, the irrelevant labels can be removed and the remaining ones are used to construct the region prediction [20]. Though MLL methods have been applied in various domains, such as image processing, text analysis and speech recognition, there are limited amount of research that applied to the syndrome differentiation in TCM. In the literature, a representative work is the application of ML-KNN (K-Nearest Neighbor) algorithm, which aims to diagnose the syndrome differentiation of coronary heart disease (based on 6 syndrome factors) [21], [22]. They computed the posterior probability of each label as the confidence measurement and selected those labels whose posterior probability is larger than a pre-defined threshold to construct the region prediction. The experiments have shown a promising performance for the syndrome differentiation.
Nevertheless, the reliability of the prediction result in the MLL framework has not been well studied, which is of crucial importance to the application of the high-risk medical diagnosis. That is, the reliable results are very important for the clinical treatment practically. As for the predictions of MLL model, it would be highly beneficial if the MLL model could provide a reliable analysis for the expert practitioners and patients. In general, the ML-KNN approach constructs the posterior probability as the confidence measurement for each label, provided that the proper prior assumption of the dataset distribution can be obtained [23]. However, it is impossible to properly figure out the prior knowledge about the dataset distribution because the TCM datasets are of high-dimensional and nonlinear patterns. Accordingly, the posterior probability always cannot provide valid confidence measurement for MLL prediction.
Motivated by the above observation, in this paper, we use Conformal Predictor (CP) and Random Forest (RF) to enhance the MLL framework, which aims to not only offer outstanding performance but also provide valid confidence for the syndrome differentiation of CF in TCM. CP is a recently development in the machine learning literature, which is virtually a confidence machine that tails its prediction with a valid confidence evaluation [24]. It has been proven that CP is calibrated in online learning, i.e. the accuracy of CP prediction can be hedged by the confidence level. In the past, CP has demonstrated the reliability on its prediction in many high-risk applications, such as medical diagnosis, fault detection and finance analysis [25]–[27]. CP outputs region prediction rather than point prediction, which makes it competent for the multi-label recognition. Meanwhile, RF is a powerful machine learning algorithm which can deal with dataset suffering heavily from high-dimensional, noisy, with missing-values, categorical and highly correlated features [28]. In this sense, RF is competent for TCM dataset where the descriptions of the symptom(features) always take categorical or qualitative values [29], [30]. Thus, CP and RF are suitable for modeling of syndrome differentiation of CF.
The method which combines CP and RF, namely CP-RF, was firstly proposed to deal with single-label classification problem in our previous work [36]. Unfortunately, CP-RF cannot be directly applied to syndrome differentiation of CF for it is a MLL problem. In this work, using Problem Transformation method, CP-RF is extended to handle MLL problem. To the best of our knowledge, it is the first time that CP is applied to MLL tasks.
The extended CP-RF was compared with two classical CP models CP-NBC (with Naive Bayes Classifier) and CP-KNN (with K-Nearest Neighbor) as well as the commonly used MLL algorithm in TCM, i.e. ML-KNN. Results of predictive effectiveness as well as some MLL-related evaluation metrics were reported. Especially, the validity of confidence measurement and the calibration property of CP-RF have been demonstrated. The experimental results show that CP-RF performs CP-NBC, CP-KNN and ML-KNN. In addition, the accuracy of CP-RF is higher than the confidence level, which reveals that the confidence evaluation of CP is valid and well-calibrated.
The remaining of this paper is organized as follows: in the Methods section the construction of the clinic CF dataset is introduced and the algorithmic process is proposed. In the Results section, the results of models constructed based on CP-RF, CP-NBC, CP-KNN and ML-KNN are compared. In the Discussion section, the reason that CP-RF can significantly improve the accuracy and provide valid confidence is discussed. The conclusive remarks followed in the Conclusion section.
Methods
Ethics Statement
N/A
Dataset of Chronic Fatigue in TCM
In past years, we have done a substantial amount of work on the diagnosis of CF in TCM [31]. As for CF diagnosis in TCM, 80% of clinical identification were provided by ‘interrogation’ manipulation (inquiry) [21]. Therefore, the standardization inquiry system shall influence the diagnosis and treatment of CF significantly. In the past, we have designed a quantitative inquiry form to obtain the standardized inquiring items for the identification of CF. Accordingly, we have made an epidemiological investigation among a large number of people that come from the south of Fujian Province during August 2007 to December 2008. The participators were further constrained to the doctors, nurses and the teachers who worked in the colleges, the middle school and primary school. The participators who has a continuous or recurring fatigue over six months was accumulated into the CF dataset and each of them was further clinically identified by another three clinical manipulations (‘inspection’, ‘auscultation-olfaction’ and ‘palpation’). As shown in Table 1, 95 symptoms were finally collected to construct the complete symptom set (feature set) of CF.
Table 1. Set of symptom of CF in TCM.
| ID | Symptoms | ||||
| 1–5 | depression | Fatigue afterexercise 24 hours | shortage of qi | pale complexion | sallow complexion |
| 6–10 | darkish complexion | bluish lip | gloomy complexion | fear of cold | fear of cold |
| 11–15 | vexing heat in thechest, palms and soles | afternoon fever | unsurfaced fever | tend to catch cold | spontaneous sweating |
| 16–20 | night sweating | pitting edema | cannot concentrate | amnesia | dim complexion |
| 21–25 | like sigh | thin | head stabbing pain | lassitude | heavy head |
| 26–30 | epilation or loose teeth | dry eyes | have a sudden blackoutwhen stand up | black eyes | tinnitus or deafness |
| 31–35 | dry throat | swollen pain inthe throat | discomfort in the throatlike something blockage | lymph node enlargement | lymph node tenderness |
| 36–40 | aching pain of neck | scurrying pain of theshoulder | stabbing pain of the waist | contracture of the back | oppression in the chest |
| 41–45 | palpitations | cough up thick phlegm | perennial cough | panting | stabbing pain in thechest or abdomen |
| 46–50 | distending and scurryingpain in the chest orabdomen | stuffiness andfullness in the chest | abdominal fullness | abdominal veins exposed | belching andacid vomiting |
| 51–55 | vomiting | abdominal distensionin the afternoonor after eating | numbness or paralysis | aching pain | distending pain |
| 56–60 | heavy body | encrusted skin | ache and weak in thewaist and kneeor heel pain | poor appetite | dry mouth |
| 61–65 | dry mouth and wantto drink | dry mouth butdon’t want to drink | bitter taste in the mouth | bland taste in the mouth | not thirst |
| 66–70 | insomnia | constipation | sloppy stool | sticky stool | stool sometimes sloppyand sometimes bound |
| 71–75 | reddish urine | yellow urine | frequent urination | copious and clear urine | dribbing urination |
| 76–80 | poor libido | dysmenorrhea | intermenstrual bleeding | menstrual irregularities | pale tongue |
| 81–85 | red tongue | enlarged tongue orteeth-marked tongue | spotted tongue | less fur | white and moist fur |
| 86–90 | yellow and slimy fur | string-like pulse | fine pulse | vacuous pulse | rough pulse |
| 91–95 | sunken pulse | relaxed pulse | slow pulse | rapid pulse | slippery pulse |
According to the principle of syndrome differentiation in TCM, each symptom has a certain degree of influence on all of the syndrome factors. The contributions of each symptom to all of the syndrome factors differ from the others, which can be referenced from the lexicon of “Differentiation standards for symptoms and signs of Chronic Fatigue Disease in Traditional Chinese Medicine”. The expression level of a syndrome factor is determined by the fusion of all statistical frequencies of the related symptoms. In our previous study, we found that the frequently expressed syndrome factors of CF are ‘spleen deficiency’, ‘heart deficiency’ ‘liver depression’, ‘qi deficiency’ ‘blood deficiency’, ‘kidney deficiency’, ‘blood stasis’, ‘yang deficiency’, ‘lung deficiency’, and ‘phlegm turbid’. However, from a practical viewpoint, the former four syndrome factors are widely employed in the clinic diagnosis of CF and the others remained ambiguous effect to CF [31]. Accordingly, the most frequently occurring syndrome factors in the clinical practice, i.e., ‘spleen deficiency’, ‘heart deficiency’, ‘liver depression’ and ‘qi deficiency’ are employed to diagnose CF in TCM. As a result, 736 patients construct the CF dataset for our experiment. Each case is described by 95 symptoms (features) and a subset of the four syndrome factors (labels). The dataset is shown in Dataset S1 and data information is shown in Data information S1.
Conformal Predictor
CP applies algorithmic randomness level associated with p-value scheme to measure the confidence of each label, and then selects the labels whose p-values are larger than a pre-defined significance level as the region prediction [32], [33]. A confidence level which is mutually complementary with the significance level is used to provide the confidence evaluation for the region prediction. The novelty of CP can be characterized by the calibration property of the region prediction, i.e. the accuracies of CP region prediction can be hedged by the confidence level. According to CP, given the training data sequence 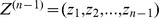 and the testing instance
and the testing instance 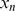 , CP assumes all the possible labels
, CP assumes all the possible labels 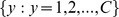 (C is the number of classes) being the candidate label for
(C is the number of classes) being the candidate label for 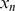 , and then establish the corresponding testing example
, and then establish the corresponding testing example 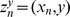 . Thus, the testing data sequence is constructed by
. Thus, the testing data sequence is constructed by 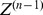 and each
and each 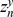 . Consequently, there are C test data sequences, i.e
. Consequently, there are C test data sequences, i.e
| (1) |
Secondly, CP applies algorithmic randomness statistical tests to test whether a particular testing data sequence 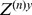 conforms to the independent and identical distribution (i.i.d.) or not. The algorithmic randomness level of
conforms to the independent and identical distribution (i.i.d.) or not. The algorithmic randomness level of 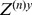 could be quantified by p-value, noted as
could be quantified by p-value, noted as 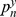 . Intuitively, a small p-value means that
. Intuitively, a small p-value means that 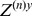 may not be an i.i.d. data sequence. It further implies that the corresponding candidate label
may not be an i.i.d. data sequence. It further implies that the corresponding candidate label 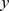 may not be the true label and should be discarded from the region prediction.
may not be the true label and should be discarded from the region prediction.
CP applies a unique method to construct the statistic p-value. CP designs a function 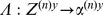 , which maps each example
, which maps each example 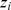 to a nonconformity score
to a nonconformity score 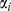 , and thus establishes a one-dimension nonconformity score sequence:
, and thus establishes a one-dimension nonconformity score sequence:
| (2) |
where 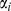 measures the degree of the nonconformity between
measures the degree of the nonconformity between 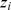 and
and 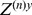 . Based on
. Based on 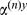 , p-value is defined as follows:
, p-value is defined as follows:
| (3) |
In the end, the significance level ε,which reveals the smallest threshold of the acceptation of a particular testing data sequence 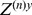 being the i.i.d. hypothesis, is used to be the threshold. Thus any testing data sequence
being the i.i.d. hypothesis, is used to be the threshold. Thus any testing data sequence 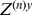 whose p-values are larger than the significance level should be the legal label and can serve as the true label. So CP outputs region prediction for
whose p-values are larger than the significance level should be the legal label and can serve as the true label. So CP outputs region prediction for 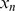 as follows,
as follows,
| (4) |
An error occurs when the prediction set 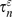 does not contain the true label
does not contain the true label 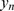 of the testing instance
of the testing instance 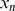 . It has been proven that in online learning setting the error rate of CP is not greater than significance level
. It has been proven that in online learning setting the error rate of CP is not greater than significance level
 , i.e.,
, i.e.,
| (5) |
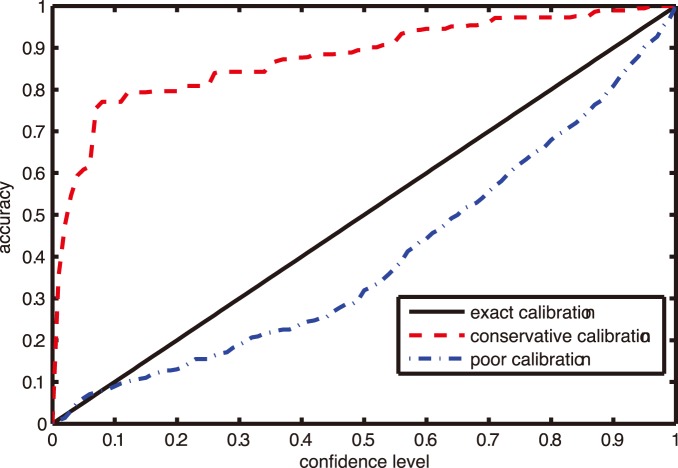
The inequality (5) shows that the error rate of CP is bounded by the significance level. In the view of confidence level which is mutually complementary with the significance level, the accuracy of CP is hedged by the confidence level [34]. The relationship between accuracy and confidence level shows the calibration property of CP. Given different confidence levels, the performance of the corresponding CP accuracies is illustrated in Fig. 1. The abscissa represents the confidence level and the ordinate represents the corresponding accuracy of CP. In Fig. 1, the diagonal line with the legend of ‘exact calibration’ indicates that the accuracies of CP are equal to the corresponding confidence levels, and the accuracy rate curve hovering over exact calibration line denotes a conservative calibration property, while the curve lying below the diagonal line shows a poor calibration. In online setting, CP possesses exact or conservative calibration property in its region prediction, which enables it to provide valid confidence evaluation for its prediction.
Figure 1. An illustrative example of calibration property.
According to CP, the computation of the nonconformity score 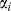 of
of 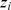 can be obtained generally by traditional machine learning algorithms, such as Support Vector Machine (SVM), K Nearest Neighbor (KNN) and Naïve Bayes classifier (NBC) [35]. CP-NBC plugs Naïve Bayes classifier (NBC) into the framework of CP which designs the posterior probability of label as the confidence measure, while CP-KNN designs the nonconformity score of example based on the Euclidean distances between the testing instance and its K nearest neighbor [35].
can be obtained generally by traditional machine learning algorithms, such as Support Vector Machine (SVM), K Nearest Neighbor (KNN) and Naïve Bayes classifier (NBC) [35]. CP-NBC plugs Naïve Bayes classifier (NBC) into the framework of CP which designs the posterior probability of label as the confidence measure, while CP-KNN designs the nonconformity score of example based on the Euclidean distances between the testing instance and its K nearest neighbor [35].
Considering the categorical characteristic of CF data which present a big challenge for the application of some distance metric-based algorithms, such as SVM and KNN, we plugged Random Forest (RF) into the framework of CP to construct CP-RF model for the syndrome differentiation of CF. RF is one of the most successful ensemble methods, which uses CART as its meta classifier [28]. RF repeats to draw bootstrap examples from the original dataset and then establishes ntree un-pruned CART trees. At each node of the CART tree, RF chooses randomly mtry features from the complete set of features to split. Based on the model of RF, a proximity measure between instances can be established. If instance 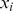 and
and 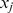 both land in the same terminal node of a CART tree, the proximity between them is increased by one, and the overall proximities, denoted as
both land in the same terminal node of a CART tree, the proximity between them is increased by one, and the overall proximities, denoted as 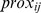 can be computed across all the CART trees. The nonconformity score based RF proximity is designed as follows:
can be computed across all the CART trees. The nonconformity score based RF proximity is designed as follows:
| (6) |
where K is the number of nearest neighbors, 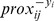 stands for the
stands for the 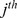 largest proximity between instance
largest proximity between instance 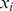 and the instances labelled differently from
and the instances labelled differently from 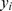 ;
; 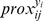 stands for the
stands for the 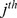 largest proximity between instance
largest proximity between instance 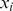 and the instances with the same label
and the instances with the same label 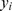 . The intuition behind Equation (6) is that, two instances
. The intuition behind Equation (6) is that, two instances 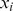 and
and 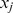 with the same label will tend to have a large proximity value and the two with different labels will have a small one. Thus the corresponding nonconformity score
with the same label will tend to have a large proximity value and the two with different labels will have a small one. Thus the corresponding nonconformity score 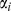 will be rather small, and vice versa. Therefore, the nonconformity measurement can exactly reflect the nonconformity of the example [36], [37].
will be rather small, and vice versa. Therefore, the nonconformity measurement can exactly reflect the nonconformity of the example [36], [37].
Multi-label Learning
In some pattern recognition tasks, the pattern of an instance can be described by multiple labels simultaneously. An image can be referred by multiple elements, such as mountain, lake and tree. The thematic topics of a text can include politic and education simultaneously [38]–[42]. Given each label 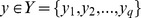 where Y denotes the label space with q possible class, the task of MLL is to learn a real valued function
where Y denotes the label space with q possible class, the task of MLL is to learn a real valued function 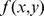 which measures the confidence of y being the proper label of x. Thus given a specified threshold
which measures the confidence of y being the proper label of x. Thus given a specified threshold 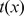 , the MLL classifier should output the prediction
, the MLL classifier should output the prediction 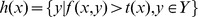 , where
, where 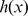 shows obviously to be a region prediction.
shows obviously to be a region prediction.
According to whether the multi-label examples would be transformed before modeling or not, the MLL algorithms can be divided into two categories: Problem Transformation methods (PT) and Algorithm Adaptation methods (AA) [17], [19]. PT method splits the multi-label examples straightforward into single-label examples and then applies single-label machine learning algorithms to tackle the multi-pattern recognition problem. Generally, six PT strategies have been reported in this issue. For example, the commonly used PT4 method transforms the original data set into q data sets. Each of them constructs a binary dataset which extracts the training instances relevant to a particular label as positive examples and the rest to be the negative examples. After applying the traditional machine learning algorithms to construct classifiers based on the q binary datasets, there must be a post-process mapping the traditional single-label outputs to multi-label prediction [43]. On the other hand, AA method adapts traditional single-label algorithms, such as KNN, SVM and boosting classifier to fit the multi-label data. The representative algorithms is ML-KNN [44]. For the testing instance x, the confidence score of each label is the posterior probability which is computed based on its K nearest distances and its conditional probability. Then the labels whose posterior probability are larger than a specific threshold (e.g., 0.5) should be selected as the prediction output.
Using Conformal Predictor for Multi-label Learning
The main purpose of this work is to use CP method to construct an effective and reliable diagnostic tool for CF syndrome differentiation. CP outputs region prediction rather than point prediction, which makes it competent for the multi-label recognition task. However, the traditional machine learning algorithms which are plugged into the framework of CP to compute the nonconformity score of each example are always single-label machine learning algorithms. How to involve the multi-label examples into the framework of CP, i.e., how to measure the nonconformity score of each multi-label example and how to test the confidence level of a multi-label data sequence conforming to the i.i.d. assumption, has been the critical issue when using CP for multi-label learning.
In this study, in order to use CP in multi-label learning, we applied a simple and intuitive method, i.e., PT5 method [17]. Each multi-label instance x with a total l labels reproduces l single-label examples. As illustrated in Fig. 2, the patient (ID number 1) who has been diagnosed as (‘spleen deficiency’, ‘liver depression’, ‘qi deficiency’) will reproduce three instances with label ‘spleen deficiency’, ‘liver depression’ and deficiency’ respectively. With this method, the original multi-label CF dataset have transformed to a new single-label dataset which is suitable for single-label machine learning algorithms, such as NB, KNN and RF. Then CP-NBC, CP-KNN and CP-RF can be introduced to CF syndrome differentiation. When to predict a patient, CP-RF applies RF to measure the confidence level namely p-value of each label (syndrome factor) being the true label, and then selects multiple labels whose p-values are larger than the pre-defined significance level (threshold) as the region prediction. The confidence level which is mutually complementary with the significance level serves as the confidence evaluation for the region prediction.
Figure 2. An illustrative example of the PT5 method.
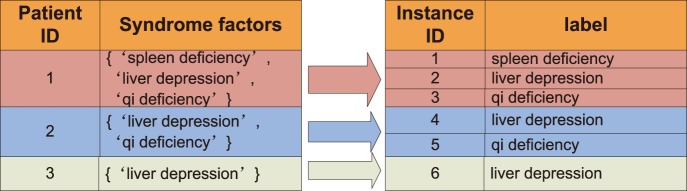
Using PT5 method for data transformation and RF algorithm for nonconformity score computation, the algorithmic process of CP for multi-label learning is described as follows. The R code is shown in Code S1.
Algorithm 1: CP-RF for Multi-Label Learning
Input: 1. Training data sequence 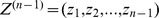 where each data
where each data 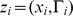 and
and 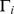 is the multi-label designation of instance
is the multi-label designation of instance 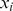 .
.
2. A testing instance 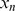
3. Significance level 
4. The parameters ntree, mtry of RF
5. The parameter K for nonconformity measurement
Output: region prediction 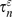
-
Applies problem transformation method(PT5) to get new training data sequence
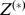
Initiating
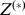 to be an empty set.
to be an empty set.-
for each data
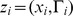
Measuring the size of
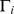 to be
to be 
Reproducing the instance
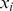 to the total of
to the total of  instances.
instances.Designating each of the labels in
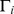 to the
to the  instance correspondingly.
instance correspondingly.Adding the new
 single-label examples into the transformed
single-label examples into the transformed 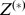 .
.
-
Outputs the region prediction for instance
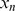 base on
base on 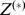 with the size of which being
with the size of which being 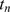
Using
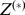 to construct RF model with the parameter ntree, mtry
to construct RF model with the parameter ntree, mtry
Exporting the proximity matrix
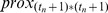 for the validating instance
for the validating instance 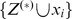 .
.-
for
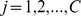 with
with  is the number of multiple labels
is the number of multiple labelsApplying equation (6) to obtain a serial of
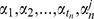 with the parameter K
with the parameter K
Applying equation (3) to compute the algorithmic randomness level
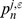
Applying equation (4) to obtain the region output
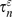
Experimental Design and Evaluation
Experiment Setup
The CP-RF model is compared with two classical CP models CP-NBC and CP-KNN as well as the commonly used ML-KNN in TCM. The detailed algorithm and parameter settings of CP-NBC and CP-KNN can be found in [35] and for MLL-KNN we refer to [21]. For CP-RF, the parameter ntree of RF is set to 1000 which is large enough, and mtry is 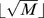 where M is the number of symptoms (features). The number of neighbors, K, which is required for CP-RF, CP-KNN and ML-KNN, we tried different values as K = 1, 3, 5, 7, 9,11.
where M is the number of symptoms (features). The number of neighbors, K, which is required for CP-RF, CP-KNN and ML-KNN, we tried different values as K = 1, 3, 5, 7, 9,11.
All the algorithms were executed in leave-one-out cross-validation (LOOCV), which uses every single example of the original data set as the testing data, and the remaining examples as the training data in each fold. Compared with commonly used 5-fold and 10-fold cross-validation method, with LOOCV we can obtain more testing data to validate the statistical calibration property of the result on CF dataset.
Evaluation Metric
Considering the particular multi-label learning setting, the evaluation metrics are different from metrics used in single-label learning. Given a pre-defined threshold 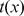 , the MLL classifier will output the region prediction
, the MLL classifier will output the region prediction 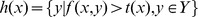 . Let the result of label ranking for the testing instance
. Let the result of label ranking for the testing instance 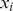 denoted as
denoted as 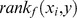 , which is a one-to-one mapping onto
, which is a one-to-one mapping onto 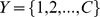 such that if
such that if 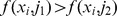 then
then 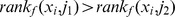 where
where 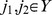 . And the test dataset
. And the test dataset 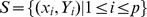 , where
, where 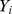 is the true label set for instance xi and p is the size of test dataset. Based on the above definition, the MLL-related evaluation metrics can be defined as follows [17], [19].
is the true label set for instance xi and p is the size of test dataset. Based on the above definition, the MLL-related evaluation metrics can be defined as follows [17], [19].
- Subset Accuracy: The subset accuracy evaluates the accuracy of the multi - label classifier, which computes the fraction of the prediction region being identical to the true label set.
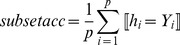
(7) - Hamming Loss: The hamming loss evaluates the fraction of misclassified instance-label pairs, i.e. a relevant label is missed or an irrelevant is predicted.
where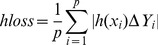
(8) 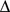 stands for the symmetric difference between two sets.
stands for the symmetric difference between two sets. - One-error: The one-error evaluates the fraction of examples whose top-ranked label is not in the true label set.
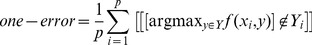
(9) - Coverage: The coverage evaluates how many steps are needed, on average, to move down the ranked label list so as to cover all the true labels of the example.

(10) - Ranking Loss: The ranking loss evaluates the fraction of reversely ordered label pairs, i.e., an irrelevant label is ranked higher than a relevant label.
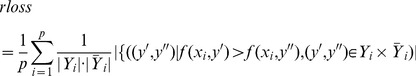
(11) Average Precision: the average precision evaluates the average fraction of relevant labels ranked higher than a particular label actually being in the label set.
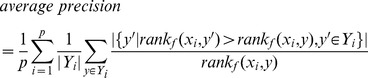 |
(12) |
According to the definition of the above six metrics, the higher the values of subset accuracy and average precision are preferred whereas the lower the values of hamming loss, one-error, coverage and ranking loss are welcome. Among them, subset accuracy and hamming loss evaluate the predictive effectiveness of the MLL model and are the most widely-used metrics in the MLL community.
Verification of Reliability
As mentioned in Methods section, the most significant advantage of CP is the calibration property of its prediction, i.e., the error rate is exactly bounded by the predefined significance level. The calibrated prediction which provides valid confidence to evaluate the reliability of prediction is highly preferred to medical practitioners.
Theoretically, CP is well calibrated in the online setting. but extensive empirical studies have demonstrated that CP still shows good calibration property in batch learning, where the learning tasks are conducted by off-line learning [45], [46]. A typical example of this is the medical diagnosis, where only after a period of treatment can the prognostic information(true label) be obtained and thus the true label cannot be added timely for on-line learning. In this study we will empirically investigate the calibration property of CPs on CF dataset in LOOCV experiments.
Further, in previous studies, the calibration property of CP has only been tested on a single - label dataset. To the best of our knowledge, it is the first time that CP is applied to MLL tasks. Whether the calibration property still holds in MLL remains unknown in theory. Similar to single-label learning setting, we define the calibration property of MLL classifiers as follows: The risk of the true label set not being the subset of the prediction output is not greater then a specific significance level ε, i.e.,
| (13) |
Results
For a specified threshold, all the six evaluation metrics were computed based on the test data to evaluate the predictive performance of MLL classifiers. Given a series of different threshold values, the MLL classifiers output different prediction regions. For CP models, the threshold corresponds to a significance level while that of ML-KNN corresponds to posterior probability. In this sense, the preferred threshold values of CPs should be chosen from (0, 0.5) while the values of threshold of ML-KNN should be chosen from (0.5, 1). For the convenience of comparison, we use a confidence level (one minus significance level) as the threshold for CPs. Consequently, for all the algorithms, the higher the threshold is, the more reliable the prediction is. And the threshold values should range from 0.5 to 1, which is highly preferred in TCM practice.
Comparison on Subset Accuracy and Hamming Loss
In this subsection, we compare the most commonly used metric - subset accuracy and hamming loss. The results of CP-RF, CP-NBC, CP-KNN and ML-KNN with parameter K = 1 were compared in Fig. 3–4, with the X axes representing the threshold value and the Y axes representing the subset accuracy and hamming loss respectively.
Figure 3. Comparison of subset accuracy with different thresholds.
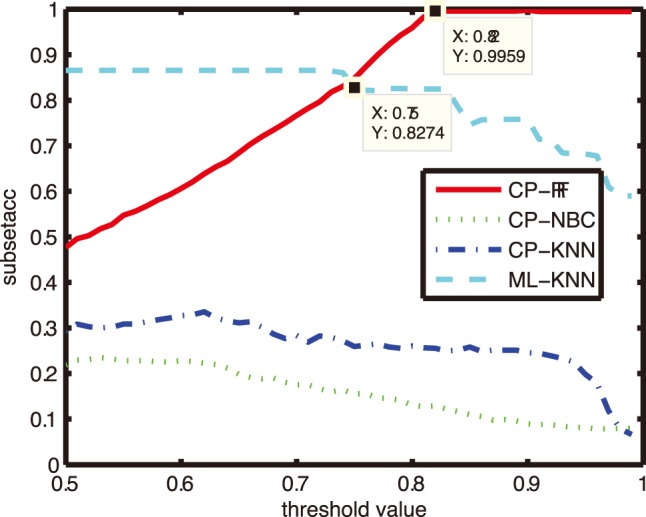
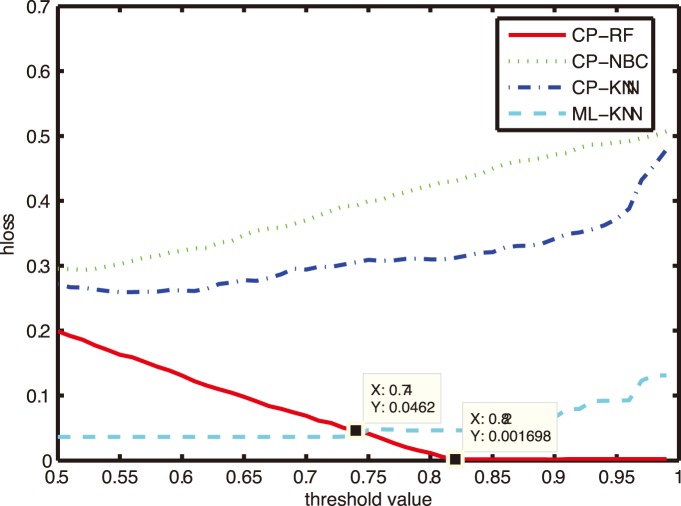
Figure 4. Comparison of hamming loss with different thresholds.
Fig. 3 illustrates the variation of subset accuracy with different threshold values from 0.5 to 1. From Fig. 3, we can see that the performances of CP-NBC,CP-KNN and ML-KNN deteriorate with the increase of the threshold, while the performance of CP-RF getting better. ML-KNN and CP-RF outperform CP-NBC and CP-KNN across the region (0.5, 1). CP-RF beats ML-KNN after the threshold value of 0.75 and CP-RF obtains the highest value 0.9959 of subset accuracy after the threshold value of 0.82.
The similar result can also be found from Fig. 4. The hamming loss of CP-NBC, CP-KNN and ML-KNN exhibit an increasing trend with the increase of a threshold value, while CP-RF gets lower hamming loss when the threshold value increases. Similarly, the performances of ML-KNN and CP-RF are significantly better than CP-NBC and CP-KNN across the region (0.5, 1). CP-RF outperforms ML-KNN after the threshold value of 0.75 and it obtains a lowest hamming loss value of 0.01698 after the threshold value of 0.82.
As discussed above, a higher threshold (higher confidence level or larger posterior probability) is preferred to medical practitioners. In this sense, CP-RF is a more effective and reliable classifier than ML-KNN and other CP models for CF diagnosis.
Further, in this study, CP-RF gets the same region prediction (high subset accuracy) at different thresholds ranging from about 0.8 to 1(high confidence level). In this sense, the size of prediction region, i.e., the number of syndrome factors selected by CP-RF model, is robust with the threshold determination to some context. The threshold determination remains an unsolved issue in MLL literatures [47]. The prior knowledge of the optimal threshold value has been always unavailable, except that a high confidence level is more preferred. As an example, we can see from Fig. 3 and Fig. 4, for ML-KNN, CP-NBC and CP-KNN, the performance always deteriorates with the increase of the threshold value. Researchers always have to trade-off between the reliability (higher threshold values) and effectiveness (performances) of the MLL classifiers. For example, Li et.al. set the threshold value to be 0.5 empirically [22], [48]. However, in this study, CP-RF does not suffer from this problem. Such merit provides marked significance for TCM syndrome differentiation.
The Influence of Different K Values on Subset Accuracy and Hamming Loss
In order to investigate whether the K values will influence the performances of MLL classifiers, in this subsection we compare the 4 algorithms on subset accuracy and hamming loss with different K values. Results at three preferred confidence levels of 0.99, 0.9 and 0.8 were shown in Table 2 and Table 3. Limited by space, we only show the results with K = 5, 9 and 11.
Table 2. Comparisons of subset accuracy with different K values.
| K = 5 | K = 9 | K = 11 | |||||||
| Confidence level | 0.99 | 0.90 | 0.80 | 0.99 | 0.90 | 0.80 | 0.99 | 0.90 | 0.80 |
| CP-RF | 0.94 | 0.97 | 0.98 | 0.93 | 0.97 | 0.99 | 0.93 | 0.97 | 0.99 |
| CP-NBC | 0.04 | 0.24 | 0.26 | 0.049 | 0.24 | 0.26 | 0.04 | 0.240 | 0.26 |
| CP-KNN | 0.10 | 0.33 | 0.38 | 0.10 | 0.31 | 0.37 | 0.10 | 0.34 | 0.40 |
| ML-KNN | 0.72 | 0.72 | 0.73 | 0.50 | 0.78 | 0.78 | 0.47 | 0.73 | 0.82 |
Table 3. Comparisons of hamming loss with different K values.
| K = 5 | K = 9 | K = 11 | |||||||
| Confidence level | 0.99 | 0.90 | 0.80 | 0.99 | 0.90 | 0.80 | 0.99 | 0.90 | 0.80 |
| CP-RF | 0 | 0 | 0.01 | 0.02 | 0.01 | 0 | 0.02 | 0.901 | 0 |
| CP-NBC | 0.51 | 0.47 | 0.43 | 0.51 | 0.33 | 0.29 | 0.50 | 0.31 | 0.24 |
| CP-KNN | 0.51 | 0.35 | 0.31 | 0.50 | 0.35 | 0.31 | 0.51 | 0.35 | 0.31 |
| ML-KNN | 0.08 | 0.08 | 0.08 | 0.12 | 0.10 | 0.04 | 0.18 | 0.07 | 0.05 |
From Table 2, with different K values, CP-RF still performs the best compared with other algorithms at the specified confidence levels. The subset accuracy of all the four algorithms varies lightly with the variation of K values. Among them the fluctuations of CP-RF shows relatively small. Therefore, the performances of these algorithms are highly robust to the setting of K. The similar conclusion can be achieved from Table 3.
Comparison on other Evaluation Metrics
In order to further investigate the reliability and effectiveness of CP-RF models in the CF diagnosis, performances on other four evaluation metrics were reported. Fig. 5–8 shows the performance of four algorithms with parameter K = 1, and the comparative results with K = 5, 9 and 11 at three interested confidence levels of 0.99, 0.9 and 0.8 were listed in the Table 3–6.
Figure 5. Comparison of one-error with different thresholds.
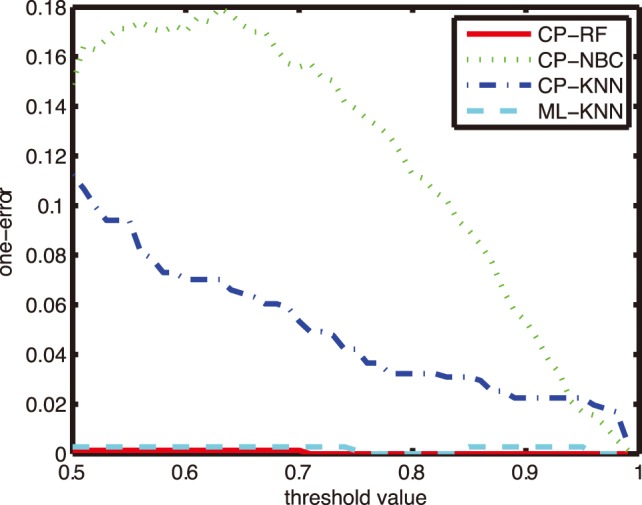
Figure 8. Comparison of average precision with different thresholds.
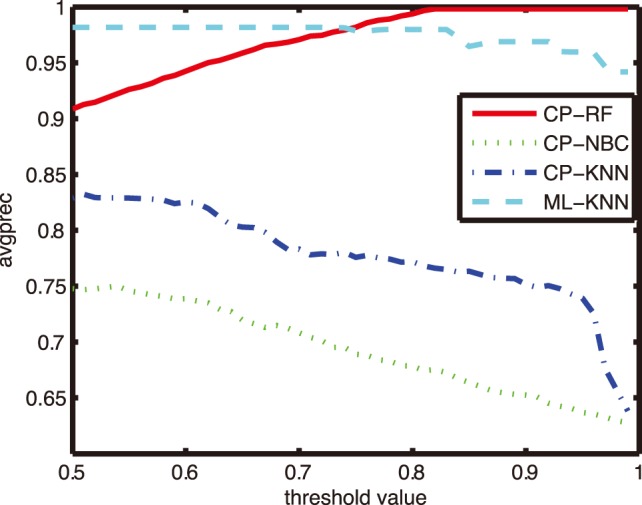
Table 6. Results of ranking loss metric with different K values.
| K = 5 | K = 9 | K = 11 | |||||||
| Confidence level | 0.99 | 0.90 | 0.80 | 0.99 | 0.90 | 0.80 | 0.99 | 0.90 | 0.80 |
| CP-RF | 0.02 | 0.01 | 0.01 | 0.03 | 0.01 | 0.01 | 0.03 | 0.01 | 0.01 |
| CP-NBC | 0.90 | 0.51 | 0.43 | 0.90 | 0.56 | 0.50 | 0.89 | 0.50 | 0.40 |
| CP-KNN | 0.95 | 0.58 | 0.49 | 0.93 | 0.58 | 0.49 | 0.94 | 0.58 | 0.49 |
| ML-KNN | 0.23 | 0.20 | 0.08 | 0.29 | 0.11 | 0.09 | 0.34 | 0.14 | 0.09 |
Figure 6. Comparison of coverage with different thresholds.
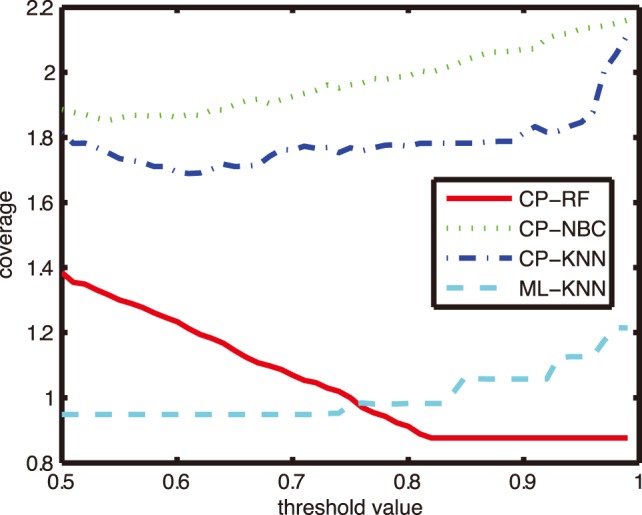
Figure 7. Comparison of ranking loss with different thresholds.
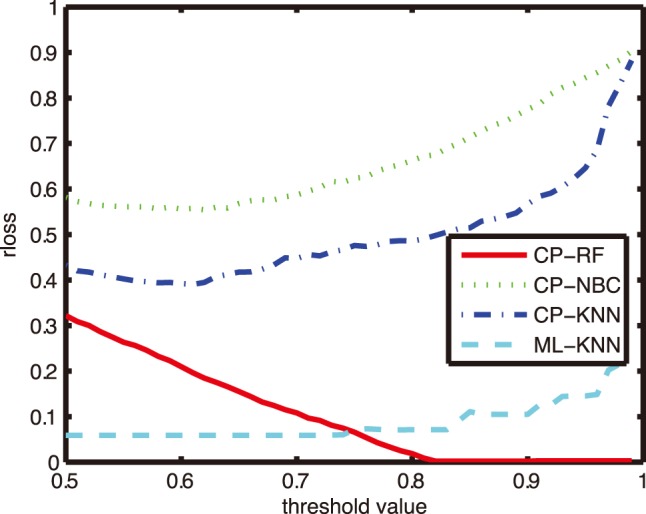
Table 5. Results of coverage metric with different K values.
| K = 5 | K = 9 | K = 11 | |||||||
| Confidence level | 0.99 | 0.90 | 0.80 | 0.99 | 0.90 | 0.80 | 0.99 | 0.90 | 0.80 |
| CP-RF | 0.90 | 0.88 | 0.88 | 0.90 | 0.89 | 0.88 | 0.91 | 0.89 | 0.88 |
| CP-NBC | 2.15 | 1.63 | 1.51 | 2.16 | 1.68 | 1.62 | 2.14 | 1.63 | 1.49 |
| CP-KNN | 2.20 | 1.83 | 1.78 | 2.17 | 1.83 | 1.78 | 2.19 | 1.83 | 1.78 |
| ML-KNN | 1.17 | 1.13 | 0.98 | 1.23 | 1.00 | 1.00 | 1.31 | 1.03 | 1.00 |
As can be seen from Fig. 5–8, in case of three metrics, i.e., one error, coverage and ranking loss, which prefer small value, CP-RF achieve significantly small values which outperform the other three algorithms. Whereas in case of average precision metric which prefers high value, the CP-RF can get a significantly high value close to 1. The similar trend and result have been demonstrated in Table 4–7, regardless of the difference K values. The results in Fig. 5–8 and Table 4–7 indicate again that CP-RF would be a more effective and reliable tool for CF diagnosis.
Table 4. Results of one-error metric with different K values.
| K = 5 | K = 9 | K = 11 | |||||||
| Confidence level | 0.99 | 0.90 | 0.80 | 0.99 | 0.90 | 0.80 | 0.99 | 0.90 | 0.80 |
| CP-RF | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| CP-NBC | 0. | 0 | 0.01 | 0 | 0.01 | 0.06 | 0 | 0.01 | 0.01 |
| CP-KNN | 0 | 0.02 | 0.03 | 0 | 0.02 | 0.03 | 0.01 | 0.02 | 0.03 |
| ML-KNN | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.03 |
Table 7. Results of average precision metric with different K values.
| K = 5 | K = 9 | K = 11 | |||||||
| Confidence level | 0.99 | 0.90 | 0.80 | 0.99 | 0.90 | 0.80 | 0.99 | 0.90 | 0.80 |
| CP-RF | 0.99 | 0.99 | 1.00 | 0.99 | 0.99 | 1.00 | 0.98 | 0.99 | 1.00 |
| CP-NBC | 0.63 | 0.76 | 0.79 | 0.63 | 0.74 | 0.76 | 0.63 | 0.76 | 0.80 |
| CP-KNN | 0.62 | 0.75 | 0.77 | 0.63 | 0.75 | 0.77 | 0.62 | 0.75 | 0.77 |
| ML-KNN | 0.90 | 0.91 | 0.97 | 0.90 | 0.92 | 0.97 | 0.86 | 0.95 | 0.96 |
The Calibration Property of CP Models
In this subsection, we present a preliminary empirical investigation on the calibration property of CP on the CF dataset. Given different confidence levels, the corresponding accuracies were reported in Fig.9 for three CP models, i.e., CP-RF, CP-NBC and CP-KNN with K = 1. The X axis represents a series of different confidence levels and the Y axis strands for accuracy.
Figure 9. Calibration property of CPs on CF dataset.
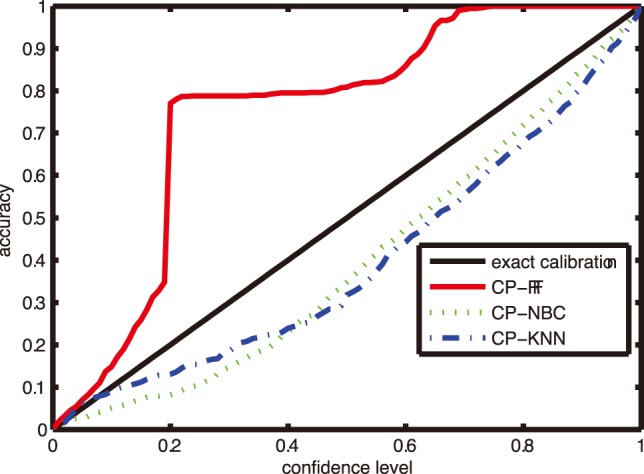
From Fig.9, we can see that the accuracy calibration line of CP-RF displays significantly beyond the exact calibration line, while the results of CP-KNN and CP-NBC show poor calibration. In this sense, CP-RF also outperforms CP-NBC and CP-KNN. The main reason may lie in the learning setting. Because the calibration property cannot be guaranteed theoretically in batch learning mode, in this case different nonconformity measurement with different algorithms (i.e. RF, KNN, and NBC) has a great impact on the performance of CP. The superiority of CP-RF will be explained in the Discussion section.
Discussion
Applicability of CP-RF Model for Chronic Fatigue Syndrome Differentiation
According to TCM theory, TCM diagnosis by the syndrome factor set is different from traditional single-pattern classification, and cannot be addressed by traditional single-label classifier. Attempts to solve the syndrome differentiation of CF have resulted in the development of multi-label learning, which can involve the complex interaction among different syndrome factors. Generally, the syndrome differentiation of chronic fatigue falls into multi-label classification setting [21], [49], [50].
Conformal Predictor (CP) can output region prediction tailed by valid confidence, which enables it to be a natural solution of multi-label learning. However, using CP for multi-label learning has not yet been studied. In this study, we applied it to chronic fatigue syndrome differentiation and verified its effectiveness and reliability.
Different CP models were used in this study, such as CP-NBC, CP-KNN and CP-RF. Among them, CP-RF which applies RF to compute the nonconformity score, achieved the best performance. The main reason may lie in the merits of the RF model when facing with CF dataset. RF highlights its superiority on the categorical CF dataset in TCM. The inferiority of CP-NBC may lie in the great dependency among the symptoms which deteriorates the performance of Naïve Bayes classifier, and the performances of CP-KNN and ML-KNN are affected by the categorical characteristic of the CF symptom.
The results also show that CP-RF remains steadily outstanding performance regardless of any threshold value among the region of (0.8, 1). Consequently, the size of prediction region, i.e., the number of syndrome factors selected by CP-RF model, is robust to the user-defined threshold, which remains an unsolved issue in many multi-label learning methods such as MLL-KNN [51], [52]. The robustness of CF syndrome differentiation by CP-RF has practical significance. Due to the substantially large amount of people suffer from CF, enormous health care resources tend to be consumed by patients with CF. However, different with acute illness that must be taken care of medical physician, CF treatments are mostly executed outside of the hospital. If the diagnosis of CF can be offered by the reliable computer-based intelligent tool using CP-RF, the patient can engage their own health more convenient and timely. In this sense, CP-RF can be employed as family-service equipment for the prevention and control for CF, which can dramatically relieve the burden of health care system.
Further, compared with ML-KNN, CP also offers valid confidence in the prediction region. The prediction region of CP is well-calibrated that the accuracy of region prediction is hedged by the specified confidence level.
Contribution of CP-RF Model for Multi-label Learning
This study also indicated that CP can serve as a reliable MLL model. In details, the region prediction 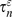 corresponds to
corresponds to 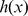 , the algorithmic randomness level
, the algorithmic randomness level 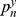 can be used as confidence scores for each possible label, and the significance level
can be used as confidence scores for each possible label, and the significance level  acts as the threshold determination. In this manner, the reliability or risk analysis of the prediction is emphasized, which is often neglected in MLL literatures.
acts as the threshold determination. In this manner, the reliability or risk analysis of the prediction is emphasized, which is often neglected in MLL literatures.
Secondly, few studies have focused on the use of random forest in MLL. CP-RF which plugs RF into CP framework achieves superior performance on CF dataset and provides an alternative way of using random forest in MLL. In conclusion, CP-RF is a promising method for the MLL.
Conclusions
Chronic fatigue syndrome differentiation has been formulated as a multi-label learning task. We plug random forest (RF) into the framework of conformal predictor (CP) to establish a reliable and effective diagnostic tool. Combined with PT5 method, CP-RF is extended to handle multi-label learning tasks. CP-RF outperforms CP-NBC, CP-KNN and MLL-KNN. Noted that in TCM medical diagnosis which is always conducted in batch learning mode, CP-RF still shows conservative calibration and provides valid confidence evaluation for the CF syndrome differentiation, which would be preferred to TCM practitioners.
Supporting Information
R code of CP-RF for Multi-Label Learning.
(R)
Inclusion criteria of the patients, Diagnosis criteria, Exclusion criteria, Data Collection, Data Description of the Chronic Fatigue dataset used in this study.
(DOCX)
The Chronic Fatigue dataset used in this study. 736 patients construct the CF dataset and each case is described by 95 symptoms (features) and a subset of the four syndrome factors (labels).
(TXT)
Acknowledgments
We are grateful to Dr. Xueqin Hu for helpful discussion about the professional explanation of chronic fatigue in TCM.
Funding Statement
The work is supported by National Natural Science Fundation of China under Grant No. 61202144, No.61203282 and No.61300138, Natural Science Foundation of Fujian Province China, under Grant No.2012J01274 and No. 2012J05125, The Research Grant Council of Huaqiao University under Grant No. 09BS515. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Fukuda K, Straus SE, Hickie I, Sharpe MC, Dobbins JG, et al. (1994) The chronic fatigue syndrome: a comprehensive approach to its definition and study. Annals of internal medicine 121: 953–959. [DOI] [PubMed] [Google Scholar]
- 2. Prasko J, Kovacsova A, Jelenova D, Latalova K (2010) Chronic fatigue syndrom and its treatment–psychiatric view. Activitas Nervosa Superior Rediviva 52: 104–113. [Google Scholar]
- 3. McCrone P, Sharpe M, Chalder T, Knapp M, Johnson AL, et al. (2012) Adaptive pacing, cognitive behaviour therapy, graded exercise, and specialist medical care for chronic fatigue syndrome: a cost-effectiveness analysis. Plos One 7: e40808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Chen R, Moriya J, Yamakawa J, Takahashi T, Kanda T (2010) Traditional Chinese medicine for chronic fatigue syndrome. Evidence-Based Complementary and Alternative Medicine 7: 3–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Alraek T, Lee M, Choi TY, Cao H, Liu J (2011) Complementary and alternative medicine for patients with chronic fatigue syndrome: a systematic review. BMC complementary and alternative medicine 11: 87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Wang J, Xiong X (2012) Current situation and perspectives of clinical study in integrative medicine in China. Evidence-Based Complementary and Alternative Medicine 2012: 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Feng Y, Wu Z, Zhou X, Zhou Z, Fan W (2006) Knowledge discovery in traditional Chinese medicine: state of the art and perspectives. Artificial Intelligence In Medicine 38: 219–236. [DOI] [PubMed] [Google Scholar]
- 8. Lukman S, He Y, Hui S (2007) Computational methods for traditional Chinese medicine: a survey. Computer Methods and Programs in Biomedicine 88: 283–294. [DOI] [PubMed] [Google Scholar]
- 9. Zhou WF (2002) Standardization Research of Differentiation System of Symptoms and Signs and Syndrome in TCM. Gianjin Journal of Traditional Chinese Medicine 19: 1–4. [Google Scholar]
- 10. Zhu W, He J, Yan J, Huang B (2007) Algorithm of double levels of frequency and weight to determine the weight value for syndrome factor differentiation. Journal of Chinese Integrative Medicine 5: 607–611. [DOI] [PubMed] [Google Scholar]
- 11. Jiang M, Lu C, Zhang C, Yang J, Tan Y, et al. (2012) Syndrome differentiation in modern research of traditional Chinese medicine. Journal of Ethnopharmacology 140: 634–642. [DOI] [PubMed] [Google Scholar]
- 12. Luo H, Han Z, Li J, Ma R, Yuan Q, et al. (2007) Study on regularity of Traditional Chinese Medicine Syndrome in precancerous lesion of stomach cancer. China Journal of Traditional Chinese Medicine and Pharmacy 22: 399–401. [Google Scholar]
- 13. Chen R, Wong C, Lam T (2012) Construction of a traditional Chinese medicine syndrome-specific outcome measure: the Kidney Deficiency Syndrome questionnaire (KDSQ). BMC complementary and alternative medicine 12: 73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Song YN, Zhang GB, Zhang YY, Su SB (2013) Clinical Applications of Omics Technologies on ZHENG Differentiation Research in Traditional Chinese Medicine. Evidence-Based Complementary and Alternative Medicine 2013: 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Dai J, Sun S, Cao H, Zheng N, Wang W, et al. (2012) Applications of new technologies and new methods in ZHENG differentiation. Evidence-Based Complementary and Alternative Medicine 2012: 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Su SB (2013) Recent Advances in ZHENG Differentiation Research in Traditional Chinese Medicine. International Journal of Integrative Medicine 1: 1–10. [Google Scholar]
- 17. Tsoumakas G, Katakis I (2007) Multi-label classification: An overview. International Journal of Data Warehousing and Mining (IJDWM) 3: 1–13. [Google Scholar]
- 18.Streich A, Buhmann J (2008) Classification of Multi-labeled Data: A Generative Approach. Machine Learning and Knowledge Discovery in Databases : 390–405.
- 19. Zhang M, Zhou Z (2013) A Review On Multi-Label Learning Algorithms. IEEE Transactions on Knowledge and Data Engineering 99 1–42. [Google Scholar]
- 20. Madjarov G, Kocev D, Gjorgjevikj D, Džeroski S (2012) An extensive experimental comparison of methods for multi-label learning. Pattern Recognition 45: 3084–3104. [Google Scholar]
- 21. Liu GP, Li GZ, Wang YL, Wang YQ (2010) Modelling of inquiry diagnosis for coronary heart disease in traditional Chinese medicine by using multi-label learning. BMC complementary and alternative medicine 10: 37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Li GZ, Yan SX, You M, Sun S, Ou A (2012) Intelligent ZHENG Classification of Hypertension Depending on ML-kNN and Information Fusion. Evidence-Based Complementary and Alternative Medicine 2012 doi:10.1155/2012/837245.
- 23.Melluish T, Saunders C, Nouretdinov I, Vovk V (2001) Comparing the Bayes and Typicalness Frameworks. 12th European Conference on Machine Learning: 360–371.
- 24.Vovk V, Gammerman A, Shafer G (2005) Algorithmic Learning in a Random World. New York, USA: Springer.
- 25. Nouretdinov I, Costafreda SG, Gammerman A, Chervonenkis A, Vovk V, et al. (2011) Machine learning classification with confidence: Application of transductive conformal predictors to MRI-based diagnostic and prognostic markers in depression. Neuroimage 56: 809–813. [DOI] [PubMed] [Google Scholar]
- 26. Wang H, Lin C, Yang F, Zhuang J (2009) An online Algorithm with confidence for Real-Time Fault Detection. Journal of Information and Computational Science 6: 305–301. [Google Scholar]
- 27.Fedorova V, Gammerman A, Nouretdinov I, Vovk V (2012) Plug-in martingales for testing exchangeability on-line. Proceedings of 29th International Conference on Machine Learning, Edinburg, Scotland.
- 28. Breiman L (2001) Random forests. Machine Learning 45: 5–32. [Google Scholar]
- 29. Duan YX, Wang YQ, Fu JJ, Xu CX (2010) The Using of Multiple Corresponding Analysis in Correlation Analysis of big Sample Categorical Variable in TCM. Journal of Mathematical Medicine 23: 65–66. [Google Scholar]
- 30. Song YM (2011) Analysis on and Current Situation of the Use by Categorical Identification in Terms of Causes of TCM Injections. Chinese Archives of Traditional Chinese Medicine 8: 072. [Google Scholar]
- 31. Hong YZ, Zhou CL, Zhou ZF, Xu JT (2009) Study on TCM syndromes of Chronic Fatigue Patients. Journal of Traditional Chinese Medicine 50: 1114–1116. [Google Scholar]
- 32.Vovk V, Gammerman A, Shafer G (2005) Algorithmic Learning in a Random World. New York, NY, USA: Springer.
- 33. Shafer G, Vovk V (2008) A tutorial on conformal prediction. Journal of Machine Learning Research 9: 371–421. [Google Scholar]
- 34. Vovk V (2006) Well-calibrated predictions from on-line compression models. Theoretical Computer Science 364: 10–26. [Google Scholar]
- 35. Vanderlooy S, Maaten L, Sprinkhuizen I (2007) Off-line learning with transductive confidence machines: an empirical evaluation. Proceedings of the 5th International Conference on Machine Learning and Data Mining in Pattern Recognition, Leipzig, Germany, Springer 2007: 310–323. [Google Scholar]
- 36. Wang HZ, Lin CD, Yang F, Hu XQ (2009) Hedged predictions for traditional Chinese chronic gastritis diagnosis with confidence machine. Computers in Biology and Medicine 39: 425–432. [DOI] [PubMed] [Google Scholar]
- 37. Yang F, Wang HZ, Mi H, Lin Cd, Cai WW (2009) Using random forest for reliable classification and cost-sensitive learning for medical diagnosis. BMC Bioinformatics S1: 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Schapire RE, Singer Y (2000) BoosTexter: A boosting-based system for text categorization. Machine Learning 39: 135–168. [Google Scholar]
- 39. Boutell M, Luo J, Shen X, Brown C (2004) Learning multi-label scene classification. Pattern Recognition 37: 1757–1771. [Google Scholar]
- 40.Wang J, Zhao Y, Wu X, Hua X (2008) Transductive multi-label learning for video concept detection. Proceedings of the 1st ACM international conference on Multimedia information retrieval. 298–304.
- 41. Wang X, Li GZ (2012) A Multi-Label Predictor for Identifying the Subcellular Locations of Singleplex and Multiplex Eukaryotic Proteins. Plos One 7: e36317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Mei S (2012) Multi-label multi-kernel transfer learning for human protein subcellular localization. Plos One 7: e37716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Elisseeff A, Weston J (2001) A kernel method for multi-labelled classification. NIPS 14: 681–687. [Google Scholar]
- 44. Zhang ML, Zhou ZH (2005) A k-nearest neighbor based algorithm for multi-label classification. IEEE International Conference on Granular Computing 2: 718–721. [Google Scholar]
- 45.Vovk V (2012) Inductive conformal predictors in the batch mode. arXiv preprint: 12092673.
- 46. Vovk V (2013) Conditional validity of inductive conformal predictors. Machine Learning 92: 349–376. [Google Scholar]
- 47. Pillai I, Fumera G, Roli F (2013) Threshold optimisation for multi-label classifiers. Pattern Recognition 45: 2055–2065. [Google Scholar]
- 48.Liu GP, Yan JJ, Wang YQ, Fu JJ, Xu ZX, et al. (2012) Application of multilabel learning using the relevant feature for each label in chronic gastritis syndrome diagnosis. Evidence-Based Complementary and Alternative Medicine 2012. doi:10.1155/2012/135387.
- 49. Wang YQ, Yan HX, Guo R, Li FF, Xia CM, et al. (2011) Study on intelligent syndrome differentiation in Traditional Chinese Medicine based on multiple information fusion methods. International Journal of Data Mining and Bioinformatics 5: 369–382. [DOI] [PubMed] [Google Scholar]
- 50. Li F, Zhao C, Xia Z, Wang Y, Zhou X, et al. (2012) Computer-assisted lip diagnosis on traditional Chinese medicine using multi-class support vector machines. BMC complementary and alternative medicine 12: 127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Yang Y (2001) A study of thresholding strategies for text categorization. Proceedings of the 24th annual international ACM SIGIR conference on Research and development in information retrieval 2001: 137–145. [Google Scholar]
- 52. Pillai I, Fumera G, Roli F (2013) Threshold optimisation for multi-label classifiers. Pattern Recognition 46: 2055–2065. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
R code of CP-RF for Multi-Label Learning.
(R)
Inclusion criteria of the patients, Diagnosis criteria, Exclusion criteria, Data Collection, Data Description of the Chronic Fatigue dataset used in this study.
(DOCX)
The Chronic Fatigue dataset used in this study. 736 patients construct the CF dataset and each case is described by 95 symptoms (features) and a subset of the four syndrome factors (labels).
(TXT)