Table 1. Normalized Tension and Pressure Errors. The RMS errors in the inferred tensions 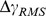and pressures 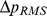have been normalized to the mean ground truth tension 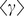and RMS ground truth pressure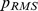, respectively, and reported as a percentage.

	No Noise		Noise 1		Noise 2		Noise 5
Method
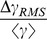
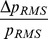
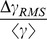
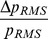
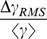
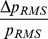
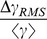
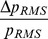
CellFIT – polyarcs	0.7	12.5	3.5±0.7	13.1±0.9	6.8±1.3	14.6±2.1	17.3±3.5	23.5±5.2
CellFIT – polyarcs, short edges removed	0.1	0.3	3.7±0.7	4.3±0.9	7.3±1.3	8.8±2.1	19.6±4.2	24.7±8.2
CellFIT – angles from closest segment	7.4	13.4	8.1±0.5	13.7±0.9	9.9±1.0	14.9±1.8	18.1±2.8	22.9±4.6
CellFIT – angles from minimal polygons	27.1	25.0	27.3±0.5	25.0±0.9	27.9±1.0	25.9±1.8	31.7±2.5	31.1±4.6
Bayesian – minimal polygons	23.8	92.9	24.1±0.4	94.0±1.5	25.1±0.4	98.0±1.9	26.5±0.4	102±3.0

For CellFIT noise analyses, Gaussian-distributed errors of the specified RMS magnitude were introduced into the limiting edge angles and edge curvatures before application of Equations 7 and 12. Noise of level x corresponds to introduced RMS angular errors of x degrees and curvature errors of x percent of the true values. For noise analysis of Bayesian force inference, which treats cells as minimal polygons, Gaussian-distributed errors were added to the triple-junction coordinates. The RMS magnitude of these coordinate errors was chosen to yield RMS angular errors of x degrees. Because introduced tension and pressure errors can produce different outcomes from one run to the next, 100 runs were carried out for each noise level using different random seeds. The statistical properties of those ensembles are reported.