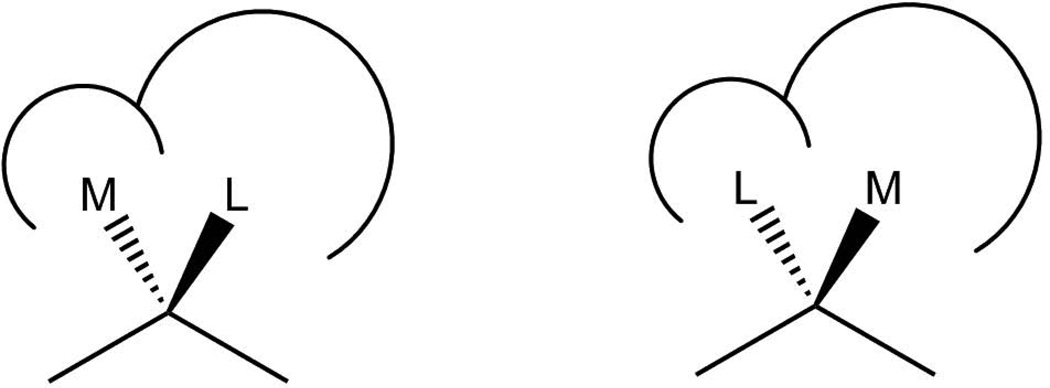Validating computer simulations of enantioselective catalysis; Reproducing the large steric and entropic contributions in Candida Antarctica lipase B

Abstract

The prospect for computer aided refinement of stereoselective enzymes is further validated by simulating the ester hydrolysis by the wild type and mutants of CalB, focusing on the challenge of dealing with strong steric effects and entropic contributions. This was done using the empirical valence bond (EVB) method in a quantitative screening of the enantioselectivity, considering both k_cat and k_cat/K_M of the R and S stereoisomers. Although the simulations require very extensive sampling for convergence they give encouraging results and major validation, indicating that our approach offers a powerful tool for computer aided design of enantioselective enzymes. This is particularly true in cases with large changes in steric effects where alternative approaches may have difficulties in capturing the interplay between steric clashes with the reacting substrate and protein flexibility.

I. Introduction

Optimizing enzymes to catalyze selective enantioselective reactions has a major potential in biotechnology.¹ For example, the use of biocatalysts for efficient synthesis of enantiomerically pure chiral molecules is of great importance in the production of drugs by the pharmaceutical industry.² Unfortunately, quantifying the observed enantioselectivity in different enzymes presents a significant challenge for approaches aimed at understanding enzyme catalysis. Experimental studies of enantioselective enzymatic reactions have provided major advances in recent years (e.g., ref^3–5). The main focus of these studies turned to lipases^3,6–13 via an examination of esterification reactions¹⁴, solvent effects¹⁵, the temperature effects⁷ and substrate effects^8–10. Furthermore, instructive advances have been done with directed evolution experiments.^3,11

Enantioselective enzymatic reactions have also been examined by theoretical approaches, including MM, MD studies^9,13,14,16 and QM/MM¹⁷, but these interesting studies have not provided quantitative insight. Attempts to use the cluster QM model^18,19 have provided interesting insight and encouraging results but such an approach might find difficulties in capturing entropic effects and in overestimating strong steric effects.

Overall it is important to explore QM/MM approaches that involve extensive sampling and evaluate the actual activation free energies, since such strategies should be able to explore entropic effects and to allow for exploring more realistic relaxation of the active site.

In trying to obtain more quantitative results it is crucial to improve two aspects of the modeling; namely the potential surface and the sampling. That is, trying to evaluate the free energy of mutating the R to S enantiomers using a force field model of their TS can be useful, but here it is important to determine the correct charge distributions and structure of the TS and this can be best done by a QM/MM approach (it is important to capture the change of the TS charge and geometry upon interaction with the entire enzyme while considering its flexibility consistently). Unfortunately, the use of a QM/MM approach is unlikely to give reliable free energies without extensive sampling (in fact, the sampling of the enzyme substrate configurations is also the most crucial requirement in classical force field studies). Here, the empirical valence bond (EVB)^20,21 arguably provides the optimal current strategy, since it combines a reliable semiempirical QM/MM model with the ability for extremely effective sampling. In fact a previous study of enantioselectivity of Candida Antarctica lipase A (CalA) by the EVB approach²² provided encouraging results. However, further general validation is still needed. Here we focus on the catalysis of the enzyme Candida antarctica lipase B (CalB)²³ which is used heavily in industrial organic synthesis by exhibiting unprecedented enantioselectivity towards (R)-phenylethanole⁷. Interestingly, this peculiar behavior is being reversed to favor (S)-phenylethanole upon mutating the active site tryptophan into the smaller alanine residue⁷. More specifically ,the apparent kinetic rate constant and the apparent Michaelis constant, i.e. $k_{\mathit{\text{cat}}}^{\mathit{\text{app}}}$ and $K_M^{\mathit{\text{app}}}$, for the wild-type (WT) CalB and the W104A mutation, were determined for the acylation of S-phenylethanole with vinyl-butanoate in cyclohexane at 30°C. The experimental results indicate a change in enantioselectivity by a factor of 8300000 through the point-mutation in the stereoselectivity pocket, which was mainly achieved by increasing $k_{\mathit{\text{cat}}}^{\mathit{\text{app}}}$ towards the slow-reacting S-configured enantiomer. More specifically, $k_{\mathit{\text{cat}}}^{\mathit{\text{app}}}$ towards S-phenylethanole was 64000 times larger for the mutant compared to WT CalB, while the same constant decreased by a factor of 130 toward the R-enantiomer. Interestingly, $K_M^{\mathit{\text{app}}}$ remained basically unchanged for the W104A mutation and was almost equal towards the R and S enantiomers, while they both decreased by a factor of two compared to the wild type. Hence, the catalysis lies equally in k_cat and K_M, and the corresponding activation barriers are given in Table I. These particular experimental results for the WT are of great interest for computer simulations, as the experimentally measurable quantities in such a highly enantioselective systems clearly meet any sensitivity that may be obtained by experimental techniques, especially for the slow-reacting enantiomer, while computer simulation do, in fact, not suffer from this limitation hence may support and refine the experiment.

Table I.

The observed activation free energies for WT CalB and its W104A mutant (MUT) ^(a)

Type-Substrate	Δgcat,exp
WT-R	13.8
WT-S	22.1
MUT-R	16.7
MUT-S	15.5

^(a)Energies are given in kcal/mol obtained from the observed rate constants¹ using transition state theory.

Further experimental analysis explored the entropic and enthalpic contributions to the enantioselectivity in the W104A mutant⁷. Very large entropic contributions (−T ΔS of 5.0, 8.1 and 8.4 kcal/mol in CH₃CN, Decaline and Cyclohexane) were found, indicating that the origin of the selectivity can be quite complex.

The rationale for the above change in enantioselectivity has been related to the extension of the size of the so-called stereoselectivity pocket²⁴ (as will be discussed in detail in section IV.2 and IV.4), leading to the high enantioselectivity for the R-enantiomer seen for the WT, while the W104A mutant shows a moderate selectivity for the S-enantiomer. However, determining the actual origin of the free energy changes that are involved in the steric effect is a major challenge. A similar challenge is associated with the analysis of the observed entropic contribution. These computational and fundamental challenges are met in the present work.

II. Background

II.1 The Catalytic Reaction

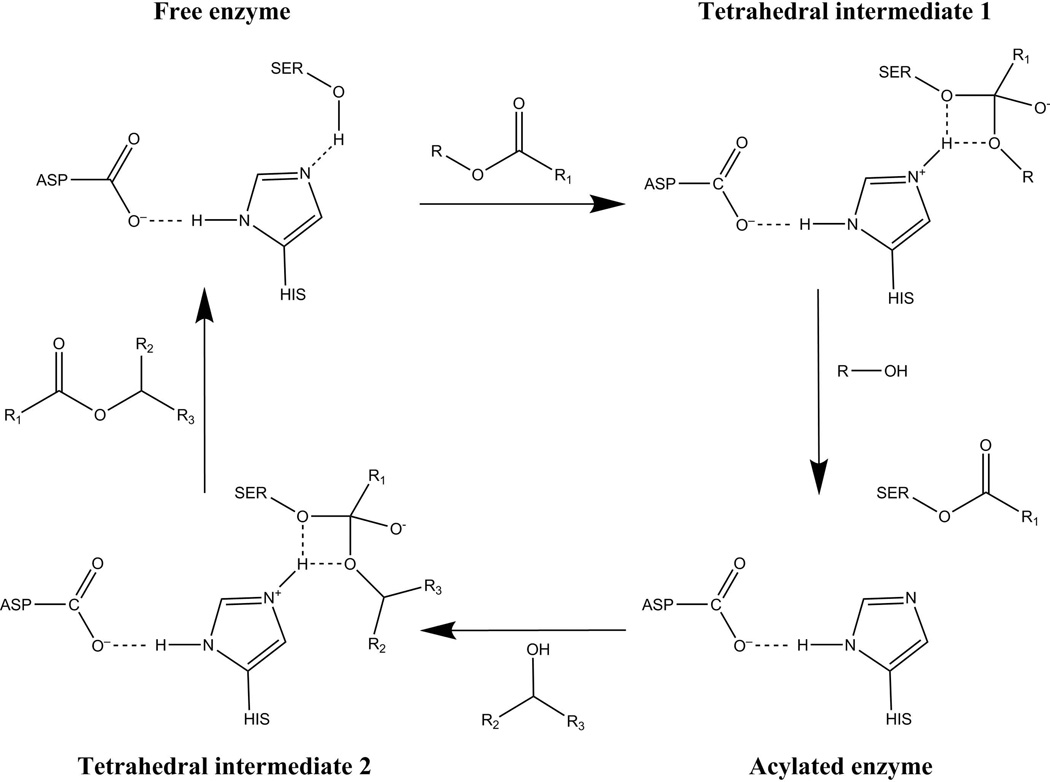
CalB is a serine hydrolase^25,26 whose catalytic mechanism has been studied extensively (for e.g.,^{2,6–10,13–17,24,27–39}). The CalB active site includes the catalytic triad of SER-HIS-ASP, which acts in the same way as the well-studied serine proteases^21,40,41 where a proton transfer from serine is followed by a nucleophilic attack of the ester carbonyl by the deprotonated alcohol (see Figure 1). The enzyme catalyzes the reaction by stabilizing the negatively charged oxyanion by an oxyanion hole (the same type of oxyanion hole is a key catalytic factor in various proteases^40,41) and by the electrostatic interaction between Asp187 and the ionized His224 (again in analogy with serine proteases^21,42).

Figure 1.

A schematic of the acylation/deacylation reaction catalyzed by CalB. The reaction is initiated by the acylation step – “Free enzyme” to “Acylated enzyme” in the scheme – leading to the acylation of the active-site serine residue. The subsequent de-acylation - from the previously obtained “Acylated enzyme” to “Free enzyme” in the scheme – is established by the secondary alcohol substrate which finally results in the release of the esterified alcohol, while the “Free enzyme” in the scheme is being recovered.

The reaction can be rate limiting by either the acylation or the deacylation steps^7,11 and in the case of transesterifications of secondary alcohols by CalB studied here, the deacylation step is rate limiting.^11,32 That is, after the serine has been acylated (the steps leading to the “acylated enzyme” in Figure 1), the reaction proceeds via a proton transfer from the secondary alcohol to the HIS residue, followed by the rate-limiting nucleophilic attack of the acylated-seryl ester leading to the observed transesterification - the production of the chiral alcohol protected by the acyl-group (the steps leading to the esterified secondary alcohol and the recovery of “Free enzyme” in Figure 1).

While there is controversy on whether the deacylation in this reaction may proceed via a stepwise or a concerted mechanism, the catalytic effects in both mechanisms are expected to be very similar.⁴³ However, the stepwise calculations require the reaction to be distilled into a proton transfer step as well as a nucleophilic attack. These are given in detail in Figures 2 and 3 for the proton transfer and the nucleophilic attack, respectively, and simulation details are given in section III.

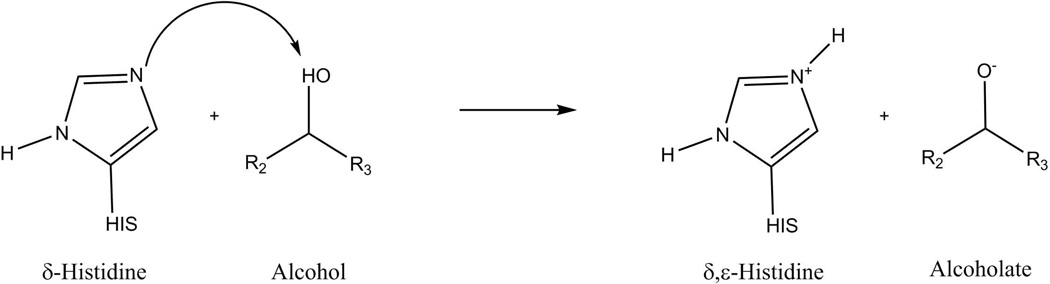
Figure 2.

Describing the proton abstraction by the imidazole base as part of the stepwise mechanism. The resulting intermediate products are doubly protonated HIS, i.e.δ,ε-Histidine, and the alcoholate nucleophile.

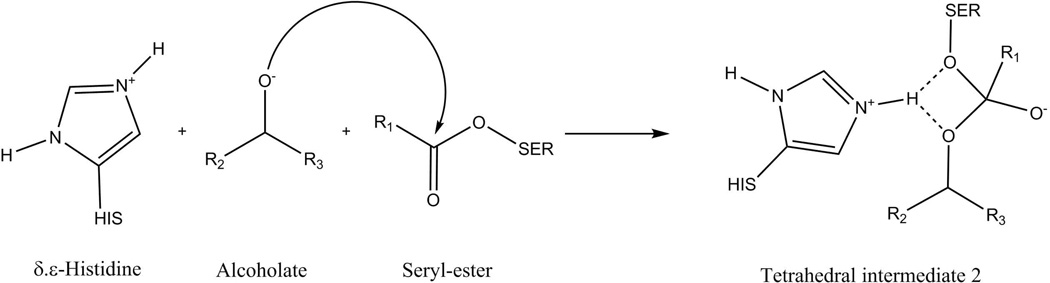
Figure 3.

Describing the nucleophilic attack of the secondary alcoholate as part of the stepwise mechanism. The breakdown of the product “Tetrahedral intermediate 2” yields the desired acylated secondary alcohol.

II.2 Defining the Selectivity

Here we explore the enantioselectivity (E), defined by:

$$E(\mathit{\text{fast}})=\frac{{(k_{\mathit{\text{cat}}}/K_M)}_{\mathit{\text{fast}}}}{{(k_{\mathit{\text{cat}}}/K_M)}_{\mathit{\text{slow}}}}$$ (1)

where the notation “fast” stands for the enantiomer with the larger k_cat/K_M. The free energies that are relevant to k_cat/K_M (or more precisely to $\frac{k_{\mathit{\text{cat}}}}{K_{\mathit{\text{bind}}}(RS)}$) can be expressed in terms of the TS binding free energy^21,44:

$$\mathrm{\Delta }{G}_{\mathit{\text{bind}}}(TS)=\mathrm{\Delta }{g}_p^{\ne }-\mathrm{\Delta }{g}_w^{\ne }\mathrm{\Delta }{G}_{\mathit{\text{bind}}}(TS)=-RT\text{ln}\left(\frac{k_{\mathit{\text{cat}}}}{K_{\mathit{\text{bind}}}(RS)}\right)+RT\text{ln}\left(\frac{k_{B}T}{h}\right)+RT\text{ln}{k}_w-RT\text{ln}\left(\frac{k_{B}T}{h}\right)\mathrm{\Delta }{G}_{\mathit{\text{bind}}}(TS)=-RT\text{ln}\left(\frac{k_{\mathit{\text{cat}}}}{K_{\mathit{\text{bind}}}(RS)}\right)+RT\text{ln}{k}_w$$ (2)

where $\mathrm{\Delta }{g}_p^{\ne }$ is the activation barrier that corresponds to $\frac{k_{\mathit{\text{cat}}}}{K_{\mathit{\text{bind}}}(RS)}$ (see ref⁴⁴).

As seen from Eq. 2, it is enough to mutate the R to S in the TS in the protein and then just to subtract the corresponding results for the mutation in water (which can be different than zero due to force field artifacts). The approach of mutating the TS has already been used in our early mutational studies⁴⁵, but at that time we mutate the protein, while here we mutate the substrate.

In the present case there is almost no difference in the selectivity observed experimentally from k_cat and from k_cat/K_M. Thus we can also explore the difference in k_cat (rather thank_cat/K_M). The contribution to the enantioselectivity in terms of k_cat will be called here E':

$$E\text{'}(\mathit{\text{fast}})=\frac{{(k_{\mathit{\text{cat}}})}_{\mathit{\text{fast}}}}{{(k_{\mathit{\text{cat}}})}_{\mathit{\text{slow}}}}$$ (3)

where

$$\text{ln}\left(\frac{{(k_{\mathit{\text{cat}}})}_{\mathit{\text{fast}}}}{{(k_{\mathit{\text{cat}}})}_{\mathit{\text{slow}}}}\right)=\mathrm{\Delta }{g}_{\mathit{\text{fast}}}^{\ne }-\mathrm{\Delta }{g}_{\mathit{\text{slow}}}^{\ne }$$ (4)

In this work we will explore the selectivity by both strategies.

III. Computational Methods

The calculation of the activation free energies was performed by the empirical valence bond (EVB) method. This method that has been described extensively elsewhere^20,21 is an empirical quantum mechanics/molecular mechanics (QM/MM) method^46–49 that can be considered as a mixture of diabatic states describing the reactant(s), intermediate(s) and product(s) in a way that retains the correct change in structure and charge distribution along the reaction coordinate. The EVB diabatic states provide an effective way for evaluating the reaction free energy surface by using them for driving the system from the reactants to the product states in a free energy perturbation umbrella sampling procedure. The reason for the remarkable reliability of the EVB is, that it is calibrated on the reference solution reaction and then the calculations in the enzyme active site reflect (consistently) only the change of the environment²¹, exploiting the fact that the reacting system is the same in enzyme and solution. Thus, the EVB approach is calibrated only once in a study of a given type of enzymatic reaction.

The EVB for the present reaction has been constructed by using the three states described in Figure S1 (see supporting information). The EVB parameters for the surfaces of the solution reaction were calibrated by using the available experimental information about this reaction (see later in this section) and were kept unchanged for the generation of the protein EVB surface (see Tables S1 to S8 in the supporting information for detailed parameters, gas-phase shifts and off-diagonal elements).

The EVB calculations were carried out by the MOLARIS package⁵⁰ using the ENZYMIX force field⁵¹. The EVB activation barriers were calculated at the configurations selected by the same free energy perturbation umbrella sampling (FEP/US) approach used in all our studies (e.g.^21,52). The simulation systems were solvated by the surface constrained all atom solvent (SCAAS) model⁵¹ using a water sphere of 20 Å radius centered on the substrate and surrounded by a 2 Å grid of Langevin dipoles and then by a bulk solvent, while long-range electrostatic effects were treated by the local reaction field (LRF) method.⁵¹ The EVB region included the secondary alcohol substrate; the imidazole ring of HIS 224 and the entire side chain of Butanoyl-serine (see Figure S1 in the supporting information). Validation studies were done within 22 Å radius of inner sphere, where we repeated the calculations of the activation barrier and obtained practically the same results (treating the distanced ionized groups with a high dielectric macroscopic model). The FEP mapping procedure involved the use of 21 frames (5 ps each) for moving along the reaction coordinate and all the simulations were done at 300 K with a time step of 1fs.

In performing the calculations we found it useful to start with restraints and then to evaluate the free energy of releasing the restraints. The rational for this strategy is discussed and justified in section IV.4. The restraints used were aimed at keeping the oxygen of the alcohol in place, combined with a restraint that allows for the alcohol to reside within clear hydrogen bonding distance to the histidine base, as well as the asymmetric carbon atom of Butanoyl-serine.

While several sets of constraints were identified, all of which resulted in very similar free energy estimates, they also seemed to heavily affect the stability of the reaction throughout the simulation as small force constants were applied. The relation to the strong steric effects seen in CalB^{6,7,10,14,35,37,38} may well translate in seemingly “unconverged” or confined simulations, as more force is required to keep the reacting fragments in reasonable positions²⁷. Thus, strong constraints of 10 kcal/mol were applied and the results presented here made use of a positional constraint for the oxygen of the secondary alcohol as well as two distance constraints keeping the oxygen within 3 A of the Nε of the HIS base as well as the carbonyl carbon of Butanoyl-serine. The simulations were repeated 4 times in order to obtain reliable results with different initial conditions (obtained from arbitrary points of the relaxation trajectory). Furthermore, the hysteresis in the calculation was examined by thermodynamic cycle closure (see section IV.3) and the average was determined by taking in each case the difference between the calculated minimum at the reaction state (RS) and the given transition state (TS). This simulation protocol was applied to reaction steps, the proton-transfer step and the nucleophilic attack.

The starting coordinates of the unbound CalB were obtained from the Protein Data Bank (PDB)⁵³ (PDB ID 1TCA²³), while the acylated serine was modeled based on the coordinates of a covalent phosphonate inhibitor (PDB ID 1LBS²⁴). The same approach was used to model the mutant by simply mutating the tryptophan residue into an alanine using MOLARIS⁵⁰. During system preparation, all crystal waters were removed while a structural water in clear hydrogen bonding distance to ASP187 was preserved (residue HOH 406 from the coordinates of PDB 1TCA²³); all hydrogen atoms and all other water molecules were added using MOLARIS^50,51 and the catalytic ASP187 was deprotonated in all simulations presented leading to a formal net charge of -1 for the protein (and not including the different states of the catalytically active HIS224).

The partial atomic charges for all resonance structures (see Figure S1 and Table S1 in the supporting information) were determined from the electronic wave functions by fitting the resulting electrostatic potential in the neighborhood of these molecules using the Merz-Singh-Kollman scheme.⁵⁴ The electronic wave functions were calculated with hybrid density functional theory (DFT) using the B3LYP method^55–58 and the 6–311G** basis set^59–62, performed with the Gaussian03 package.⁶³

The generated protein complex system (that includes the protein, bound ligand, water and Langevin dipoles) was pre-equilibrated for 1ns at 300K with a time steps of 1fs using the ENZYMIX force field.^50,51 The spherical inner part of the system with radius 20Å was constrained by a weak harmonic potential of the form, $V\text{'}={\mathrm{\Sigma }}_{i}A{({\overrightarrow{r}}_i-{\overrightarrow{r}}_i^0)}^2$ with A=0.03 kcal mol⁻¹Å² to keep the protein atoms near the corresponding observed positions, along with the inner spherical constraints. The protein atoms outside this sphere were held fixed and their electrostatic effects excluded from the model.

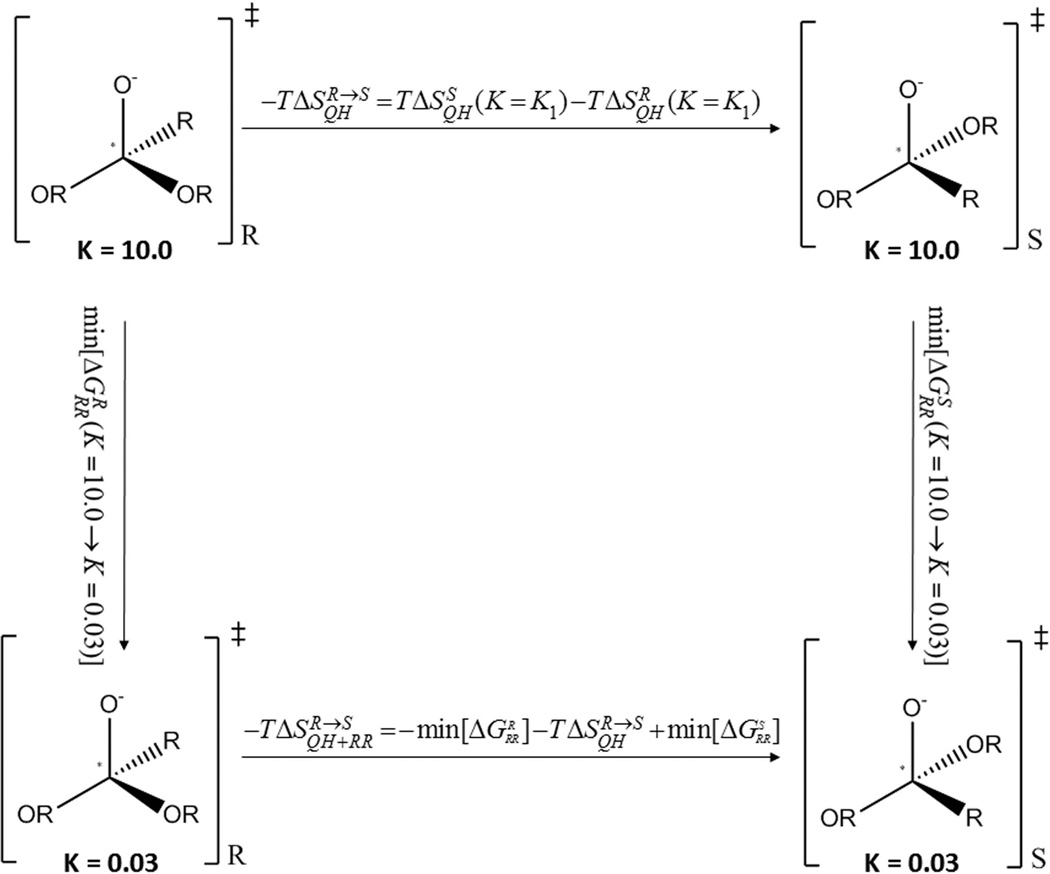
Since the present work includes a careful attempt to evaluate entropic contributions to enantioselectivity, we review here our restraint release (RR) approach for calculating entropies.^64–66 (this approach should not be confused with the strategy of running the EVB with restraints in calculating the activation free energies). Our approach involves a variation of the original RR approach where we evaluate the entropy of a state with a potential U_A, we start by adding to the potential of each state a strong harmonic constraint (with a force constant K set at 10.0 kcal⁻¹ A⁻²) centered at a position, R̅, near the minimum of that potential. With a strong constraint we can evaluate the entropy of the system by the widely used quasi harmonic (QH) method⁶⁷ (which is very problematic with realistic shallow potentials). Next we evaluate the entropy on the real potential by moving from the restraint potential to the real potential by releasing the strong restraint, K, and evaluating the corresponding free energy, ΔG_RR. Here we use our finding that ΔG_RR depends on the position of R̅, but the lowest ΔG_RR obtained by changing R̅ includes only entropy and no enthalpic contributions (as was established in most details in⁶⁴). Thus we can write

$$-T\mathrm{\Delta }S(U_A)=-T\mathrm{\Delta }{S}_{QH}(U_A+U_{\mathit{\text{rest}}}^N(K=K_1))+\text{min}[\mathrm{\Delta }{G}_{RR}(K=K_1\to K=0)]$$ (5)

where ΔG_RR designated the RR obtained by changing the indicated force constants and indicates the minimum value of the indicated ΔG_RR from a set of different restraint coordinates (R̅). More specifically we apply a Cartesian restraint:

$$U_{\mathit{\text{rest}},j}^N=\left(\frac{K_j}{2}\right)\sum _i{(R_i^N-{\mathrm{R̅}}_i^N)}^2$$ (6)

where i runs over the relevant coordinates (in the present case the solute coordinates $R_i^N$) and ${\mathrm{R̅}}_i^N$ are reference coordinates that define the minimum of the restraining potential at the given state (e.g. N = I or N = II for the TS of the R and S-enantiomer respectively). Using this restraint we evaluate the QH entropy contribution, −T ΔS(K)_OH for the energy of the system plus the restraint. We then evaluate the free energy of releasing the restraint using a standard FEP procedure with a mapping potential of the form

$$U_m^N=(1-{\lambda }_m)U_{\mathit{\text{rest}},1}^N(K_1)+{\lambda }_m{U}_{\mathit{\text{rest}},2}^N(K_2)+E$$ (7)

where E designates the unconstrained potential surface of the system and where λ_m is changed gradually from 0 to 1. Finally the relevant entropy is evaluated by Eq. 5. The calculations follow the simulation conditions of our EVB protocol with an 18 Å simulation sphere of explicit water molecules subject to the surface-constrained all-atom solvent boundary conditions. However, the RR-FEP involved the release of the position restraints between 48 windows, each with a simulation time of 40 ps at 300 K and a 1 fs time step.

IV. Results and Discussion

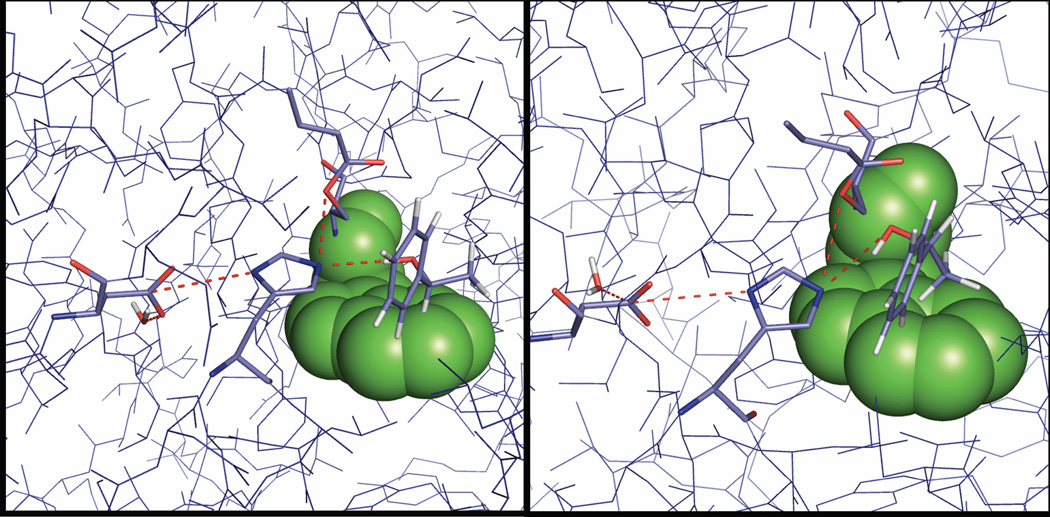
Our task is to quantify the energetics of the reaction for the R- and S-configured substrates in CalB where the modeled binding modes for the enantiomers are shown in Figure 4 (and will also be discussed in subsequent sections). With this initial structure we can calculate the relevant activation barriers as described below.

Figure 4.

A model of the RS shown after 1 ns equilibration for the R-enantiomer (left) and the S-enantiomer (right) (from the coordinates of PDB ID 1TCA²³). The protein is shown in blue line representation with potential hydrogen bonds indicated by red dashed lines; the catalytic triad, together with phenylethanole and the preserved water molecule are shown in stick representation using light blue, navy and red for carbon, nitrogen and oxygen atoms, while TRP 104 acting as the proposed stereoselectivity pocket is shown in sphere representation using green. Hydrogens have been omitted for clarity and are only shown for the substrate as well as the preserved water molecule. The model was created using PyMol.⁸¹

IV. 1 Obtaining the EVB Surfaces for the Catalytic Reaction

Our study started with a systematic analysis of the reference reaction for histidine assisted ester hydrolysis in solution, using the relevant experimental information.²¹ The calibration procedure includes the energetics of the proton transfer (PT) from phenylethanole to imidazole and the energetics of the following nucleophilic attack (NA) of the ionized alcoholate and carbonyl carbon of butanoyl-serine (see ref⁷ and Figures 2 and 3).

As mentioned above, we start with the stepwise paths, separating the proton transfer and nucleophilic attack steps^17,43. The energy of the proton transfer step (Figure 2) in water is determined from the pK_a values (pK_a (Phenylethanole) ~ 14.4 and pK_a (His) ~7²¹) and is found to be 10.1 kcal/mol.

The energy of forming the tetrahedral intermediate was calibrated by using the rate constant adapted from a similar uncatalyzed reaction. More specifically, we have considered the hydrolysis reaction of the hydroxide ion with methyl-isobutyrate and methyl-isopropionate - 18.6 and 18.9 kcal/mol respectively.⁶⁸ While there is a common scaffold for these substrates to butanoyl-serine, our nucleophile is a secondary alcohol instead of the hydroxide ion. Here, an energetic difference of up to 4 kcal/mol of the activation barrier of alcoholate versus hydroxide was previously established on formamide esterification with specific hindsight on serine hydrolases.⁴³ Combined with experimental and computational studies on similar substrates, all of which point towards an activation free energy between 15 and 19 kcal/mol^32,68,69, we are confident in assuming a similar reduction for our specific reaction, which has subsequently been set at 15 kcal/mol for fitting the EVB solution surface.

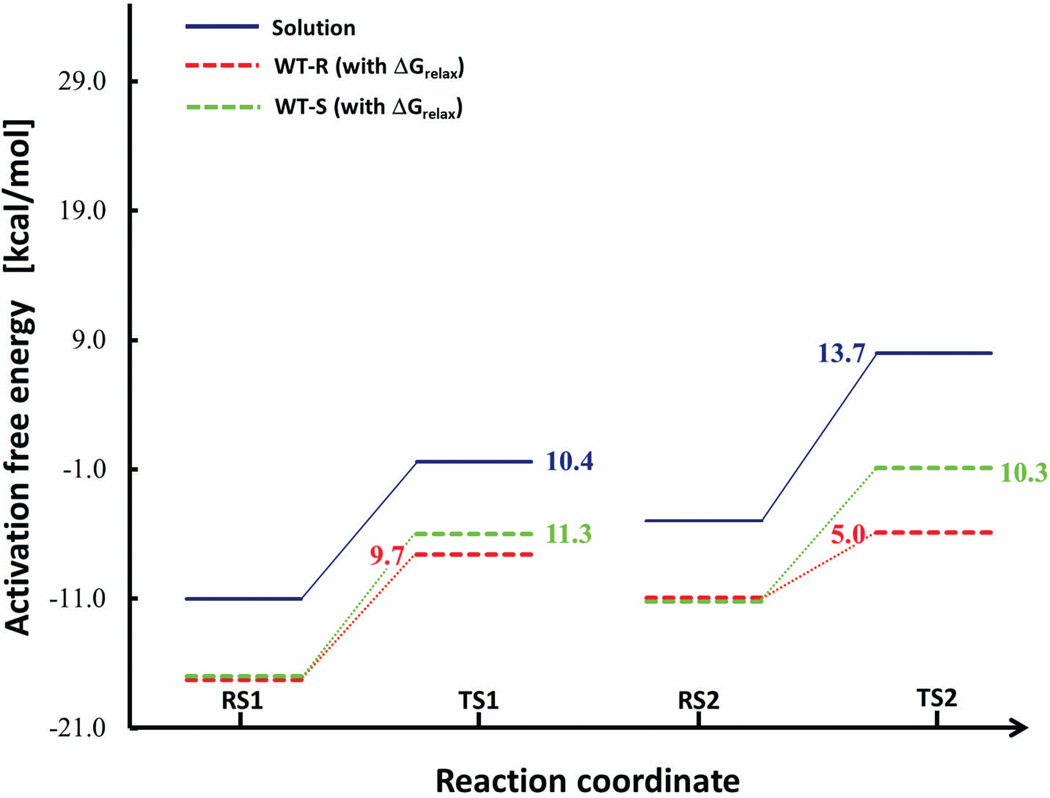
Combining the free energy for the PT step and the nucleophilic attack gives a total activation barrier ($\mathrm{\Delta }{G}_{\mathit{\text{cage}}}^{\ne }$) of ~25.1 kcal/mol for our reference reaction in the solvent cage. The barrier for a concerted path is expected to be very similar to our stepwise estimate (see ref^17,43). The above estimate was used to calibrate the EVB surface for our reference reaction in solution and the corresponding free energy reference surfaces for the solution and the wild-type enzyme are shown in Figure 5. The results reported in the figure were obtained by a specialized restraint approach that will be discussed in section IV.4

Figure 5.

Diagram of the calculated activation barriers (in kcal/mol) for the transesterification using the EVB method. Here the final barriers are given that include in case of the enzyme the free energy of removing the restraints (not for the solution). The results reported in the figure were obtained by the specialized restraint relaxation approach that will be discussed in section IV.4

Using the EVB parameters calibrated on the reference solution reaction we evaluate the EVB free energy surface for the reaction in CalB. The resulting free energy calculations for each independent run are given in Tables II and III and IV for the results in solution, WT enzyme and mutant respectively. The final activation free energy estimates compared to experiment are summarized in Table V. As seen from Table V, we obtained a calculated activation barrier, Δg_cat,calc, of 14.7 kcal/mol for the R-enantiomer and a barrier of 21.6 kcal/mol for the S-enantiomer. For completeness longer simulations were performed by extending the total runtime per frame three-fold and gave 15.3 kcal/mol for the R-enantiomer, hence lying within the statistical error of the method. Overall these barriers for the chemical reaction are in satisfying agreement with the observed barriers (Δg_cat,exp=13.8 kcal/mol for the R-enantiomer and 22.1 for the S-enantiomer obtained using transition state theory respectively), and the observed k_cat of the wild type CalB for the enantiomers.⁷

Table II.

Calculated activation free energies (in kcal/mol) for the reaction in solution (Sol) for four runs ^(b)

Run	ΔGPT (Sol)	ΔGNA (Sol)	Δgcat,calc (Sol)
run1	10.1	13.5	23.6
run2	11.7	14.6	26.3
run3	9.8	12.9	22.7
run4	10.3	13.6	23.9
AVG	10.4	13.7	24.1
SD	0.8	0.7	1.5
MUE	0.4	0.4	0.8

^(b)given by ΔG_PT (Sol), ΔG_NA (Sol) and Δg_cat,calc (Sol) for the individual barriers of the PT and NA and the total calculated barrier respectively. Statistical figures of merit are given by the average (AVG), standard deviation (SD) and the mean unsigned error (MUE).

Table III.

Calculated activation free energies (in kcal/mol) for the reaction in the WT for four runs ^(c)

Run	ΔGPT WT-R	ΔGNA WT-R	Δgcat,calc,relax WT-R	ΔGPT WT-S	ΔGNA WT-S	Δgcat,calc,relax WT-S	ΔΔgcat,calc,relax(a) WT (R→S)
1	9.2	4.4	13.6	11.2	11.9	23.1	9.5
2	10.7	4.9	15.6	13.3	9.3	22.6	7.0
3	9.9	5.6	15.5	10.0	9.2	19.2	3.7
4	9.1	5.1	14.2	10.7	10.6	21.3	7.1
AVE	9.7	5.0	14.7	11.3	10.3	21.6	6.8
SD	0.4	0.7	1.0	1.4	1.0	2.5	2.4
MUE	0.2	0.3	0.5	0.7	0.5	1.2	1.2

^(c)The individual contributions ΔG_PT and ΔG_NA for each reaction and enantiomer provide the total barriers given by Δg_{cat,calc,relax}. The absolute difference in activation free energies between the enantiomers was calculated with the free energy of releasing the geometrical restraints and is labelled ΔΔg_{cat,cal,relax}. Statistical figures of merit are given by the average (AVG), standard deviation (SD) and the mean unsigned error (MUE).

Table IV.

Calculated activation free energies (in kcal/mol) for the reaction in the MUT for four runs ^(d)

Run	ΔGPT MUT-R	ΔGNA MUT-R	Δgcat,calc MUT-R	ΔGPT MUT-S	ΔGNA MUT-S	Δgcat,calc MUT-S	ΔΔgcat,calc MUT (R→S)
1	10.7	6.9	17.6	10.1	5.8	15.9	−1.7
2	12.4	5.8	18.2	10.3	4.5	14.8	−3.4
3	10.8	7.6	18.4	11.4	5.3	16.7	−1.7
4	11.7	6.1	17.8	10.9	4.5	15.4	−2.4
AVE	11.4	6.6	18.0	10.7	5.0	15.7	−2.3
SD	0.8	0.8	0.4	0.6	1.1	0.8	0.8
MUE	0.4	0.4	0.2	0.3	0.6	0.4	0.4

^(d)The individual contribution ΔG_PT and ΔG_NA for each reaction and enantiomer provide the total barriers given by Δg_cat,calc. The absolute difference in activation free energies between the enantiomers was calculated without the free energy of releasing the geometrical restraints and is labeled ΔΔg_cat,calc. Statistical figures of merit are given by the average (AVG), standard deviation (SD) and the mean unsigned error (MUE).

Table V.

Calculated activation free energies (in kcal/mol) for the PT and NA reactions in the WT and the MUT for each enantiomer.^(e)

System	ΔGPT	ΔGNA	Δgcat,calc(a)	Δgcat,calc,relax(b)	Δgcat,exp(c)
solution R/S	10.4	13.7	24.1	na	25.1
WT-R	9.7	5.0	14.7	16.7	13.8
WT-S	11.3	10.3	21.6	23.9	22.1
MUT-R	11.4	6.6	18.0	na	16.7
MUT-S	10.7	5.0	15.7	na	15.5

^(e)The total barriers without and with addition of the free energy of removing the geometrical restraints at the RS and TS are indicated by Δg_cat,cal and Δg_{cat,calc,Relax} respectively, and the experimental barrier is given by Δg_cat,exp. Statistical figures of merit are given by the average (AVG), standard deviation (SD) and the mean unsigned error (MUE).

IV. 2 The Binding of Secondary Alcohols to Candida Antarctica lipase B

An issue that has played an important role in the discussion of the selectivity of CalB and other enzymes is the nature of the binding modes^{6,7,10,14,24,27,28,31,35,38}. Although this issue appears to be overemphasized due to the use of approaches with limited sampling (see below), it is very useful to consider this issue here.

The empirical Kazlauskas rule⁷⁶ has been used to assess the most likely binding mode of the fast-reacting enantiomer. That is, while the rule suggests a clear preference for the (R)-enantiomer of a secondary alcohol, which seems confirmed by experiment^8,17,32, it makes modeling the (S)-enantiomer almost impossible, as its’ large phenyl ring cannot fit in the postulated stereoselectivity pocket, providing no significant conformational changes are involved, while for the R-enantiomer the large group would point towards bulk solvent. This is illustrated in Figure 6 where the binding mode on the right is termed "unproductive" as the medium-sized substituent binds in the larger stereoselectivity pocket, while the "productive" mode, shown on the left, would be able to accommodate the larger substituent and facilitate catalysis.

Figure 6.

The productive and unproductive binding modes proposed for the binding of secondary alcohols to CalB. While the binding mode shown on the left can easily accommodate both substituents, the binding mode on the right cannot accommodate the large substituent L in the postulated pocket, thus making it the slow-reacting enantiomer according to Kazlauzkas.⁷⁶

The asymmetric sp3-hybridized carbon atom binds four substituents, three of which define its absolute configuration (relative to the hydrogen in our case), which amounts, theoretically, to a total of 4 different binding modes for the S-enantiomer. According to Cahn-Ingold-Prelog^70,71, these were systematically assigned according to the weight of their substituents, thus leading to H/O, M/L and M/H permutations compared to the R-enantiomer (Here H, O, M and L refer to hydrogen, oxygen, medium-sized and large-sized substituents, see for example ref²⁸).

The interconversion between those modes during a simulation is subject to the choice of sampling, which in turn is combined with the natural confinement presented by the detailed architecture of the active site. Here, the use of restraints to maintain a particular binding mode during the simulation – or simply just a certain geometry - is a useful tool. However, as it will affect the free energies by modifying the conformational sampling, it becomes necessary to evaluate the free energy of removing the restraint(s). The effectiveness of this approach will be illustrated in section IV.4.

IV.3. Calculating the Selectivity In Terms of TS Binding energy

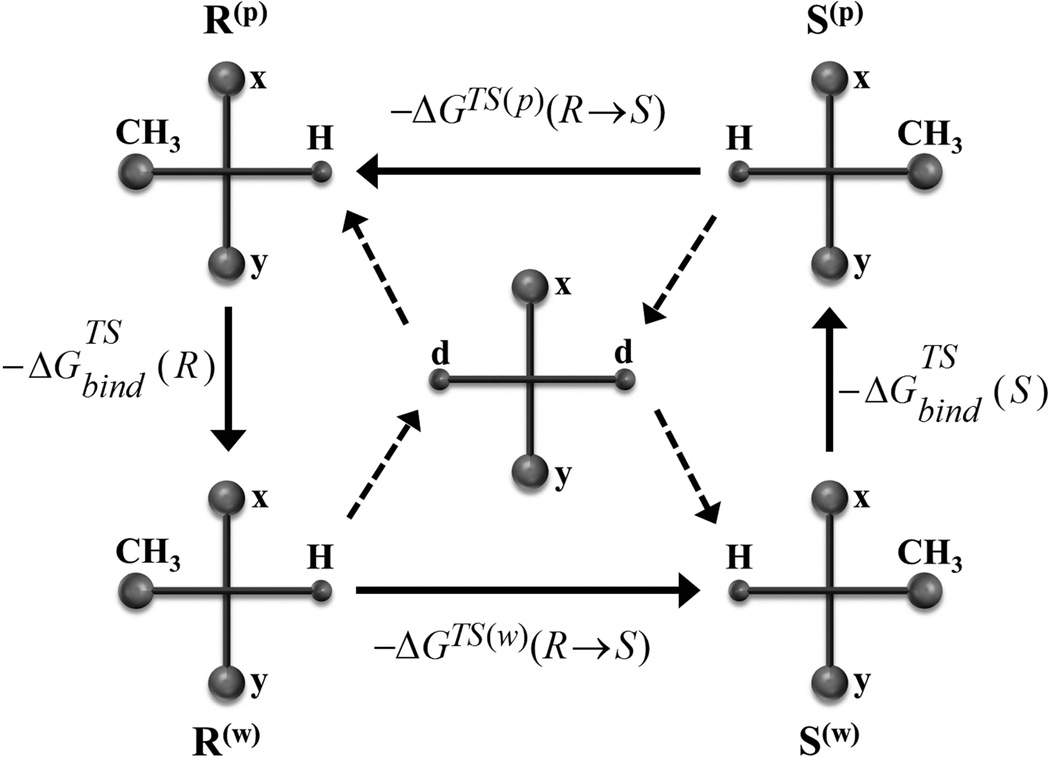
The rate-limiting step in the transesterification studied here is the second nucleophilic attack of the secondary alcoholate on the carbonyl carbon of the modified serine residue^8,17,32. Consequently, the enantioselectivity can be defined as the difference between the TS binding free energies of the R- and S enantiomer. As outlined previously²², we can use the thermodynamic cycle of Figure 7 and obtain:

$$-RT\text{ln}(E(R))=\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathit{\text{bind}}}^{TS}(R\to S)-RT\text{ln}(E(R))=\mathrm{\Delta }{G}_{\mathit{\text{bind}}}^{TS}(S)-\mathrm{\Delta }{G}_{\mathit{\text{bind}}}^{TS}(R)-RT\text{ln}(E(R))=\mathrm{\Delta }{G}^{TS(p)}(R\to S)-\mathrm{\Delta }{G}^{TS(w)}(R\to S)$$ (8)

Figure 7.

Thermodynamic cycle for the mutation of the R-enantiomer into the S-enantiomer. Here, the mutation of CH₃ to H and H to CH₃ is described schematically. As outlined in the main text, the mutation is practically done at the transition state by converting both, the CH₃ and H, to dummy atoms.

In using this expression it is enough to mutate the R to S in the TS in the protein and then just substract the corresponding results for the mutation in water (this reflects force field artifacts). The approach of mutating the TS has already been used in our early mutational studies⁷², but at that time the mutation was performed on the protein, while here we mutate the substrate. This is achieved by converting the groups that distinguish R from S to real or dummy atoms. More specifically, we mutate the dummy atoms in R to real atoms in S and the real atoms in R to dummy atoms in S.

The reaction coordinate for moving from the real TS to the dummy TS was split into 31 frames (of 5ps each) for the FEP mapping procedure and all the simulations were performed at 300K with a 1 fs time step. The structures used were taken from the corresponding EVB calculations, after a further relaxation for 800ps for each system, and each simulation was repeated 8 times in order to obtain reliable results with different initial conditions (obtained from arbitrary points along the TS relaxation trajectory). In order to avoid the end-point catastrophe in mutating dummy atoms, we found it convenient to delete the first and last frame, while exploring the convergence behavior with larger number of frames.

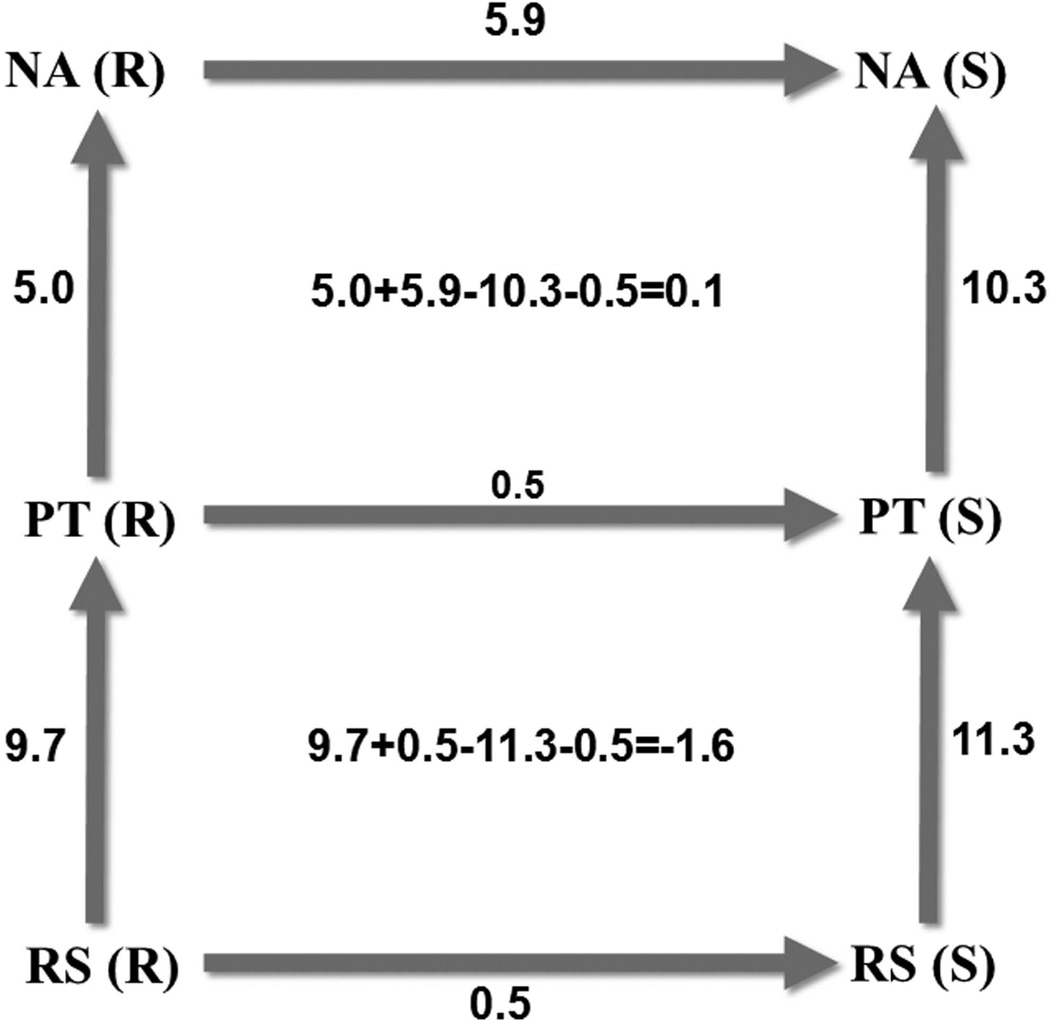
The results of these R to S mutations at the TS are summarized in Table VI. While the agreement with experiment is reasonable (the absolute error lies around 2 kcal/mol for the wild-type CalB), the results are interesting since they allow us to complete thermodynamic cycles that involve not only the rate-limiting step, but the entire chemical reaction. That is, we perform the same procedure for the PT step to calculate the binding free energy of the TS for the proton transfer, and finally calculate the energy for perturbing the atoms distinguishing R from S at the RS using our standard EVB procedure (also by perturbing the atoms distinguishing R from S to dummy atoms). While no experimental information is available for these (the experimental observation is based on the rate-limiting step) they still allow us to construct probably the first complete thermodynamic cycle over an entire chemical reaction. Overall the energies given along the cycle in Figure 8 provide a major consistency check on our approach.

Table VI.

Calculated binding free energies (in kcal/mol) of the TS^(f)

System	Selectivity	ΔΔGbind,calc(TS)	ΔΔGbind,exp(TS)
WT/PT	R	0.5±1.6	8.3
WT/NA	R	5.9±2.0
MUT/PT	R	0.5±1.3	−1.4
MUT/NA	R	3.5±2.2

^(f)ΔΔG_bind,calc (TS) is compared to experiment ΔΔG_bind,exp (TS) for the PT and the NA bound to the WT and the MUT. The preferred enantiomer is given in the column denoted by “Selectivity;” the calculated ΔΔG_bind,calc (TS) is given with the MUE over a total of 8 independent runs.

Figure 8.

Thermodynamic cycle over the entire chemical reaction. For the vertical arrows the EVB method is used to estimate the activation free energies responsible for catalysis, while the horizontal arrows stand for the mutations (to dummy atoms) aiming to calculate the binding free energies of the TS of each of the chemical reactions, i.e. for the PT as well as the NA for each enantiomer (in brackets). To be able to close the lower cycle, mutations have also been performed on the RS, but here the EVB method has been used to turn the respective atoms into dummies. The numbers in the center of each cycle indicate the observed hysteresis effects, standing at 0.1 for the NA and −1.6 for the PT. All units are in kcal/mol.

IV. 4. Obtaining Improved Result by Introducing and Removing Restraints

The involvement of large steric effects in the enantioselective recognition by CalB was found to present a significant challenge to calculations of the relevant free energies. That is, we found that running simulations form different initial conditions tends to give rather unstable results for the calculated enantioselectivity. On the other hand, performing free energy calculations with restraint and then releasing the restraint may eliminate the need for extensively long simulations. That is, calculations with restraints tend to be stable since they are confined to a well-defined region of the configurational space and the relaxation from the restraint region tends to give more stable results than those obtained by staring form arbitrary configurations in a shallow landscape.

A comparison of the calculated free energies obtained for the PT and NA run at K set to 0.03 kcal/mol would at least support the above claim. Clearly, inspection of Tables III and IV shows an expected mean unsigned error (MUE) for the final barriers well within 1.2 kcal/mol which rapidly degrades to 2.5 for the final barriers obtained with simulations run at K=0.03 kcal/mol (see Table VII). Consequently, the free energy of removing the restraint(s) allows us to estimate the “relaxation” free energies, ΔG_relax, and “relax” the final barriers accordingly. Therefore we start with the free energies of the RS and the TS of the PT and the NA obtained by our EVB simulations that were run at K set to 10.0 kcal mol⁻¹ A⁻² and then add the correction obtained upon reducing K to 0.03 over a total of 48 evenly spaced Ks. The same value was also used for K₁ in our entropy calculations. For consistency, all other MD simulation conditions detailed in section III are maintained, as were the free energies calculated using the standard FEP procedure. The underlying thermodynamic cycle for calculating Δg_{cat,calc,relax} shown in Figure S2 (supporting information) illustrates our approach and the obtained barriers for the PT and NA are given in Figure 6 for the WT (or a more detailed presentation in Figure S3 in the supporting information). Interestingly the average values of the results did not change drastically (see Table VII) but the stability of the calculations deteriorated very significantly.

Table VII.

Calculated activation free energies (in kcal/mol) for the reaction in the WT for four runs ^(g)

Run	ΔGPT WT-R	ΔGNA WT-R	ΔGPT WT-S	ΔGNA WT-S	ΔΔgcat,cal (R→S)
1	12.4	5.6	10.2	14.5	6.7
2	9.1	14.4	12.5	8.5	−2.5
3	14.1	3.5	15.4	6.5	4.3
4	9.5	4.5	5.8	17.5	9.3
AVG	11.3	7.0	10.9	11.7	4.5
SD	2.4	5.0	4.1	5.1	5.1
MUE	1.2	2.5	2.0	2.6	2.5

^(g)using K=0.03 for the geometrical constraints. The difference in individual contribution ΔG_PT and ΔG_NA for each reaction and enantiomer gives the absolute difference in activation free energies between the enantiomers, ΔΔg_cat,calc (R→S). Statistical figures of merit are given by the average (AVG), standard deviation (SD) and the mean unsigned error (MUE).

IV. 5 Exploring Entropic Contributions to Selectivity

Following the outline in the method section we conducted calculations of the entropic difference between the enantiomers at the TS. This was done using the two paths according to the cycle shown in Figure 9 and our calculated results given in Table VIII for both enantiomers bound to WT CalB.

Figure 9.

Thermodynamic cycle used to estimate the entropic contribution to catalysis for binding the TS of the enantiomers. The vertical arrows correspond to the simulations where the RR approach is used to perturb/release the restraint, the QH approximation is utilized to calculate the contribution from infinite to strong restraint (top horizontal arrow).

Table VIII.

Calculated entropies (in kcal/mol) provided by the RR and QH calculations for the NA at the TS ^(h)

WT-R (TS)	1	2	3	4
RR 10 →0.03	−35.3	−35.8	−35.9	−36.2
QH10	−29.8	−29.5	−30.0	−29.5
RR+QH	−65.1	−65.3	−65.9	−65.9
WT-S (TS)	1	2	3	4
RR10 →0.03	−35.5	−34.9	−35.2	−35.1
QH10	−28.7	−28.9	−29.4	−28.5
RR+QH	−64.2	−63.8	−64.6	−63.6
MUT-S (TS)	1	2	3	4
RR10 →0.03	−32.2	−33.5	−32.9	−32.6
QH10	−27.4	−27.9	−27.6	−27.3
RR+QH	−59.6	−61.4	−60.5	−59.9
MUT-R (TS)	1	2	3	4
RR10 →0.03	−33.5	−33.9	−34.0	−33.3
QH10	−30.8	−30.5	−31.0	−30.8
RR+QH	−64.3	−64.4	−65.0	−63.8

^(h)The table includes the results over four (1 to 4) simulations, each using different restraint coordinates. Each simulation consisted of 48 windows, over 40ps at 300K and a 1fs time step. The bold values indicate the calculated minimum, their difference reflecting the best estimate of -TΔS. As discussed in the main text, this variational minimization reflects the fact that all the RR free energies contain enthalpic contributions, which approach zero for restraint coordinates that gives the lowest RR/QH energies.

Our practical RR calculations involved the following steps: after an initial relaxation using MD runs of 1ns at 300 K with a time step of 1fs, arbitrary points along the trajectory were then collected to generate eight different sets of Rs, the constraint coordinates. The RR contributions for each of these sets were then evaluated. This was done by calculating the QH contribution with =10.0 kcal mol⁻¹A⁻² using

$$-T\mathrm{\Delta }S=-T\mathrm{\Delta }{S}^B{(K=K_1^{\text{'}})}_{QH}+\text{min}[\mathrm{\Delta }{G}_{RR}^B(K=K_1^{\text{'}}\to k=0)]+T\mathrm{\Delta }{S}^{UB}{(K=K_1^{\text{'}})}_{QH}-\text{min}[\mathrm{\Delta }{G}_{RR}^{UB}(K=K_1^{\text{'}}\to K=0)]+T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{cage}}}$$ (9)

Where ΔS^B (K = K₁)_QH designates the $\mathrm{\Delta }{S}_{QH}(U_A+U_{\mathit{\text{rest}}}^N(K=K_1))$ term of Eq. 5 for the potential B by in the presence of the constraint.

The calculated results are given in Table VIII for both enantiomers bound to the W104A mutant. The reported results were obtained by releasing the constraints on the TS of the substrates atoms while leaving the enzyme unconstraint. A more rigorous treatment should involve also a RR treatment of the active site^65,73, but it is likely that in the present case exploring the entropy of the substrate with a relaxed enzyme is a reasonably reliable option. Encouragingly, we obtained 3.5 kcal/mol difference in the entropic contribution whereas the experiment in CH₃CN, for example, lies at 5.0 (or 8.1 and 8.4 kcal/mol in decaline and cyclohexane respectively). Here, the obvious difference lies in the fact that organic media are used in the experiment, while the simulation is performed in water. Arguably, this difference in the entropic contribution may well reflect the subtle protein conformational change induced by the solvent (and temperature), which finally translates energetically to catalysis. In this case, our results would suggest that the W104A mutant of CalB is likely to share the most important conformational features between water and CH₃CN, and that the imposition of constraints on all atoms of the evb region is sufficient for estimating the entropic contribution to catalysis. Nevertheless, to quantify accurately the impact of protein flexibility and conformational states in different solvents (and with respect to the entropy at different temperatures) to catalysis, more detailed studies are required in combination with parameterization of novel solvent models for biomolecular simulations.

Finally, and as shown previously^64,73, a more rigorous treatment of the entropy ideally involves the RR on the entire active site. Here one may assume that in the particular case of CalB the entropic difference, that is the difference between the R and S enantiomer at the TS, is sufficient to provide us with an accurate estimate for the entropic contribution, and that the extension of the RR to the entire active site will not change the absolute difference between the enantiomers at the TS dramatically. However, this was not attempted in this work, as the main focus here lies on calculating the enantioselectivity on a real biological system, while the encouraging results of the entropy calculations certainly provide us with a benchmark suggesting to focus our RR approach more systems.

V. Concluding Remarks

Optimizing enzymes to catalyze selective enantioselective reactions has a major potential in biotechnology^1,74–78, including in the generation of biocatalysts for efficient synthesis of enantiomerically pure chiral molecules for the production of drugs by the pharmaceutical industry^74,79,80.

Recent advances in this field have been due in part to directed evolution experiments^{11,74–77,79,80} with some qualitative insight from theoretical studies (see Introduction). It seems to us that at the present stage it is important to push the capacity of theoretical simulation as useful tool in designing enantioselectivity enzymes. While previous studies^{9,13,16,17,27,28,31,32,36,69}, including ours²², gave encouraging results, the ability of simulations to model consistently and reliably strain effects on enantioselectivity have not been demonstrated. In fact, a recent study²⁷ of the WT CalB was forced to use a very large constraint of 100 kcal mol⁻¹ A⁻² to guarantee a hydrogen bond between the substrate and the imidazole base. Of course, using such a treatment cannot be a justifiable strategy. Similarly, energy minimization strategies are unlikely to allow proper relaxation of the protein steric forces. This does not mean that simple energy minimization, and even just visual inspection, cannot give a powerful guide for getting effective mutations. However, approaches that do not involve extensive sampling are unlikely to give stable results, just because of the fact that starting from different initial configurations gives different results. In principle one should be able to use free energy calculations, but the reliability of such strategies must be established and this has been the main focus of the present work.

The present study confirmed the suspicion that a converging prediction of enantioselectivity is a major challenge (since major sampling is needed to obtain converging results). Our results demonstrate reasonable thermodynamic cycle closure, providing us with yet more confidence and validation of our method and established formally rigorous free energy calculation of mutational effects of absolute enantioselectivity, where all the elements of the calculation involve careful sampling of what is basically a reliable semiempirical QM/MM potential over the entire chemical reaction.

In addition to the demonstration that we can capture reliably steric contributions to enantioselectivity, we also explored here our ability to evaluate the corresponding entropic effects. It appears that the RR approach coupled with the EVB offers a powerful way of accomplishing this task. Further studies should focus on the change in entropy with the change of the solvent as this remarkable effect may give interesting clues on the role of organic solvents in catalysis.

In view of the effectiveness of the present approach we hope that it can serve as a general tool for screening and refining enantioselective enzymes.