Abstract
The spin lattice (T1) and spin-spin (T2) relaxation times, along with the proton density (PD) contain almost all of the information that 1H MRI routinely uses in clinical diagnosis and research, but are seldom imaged directly. Here, three methods for directly imaging T1, T2, and PD with the least possible number of acquisitions–three, are presented. All methods utilize long 0° self-refocusing adiabatic pre-pulses instead of spin-echoes to encode the T2 information prior to a conventional gradient-echo MRI sequence. T1 information is encoded by varying the flip-angle (FA) in the ‘Dual-τ Dual-FA’ and ‘Four-FA’ methods, or the sequence repetition period, TR, in the ‘Dual-τ Dual-TR’ method. Inhomogeneity in the FA distribution and slice-selection profile are recognized as the main error sources for T1 measurements. The former is remedied by integrating an extra FA-dependent acquisition into the ‘Four-FA’ method to provide self-corrected T1, T2, PD, and FA in just four acquisitions-again, the minimum possible. Slice profile errors–which manifest as differences between 2D and 3D T1 measurements, can be addressed by Bloch equation analysis and experimental calibration. All three methods are validated in phantom studies, and the ‘Dual-τ Dual-FA’ and ‘Four-FA’ methods are validated in human brain studies using standard partial saturation and spin-echo methods for reference. The new methods offer a minimum-acquisition option for imaging single-component T1, T2, and PD. Four-FA’ performs best overall in accuracy, with high efficiency per unit accuracy versus existing methods when B1-inhomogeneity is appropriately addressed.
Keywords: MRI, spin-spin relaxation, spin-latice relaxation, proton density, measurement, B1 Correction
1. INTRODUCTION
The hydrogen (1H) spin-spin (T2), and spin-lattice (T1) relaxation times of water and proton density (PD) in healthy, diseased and treated biological tissue, are fundamentally responsible for image contrast and the success of magnetic resonance imaging (MRI) in medicine and biology. Nevertheless, the explicit imaging of T1, T2, and PD is rarely performed in clinical MRI exams, due to confounding factors affecting accuracy and to scan-time limitations. Indeed, the imaging of T1, T2, and PD is routinely supplanted by proxies such as T1- and T2-weighted image intensities. As a result, MRI scanner settings, being empirically derived, may not be optimized for contrast and detecting a particular disorder. Moreover, image intensities recorded at different MRI centers are generally not quantitatively comparable, and much potentially diagnostic T1 and T2 information, is simply not collected.
This is not to say that no efficient MRI relaxometry methods for jointly imaging T1, T2 and PD are available. Six such methods are compared in Table 1. Of these, those employing steady-state free-precession (SSFP) sequences (eg, “DESPOT1” and “DESPOT2”[1], “TrueFISP” T1 and T2[2], and “TESS”[3]) are acutely sensitive to non-uniformity in both the main magnetic field (B0) and in the transverse RF excitation field (B1). Such non-uniformities tend to increase with B0. Although the short SSFP sequence repetition periods (TR) save time, the effect of B1 errors in the excitation flip-angle (FA) accumulates faster than in long-TR sequences, necessitating careful B1 calibration. Short-TR SSFP is also prone to magnetization transfer (MT) errors[4]. The “FARM” method[5] (based on the “Look-locker” approach[6]), the inversion-recovery (IR) TrueFISP[2], and the IR-snapshot FLASH[7] methods sample the transient T1 recovery curve, with acquisition strategies that can be optimized to minimize scan-time[8]. The latest “MR fingerprinting” (MRF) technique[9] also provides T1, T2, and PD imaging capabilities based on a look-up table of solutions to the Bloch equations obtained by numerical simulation. Accommodations in the modeling for the effects of non-uniform B1, off-resonance, and T2* in the absence of spin-echoes, are anticipated to be important for the accuracy of those results as well. For all approaches, the central requirements are that T1- and T2-dependence be imposed on the MRI signal; that this dependence be varied in repeat applications of the MRI pulse sequence; and that the resultant T1, T2 and/or PD-dependence can be separately deciphered from the resultant signals, thereby enabling the corresponding parametric images to be reconstructed.
Table 1.
Summary of common methods for measuring T1, T2, and M0. The techniques presented in this work are shaded in grey.
| Measured parameters |
SteadyState(SS) or Transient |
# of Acqs |
TR | SSFP or SPGR |
comments | |
|---|---|---|---|---|---|---|
| DESPOT1[1] | T1 only | SS | 2 | short(6ms) | SPGR | Requires B1 mapping. |
| DESPOT2[1] | T2 only | SS | 2 | short(4ms) | SSFP | Requires B1 mapping and prior T1 knowledge. |
| IR TrueFISP[2] | T1, T2, PD | Transient | >38 | short(<6ms) | SSFP | Assumes uniform B1, B0. |
| FARM[5] | T1 only | Transient | 2 | short(6ms) | SPGR | Sensitive to FA errors |
| TESS[3] | T1, T2 | SS | 3 | 21ms | SSFP | T1 sensitive to B1 errors |
| MRF[8] | T1, T2, M0 | Transient | 1000 | 10–15ms | SSFP | Requires knowledge of B1 and spiral readout. |
| Dual-τ Dual-FA | T1, T2 and PD | SS | 3 | 609ms | SPGR | Requires B1 mapping. Narrow T2 range |
| Dual-τ Dual TR | T1, T2 and PD | SS | 3 | 530/1060ms | SPGR | Requires B1 mapping. Wider T2 range than ‘Tri-τ’. |
| Four FA | T1, T2, PD and FA | SS | 4 | 600ms | SPGR | B1 self-correction. |
Recently, we reported that self-refocusing B1-independent rotation (BIR-4) adiabatic pulses[10, 11] are prone to intra-pulse T2 decay that depends on the pulse duration (τ), B1 amplitude, and sweep frequency (fmax)[12]. This results from the time spent by the magnetization in the transverse plane during excitation[13]. Importantly, the T2 decay is independent of the FA, which can be arbitrarily chosen for these pulses[10]. As a consequence, T2-dependent attenuation of MRI signals is achievable simply by adding a long 0° BIR-4 pre-pulse to the MRI pulse sequence, leaving the sequence’s other excitation properties substantially unaffected[14]. With this ‘dual-τ’ T2 MRI method[14], T2 maps were obtained without spin-echoes, from the ratio of two steady-state signals acquired with two different pulse lengths but the same TRs. The present paper explores MRI methods that utilize this feature to image T2, T1, and PD in just three steady-state acquisitions, or four acquisitions if self-correction for inhomogeneity in the RF excitation field (B1) is included. This is the minimum number of acquisitions possible.
The T1 information can be encoded into a ‘dual-τ’ T2 MRI experiment by varying either the excitation FA[15, 16] or the TR [17] of the pulse sequence. This yields PD as well, but normally requires at least two more acquisitions, for a total of four. To image all three parameters-T1, T2, and PD–in three acquisitions, requires that both τ and either of TR or FA each be varied in at least two of the three acquisitions. Of these two options, we first evaluate the ‘Dual-τ Dual-FA’ method wherein TR is kept constant and a gradient-echo (GRE) MRI sequence is applied once with a small FA pulse, and twice more with the same large FA pulse, but preceded by either a short or a long 0° adiabatic pre-pulse. Next, the ‘Dual-τ Dual-TR’ experiment with a constant FA is evaluated. Here, a first MRI sequence is applied with a short adiabatic pre-pulse and a short TR; a second sequence is applied with a short 0° adiabatic pre-pulse and a long TR; and a third sequence uses both a long 0° adiabatic pre-pulse, and a long TR.
As with conventional methods for measuring T1, precise knowledge of the local FA is essential for accuracy. This means that both the ‘Dual-τ Dual-FA’ and ‘Dual-τ Dual-TR’ methods would effectively require at least two additional MRI acquisitions to map B1. While the standard B1 mapping software on clinical scanners is well-suited to providing FA information for three-dimensional (3D) MRI, correction for trans-slice B1 (FA) variations in 2D MRI requires repeat acquisitions to individually calibrate each sequence when the errors are T1-, TR-, and FA-dependent[18]. In the final method evaluated here, the spatial FA variation is recognized as integral to a complete T1, T2, and PD MRI experiment. We add just one acquisition to the ‘Dual-τ Dual-FA’ method to create the ‘Four-FA’ experiment which yields T1, T2, PD and FA (or B1) in just 4 acquisitions. The FA and T1 information is extracted from GRE signals acquired with three different FAs plus a short 0° adiabatic pre-pulse, while a long 0° adiabatic pre-pulse in the fourth acquisition yields T2. All three methods are validated in vitro, and the ‘Dual-τ Dual-FA’ and ‘Four-FA’ experiments are also demonstrated in human brain studies in vivo at 3 Tesla (T).
In what follows, we first describe how T2 is encoded for all three methods using long adiabatic pulses. To avoid confusion, each method is then presented serially with its own theory, experiment, and results section. Finally, the efficiency, accuracy, and efficiency per unit accuracy are compared in Monte Carlo simulations of the ‘Four-FA’ method with a combined partial saturation (PS) plus spin-echo (SE) experiment, and with the DESPOT1/2[1], IR TrueFISP[2], and MRF methods.
2. ENCODING T2
At time t = 0+ after a long FA=θ° adiabatic pulse of duration τ, the longitudinal magnetization, Mz, has magnitude:
| (1) |
compared to the start of the pulse at time 0−, where Ep is independent of FA (Ep=Epxy=Epz in Ref [14]). As described previously, the transverse magnetization is [12]:
| (2) |
with
| (3) |
where g is a parameter reflecting the time the magnetization spends in the transverse plane (eg, g =0.81 for 5 ≤τ ≤40ms, with fmax=15kHz, B1 =20µT; g =0.72 at fmax =5kHz, B1 =13.5µT)[14]. Note that off resonance effects within ±300 Hz do not alter the threshold for adiabaticity of the BIR-4 pulse, nor the attenuation factor, Ep, above the threshold.
Repeat application of the sequence at TR produces a T2-dependent steady-state signal:
| (4) |
assuming no net Mxy at the start of each sequence and E1=exp(-TR/T1) [14]. To perform T2 MRI, two steady-state signals are acquired: one with a long, and one with a short θ=0° adiabatic pre-pulse, both followed by a short GRE sequence[14]. While the short 0° adiabatic pre-pulse is in principle not needed, its inclusion can control for any effects arising in the period between the adiabatic pre-pulse and the GRE sequence. This principle is used for encoding T2 in all the methods below.
3. ‘Dual-τ Dual-FA’ MRI
3.1. Theory
In the ‘Dual-τ Dual-FA’ method, a single steady-state acquisition is added to the dual-τ T2 experiment to encode T1. Then, with both T1 and T2 in hand, the equilibrium magnetization, M0, is determined from the signal intensity to provide the PD image. The three acquisitions use the same TR, but are applied with two different excitation FAs, α and β. This part of the experiment is analogous to the dual-angle T1 method[16] where a=15° and β=60° were found to yield both useful T1-sensitivity and signal-to-noise ratio (SNR).
The ‘Dual-τ Dual-FA’ acquisitions specifically comprise: (A1) a first signal S1 excited by a conventional GRE MRI sequence with a short-α RF excitation pulse. In step (A2), a second signal S2, is excited by a 0° adiabatic pulse of duration τ2, followed by a GRE sequence with a β >α excitation pulse. A third signal S3, is excited in step (A3) by a 0° adiabatic pulse of duration τ3=2τ2 followed by a GRE sequence, also with FA=β. As noted above, adding a short (eg, 1ms) 0° adiabatic pre-pulse to A1, is prudent to control for the effects of the delay between the pre-pulse and signal acquisition in steps A2 and A3.
The derivation of E1 and Ep2=Ep(τ2) from S1, S2 and S3 is the same as presented earlier for NMR (as distinct from MRI) applications[14]. The solutions are:
| (5) |
with a = S1 sin β cos β sin β(S3–S2), b = S1S2 sin α cos α sin β–S2S3 sin2 α cos β and c = S2S3 sin2 α cos β – S1S3 sin α cos α sin β
| (6a) |
| (6b) |
| (6c) |
| (6d) |
, and
| (6e) |
for each image pixel. In practice, M0 (or PD) is calculated by extrapolating the magnetization in Eq. (6e) back to time zero based on the echo-time (TE) of the acquisition sequence, assuming mono-exponential T2 relaxation based on the T2 measurement from Eq. (6c).
3.2 Numerical simulations
Monte Carlo simulations of the nuclear magnetization were performed to determine the sensitivity of the relaxation measurements to noise. The simulations were performed by numerical analysis of the Bloch equations using Matlab software (Mathworks, Natick, MA)[19] with the standard deviation (SD) of the noise set at 2% of the signal strength for each sequence. The mean and SD (σT1) of the solution for T1 was determined from 100 runs for 0.3≤T1≤1.5s with T2=80ms as a function of TR, setting α=15° and β=60° as in the dual-angle method[16]. The mean and σT2 for T2 was determined with T1=1s for 0≤T2≤80ms. The adiabatic BIR-4 pulse length was set to τ3=2τ2=20ms, with B1=13.5µT, and fmax=5kHz to be consistent with the use of a Philips 3T MRI scanner’s body coil for excitation during validation experiments.
3.3. Experimental validation
A four-compartment phantom comprised of tubes with T1 and T2 values spanning that of brain matter (640 ≤T1 ≤1285ms and 35 ≤T2 ≤191ms) was prepared for in vitro validation studies, using agarose and CuSO4 solutions[20]. Their relaxation values were determined by standard PS and SE methods as detailed below. In vivo validation was performed in brain studies of healthy volunteers approved by the Johns Hopkins Institutional Review Board (IRB). Subjects were positioned supine and T1 and T2 measured by standard 3D PS and SE methods for comparison with ‘Dual-τ Dual-FA’ measurements.
All MRI was done on a Philips 3T Achieva MRI scanner (Philips Healthcare, Cleveland OH). The BIR-4 pulse FA was calibrated by ensuring a minimum signal at FA=0° for the pulse-lengths used[21]. The ‘Dual-τ Dual-FA’ method was validated using a Philips 8-channel SENSE receive-only head coil, with body coil excitation, and BIR-4 pulse parameters as simulated in Sec. 3.2. Under these conditions, the scanner’s RF power constraints limited TR to ≥609ms for acquisitions employing 20ms BIR-4 pulses.
Standard 3D PS T1 and SE T2 values were measured in every validation experiment to avoid any confounding temporal variations in T1 and T2. The same MRI spatial resolution, field-of-view (FOV), and bandwidth (BW) were used for each T1, T2, PD, and B1 mapping method being compared. The PS method employed a slab-selective 3D GRE sequence with TR=100, 300, 600, 900, 1200, 2000ms in vitro with FA=90°. The 3D SE method used 32 spin-echoes with TR/TE=1200/10ms. PS T1 and SE T2 values were calculated on a pixel-by-pixel basis using a nonlinear least-squares fit of the signal to the relaxation curves [w.exp(-TE/T2)+z] and [u-v.exp(-TR/T1)], respectively, with u,v,w and z as constants. The 3D B1 distribution determined by the AFI method (TR1/TR2=30/130ms, FA=45°), was taken as a standard for FA corrections. Because slice-profile errors are not accounted for in 3D AFI mapping, only the middle slices of slab-selective SE and PS MRI acquisitions were used for validation studies.
Coil receiver sensitivity maps were also computed based on the signal intensities of GRE images acquired from agarose phantoms (TR/TE=2 or 3s/3ms), and corrected for FA, T1 and T2. These were fitted to a 2D quadratic polynomial and used to normalize the calculated PD images, for the purpose of generating PD images in percent units (pu) relative to water[22]. The standard PD images were corrected for the FA, T1 and T2 using the applicable TR/TE values, as applied to the longest TR PS sequence. The ‘Dual-τ Dual-FA’ PD images were corrected with the ‘Dual-τ Dual-FA’ FA, T1 and T2values.
Phantom ‘Dual-τ Dual-FA’ T1 and T2 values were compared with PS and SE measurements as percentage differences from the standard values. The means ±SD were determined for each phantom compartment, and for brain regions-of-interest. In phantom ‘Dual-τ Dual-FA’ MRI experiments, S1 was acquired with a 15° GRE selective excitation, and S2 and S3 were excited by 0° BIR-4 pulses followed by 60° slab-selective 3D GRE sequences, with τ3=2τ2=20ms (TR/TE=609/3.5ms; total scan time=10.1min; elliptical k-space sampling, PE=330 phase encodes; 80×80×14 reconstruction matrix; FOV= 70×130×130mm; BW=117kHz; resolution=5×2×2mm; the central 7th coronal slice was analyzed). The FOV and matrix parameters were modified for human studies (FOV= 200×35×200mm, BW=180kHz; elliptically sampled k-space; PE=619; 224×224×7 reconstruction matrix; resolution=1×5×1mm; total scan time=18.9min, 4th axial slice analyzed).
3.4. Results
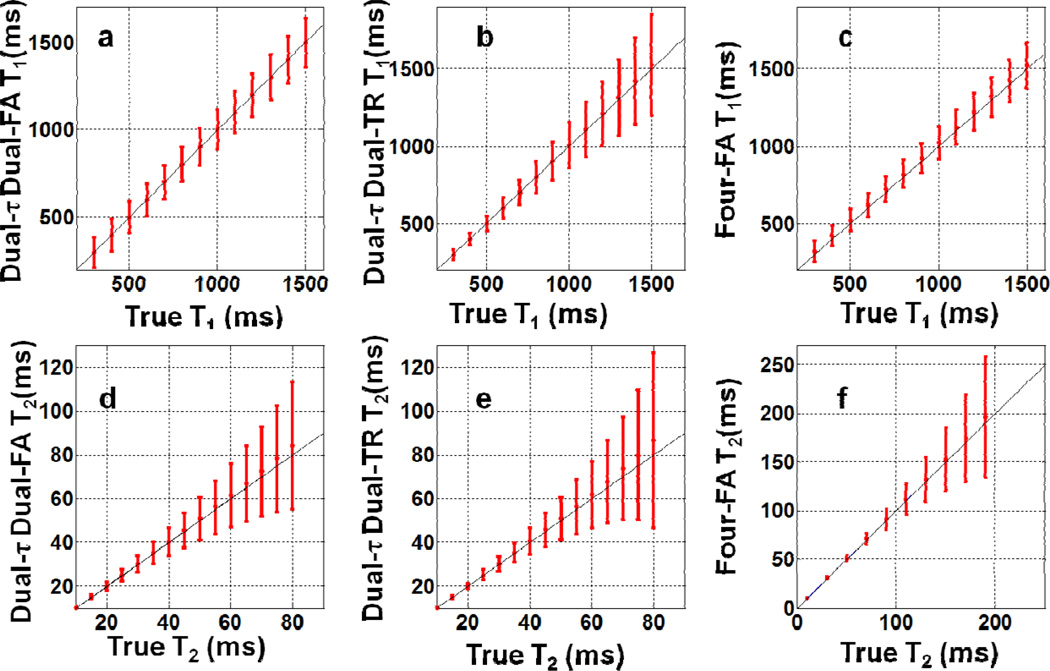
The Monte Carlo simulations show that T1 was unaffected by the pre-pulse length τ2. However, increasing TR above T1 did introduce a small (systematic) error in the mean T1 compared to the true value. With the shortest (scanner-limited) TR of 609ms and T2=80ms, the mean systematic error (±SD) in T1 was 0.6%±11% for T1=1 s (Fig. 1a). As a percentage, the SD in T1 decreased monotonically from 30% to 9% as T1 increased from 0.3s to 1.5s. With TR=609ms, τ2=10ms and T1=1s, the mean error for T2=45ms is 1%±18% (Fig. 1d).
Fig. 1.
(a–c) Monte Carlo simulations of the SD in T1(with T2 =80ms), and (d–f) T2 (with T1 =1s) with an SNR of 50, and 100 runs. Part (a) and (d) show results for the ‘Dual-τ Dual-FA’ method with TR=0.609s, τ3=2τ2 =20ms, and B1 =13.5uT. Part (b) and (e) show results for the ‘Dual-τ Dual-TR’ method with TR2 =2TR1 =1.06s, τ2 =2τ1=20ms, B1 =20uT. Part (c) and (f) are for the ‘Four-FA’ method with TR=0.6s, TR4 =1.032s, τ=20ms, B1 =20uT over a larger T2 range.
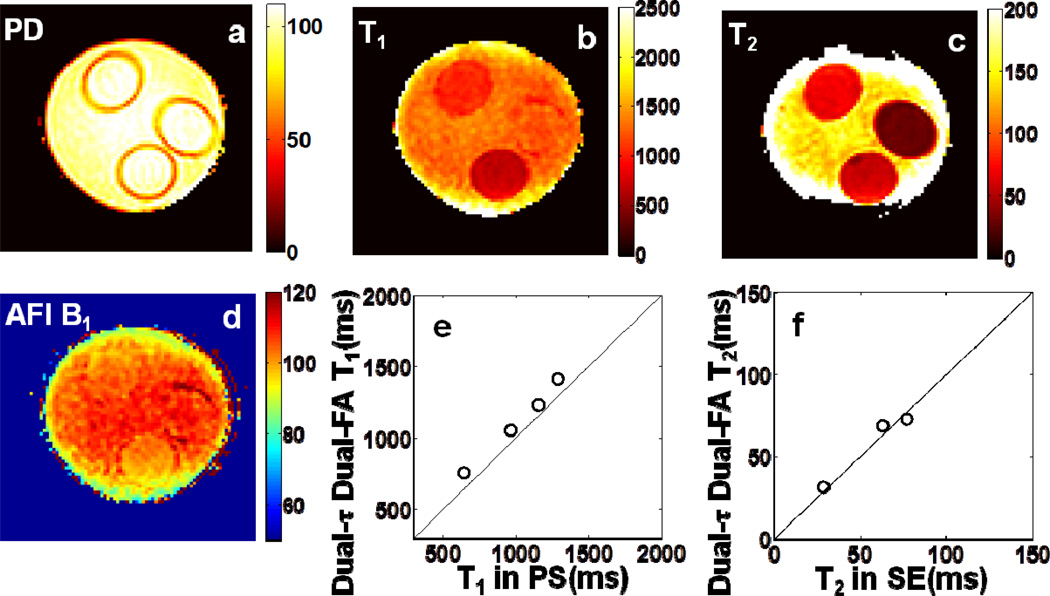
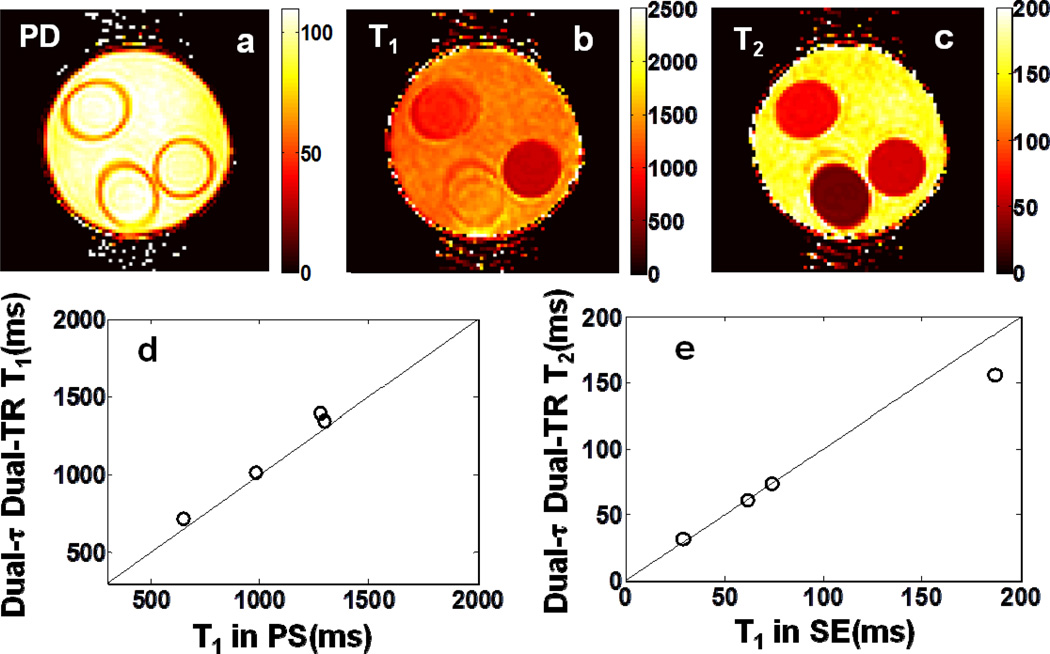
Experimental ‘Dual-τ Dual-FA’ T1, T2, and PD images of the phantom are shown in Fig. 2. The images were segmented into compartments using a region-growth algorithm. Aside from regions with T2>150ms which are not accurately determined by the ‘Dual-τ Dual-FA’ method[14], the errors in T2 were 3.9% ±6.5% vs SE (Fig. 2f). The error in T1 for the four segmented regions was 11% ±6.5% vs PS (Fig. 2e). The PD measured in pu[22], has an SD of 9.5% in the phantom (Fig. 2a).
Fig 2.
Color-coded ‘Dual-τ Dual-FA’ images of (a) PD, (b) T1, and (c) T2 in the three-tube bottle gel phantom. Part (d) shows an AFI B1 map of the phantom. Part (e) plots the ‘Dual-τ Dual-FA’ T vs. the standard PS T1 for each compartment. Part (f) plots the ‘Dual-τ Dual-FA’ T2 vs. SE T2 in the compartments (above 150ms, the ‘Dual-τ Dual-FA’ T2 is not accurate[14]). The black lines denote identity. The scales of PD is in pu, T1 and T2 maps are in ms, and the B1 map is % of the nominal FA.
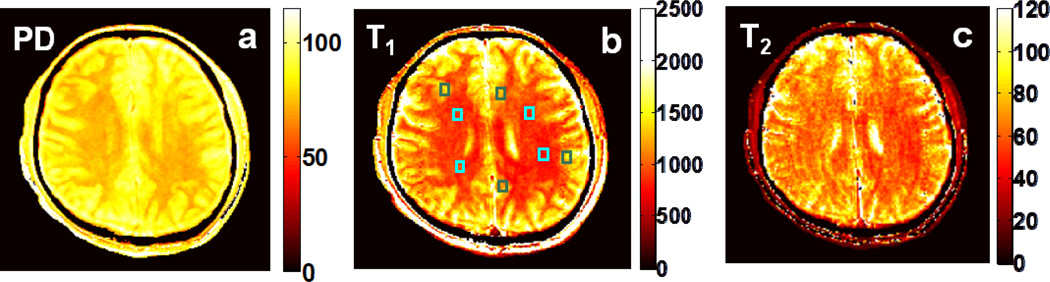
Fig. 3 depicts ‘Dual-τ Dual-FA’ brain MRI results. The ‘Dual-τ Dual-FA’ T1 values sampled in the annotated regions were 1.65 ±0.12s for grey matter (GM) and 1.06 ±0.08s for white matter (WM). These are consistent with literature values of: 1.33±0.001s[23], 1.47±.05s[24], and 1.82±0.11[25] for GM; and 0.83±0.01s[23], 1.08±0.05s[25], 1.11±0.05s[24], and 1.11s[26] for WM. The ‘Dual-τ Dual-FA’ T2 values were 68±9ms for GM and 54±5ms for WM, compared to SE results of 73±5ms and 54±5ms, respectively. Published T2 values for comparison are: 71±10ms[27], 99±7ms[25], and 110±2ms[23] for GM; and 56±4ms[27], 69±3ms[25], 80±0.6ms[23] for WM.
Fig 3.
Color coded ‘Dual-τ Dual-FA’ (a) PD, (b) T1 (b) and (c) T2 images from a healthy human brain. T1 and T2 values in the annotated squares in GM (green) and WM (blue) are compared with known values in the text. The scales are in pu (PD) and ms (T1 and T2).
4. ‘Dual-τ Dual-TR’ MRI
4.1 Theory
Instead of varying FA to encode T1 as in the ‘Dual-τ Dual-FA’ method, the ‘Dual-τ Dual-TR’ method varies TR along with τ in the following three acquisitions. (B1) A first signal, S1, is acquired in the steady-state at a short TR=TR1 using a short 0° adiabatic pre-pulse of duration τ1, followed by a GRE MRI sequence with an FA of φ. (B2) A second signal, S2, is acquired with a longer TR2=2*TR1 and the same τ1 0° adiabatic pre-pulse followed by the φ pulse, GRE sequence. (B3) A third steady-state signal S3 is acquired also with TR=TR2, but using an adiabatic pre-pulse of duration τ2=2τ1, followed by the same φ pulse, GRE sequence.
The three resulting signals are:
| (7) |
where Ep1 =Ep(τ1) and E1’=exp(-TR2/T1). Because τ2 = 2τ1, TR2=2TR1, we have Ep2=Ep12 and E1’=E12. This equation set can be solved by the numerical iteration of:
| (8) |
after setting initial values for E1 and Ep1. When (p=90° the solutions are analytic:
| (9) |
In all our experiments the FA was set nominally to φ = 90°. However, the presence of B1 inhomogeneities generally requires that a FA (or B1) map must be acquired and the local FAs substituted into the iterative algorithm. Initial values for Ep1 and E1 are calculated from Eq. (9). We recorded final values after ten iterations of Eqs. (8), but convergence was usually achieved at 4 iterations. T1 and T2 values were calculated by substituting Ep1 for Ep2 and τ1 for τ2 in Eq.(6c), and TR1 for TR in Eq. (6d). The value of TR1 is selected based on Monte Carlo error analysis of the Bloch equation as described below.
4.2. Numerical simulations
Monte Carlo simulations of the ‘Dual-τ Dual-TR’ method used the same noise, T1 and T2 ranges as in Sec. 3.2, but with FA=90° for all three GRE acquisitions. Because validation experiments for this method used the Philips system’s birdcage transmit/receive head-coil with a higher B1, we set B1=20µT, fmax=15kHz, and τ2=2τ1=20ms for the BIR-4 pulse. To determine a suitable TR1, the error in T1 was calculated from simulations performed with T1=1s and T2=80ms for 0.3 ≤TR1 ≤1.8s.
4.3. Experimental validation
Experiments were performed with the Philips’ head-coil and BIR-4 pulse parameters as simulated (Sec. 4.2). The same 4-compartment phantom used in ‘Dual-τ Dual-FA’ experiments (Sec. 3.3) was imaged. S1 and S2 were acquired with a τ1=10ms 0° BIR-4 pre-pulse followed by a nominal-90° slab-selective excitation with TR=530ms and 1060ms, respectively (FOV=70×130×130 mm; resolution=5×2×2mm; BW=117kHz; elliptically sampled k-space, PE=388; 80 ×80×7 reconstruction matrix; total scan time=17.1min, central 4th coronal slice analyzed). For step B3, S3 was acquired with the same nominal-90° selective excitation, but TR was limited to 1060ms by scanner RF power constraints on the τ2=20ms 0° adiabatic pre-pulse. Measured ‘Dual-τ Dual-TR’ T1 and T2 values were compared to standard SE and PS values acquired with the same experimental parameters used in the ‘Dual-τ Dual-FA’ experiments. Standard and ‘Dual-τ Dual-TR’ PD images were computed as in Sec. 3.3, except that the ‘Dual-τ Dual-TR’ PD images were corrected using the ‘Dual-τ Dual-TR’ T1 and T2 values.
4.4. Results
The Monte Carlo simulations of the ‘Dual-τ Dual-TR’ method showed that the SD of the estimated T1 decreased from 27% to 10% as TR1 increased from 0.3s to 1.2s (Fig. 4a), and that the choice of TR1 had little effect on the T2 measurement. We chose TR1=0.53s as a compromise between scan-time, T1 accuracy, and our scanner’s RF power constraints for τ1=10ms. With these settings, the T1 error of the ‘Dual-τ Dual-TR’ experiment varied from 0.6%±11% to 2%±22% for 0.3≤T1≤1.5s with T2=80ms. The T2 error for tissue with (T1, T2)=(1s, 45ms) was 1.8±17% (Fig. 1b, e).
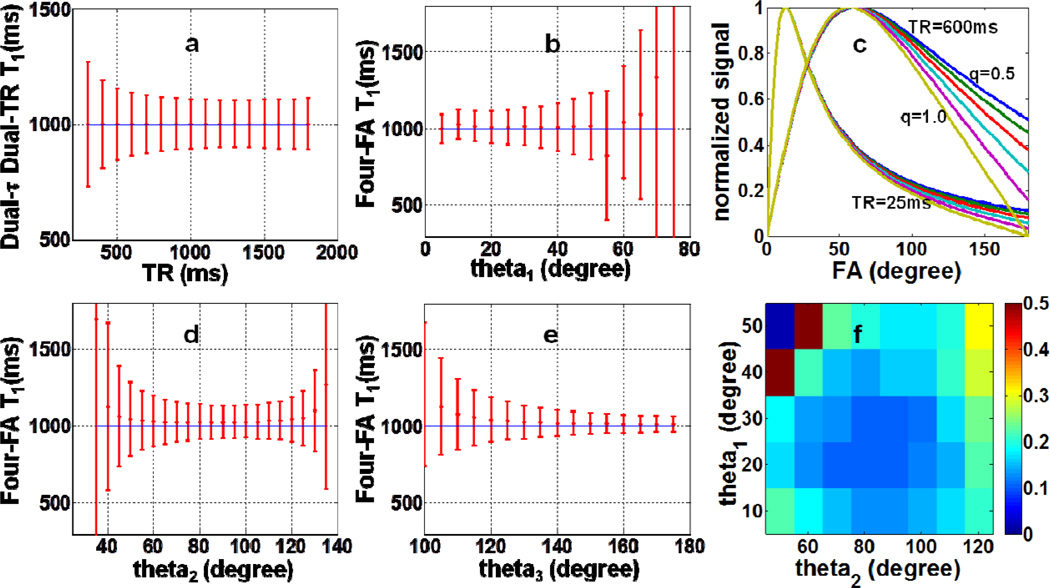
Fig 4.
Monte Carlo simulations used for selecting TR and FA: (a) the SD in the ‘Dual-τ Dual-TR T1 experiment as a function of TR; and the SD in the ‘Four-FA’ T1 experiment as a function of (b) θ1, (d), θ2, and (e) θ3, with each of the other two FAs set to the most favorable values (30°, 80°, 140°, respectively), and SNR=50. The horizontal blue line is the true (input) T1 value. Part (f) shows the SD in the ‘Four-FA’ T1 measurement as a function of θ1 and θ2, varied independently with a noise level=M0/100. The scale reflects the SD as a fraction of the true T1. (c) The normalized steady-state signal as a function of nominal FA for B1-field variations from 50–100% (q =0.5–1.0), TR=25ms and TR=600ms. B1 field differences can only be differentiated at long TR and high FA.
Experimental ‘Dual-τ Dual-TR’ T1, T2 and PD maps of the 4-compartment phantom are depicted in Fig. 5, with the relaxation values plotted below. The mean errors are 6.6±11% for T1 in the range 0.65≤T1≤1.3s; and 2.7%±5.2% for T2 in the range 29ms≤T2≤187ms. The SD of the PD signal is 8.8%.
Fig. 5.
In vitro color-coded Dual-τ Dual-TR (a) PD, (b) T1 and (c) T2 from the same phantom as Fig.2. Parts (d) and (e) plots the mean T1 and T2 values for the four compartments compared to measured standard PS and SE values (the black line is the identity line).
5. The ‘Four-FA’ MRI method
5.1 Theory
The accuracy of all of the above methods, including the standards, depends on accurate knowledge of the FA. Fast FA mapping techniques such as actual flip-angle imaging (AFI) or as provided by the MRI scanner manufacturer, require at least two acquisitions and are generally limited in accuracy to the central uniform region of selectively excited slices or slabs[28]. Thus, when FAs are uncertain and an FA map is required, even the minimum-acquisition ‘Dual-τ Dual-FA’ and ‘Dual-τ Dual-TR’ methods actually require at least five acquisitions to produce accurate T1, T2 and PD maps. This is greater than the minimum possible number of acquisitions–four, that could be used to measure the independent parameters T1, T2, PD, and FA. The ‘Four-FA’ method achieves this by incorporating an FA (or B1) determination in the same protocol.
The ‘Four-FA’ method acquires three steady-state signals S1, S2 and S3 from spoiled GRE MRI sequences each applied with the same TR=TR1, but different nominal FAs, θ1, θ2, and θ3 in steps C1-C3. A fourth signal, S4, is acquired in step C4, using a long 0° adiabatic pre-pulse of duration τ2 followed by a GRE sequence with FA=θ4, and TR=TR2. In these studies, we set the actual FAs equal to the nominal FAs scaled by a factor q that reflects the effect of a nonuniform B1-field at each (pixel) location. The four steady-state signals are thus:
| (10) |
Here, the B1 scaling factor, q, proton density M0, and T1 attenuation factor E1 are solved by three-coefficient least-squares fitting of the signal curve with x=[θ1, θ2, θ3], y=[S1, S2, S3], coeff=[M0, E1, q], minimizing ||F(x,coeff)-y||22 . T1 is obtained from E1. Then M0, q, and E1’ are substituted into the expression for S4 to obtain Ep2, from which T2 is obtained using Eq. (6a). Note that the value of T2 is determined by S4, after computing the other parameters from S1, S2, or S3 in Eq. (10). Also, by choosing θ4=θ1, the θ1 and M0 terms in S4 and S1 cancel in Eq. (10), enabling a direct computation of T2 from the ratio S4/S1, once T1 is known.
As noted earlier, short 0° adiabatic pre-pulses added to the three sequences in steps C1-C3 can control for the effects of the delay following the adiabatic pre-pulse used in step C4. The T2 attenuation from a 1ms pre-pulse, for example, is negligible (<3% for T2>13ms and <0.7% for brain tissue), and does not significantly affect the solution of Eq. (10) as presented. The values of θ1, θ2, and θ3 are chosen as those that minimize T1 quantification errors based on Monte Carlo simulations of the Bloch equations over an appropriate range of relaxation times. This results in at least one FA>90°.
5.2. Slice Profile Correction
The ‘Four-FA’ method can correct for an inhomogeneous B1 field, as long as the slice profiles excited by θ1, θ2 and θ3 have the same shape with magnitudes proportional to sin(q.θ). However, this does not hold for FA>90°[29] where signals from the edge of the profile can greatly exceed sin(q.θ) at the slice center (Fig. 6)[30]. For full or slab-selective 3D MRI[31], the middle slice of an excited slab is typically unperturbed by the slice profile, and yields accurate results even with short, truncated slab-selective excitation pulses. However, for 2D MRI employing a single slice selection with FA>90° pulses, the integrated effect of slice profile imperfections can be substantial. In this case, the T1 error can be calibrated by a factor generated by Bloch equation simulations and/or determined experimentally, as detailed below.
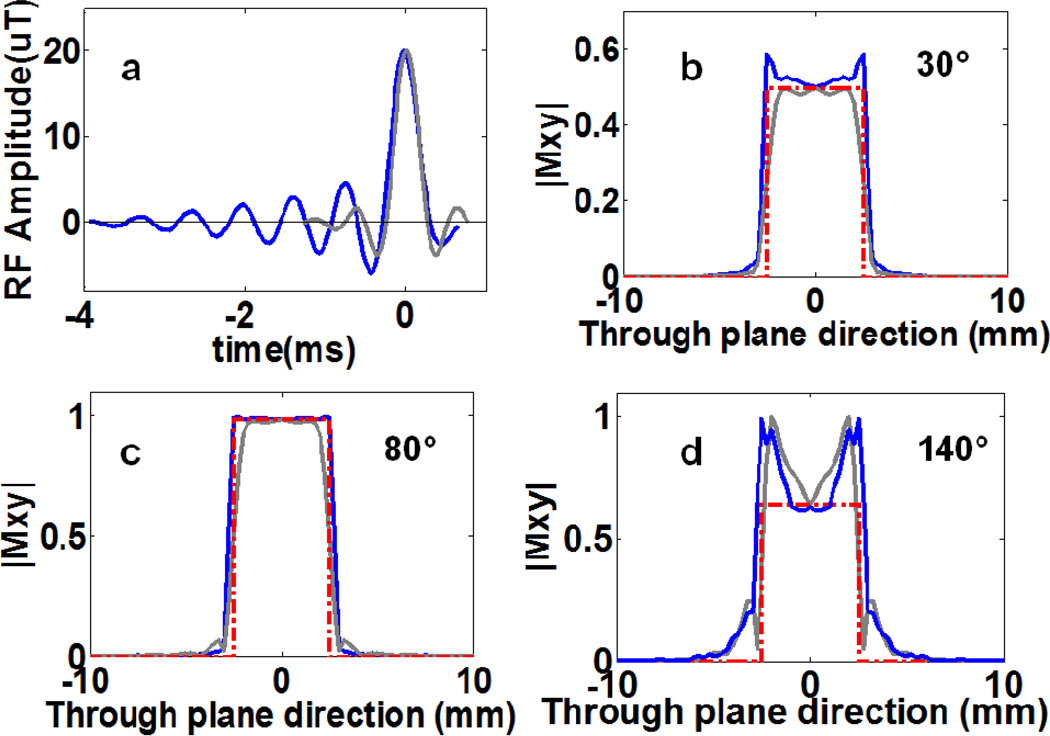
Fig. 6.
(a) Waveforms of ‘spredrex’ (blue) and truncated ‘sinc’(grey) FA=80° pulses used in our ‘Four-FA MRI sequences. The ‘spredrex’ pulse is more than twice as long as the truncated sinc pulse. Parts (b–d) show the slice profiles for the spredrex and sinc pulses determined from the magnitude of the transverse magnetization for (b) 30°, (c) 80°, and (d) 140° pulses used in the ‘Four-FA studies. The dashed red line is an ideal 5mm slice pulse profile.
5.3. Numerical simulations
Monte Carlo simulations of the ‘Four-FA’ method used the same T1 range as the earlier simulations, but a larger T2 range of 0≤T2≤190ms, and a noise level of M0/100 or an SNR of 50. The same BIR-4 pulse as the ‘Dual-τ Dual-TR’ was used with τ = 20ms[14]. FAs were successively incremented by 5° from 5°-180° to determine the values of θ1, θ2 and θ3 that minimized the error in T1. The rationale for setting the FAs is as follows. Fig. 4c shows that in order to differentiate B1, the signal curves should be sampled at FAs that span the range 0–180°, and that maximum differentiation occurring at the highest FA. If we allow a 25% variation in B1, the nominal FA cannot be greater than 140° lest the actual FA exceed 180°, which would cause aliasing. This sets the maximum FA for optimally differentiating B1 inhomogeneity at ~140°. The other two FAs are basically chosen to minimize the error in T1, based on the Monte Carlo simulations.
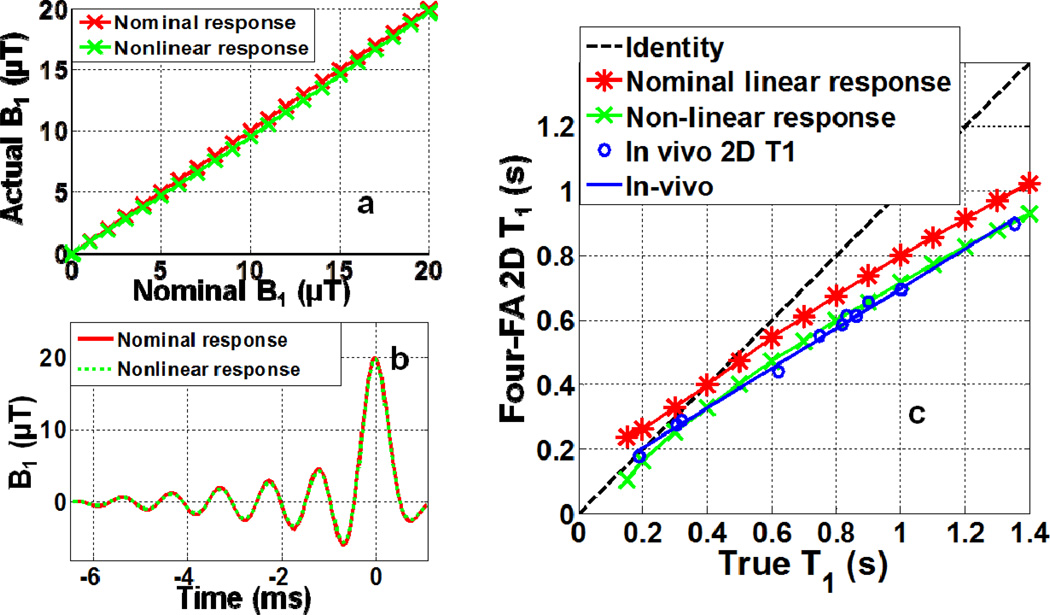
The effect of an imperfect slice profile is to alter the (q.θ) terms in Eq. (10) as a function of position across the slice (Fig. 6). This is not accounted by the global solution of Eq. (10). In addition to a standard ‘sinc’ pulse excitation, the Philips’ scanner can provide ‘spredrex’ excitation pulses (Fig.6a), which have an improved slice profile at high FA across the center of the slice, as compared to a truncated ‘sinc’ pulse (Fig.6d) [30]. A Bloch equation simulation of the effect of slice profile imperfections on T1 was performed by digitizing ‘spredrex’ pulses into 996 rectangular segments, with the pulse length, amplitude, and gradient strength set according to the scanner’s pulse viewer tool and T2=50ms and 100ms. The simulated ‘Four-FA’ T1 was compared with the true (input) T1, and a linear correction curve computed. To account for possible system non-linearity in the scanner’s delivery of the RF waveform to the coil, the response assuming a small quadratic term included in the output response, was also computed.
5.4 Experimental validation
The ‘Four-FA’ method was validated with a phantom comprised of 11 isolated gel-filled tubes spanning a broader range of T1 and T2 than used for the earlier methods (186 ≤T1 ≤ 1332ms, 13.2 <T2<227ms), and in IRB-approved studies of the human brain. A 1ms 0° adiabatic pre-pulse was added 9ms prior to slice-selective excitation in steps C1-C3, while step C4 used a 20ms BIR-4 pulse applied with the same pre-pulse delay. In phantom studies, S1-S4 were acquired using standard 2D and (slab-selective) 3D GRE MRI (TR1=600; TR2=1036ms; TE=1.9–3.0ms. 3D: FOV=25×160×160mm; resolution 5×2×2mm; BW=144kHz; elliptically sampled k-space; PE=353; reconstruction matrix 80×80×5; total scan time=16.7min, 3rd coronal slice analyzed. 2D: FOV=200×5×200mm; resolution=1×5×1mm; BW=180kHz; PE=200; reconstruction matrix 224×224; total scan time=9.6min) with nominal FAs of 01=30°, θ2=80°, 03=140°, and θ4=30°. Human brain studies utilized the same sequences, except that the 3D array had same-sized sections as 2D (3D FOV=200× 25×200mm; elliptically sampled k-space; PE=550; reconstruction matrix 224×224×5; resolution 1×5×1mm; BW=180kHz; total 3D scan time=26min, 3rd axial slice analyzed). The in vitro ‘Four-FA’ relaxation measurements were compared to 3D SE T2 data acquired with 14 echoes (TR/TE=500/15ms), and PS T1 measurements acquired the same as in Sec. 3.3. The in vivo ‘Four-FA’ measurements were compared with PS T1 data acquired using a slab-selective 3D GRE sequence at TR=100, 600, 1200ms and FA=90°; and with standard 32-echo 3D SE T2 data acquired at TR=725ms. Standard and ‘Four-FA’ PD images were computed as in Sec. 3.3, except that the ‘Four-FA’ PD images were corrected using the ‘Four-FA’ T1, T2 and FA values.
The effect of non-uniform slice profiles on the observed T1 for the 2D (slice-selective) ‘Four-FA’ method with the ‘spredrex’ pulse was measured in the 11-tube phantom, and the results compared to the numerical simulations with and without a small quadratic RF system response. The experimental results relating 2D ‘Four-FA’ T1 to 3D PS T1 were fitted to a linear regression line and used to correct 2D T1 values for slice profile effects. The T2 images were then recalculated using the corrected T1 values on a pixel-by-pixel basis.
5.5 Results
5.5.1 Numerical simulations
Bloch equation simulations of the ‘Four-FA’ method in Fig. 4c show that increasing TR increases the dispersion in steady-state signals elicited by different FAs, and improves the accuracy of T1 and B1 measurements. The Monte Carlo simulations show that the error in T1 decreases monotonically with increasing θ3 up to 180° (Fig. 4e). Setting θ3 = 140° to accommodate a ~25% B1 variation, the error in T1 increases monotonically with θ1, and has a minimum for θ2~80°. A plot of the SD in T1 wherein θ1 and θ2 are varied independently, confirmed that noise is minimal with a θ1 of 20°-30° and a θ2 of 70°-100° (Fig. 4f). Accordingly, we chose θ1=30°and θ2=80°.
Monte Carlo simulations performed with θ4=θ1 (to cancel the θ1 and M0 terms in Eq. 10) show that the uncertainty or SD in T2 is <3% for 20°≤ 04≤40°, and does not vary by more than 2% for choices of TR2 in the range 0.3<TR2<1s. Therefore, we chose the shortest TR allowed by the scanner for step C4: TR2 =1.032s. With TR1=0.6s, and T2=80ms, the simulations show that the uncertainty in T1 measured by the ‘Four-FA’ experiment decreases from 4±19% to 1.6±7.5% as T1 increases from 0.3 to 1.5s (Fig. 1c). With T1=1s, TR2=1.032s, τ=20ms, the error in T2 is ≤ 0.4±27%, increasing with T2 ≤190ms (Fig. 1f).
Results from the slice profile simulations comparing the apparent T1 with the true T1 for the ‘spredrex’ excitation used in the slice-selective (2D) ‘Four-FA’ experiment are plotted in Fig. 7. The star symbols (red) assume a linear RF field response. The crosses (green) show the effect of assuming a mild quadratic nonlinearity in the delivered RF field (Fig. 7a), which barely attenuates the pulses’ side-lobes (Fig. 7b). The integrated effect of the slice profile excitation was to reduce the observed T1 compared to the true T1: by about 20% and 28% at T1=1s, for the linear and non-linear profiles, respectively (Fig. 7c). These results did not change appreciably with T2.
Fig 7.
Effect of slice profile on T1. (a) Actual B1, or B1A, for a linear system response (red stars), and with (green crosses) a small second-order (B1A =0.004B1I2+0.91B1I) RF system response, as a function of input B1, denoted B1I. (b) Effect of the linear and second-order responses on the ‘Spredrex’ excitation waveform for a maximum B1 =20µT (FA=140°). (c) Bloch equation simulation of the ‘Four-FA’ T1 acquired with the 2D ‘Spredrex’ excitation pulse from (b), compared to the true T1 assuming linear (red stars) and non-linear (green crosses) RF system responses. Blue circles show the experimental results from the 11-tube phantom fitted to a straight line (R2=0.995; T12D =0.62T12D+81.3;blue line) that were used for calibration. Here, the 3D PS T1, denoted T13D , measurements are plotted as the ‘True T1’.
5.5.2. Experiments
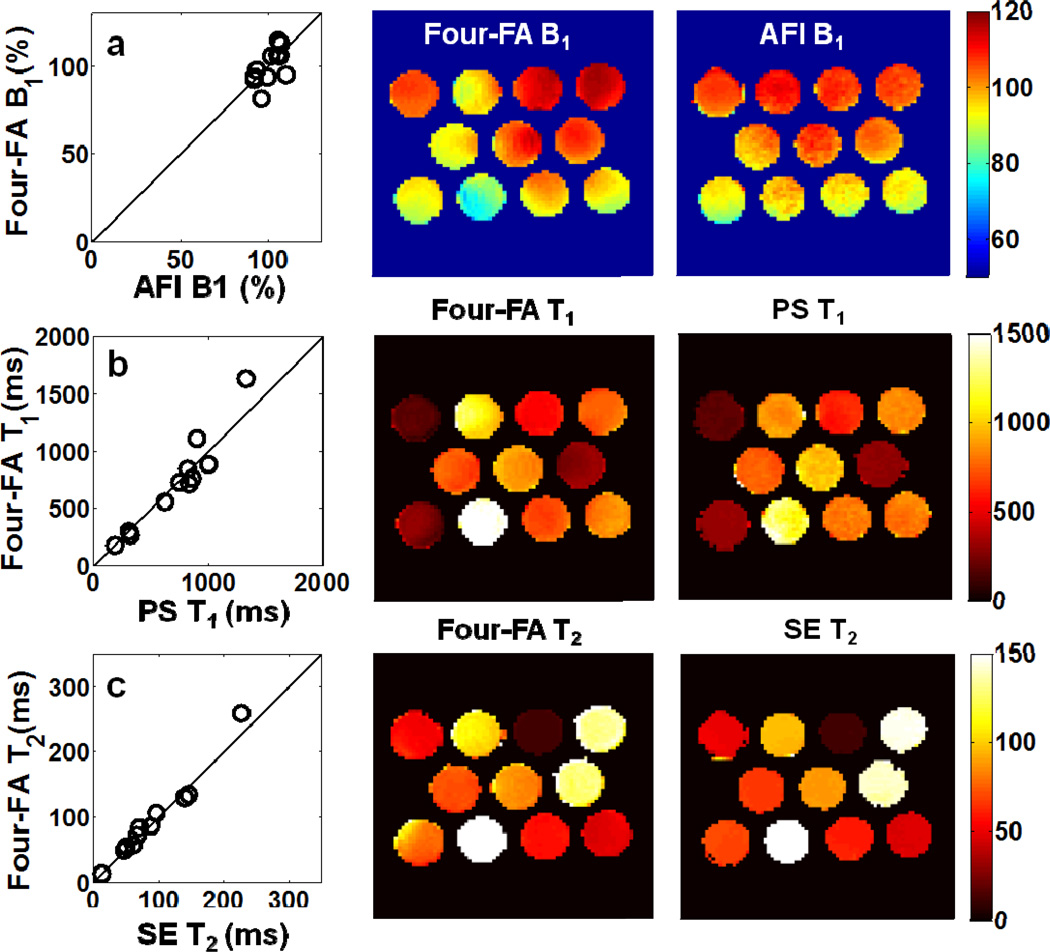
Fig. 8 compares 3D slab-selective ‘Four-FA’ T1, T2 and B1 maps with the standard images acquired from the 11-tube phantom. Mean ‘Four-FA’ values are plotted against standard values in the first column. Mean differences are all within 5%: the error in T1 is 2.5%±14% and the error in FA or B1 is 0.9%±8%. Even though the tube in the bottom left of Fig.8c has an anomalously poor B0 at its rim which compromises the performance of the adiabatic pulse used for the T2 determination, the error in T2 is just 3.6%±9%. The SD of the sensitivity- and T2-corrected PD image of the phantom was ±5.3% (not shown).
Fig. 8.
‘Four-FA’ results vs. reference values (column 1), and corresponding ‘Four-FA’ (column 2) and reference images (column 3) from the 11-tube phantom. Color scales are the same for each row (row a, B1 distribution, % nominal FA; row b, T1, ms; row c, T in ms).
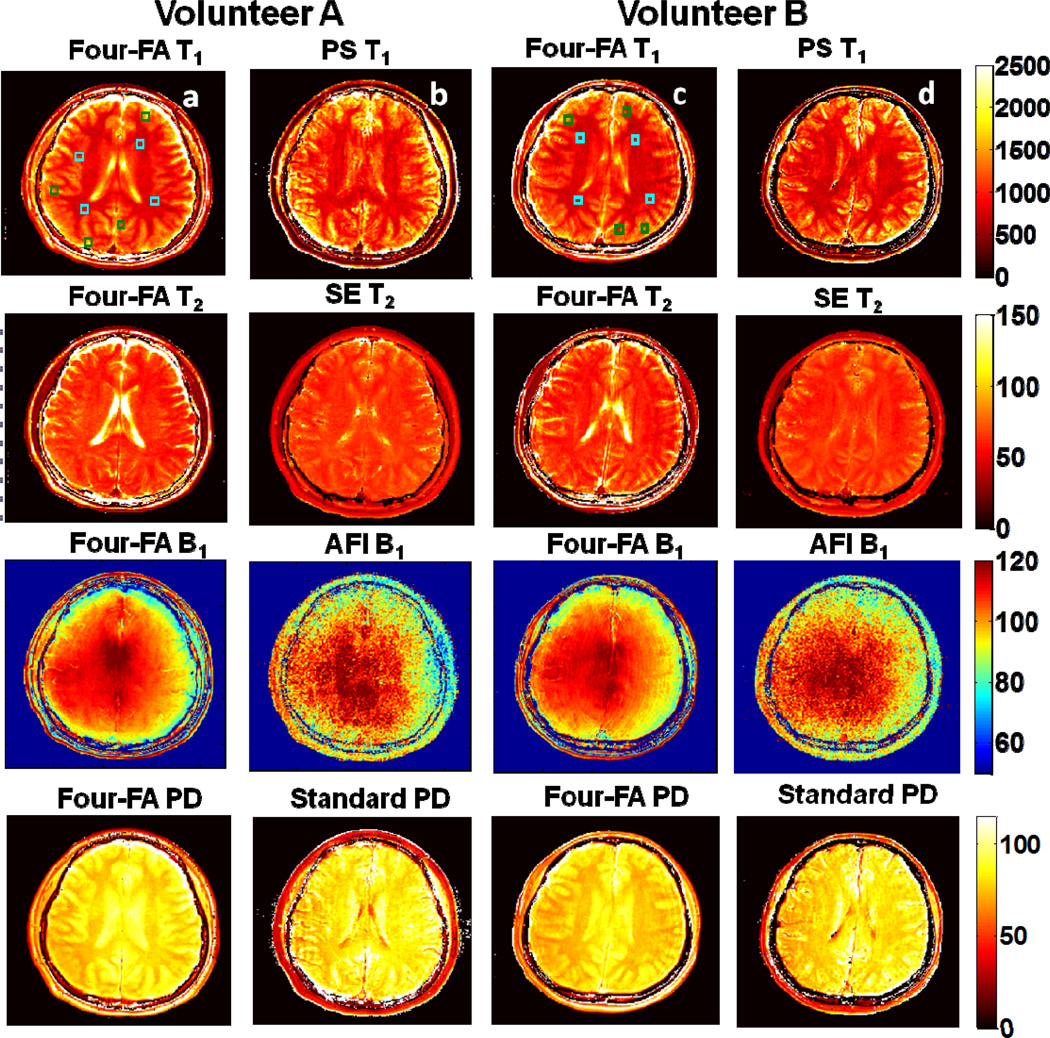
Fig. 9 shows 3D ‘Four-FA’ results from two volunteers. T1 and T2 values in the blue boxes in the WM region and the green boxes in the GM region are compared with standard T1 and T2 values from the same region. The mean ±SD error in T1 is −4.0±8.5% and −5.5±6.0% for volunteers A and B respectively. The T2 errors are 0.9±7.4% and 1.2±10.1%, respectively. For WM, the mean relaxation values are (T1, T2)=(859, 64.9) for volunteer A, and (865, 64.7) for volunteer B in ms. For GM, (T1, T2)=(1387, 75.4) and (1351, 77.0) in ms. These are consistent with prior published values listed in Sec. 3.4. On the other hand, contrast between cerebral spinal fluid (CSF) and neural tissue is poor in the standard PS T1 and SE T2 maps where the TRs (of 1.2s and 0.6s) are much less than T1 and T2 of CSF (in the range of 4/2s)[9]. Indeed, all of the T1 and T2 measurements of CSF appear lower than literature values, although the ‘Four-FA’ images provide much higher contrast between CSF and WM.
Fig. 9.
In vivo 3D ‘Four-FA images for two healthy volunteers (A, column a; B, column c) compared with corresponding standard maps from the same subjects (columns b and d, respectively). The maps are depicted with the same scales at right. The T1 and T2 scales are in ms, the B1 scale is in % and PD is in pu. ‘Four-FA’ relaxation values in the annotated boxes are compared with PS T1 and SE T2 values in the text. The poorer SNR and CSF contrast in the standard T1and T2 maps is attributable to the TR settings used for these studies.
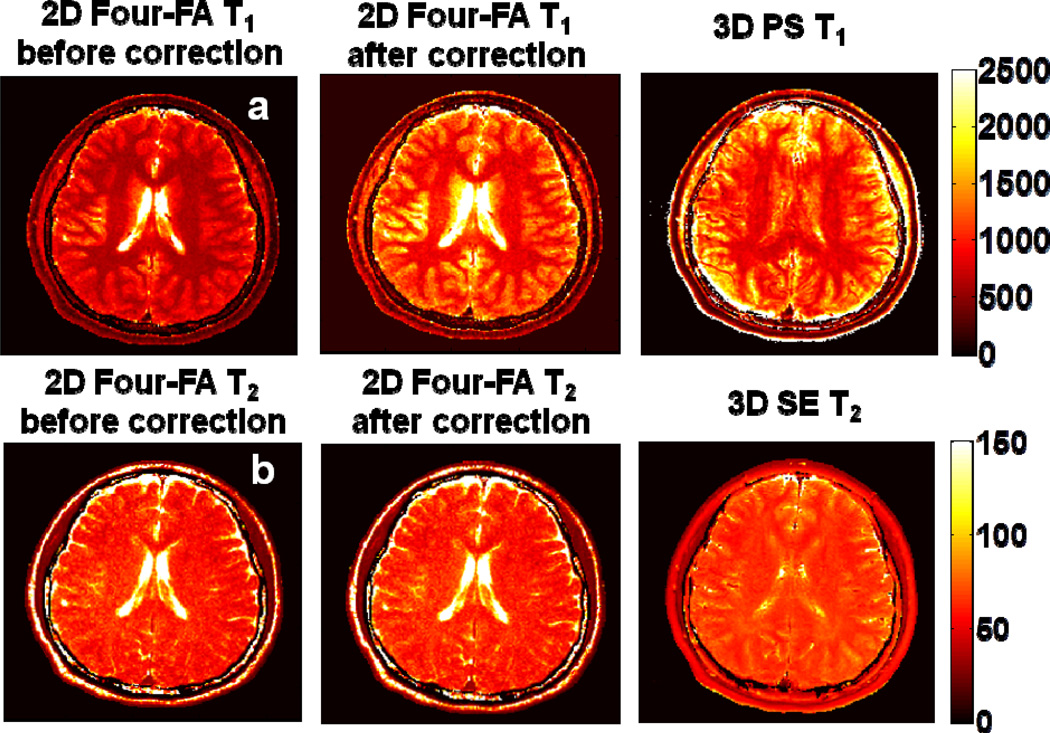
A comparison of the 2D slice-selective ‘Four-FA’ T1 measurements with the standard 3D PS T1 measurements taken as the ‘True T1’, is included in Fig. 7(c). The empirical data (blue points and line; R2 =0.995) are consistent with the simulation (green) that assumes a small (0.004 B12) quadratic RF response. Fig.10 compares 2D ‘Four-FA’ brain T1 and T2 maps computed without and with the empirical slice profile correction, with corresponding 3D PS T1 and 3D SE T2 results which are not subject to slice profile effects. As expected, the correction primarily affects T1, reducing the 2D ‘Four-FA’ errors in the boxes that were annotated in Fig. 9 from −33±5% to −3.6±6% for T1, and from −9.7±3.8% to −8.5±3.6% for T2.
Fig. 10.
2D ‘Four-FA’ T1 (Row a) and T2 (Row b) before and after application of slice profile corrections, as compared to standard PS and SE measurements from the central slice of 3D data sets, which do not have the slice profile problem. GM and WM show good agreement with the standards. The data are from Volunteer A in Fig. 9, and the scales are in ms.
6. EFFICIENCY AND ACCURACY
6.1 Theory
The theoretical efficiency of a T1 method, ΓT1, has been defined as T1 divided by the SD in T1, per square-root of the scan time, σT1, for a unit random noise with SD=σ0 in the underlying signal[1, 32, 33]. By extension, the efficiencies in determining the mean values of T1, T2, B1 and PD (or M0) are:
| (11) |
where the σ’s are SDs in the respective measurements, and Ts is the total scan time for acquiring T1, T2, B1 and M0 in the combined experiment. Note that while the Г’s reflect the scatter in the measured parameters, they do not show the accuracy of the determinations. We therefore compute the fractional accuracy or systematic error, defined as the difference between the mean determination from the simulations and the ‘true’ input values, divided by the true value. Because accuracy is arguably as important as efficiency, we divide Гby the accuracy, Г/(mean error), to create a figure-of-merit reflecting the efficiency per unit accuracy.
6.2 Methods
The efficiency and accuracy of the ‘Four-FA’ method were determined by Monte Carlo simulations for true values of (T1, T2) = (860, 65ms) and (1360, 75ms) to approximate WM and GM relaxation, respectively, as measured in PS, SE and ‘Four-FA’ experiments. Simulations were also performed with (T1, T2) = (1000, 70ms), which falls in the middle of this range. 104 runs were performed with four levels of noise (σ0=M0/50, M0/100, M0/150 and M0/200) added to the theoretical signal strengths. For comparison, the efficiency and accuracy were also simulated for the following common and efficient T1, T2, and PD imaging methods: (i) standard PS (TR=0.1, 0.6, and 1.2s) combined with a multi-SE sequence (TR=0.5s; 14 echoes); (ii) DESPOT1/2[1] (TR=3.4ms, NEX=5; DESPOT1 FA=3°, 12°; DESPOT2 FA=20°, 80°); (iii) and IR TrueFISP[2] (with TR=6.46ms, NEX=5, FA=45°, 5s delay ever 21 PE steps, 38 images acquired). The efficiencies were calculated from Eqs. (11) with the duration of a standard AFI quence (FA=45°, TR1/2=30/130ms) added to all methods lacking a B1-mapping feature, in order to provide an equivalent comparison to the ‘Four-FA’ method. Efficiencies were also computed without the AFI sequence for reference. The T1 and T2 efficiency of the MRF method without AFI were determined from results presented in Ref. [9] that show it to have ~2.1 and ~1.6 times the T1 and T2 efficiencies as DESPOT1 and DEPOT2, respectively, at T1/T2 values of 985/67ms. The efficiency of MRF with AFI, assumed a 200×200 AFI image matrix[9].
6.3 Results
With σ0=M0/100 and input (T1, T2)=(1000, 70ms), the Monte Carlo simulation of the ‘Four-FA’ method yielded a mean T1 of 1007±114(SD) ms, that is, a mean error of 7ms or 0.7%. The scan time for one phase-encoded acquisition was 3TR1+TR2=0.6×3+1.036=2.836 s. Thus, the T1 efficiency of the Four-FA method was 1000/(114√2.836)=5.2, and its efficiency/error was 5.2/0.7=7.4. The efficiency and mean error for all the methods being compared are listed in Table 2. Except for the MRF method for which information is presently incomplete, DESPOT1/2 is the most efficient for T1 T2 mapping when no B1 mapping is included, as was previously reported[1]. However, adding AFI to provide B1-calibration reduces the T1 and T2 efficiency of DESPOT1/2 as compared to ‘Four-FA’, while DESPOT1/2 was 6-times less accurate. The ‘Four-FA’ method was at least twice as efficient as AFI in B1 mapping, and more than 50 times more accurate. The ‘Four-FA’ method outperformed in efficiency per unit accuracy for jointly measuring T1, T2, B1 (or FA), and PD, with the exception that PD measured with IR True-FISP had zero mean error. The efficiency and mean errors varied with T1, T2 and σ0, and typically improved with decreasing noise, σ0<M0/100. Analysis of the ‘Dual-τ Dual-TR’ and ‘Dual-τ Dual-FA’ methods showed they were less efficient than the ‘Four-FA’ method.
Table 2.
T1, T2, B1 and M0 efficiency, mean error (%), and {efficiency/mean error} for ‘Four-FA’ and relative quantitative mapping methods at T1=1s, T2=70ms and noise level =M0/100. Numbers in the brackets indicates the efficiency without the B1 mapping sequence (AFI).
| Four FA |
Standard with(w/o) AFI |
DESPOT1/2 with(w/o) AFI |
IR TrueFISP with(w/o) AFI |
MRF* with(w/o) AFI |
|
|---|---|---|---|---|---|
| T1 efficiency | 5.2 | 3.6 (3.7) | 4.5 (8.2)a | 2.0 (2.1) | 8.4 (16) |
| mean error(%) | 0.7 | 2.3 | 9.3 | 17 | − |
| efficiency/error | 7.4 | 1.6 (1.6) | 0.5 (0.9) | 0.1 (0.1) | |
| T2 efficiency | 4.7 | 7.2 (7.4) | 4.3 (7.9)a | 2.7 (2.8) | 6.3 (12) |
| mean error(%) | 1.4 | 4.5 | 9.5b | 8.7 | − |
| efficiency/error | 3.4 | 1.6 (1.6) | 0.5 (0.8) | 0.3 (0.3) | |
| B1 efficiency | 23 | 2.8 | 9 | 2.8 | 9.5 |
| mean error(%) | 0.06 | 3.2 | 3.2 | 3.2 | 3.2 |
| efficiency/error | 383 | 0.9 | 2.8 | 0.9 | 3 |
| M0 efficiency | 11.8 | 8.0 (8.3) | 9 (17) | 53(55) | − |
| mean error(%) | 0.2 | 02c | 3.6 | 0.03 | − |
| efficiency/error | 59 | 40 (42)c | 2.5 (4.7) | 1800 (1800) |
Notes: The relative standings of the methods vary with T1 & T2 as follows.
DESPOT1/2 has (<10%) higher efficiency than ‘Four-FA’ at (T1, T2)= (860ms, 65ms).
The error in DESPOT1/2<TrueFISP error at (T1, T2)=(860ms, 65ms).
The error and efficiency/error in the standard method are respectively lower and higher than ‘Four-FA’ at (T1, T2)=(1360ms, 75ms).
Efficiency was estimated from Fig. 5 of Ref. [9] at T1=985ms and T2=67ms (% error estimates from the figure, and M0 efficiency data were unavailable).
7. DISCUSSION
This paper extends the application of the T2 filtering property of 0° adiabatic pre-pulses to combined T1, T2 and PD imaging methods, by introducing three new imaging protocols that employ the minimum number of steady-state acquisitions possible. While the ‘Dual-τ Dual-TR’ and ‘Four-FA’ methods were not previously described, we note that the ‘Dual-τ Dual-FA’ method, was previously introduced as the ‘Tri-τ’ method for T1 and T2 measurements, but not for MRI[14]. In fact, inaccuracies in both T1 and T2 due to what turned out to be B0, B1 and slice profile effects when attempting MRI with the ‘Tri-τ’ method are what inspired the present work.
For a combined T1 and T2 MRI experiment, the use of 0° adiabatic pre-pulses have advantages over spin-echoes in avoiding the confounding effects of saturation that arise when the excitation pulses are non-90° or non-uniform[18, 34]. T2 accuracy is enhanced by including a short 0° adiabatic pre-pulse in at least one sequence, as a control. While SSFP sequences also generate stimulated echoes and provide sensitivity to all three of T2, T1 and M0[35], the peak of the true T2 echo signal actually falls at the center of the next excitation pulse[36]. Moving the echo to the center of the acquisition window by means of MRI gradients–as is invariably done in MRI-renders the signal prone to the effects of T2*, motion during the MRI gradients, as well as the usual B1 inhomogeneity and off-resonance effects.
Indeed, all existing T1 methods are prone to errors in B1 when deployed with sequence TRs ≤T1 and large FAs. We chose incoherent steady-state sequences for T1 encoding, because unlike transient methods (Table 1) they are amenable to the repeat acquisitions required for spatial encoding, which can allow greater versatility in adjusting the number of averages or spatial encoding steps than approaches that sample the transient recovery of the magnetization. The primary determinant of accuracy was B1 inhomogeneity which is intrinsically worse at 3T compared to lower fields, owing to RF penetration effects. When incorporated into 3D or slab-selective sequences with FA corrections provided by our scanner’s B1 mapping sequence, all of the new methods agreed experimentally with the standard 3D SE and PS methods within 11%. However, in 2D slice-selective sequences, even though the ‘Four-FA’ method yielded results comparable to standard 2D slice-selective SE and PS measurements, the T1 measurements–including those acquired with standard 2D PS-all differed significantly from the 3D measures. This is attributable to the inadequacy of the scanner’s AFI method for addressing slice profile effects[28]. Even so, adding a 2D AFI correction to the 2D measurements did not fully correct for the T1 differences between any of the 2D images and the 3D PS results acquired for reference. This means that the FA measured by the scanner’s standard AFI protocol was insufficient to permit accurate correction of T1 measured by 2D MRI.
Since FA is so critical to accuracy, and B1-inhomogeneity is more problematic at ≥3T fields, it makes most sense to formally integrate the FA or B1 correction, into the whole T1, T2 and PD imaging method, as exemplified by the ‘Four-FA’ method. This also ensures that the correct FA information specific to the actual T1 or T2 sequence(s) is acquired, which is typically not the case when standard AFI sequences are run. Combining the FA meaurement with the addition of only one acquisition via the ‘Four-FA’ method, improves the overall efficiency as compared to adding the at-least-two acquisitions required for AFI, to an existing method.
In fact, when B1 corrections derived from the scanner’s AFI protocol were used, both in vivo and in vitro studies yielded ‘Dual-τ Dual-FA’ T1 maps that were systematically slightly higher than the PS T1 maps (Fig. 5). Because results from a conventional (non-MRI) ‘Dual-τ Dual-FA’ T1 NMR experiment previously demonstrated essential agreement with standard methods [14], we attributed the difference to the inadequacy of the scanner’s AFI B1 mapping protocol in replicating the FA distribution that was in effect during the ‘Dual-τ Dual-FA’ experiment. This was confirmed by phantom 2D ‘Four-FA’ validation experiments which revealed AFI B1 values that were ~12% lower than the ‘Four-FA’ B1, and by numerical simulations of the effects of such B1 errors on T1. Indeed, when the effective B1 was measured using fully-relaxed experiments in which the FA was varied and the NMR signal fit to a sine curve, the ‘Four-FA’ B1 was observed to agree with the measured B1 to within 0.4%. Clearly, greater accuracy in B1 mapping would at least improve the accuracy of ‘Dual-τ Dual-FA’ measurements, and likely T1 measured by other methods as well. In this regard, note that the SNR of ‘Four-FA’ B1 is more than twice that of the scanner’s AFI B1 map (Fig. 9).
Because the ‘Dual-τ Dual-TR’ method uses the same FA ~90°, it is relatively insensitive to B1 mapping errors. The in vitro validation indicated accurate T1 and T2 mapping over a wide range of T1 and T2. However the scanner’s built-in RF power constraints limited the shortest TR to ≥530ms for the Philips transmit/receive head coil, whereupon doubling the TR in steps B2 and B3 resulted in a total acquisition time that was comparable to a conventional T1 measurement. Consequently, we did not validate the ‘Dual-τ Dual-TR’ method in vivo. The RF power associated with long adiabatic pulses is a significant limitation on long-τ acquisitions due to regulatory compliance[12]. It does not help that scanner power limits can over-state the deposited power by 2.2-fold or so[37].
The ‘Four-FA’ method self-corrects for FA inhomogeneity. While it has been suggested that varying FA to estimate B1, M0 and T1 is an ill-posed problem[38], we have demonstrated that the three parameters can be fairly accurately estimated from a least possible number of acquisitions (Fig. 4c). Generally, TR should be chosen generally in a range ~T1/2, but the simulations and experiments show that a fixed TR of 600ms yields accurate results for TR/3≤T1≤ 2.5TR (Fig. 1c, Fig. 8b). With 03>90°, the slice profile of the S3 acquisition of the ‘Four-FA’ method develops serious horns (Fig. 6d) which requires an additional correction for 2D MRI applications (Fig. 7c). A similar correction for FLASH T1 imaging was previously reported[39], and other slice-selective T1 imaging methods are likely to require FA- and/or TR-dependent slice-profile corrections beyond those provided by conventional B1 or AFI mapping to achieve accurate results. The need for such correction would be signified by the presence of differences between T1s measured in 2D and 3D images of the same subject or phantom. This, along with the fact that the image resolution along the slice selection direction usually can’t match that achievable with 3D MRI, however, may be considered minor disadvantages of 2D T1 MRI compared to the speed-up realized by reducing the number of phase encodes vs. 3D.
Despite having the minimum theoretical number of steady-state acquisitions possible, the ‘Four-FA’ method nevertheless exhibited only average efficiency as defined by the conventional Г’ metrics, in Monte Carlo simulations (Table 2). Its efficiency was poorer than both multi-SE (with 14 echoes) and MRF. However, the overall accuracy of the ‘Four-FA’ method was much better than SSFP based measurements and SE, which is not accounted for in the Γmetrics. The efficiency per unit accuracy, Г/(mean error), of the ‘Four-FA’ method was generally many times higher than the other methods, with the caveat that we presently do not know whether the newest MRF approach[9] accommodates T2*, B1 and slice profile effects in its library of solutions.
The primary reason for the longer acquisition times for all of the new methods proposed here, and for the ‘Four-FA’ method’s lower Гs compared to SSFP-based measurements (DESPOT1/2, IR TrueFISP, MRF), is their longer TRs. Here at 3T, the TRs were limited by RF power constraints on the long adiabatic pulses. A simple fix to this problem could be switching to a lower field. At 1.5T, for example, the SAR would be reduced to 25% or more, depending on how the scanner treats the regulatory limits on peak power. In this case, the TR in ‘Dual-τ Dual-FA’ and ‘Dual-TR Dual-FA’ could be reduced four-fold, reducing the total scan time to less than 5 mins for 7 slices in Figs 2, 3, 5, for example. For the ‘Four-FA’ method, SAR only affects the final acquisition with the long BIR-4 pulse, which again would be reduced four-fold at 1.5T. The ‘Four-FA’ method is in addition affected by the need for a long TR to ensure accurate B1 measurements. As discussed, accurate knowledge of B1 is critical to the credibility of all T1 methods (PS, IR, DESPOT1, IR-TrueFISP). If B1 is known, reducing TR from 600ms down to ~10ms for the ‘Four-FA’ method for example, not only reduces the scan time, but also results in a 11–22% higher T1 efficiency (without the last acquisition) than DESPOT1 without AFI, while still maintaining its advantage of a much smaller mean error of <2%. Indeed, the much higher accuracy seen with the ‘Four-FA’ method (Table 2) is in good part due to the longer TR required for a much more accurate B1 determination.
Implicit in the development of any minimum-acquisition T1 and T2 MRI protocols is the assumption that the number of relaxation components is limited. Here we have assumed that both are mono-exponential. Indeed, single-valued T1s and T2s are commonly reported for human studies, and often represent the only data available from MRI studies at a given B0. This is not to say that multiple components do not exist. Also, multi-component relaxation may not be distinguishable from mono-component relaxation combined with tissue heterogeneity, for example, due to mixtures of GM, WM and CSF present in brain pixels. However, in our PS and SE experiments acquired at multiple time points during relaxation, we found no evidence of multi-exponential decays that could not as easily be characterized by a single exponential. Moreover, the ‘Four-FA’ method measures T1 and T2 intrinsically differently from the PS and SE methods–and at different time scales. If T1 or T2 relaxation were multi-component, agreement would have been be problematic.
In conclusion, the validation studies show results consistent with mapping using standard methods, and with prior published relaxation values for brain WM and GM tissue at 3T. The three methods described offer a minimum-acquisition option for imaging single-component T1, T2, and PD, potentially offering considerably higher efficiency per unit accuracy in the context of existing approaches, when B1-inhomogeneity and slice profile affects are appropriately addressed.
Highlights.
T1, T2, and proton density (PD) determine contrast in clinical MRI, but are not routinely imaged.
Three new methods for directly imaging T1, T2, and proton density (PD) are presented
All methods use the minimum possible number of steady-state acquisitions
The ‘Four-FA’ MRI includes self-correcting B1-mapping and slice profile correction.
‘Four-FA’ MRI exhibits excellent performance for accuracy and efficiency/accuracy.
Acknowledgement
We thank Dr. Shashank Hedge, Yi Zhang, of the Division of MR Research, and Ying Cheng of the Kirby fMRI center at Johns Hopkins University for helpful discussions and assistance with human studies. The work was supported by NIH grant R01 EB007829.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- 1.Deoni SCL, Rutt BK, Peters TM. Rapid combined T1 and T2 mapping using gradient recalled acquisition in the steady state. Magnetic Resonance in Medicine. 2003;49:515–526. doi: 10.1002/mrm.10407. [DOI] [PubMed] [Google Scholar]
- 2.Schmitt P, Griswold MA, Jakob PM, Kotas M, Gulani V, Flentje M, Haase A. Inversion recovery TrueFISP: Quantification of T1, T2, and spin density. Magnetic Resonance in Medicine. 2004;51:661–667. doi: 10.1002/mrm.20058. [DOI] [PubMed] [Google Scholar]
- 3.Heule R, Ganter C, Bieri O. Triple echo steady-state (TESS) relaxometry. Magnetic Resonance in Medicine. 2013 doi: 10.1002/mrm.24659. n/a-n/a. [DOI] [PubMed] [Google Scholar]
- 4.Bieri O, Scheffler K. On the origin of apparent low tissue signals in balanced SSFP. Magnetic Resonance in Medicine. 2006;56:1067–1074. doi: 10.1002/mrm.21056. [DOI] [PubMed] [Google Scholar]
- 5.Tong CY, Prato FS. A novel fast T1-mapping method. Journal of Magnetic Resonance Imaging. 1994;4:701–708. doi: 10.1002/jmri.1880040513. [DOI] [PubMed] [Google Scholar]
- 6.Look DC, Locker DR. Time Saving in Measurement of NMR and EPR Relaxation Times. Review of Scientific Instruments. 1970;41:250–251. [Google Scholar]
- 7.Haase A, Matthaei D, Bartkowski R, Dühmke E, Leibfritz D. Inversion recovery snapshot FLASH MR imaging. Journal of computer assisted tomography. 1989;13:1036. doi: 10.1097/00004728-198911000-00016. [DOI] [PubMed] [Google Scholar]
- 8.Ehses P, Seiberlich N, Ma D, Breuer FA, Jakob PM, Griswold MA, Gulani V. IR TrueFISP with a golden-ratio-based radial readout: Fast quantification of T1, T2, and proton density. Magnetic Resonance in Medicine. 2013;69:71–81. doi: 10.1002/mrm.24225. [DOI] [PubMed] [Google Scholar]
- 9.Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold MA. Magnetic resonance fingerprinting. Nature. 2013;495:187–192. doi: 10.1038/nature11971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Garwood M, Ke Y. Symmetric pulses to induce arbitrary flip angles with compensation for rf inhomogeneity and resonance offsets. Journal of Magnetic Resonance (1969) 1991;94:511–525. [Google Scholar]
- 11.Robin Bendall M, Garwood M, Uurbil K, Pegg DT. Adiabatic refocusing pulse which compensates for variable of power and off-resonance effects. Magnetic Resonance in Medicine. 1987;4:493–499. doi: 10.1002/mrm.1910040510. [DOI] [PubMed] [Google Scholar]
- 12.El-Sharkawy A-M, Schar M, Ouwerkerk R, Weiss RG, Bottomley PA. Quantitative Cardiac 31P Spectroscopy at 3 Tesla Using Adiabatic Paulses. Magnetic Resonance in Medicine. 2009;61 doi: 10.1002/mrm.21867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.De Graaf RA, Nicolay K. Adiabatic rf pulses: Applications to in vivo NMR. Concepts in Magnetic Resonance. 1997;9:247–268. [Google Scholar]
- 14.Wang G, El-Sharkawy AM, Edelstein WA, Schär M, Bottomley PA. Measuring T2 and T1, and imaging T2 without spin echoes. J. Magn. Reson. 2012;214:273–280. doi: 10.1016/j.jmr.2011.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fram EK, Herfkens RJ, Johnson GA, Glover GH, Karis JP, Shimakawa A, Perkins TG, Pelc NJ. Rapid calculation of T1 using variable flip angle gradient refocused imaging. Magnetic Resonance Imaging. 1987;5:201–208. doi: 10.1016/0730-725x(87)90021-x. [DOI] [PubMed] [Google Scholar]
- 16.Bottomley PA, Ouwerkerk R. The Dual-Angle Method for Fast, Sensitive T1 Measurement in Vivo with Low-Angle Adiabatic Pulses. Journal of Magnetic Resonance, Series B. 1994;104:159–167. [Google Scholar]
- 17.Freeman R, Hill H. Fourier transform study of NMR spin-lattice relaxation by “Progressive Saturation”. The Journal of Chemical Physics. 1971;54:3367. [Google Scholar]
- 18.Edelstein WA, Bottomley PA, Hart HR, Smith LS. Signal noise and contrast in nuclear magnetic resonance (NMR) imaging. J Comput Assist Tomogr. 1983;7:391–401. doi: 10.1097/00004728-198306000-00001. [DOI] [PubMed] [Google Scholar]
- 19.Bittoun J, Taquin J, Sauzade M. A computer algorithm for the simulation of any Nuclear Magnetic Resonance (NMR) imaging method. Magnetic Resonance Imaging. 1984;2:113–120. doi: 10.1016/0730-725x(84)90065-1. [DOI] [PubMed] [Google Scholar]
- 20.Yoshimura K, Kato H, Kuroda M, Yoshida A, Hanamoto K, Tanaka A, Tsunoda M, Kanazawa S, Shibuya K, Kawasaki S, Hiraki Y. Development of a tissue-equivalent MRI phantom using carrageenan gel. Magnetic Resonance in Medicine. 2003;50:1011–1017. doi: 10.1002/mrm.10619. [DOI] [PubMed] [Google Scholar]
- 21.Bottomley PA, Ouwerkerk R. BIRP, an improved implementation of low-angle adiabatic (BIR-4) excitation pulses. J Magn Reson Ser A. 1993;103:242–244. [Google Scholar]
- 22.Volz S, Nöth U, Deichmann R. Correction of systematic errors in quantitative proton density mapping. Magnetic Resonance in Medicine. 2012;68:74–85. doi: 10.1002/mrm.23206. [DOI] [PubMed] [Google Scholar]
- 23.Wansapura JP, Holland SK, Dunn RS, Ball WS. NMR relaxation times in the human brain at 3.0 tesla. Journal of Magnetic Resonance Imaging. 1999;9:531–538. doi: 10.1002/(sici)1522-2586(199904)9:4<531::aid-jmri4>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]
- 24.Ethofer T, Mader I, Seeger U, Helms G, Erb M, Grodd W, Ludolph A, Klose U. Comparison of longitudinal metabolite relaxation times in different regions of the human brain at 1.5 and 3 Tesla. Magnetic Resonance in Medicine. 2003;50:1296–1301. doi: 10.1002/mrm.10640. [DOI] [PubMed] [Google Scholar]
- 25.Stanisz GJ, Odrobina EE, Pun J, Escaravage M, Graham SJ, Bronskill MJ, Henkelman RM. T1,T2 relaxation and magnetization transfer in tissue at 3T. Magnetic Resonance in Medicine. 2005;54:507–512. doi: 10.1002/mrm.20605. [DOI] [PubMed] [Google Scholar]
- 26.Deoni SCL. High-resolution T1 mapping of the brain at 3T with driven equilibrium single pulse observation of T1 with high-speed incorporation of RF field inhomogeneities (DESPOT1-HIFI) Journal of Magnetic Resonance Imaging. 2007;26:1106–1111. doi: 10.1002/jmri.21130. [DOI] [PubMed] [Google Scholar]
- 27.Gelman N, Gorell JM, Barker PB, Savage RM, Spickler EM, Windham JP, Knight RA. MR Imaging of Human Brain at 3.0 T: Preliminary Report on Transverse Relaxation Rates and Relation to Estimated Iron Content. Radiology. 1999;210:759–767. doi: 10.1148/radiology.210.3.r99fe41759. [DOI] [PubMed] [Google Scholar]
- 28.Yarnykh VL. Actual flip-angle imaging in the pulsed steady state: A method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magnetic Resonance in Medicine. 2007;57:192–200. doi: 10.1002/mrm.21120. [DOI] [PubMed] [Google Scholar]
- 29.Joseph PM, Axel L, O’Donnell M. Potential problems with selective pulses in NMR imaging systems. Medical physics. 1984;11:772. doi: 10.1118/1.595579. [DOI] [PubMed] [Google Scholar]
- 30.Schär M, Vonken E-J, Stuber M. Simultaneous B0- and B1+-Map acquisition for fast localized shim, frequency, and RF power determination in the heart at 3 T. Magnetic Resonance in Medicine. 2010;63:419–426. doi: 10.1002/mrm.22234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Edelstein WA, Bottomley PA. Method of three-dimensional NMR imaging using selective excitation, in. Google Patents. :1984. [Google Scholar]
- 32.Crawley AP, Henkelman RM. A comparison of one-shot and recovery methods in T1 imaging. Magnetic Resonance in Medicine. 1988;7:23–34. doi: 10.1002/mrm.1910070104. [DOI] [PubMed] [Google Scholar]
- 33.Cheng HLM, Wright GA. Rapid high-resolution T1 mapping by variable flip angles: Accurate and precise measurements in the presence of radiofrequency field inhomogeneity. Magnetic Resonance in Medicine. 2006;55:566–574. doi: 10.1002/mrm.20791. [DOI] [PubMed] [Google Scholar]
- 34.Hurley SA, Yarnykh VL, Johnson KM, Field AS, Alexander AL, Samsonov AA. Simultaneous variable flip angle-actual flip angle imaging method for improved accuracy and precision of three-dimensional T1 and B1 measurements. Magnetic Resonance in Medicine. 2012;68:54–64. doi: 10.1002/mrm.23199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hinshaw WS. Image formation by nuclear magnetic resonance: The sensitive‐point method. Journal of Applied Physics. 1976;47:3709–3721. [Google Scholar]
- 36.Carr HY. Steady-State Free Precession in Nuclear Magnetic Resonance. Physical Review. 1958;112:1693–1701. [Google Scholar]
- 37.El-Sharkawy A-MM, Qian D, Bottomley PA, Edelstein WA. A multichannel, real-time MRI RF power monitor for independent SAR determination. Medical physics. 2012;39:2334. doi: 10.1118/1.3700169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Venkatesan R, Lin W, Haacke EM. Accurate determination of spin-density and T1 in the presence of RF-field inhomogeneities and flip-angle miscalibration. Magnetic Resonance in Medicine. 1998;40:592–602. doi: 10.1002/mrm.1910400412. [DOI] [PubMed] [Google Scholar]
- 39.Gras V, Abbas Z, Shah NJ. Spoiled FLASH MRI with slice selective excitation: Signal equation with a correction term. Concepts in Magnetic Resonance Part A. 2013;42:89–100. [Google Scholar]