Modelling the evolution of a bi-partite network Peer referral in interlocking directorates

Abstract

A central part of relational ties between social actors are constituted by shared affiliations and events. The action of joint participation reinforces personal ties between social actors as well as mutually shared values and norms that in turn perpetuate the patterns of social action that define groups. Therefore the study of bipartite networks is central to social science. Furthermore, the dynamics of these processes suggests that bipartite networks should not be considered static structures but rather be studied over time. In order to model the evolution of bipartite networks empirically we introduce a class of models and a Bayesian inference scheme that extends previous stochastic actor-oriented models for unimodal graphs. Contemporary research on interlocking directorates provides an area of research in which it seems reasonable to apply the model. Specifically, we address the question of how tie formation, i.e. director recruitment, contributes to the structural properties of the interlocking directorate network. For boards of directors on the Stockholm stock exchange we propose that a prolific mechanism in tie formation is that of peer referral. The results indicate that such a mechanism is present, generating multiple interlocks between boards.

1. Introduction

A bipartite network defines a graph on a node set that represents two distinct types of social entities and where there may be relational ties only between nodes that are of different types. The social entities may be individuals and social clubs, authors and journal articles, directors and corporate boards, etc. Since bipartite networks make the conceptual link between social actors and social groups explicit, the study of bipartite networks is of great theoretical importance for understanding the duality of persons and groups (Breiger 1974; Doreian 1979; Feld 1981; Freeman and White 1993; Pattison and Robins 2002). The nodes and ties in bipartite networks may be researchers citing papers (e.g., Small 1973); people participating in social events (Breiger 1974); partners in crime (Frank and Carrington 2007); or directors on corporate boards (Mizruchi 1996). This paper is focused on the last case, directors and boards. A so called interlocking directorate is a bipartite board to director network consisting of vertices representing corporate boards and directors. A tie exist between board i and director j if j is a member of board i.

Most previous research on bipartite networks has focused on one of the two unimodal networks where two nodes of one type are considered tied if they share at least one alter of the other type. The obvious benefit is that methods developed for the analysis of unimodal networks applies. But as pointed out by Robins and Alexander (2004), the duality in defining for example the individuals by their affiliations with certain events or in defining the events by their ties to individuals, makes it hard to give priority to one type of node over another (Breiger 1974; Galaskiewicz et al. 1985; Breiger and Pattison 1986). Transforming a bipartite network to a unimodal network always means a loss of information (Borgatti and Everett 1997). In particular, the strength of a tie is lost if we ignore the number of nodes of one type that two nodes of another type share. It can also be shown that a completely random bipartite network may give rise to quite interesting but altogether spurious structural features in the unimodal representations (see also Newman et al. 2001).

Because of the inherent dynamic nature of social networks, a wide variety of statistical models have been proposed for studying network evolution over time. While several methods assume that changes are made in discrete steps from one moment to the next (Katz and Proctor 1959; Wasserman and Iacobucci 1988; Sanil et al. 1995; Robins and Pattison 2001), considerable advantages may be had from modelling longitudinal social networks in continuous time (cf Snijders, 1996, 2001). The early models for longitudinal social networks using continuous-time Markov chains (Holland and Leinhardt 1977; 1977; Wasserman 1980; 1980; Leenders 1995) built on the assumption that the dyads evolved independent of each other, which excludes the exploration of dependencies on larger structures than the dyad. In response to this Snijders proposed a flexible and empirically testable class of stochastic actor-oriented (or actor-based) models that draw on the assumption that actors strive towards organising their social ties in a utility maximizing manner (Snijders and van Duijn 1997; Snijders 2001; 2005; 2006).

However, so far the evolutionary network models have not been adapted to the study of the evolution of bipartite networks, although there are some longitudinal studies of the evolution of interlocking directorates. Galaskiewicz and Wasserman (1981) fit a discrete-time model to the unimodal corporate network implied by interlocks in a small bipartite network. Like previously proposed models it also assumed dyad-independence. In their study they focused primarily on the corporations and they distinguished between different industries and used a qualified version of board membership that gives directed interlocks. Mizruchi and Stearns (1988) model the appointment of financial directors on non-financial boards for a small selection of boards. Studying the dichotomous event “hiring” or analysing the evolution of the induced unimodal network, prevents investigation of the strength of interlocks. Similarly, in these two models changes are largely explained through corporate specific covariates (size, solvency, profitability, etc) rather than in terms of structural aspects of the bipartite (and unimodal) network(-s), i.e., endogenous self organising principles.

Here we propose a model for studying the evolution of bipartite networks that draws on Snijders’ work on stochastic-actor networks. We analyse data on corporate boards for all firms traded on the Stockholm Stock Exchange’s primary list between 1996 and 2005 (Edling and Sandell 2001; Bohman 2006). In our application, we focus on the processes of appointment to and departure of directors from boards based on a theory of action in the context of interlocking directorates. Central to this concept is the occurrence of multiple interlocks, which we elaborate on in section 3.

We proceed by describing the statistical model. This is first done using a general model formulation with an inference strategy for the evolution of bipartite graphs that follows the model proposed in Koskinen and Edling (2004) that is in turn an extension of the stochastic actor-oriented models for directed unimodal graphs of Snijders (2001). We then discuss peer referral in interlocking directorates, in section 3, before detailing the modifications needed for analysing interlocking directors in section 4. We then fit models with structural features and with additional controls for director attributes in section 5. To test the goodness of fit for the model, in section 6 we compare forecasts from the model with observed data. We finish the paper with some concluding remarks.

2. Model formulation and estimation

We consider a bipartite graph on a fixed vertex set V that is the union of two disjoint subsets A and B, m =| A |, n =| B |. We denote by N the subset of pairs of vertices that constitute the set of possible relational ties between vertices. In the case of a bipartite graph N = A × B , there can only be ties between vertices from different classes. The aim is to model the evolution through time of the random set of edges E ⊆ N . The (generalised) adjacency matrix is a collection x = (x_e : e ∈ N) of | N |= nm tie-variables 1{e ∈ E}, indicating whether the tie is present or not, and we denote by X the space of all possible realisations of x. For x, y ∈ X we define the Hamming metric as

$$\Vert x-y\Vert ={\displaystyle {\sum }_e\left|x_e-y_e\right|.}$$

The model is a continuous-time Markov chain {x(t)}_t∈R on X , which may be defined in terms of its embedded chain (or walk on the | N | -cube) as in Koskinen and Snijders (2007). The transition probabilities in the embedded chain are given by a function

$$\eta (\theta ,x,y)$$ (1)

and the time spent in x ∈ X exponentially distributed with rate function

$$\lambda (\theta ,x)$$ (2)

where θ is a vector of parameters. It is assumed that η(θ, x, y) ≥ 0 for ‖x − y‖= 1 and 0 otherwise. If we let Δ_ex denote the array that has element e equal to 1 − x_e but that is equal to x for all other elements, e* ∈ N \ {e}, the process may be described as remaining in a state x for a period of time that is exponentially distributed, after which element e is changed to 1 − x_e with probability η(θ, x, Δ_ex). For a digraph with N = V⁽²⁾ this is exactly the way the stochastic actor-oriented model for unimodal graphs is defined in Snijders (2001) for the purpose of simulation.

This is a framework that covers a wide variety of different models for network evolution. The expression ⁽¹⁾ can often be described with a logistic function, derived from evaluation of utility functions, and Snijders (2006) showed how many models of network evolution may be couched in the form of stochastic actor-oriented models. To express the bipartite evolution model in terms of an actor-oriented model we follow Koskinen and Edling (2004) and make the assumption that only vertices in A are considered to be actors so that given that a change is made, it is one of the vertices in A, say i, that decides to make a change, and if i changes its relation to j there is a jump from x to Δ_ijx (we use ij as a notational shorthand for (i,j)).

In the standard stochastic actor-oriented model (Snijders 2001), all actors i independently make changes at a rate λ_i(θ, x), given the current state x. This gives the rate (2) as $\lambda (\theta ,x)={\displaystyle {\sum }_i{\lambda }_i(\theta ,x)}$. Using well-known properties of the exponential distribution it can be shown that, given that a change is made, the probability that it is actor i that makes this change is λ_i(θ, x) / λ(θ, x). Consequently, we may express (1) as a product

$$\eta (\theta ,x,{\mathrm{\Delta }}_{\mathit{\text{ij}}}x)=\frac{{\lambda }_i(\theta ,x)}{\lambda (\theta ,x)}{p}_i(\theta ,x,j),$$

where

$$p_i(\theta ,x,j)$$ (3)

is the conditional probability that the process is going to jump from x to Δ_ijx, given that a change is made to ${(x_{\mathit{\text{ij}}})}_{j=1}^m$ for i fixed.

Figure 2.

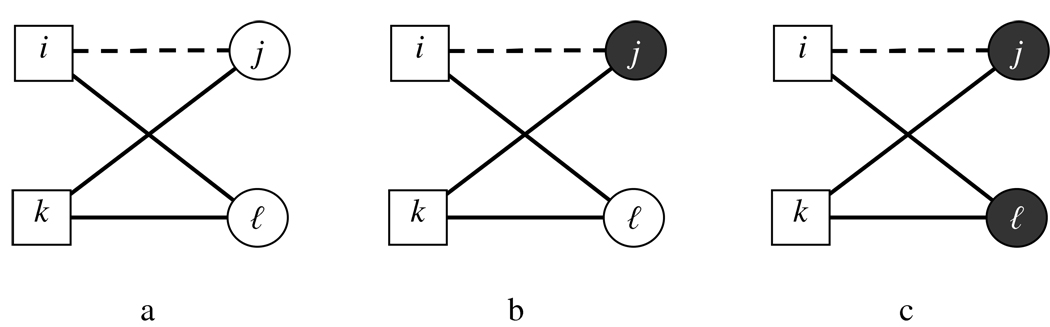
Bipartite attribute dependent configurations and the removal/creation of the tie {i,j}. Structures including dashed tie where dark (director) node indicates node having attribute and light node indicates absence of attribute. For attribute being female (W) labels are: (a) male homogenous 4-cycle (C_MM); (b) heterogeneous 4-cycle (C_MW); (c) female homogenous 4-cycle (C_WW);

Given that actor i makes a change, i changes the relation to j ∈ B , such that the “utility” u_i (θ, x, j,t) is maximised. The “utility” u_i (θ, x, j,t) captures the desirability to i of changing x_ij , of going from x to Δ_ijx. The stochastic actor-oriented framework for network evolution allows for many aspects of the change to be taken into consideration (Snijders et al. 2007) but we settle for a simple form

$$u_i(\theta ,x,j,t)=f_i(\theta ,{\mathrm{\Delta }}_{\mathit{\text{ij}}}x,x)+{\epsilon }_i(x,j,t),$$

where the first term on the right hand side is a systematic component and the second, ε_i(x, j,t), is a random component. The systematic part of the utility function represents what we model and is meant to capture the regularities in the data. The random components represent the non-systematic chance aspects of the decision situation that we do not explicitly model. Typically these are assumed to be independently identically distributed according to a type 1 extreme value distribution¹, which is a convenient choice for which a form of ⁽³⁾ is computationally equivalent to a conditional logistic regression.

2.1. Estimation

Given T realisations x(t₀), x(t₁),…,x(t_T−1) from the model defined by (1) and (2), the purpose is to perform inference for the model parameters θ. In describing this process we may without loss of generality assume that we only have two observations, x(t₀) and x(t₁), since the Markov property means that we may treat each pair of observations separately.

In order to write the likelihood function for θ given x(t₀) and x(t₁), let y = y(s₀), y(s₁), y(s₂),…,y(s_H+2k) be a realisation of the evolution from x(t₀) to x(t₁). Note that if y(s_H+2k) = x(t₁) and y(s₀) = x(t₀), for H =‖ x(t₀) − x(t₁) ‖, the number of changes must be H + 2k, for k ∈ {0,1,2,…}, because when the H necessary changes have been made to transform x(t₀) into x(t₁), any extra k unnecessary changes have to be reversed. Had a path y been observed then the likelihood function would have been given by

$$L(\theta ;y)=\text{exp}\left\{-{\displaystyle \sum _{h=1}^{H+2k+1}(s_h-s_{h-1})\lambda (\theta ,y(s_{h-1}))}\right\}{\displaystyle \prod _{h=1}^{H+2k}\eta (\theta ,y(s_{h-1}),y(s_h))\lambda (\theta ,y(s_{h-1}))}$$ (4)

where s_H+2k+1 = t₁. The likelihood given observed data, the observed data likelihood, is obtained when (4) is marginalised with respect to y, conditional on the endpoints x(t₀) and x(t₁). From a Bayesian perspective, all relevant information about the model parameters is given by the posterior distribution, π(θ| x(t₀), x(t₁)), and with constant prior distributions it is proportional to the observed data likelihood. In this case, neither the posterior distribution nor the observed data likelihood, are analytically tractable. We may however simulate from the joint posterior π(θ, y | x (t₀), x(t₁)) which is proportional to (4) (multiplied by a proper prior distribution π(θ) if available). A sample from this distribution may be obtained using Markov chain Monte Carlo (MCMC) by creating a Markov chain that alternates between drawing from π(θ| y) and π(y | θ, x(t₀), x(t₁)), both of which are proportional to (4) (for details see Koskinen and Snijders 2007).

We return to model estimation in section 4, when applying this model to analyse peer referral in interlocking directorates.

3. Interlocking directorates and peer referral -The action mechanism

This section presents an action mechanism for the actor-oriented model of network evolution. We specify and interpret the model based on two interacting mechanisms: peer referral and homosociality (or cognitive gender homophily). Before we discuss these mechanisms, we wish to briefly underscore the importance of explicitly considering the bi-partite structure in the analysis of interlocking directorates.

One can easily transform a bipartite board-to-director network into two one-mode symmetric networks: The inter-personal, director-to-director network consists of the directors and the ties between them. Two directors share a tie if they are members of the same board. Similarly, in the board-to-board network, the boards are the vertices and there are ties between pairs of boards that share a board member. However, some important information is lost by such transformations.

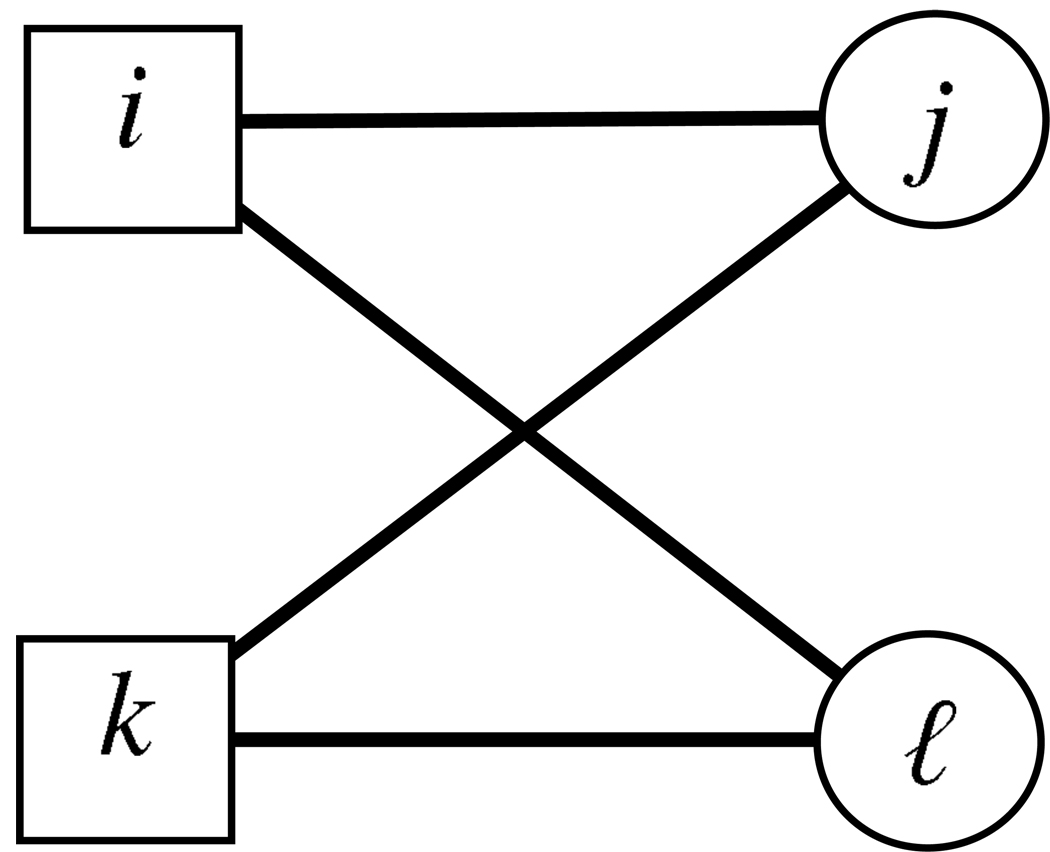
The multiple interlock as illustrated in Figure 1 (C₄) occurs when two boards of directors share (at least) two directors (also four-cycle, Pattison and Robins, 2002; Wang et al., 2009; or (2,2) biclique, Borgatti and Everett, 1997). In the following graphs circles and squares correspond to directors and boards respectively and a line connecting a director with a board means that the director is a member of the board. If any one of the ties, say {i,j}, are missing from the subgraph in Figure 1, the board i is only indirectly linked to j through a path of length 3. We refer to this structure as a (bipartite) three-path (L₃). Should director j be appointed to the board i, such that the tie {i,j} is created, the three-path is transformed into the four-cycle depicted in the figure. The addition of this edge does not alter any of the one-mode networks as the two directors were already connected through the other board and the two boards were connected through the director that sat on both boards. Thus in terms of the two one-mode networks these two subgraphs L₃ and C₄ are equivalent.

Figure 1.

A four-cycle (C₄): multiple overlaps create a multiple tie between board i and board k.

Most analyses of interlocking directorates have focused on the one-mode (binary) representations, and multiple interlocks (i.e. instances of C₄) have in general not been distinguished from single interlocks. The reason for not investigating multiple interlocks can stem from the choice of model (e.g., Mizruchi and Stearns 1988), or lack of data (e.g., Barnes and Ritter 2001). However, a small number of studies focus specifically on the prevalence of multiple interlocks, in particular the broken tie literature (Ornstein 1982; Palmer 1983; Ornstein 1984). Whereas these early studies found that a severed interlock was more likely to be replaced if this interlock was part of a multiple interlock, Palmer et al. (1986) suggested that this association was spurious and that the true determinant was the level of embeddedness. They referred to the production of an interlock that corresponds to the transition from a three-path to a four-cycle as “reinforcement”. The process of reinforcing already present ties between boards as an expression of the firms’ embeddedness can also be taken down to the level of directors. Whereas we focus on the social process of board-to-board tie reinforcement, the phenomena has also gained some attention in corporate governance literatures, and the conclusion seems to be that mutual interlocks are not strategically motivated (Carpenter and Westphal 2001; Fich and White 2003; 2005).

Robins and Alexander (2004) mention personal referral as a possible process that lead to multiple interlocks. When a board is looking to appoint a new board member, a present member may recommend a person with whom he or she has had previous experience of working with on another board. If this personal referral is endorsed by the board a multiple interlock is created.

This practice can be expressed in terms of an action mechanism in which ego puts a preference on alter when it comes to recommending new directors to the board of which ego is a member. Explaining the formation of this preference goes beyond the scope of this paper, but we can suggest some plausible explanations worthy of future exploration. An obvious candidate is that directors have more first-hand information on directors whom they have worked with, and that they consider first-hand information more trustworthy than second-hand information. Another suggestion is that working together on a board give rise to as sense of community among board members that would make fellow board members first choice candidates for filling vacant positions. A related idea, assuming that multiple board assignments are attractive, is that directors who know each other from working together recommend each other reciprocally. A more sophisticated explanation could be that directors are bound by silent agreements and codes of conduct stemming from a sense of membership in collectives such as “old boy’s networks” and “inner circles” (Mills 1956; Useem 1984) that tell them to look out for their peers.

Applying the mechanism of peer referral, the interlock itself (manifested by the 2-star) is not desirable for the firm. The interlock may be desirable to the director who acts merely as an unconstrained individual or to the board that acts as a collective representing a firm that strives to be central (for purposes of information gathering or for other purposes) in the board-to-board network. Boards and directors are also unlikely to strive towards establishing reach in the bipartite network as manifested in a desire to create 3-paths. If peer referral of co-members is expressing the individual action constrained by the setting and informed by group norms, then it is a mechanism that is central to the evolution of the network. The empirical manifestation of this action mechanism is the creation of four-cycles and, on the network level, a high bipartite clustering. The clustering one might observe in the two unimodal networks, as manifested in triangulation as well as short pathways, are emergent features of the processes in operation in the bipartite evolution. Perpetuating these behaviours reinforces the norms behind it – these are part of the dynamics, the mechanism is both the cause and the effect.

Naturally, personal referral does not necessarily result in four-cycles in the board-to director network. A board member may well recommend a person on other grounds than that they have worked together on another board, and the recommended person might not be a member of the (relevant) population. Underlying social structures are important in the recruiting process.

If peer referral is indeed a central mechanism to the evolution of the network this may reflect underlying allegiances in which, we may hypothesis, women are not included. If women are not part of the old boy’s networks and not generally treated as peers by men we would expect that the recruitment of women does not follow the same rules as for men (e.g., Izraeli and Talmud 1997). This would then manifest itself in a low frequency of peer referrals that involved women. In order to investigate this we may distinguish different types of four-cycles.

In Figure 2 there are three types of four cycles that may result from ℓ referring j. In Figure 2a a man is referring another man creating what may be termed a male-homogeneous four-cycle. In Figure 2c a woman is referring another woman creating what may be termed a female-homogeneous four-cycle. An example of a heterogeneous four-cycle is given in Figure 2b, where a man refers a woman. When women are not included in the peer practices outlined above we expect instances of heterogeneous four-cycles to be rare. In our data there is not enough information to fully separate the different four-cycles wherefore we settle for including the interaction effect of women and four-cycles, essentially counting the number of structures (b) and (c) in Figure 2. The mirror image of (b), where a male is referred by a woman we deem to be of little interest and too rare to be empirically testable.

If there is a negative tendency towards creating heterogeneous four-cycles, this is exactly an example of how “homosocial reproduction” operates - men prefer to socialise with men and promote other men (Kanter 1977; Stafsudd 2006). If homosocial reproduction drives the evolution indicating that women are excluded from the peer practices of the boards this may well indicate further imbalances.

To parse out whether peer referral is indeed an active mechanism or whether the prevalence of four-cycles is simply a result of accumulative interlocks requires a dynamic model. We furthermore need to distinguish between preservation of multiple ties and the creation of multiple ties, the latter which indicates peer referral. If the mechanisms investigated here are active and if their application is reinforced through repeated use, then this is a process through time. If cross sectional snap-shots were investigated it would not be possible to say whether peer referral is a key ingredient in board appointments or if higher than expected number of four-cycles at each cross-section is simply inherited from previous time-points. The process is also by definition dynamic since the actions of the individuals within the board are not independent of their environment, the context. The action by one board furthermore reshapes the context for other boards.

4. Modelling and estimating peer referral in interlocking directorates

Before we define the specific forms of (1) and (2), given in section 2, the longitudinal study of interlocking directorates requires a few further modifications of the model specification. These are modifications that stem both from the nature of interlocking directorates as well as from computational considerations that have to be taken into account when dealing with large data sets.²

4.1. Agency

As argued in the previous section we observe actions taken by the boards but assume that this is the result of actions of individual directors making up the boards. For the purpose of fitting the model the board itself is considered the actor. Given a choice between allocating choice to board or directors the former seems more plausible. ³

Since it is assumed that the actors (now, boards) chose the course of action that maximises the utility to board, and that the maximisation is carried out over the entire set of actions, we also assume that the board is acting on perfect information. The random components allow for deviations from the systematic part of the utility function but the random component is assumed to be independent of model quantities and therefore it cannot be used to account for differential, fuzzy, knowledge of different “parts” of the decision space. The Markovian nature of the model assume that there is no strategic action in the sense that a board is prepared to take a loss now in order to gain in the future.

4.2. Differentiating between recruitment and release

Although we only aim at providing a rough approximation of the mechanism central to the evolution of the interlocking directorates, the difference in nature between recruiting a director and releasing a director has to be addressed (in the broken tie studies and in e.g. Mizruchi and Stearns, 1988, the initiation of a tie is clearly distinguished from the dissolution of a tie). We may for example expect that in many of the instances where a director leaves a board this is not a consequence of a choice on the part of the board but is more likely to be the result of retirement, illness, etc. To distinguish between the different processes, we let

$$f_i(\theta ,{\mathrm{\Delta }}_{\mathit{\text{ij}}}x,x)=\{\begin{array}{cc}{f}_{i,1}(\theta ,{\mathrm{\Delta }}_{\mathit{\text{ij}}}x),\hfill & \text{if}{x}_{\mathit{\text{ij}}}=1\hfill \\ f_{i,0}(\theta ,{\mathrm{\Delta }}_{\mathit{\text{ij}}}x)\hfill & \text{if}{x}_{\mathit{\text{ij}}}=0\hfill \end{array}.$$ (5)

This is akin to the gratification function in Snijders (2001), in that the satisfaction with a new state may depend on the previous state.

The number of seats on a board of directors is not likely to fluctuate much from year to year. To control for the effect of board size in the model outlined above would require a complicated rate function. This would also have to be combined with sensibly chosen functions of the board size in f_i (θ, Δ_ij x, x) but the differences in board sizes between boards, and the small number of choices for releasing a board member in comparison to the number of available choices leads to numerical instabilities.⁴ For the present data set for instance, a board in 1996 with 6 board members has 6 choices of directors to release and a choice of 1238 directors to recruit. To resolve this problem we introduce a binary random variable v_i (ϕ, x) that indicates whether the board i decide to recruit or release a director. This is included in the model as follows: given that i decide to make a change to the board composition ${(x_{\mathit{\text{ij}}})}_{j=1}^m$ and v_i (ϕ, x) = v, (3) is set to

$$p_{i,v}(\theta ,x,j)=\{\begin{array}{cc}\frac{\text{exp}(f_{i,v}(\theta ,{\mathrm{\Delta }}_{\mathit{\text{ij}}}x))}{{\displaystyle {\sum }_k\text{exp}(f_{i,v}(\theta ,{\mathrm{\Delta }}_{\mathit{\text{ik}}}x))1\{x_{\mathit{\text{ik}}}=v\}}},\hfill & \text{if}{x}_{\mathit{\text{ij}}}=v\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}.$$

The jump probabilities in (3) may now be written as mixtures

$$p_i(\theta ,x,j)=\text{Pr}\{v_i(\varphi ,x)=1\}{p}_{i,1}(\theta ,x,j)+(1-\text{Pr}\{v_i(\varphi ,x)=1\})p_{i,0}(\theta ,x,j).$$

We settle for a simple expression for the probabilities

$$\text{Pr}\{v_i(\varphi ,x)=1\}=\{\begin{array}{cc}\hfill \varphi ,\hfill & \hfill \text{if}{\displaystyle {\sum }_j{x}_{\mathit{\text{ij}}}>0}\hfill \\ \hfill 0,\hfill & \hfill \text{otherwise}\hfill \end{array}.$$

We are not going to specify the probabilities Pr{v_i (ϕ, x) = 1} any further since the corresponding variables are ancillary for the purpose of parameter inference in the estimation scheme (as we shall see further on).

4.3. Latent walk length

In the basic model formulation, given that x(t₀)changes into x(t₁), we know that at least H changes have taken place. In addition there might have been k ∈ {0,1,2,…} superfluous changes that were then reversed. For friendship networks it is plausible to assume that a number of such superfluous changes have been made but perhaps less so for interlocking directorates.⁵ We could introduce strong prior information to reflect the fact that we believe k to be small but the size of the data set makes it convenient to perform inference conditioned on k = 0. The consequences for inference are that we only need to employ “Move type 3” (in the terminology of Koskinen and Snijders, 2007, i.e. permuting the order of the changes) in the updating of latent walks and, that the probabilities Pr{v_i (ϕ, x) = 1} cancel in the evaluation of (4) for updating the latent walks.

As for all the models in the stochastic actor-oriented framework for network evolution, had the exact timing of the changes been observed sequential logistic regression could have been used (Butts 2008). In the case investigated here the exact times are however not available. In principle there are fixed points in time when the new boards are officially appointed⁶ (annual grand meetings) but (notwithstanding the fact that they are not recorded here) from a substantive point of view the decisions are not instantaneous. The process of appointment may be said to be one going on over a longer period of time, during which the search for directors goes on. The search for directors to nominate can take many expressions as it is not legally regulated (Bohman 2009). Sometimes, but far from always board nomination committees are used (ibid.). At the time of official endorsement by the shareholders the boards have already been de facto appointed (there are exceptions, instances when the annual grand meeting reject the recommendations by the board, but these are rare).

4.4. Data and boundary considerations

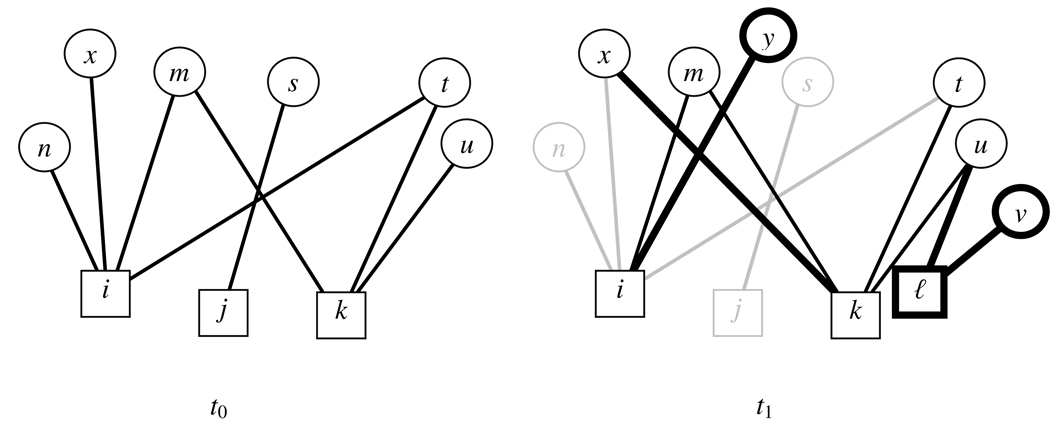
The definition of node sets when studying evolution of bipartite networks may depend on the application but in most cases the boundary specifications differ from those for unimodal network analysis. As an example of the difficulties in the longitudinal study of interlocking directorates consider the networks in Figure 3. There are two (hypothetical) realisations of a bipartite network at time t₀ and t₁, and for the two cross-sectional networks it is assumed that a node of either type can only be part of the network if it is tied to a node of another type. Tie dissolution and tie creation thus redefines the set of nodes (at t₁ greyed lines denotes ties or vertices that have disappeared and thick lines denotes ties or vertices that have appeared). There are 3 instances where ties are dissolved. When {i,n} is dissolved, n disappears from the bipartite graph since i is the only board n is a member of. The node t does not disappear when {i,t} is dissolved since t is also a member of board k. The node x is only a member of board i and consequently would have disappeared had the tie {k,x} not been created. The fact that {i,y} is created means that y is added to the population. If a node dies like j, it takes all nodes with it, like s, that are not tied to any other node. Analogously, the birth of a board may bring with it nodes that were not already part of the population, like in the case of {ℓ, v} and v.

Figure 3.

Boundary issues for the evolution of bipartite graphs: between t₀ and t₁, 4 ties have disappeared, 4 ties have been created, one board is born and one board has died. As a consequence and due to the fact that directors that are not on boards do not belong to the graph, 2 directors died and 2 were born.

We use what may be termed a pair-wise union rule, according to which for two points in time t₀ and t₁, the node set is considered to consist of all the nodes that are present at at least one of those occasions. By analysing the data for years pair-wise rather than for the entire period 1996–2005 we minimise the errors that may occur as a result of node set discrepancies as well as reduce the data down to a manageable size – the period 1996–2005 has 429 unique boards and 3177 unique directors but the largest network according to the union rule is 2001–2002 that has 306 boards and 1675 directors.

The population of boards necessarily changes over time as a result of mergers, acquisitions, businesses going out of business and the introduction of new corporations. The number of births and deaths each year are given in Table 1. For example we see that out of the 220 boards of corporations listed in 1996, 20 had died in 1997 and another 26 boards had been born. By the pair-wise union rule this means that the number of boards in the population in the period 1996–1997 is 220 + 26 = 246 and the size of the disjoint union is 220 − 20 = 200. Since 40 boards are born in 1998, the number of boards in the period 1997–1998 is 266.

Table 1.

Bipartite director degree distributions. The order of the degree distributions for a year is: when year used as t₁, original data (in bold face), when year used as t₀.

	deaths /births	Number of positions											Ave. pos
		0	1	2	3	4	5	6	7	8	9	10	Men	W	%W
1996	(220)	-	799	120	45	34	11	15	2	2	0	0	1.46	1.11	4.8
	23	216											1.21	0.93	4.7
1997	26	211											1.22	0.91	4.7
		-	796	129	47	27	14	12	7	1	0	0	1.47	1.19	4.3
	20	276											1.16	0.85	4.8
1998	40	173											1.27	1.02	4.8
		-	864	154	56	28	21	7	5	1	0	0	1.46	1.20	4.7
	20	291											1.16	0.88	5.1
1999	38	193											1.23	0.99	5.1
		-	965	147	58	32	21	6	4	1	0	0	1.42	1.24	4.7
	30	394											1.08	0.84	5.2
2000	44	262											1.14	1.11	5.2
		-	1085	172	49	38	11	7	4	0	0	0	1.36	1.27	5.5
	19	297											1.12	1.07	5.3
2001	33	227											1.17	1.18	5.3
		-	1137	183	64	28	16	3	1	3	0	1	1.36	1.27	5.7
	26	239											1.17	1.02	6.1
2002	17	311											1.11	1.22	6.1
		-	1063	188	61	27	12	8	2	2	1	0	1.38	1.37	6.7
	18	240											1.22	0.75	10.9
2003	3	273											1.11	1.32	10.9
		-	1042	188	51	28	11	8	3	0	0	0	1.35	1.39	12.6
	10	233											1.18	1.01	15.1
2004	5	231											1.13	1.25	15.1
		-	1050	182	55	28	8	6	2	1	1	0	1.35	1.37	16.3
	14	175											1.2	1.16	17.2
2005	4	213											1.14	1.19	17.2
			1023	173	66	17	7	5	3	1	0	0	1.34	1.33	18.0

The derived population of directors also changes as a result of board deaths and births as well as dissolution and creation of ties. The effect of the pair-wise union rule on the bipartite director degree distribution in Table 1. The degree distribution when the data for 1996 has been transformed according to the union rule is identical to the original data except for the number of directors without board positions, the number of directors with degree 0. These 216 individuals are the directors that are members of at least one corporate board in 1997 but not members of any board in 1996. The data at 1997 is augmented by 211 directors with zero degree when 1997 is used as the second time-point. These are the individuals that that are members of at least one corporate board in 1996 but not members of any board in 1997.

The percentage of female directors increases from 4.8% in 1996 to 18% in 2005. As an example of how the population of directors is affected by the pair-wise union rule consider the percentage of female directors in 1996 and in 1997, which is 4.8 and 4.3 respectively. Since all female directors that are board members for at least one time-point are included in the population for 1996–1997, the percentage of female directors in the data used is in-between, namely 4.7. The effects on the average number of board positions for men and women, respectively, from applying the pair-wise union rule are also given in Table 1, as are the bipartite director degree distributions for the original data and the transformed data

In some instances the pair-wise union rule may come with some drawbacks. Some director departures may in fact reflect board deaths rather than release of a director. Births of directors may involve something of a circular definition; if a director is not on any board in 1996 but on a board in 1997, the board may choose that director according to the model because this director is going to be chosen in the future by that board. It would be better to model births of directors separately and in principle it is straightforward to do so in the Bayesian framework but in view of parsimony we refrain from modelling this. An alternative would be to start only with directors that are board members. Huisman and Snijders (2003) deal with changing composition by letting the births and deaths of nodes be time-varying but exogenously defined events.

When a director retires, dies or in another way leaves the population altogether, this may mean the director leaves several board positions simultaneously, which violates the model assumptions and may introduce additional dependencies between the decision processes of the boards. This is likely to affect the dissolution process more than the appointment process.

4.5. Statistics

To define the systematic functions in (5), we introduce a set of parameters θ₁,…,θ_p, that are used to weight together counts z_i1 (x),…,z_ip (x) of configurations in a bipartite graph to determine the (systematic) contribution to the satisfaction of the board i with x. When differentiating between creating a tie and dissolving a tie, we may write

$$f_{i,v}(\theta ,{\mathrm{\Delta }}_{\mathit{\text{ij}}}x)={\theta }_{1,v}{z}_{i1,v}({\mathrm{\Delta }}_{\mathit{\text{ij}}}x)+\cdots +{\theta }_{p,v}{z}_{\mathit{\text{ip}},v}({\mathrm{\Delta }}_{\mathit{\text{ij}}}x)$$ (6)

where v = x_ij. The vector of parameters here is assumed to be unrestricted. When a parameter is positive this means that boards tend to prefer to make changes that lead to increases in (or preserves in the case of dissolution) the number of configurations corresponding to that parameter, given everything else.

In the case of cross-sectional data, the Markov assumptions of Frank and Strauss (1986), as applied to bipartite networks implies that the only sufficient statistics are the bipartite star statistics (Skvoretz and Faust 1999; Wang et al. 2009). Four-cycles may also be derived from social circuit outcome dependence assumptions (Snijders et al. 2006) as shown in Wang et al. (2009). Here our primary interest is in peer referral and the creation of four-cycles, which is why we let the four-cycle be one of the configurations we include in (6). As illustrated in Figure 4 (c), a four-cycle is created when a tie {i,j} is added by i to a three-cycle. If there is a positive coefficient corresponding to the number four-cycles for creating ties then we know that there is a preference for appointing directors that is consistent with peer-referral. If in addition the coefficient corresponding to the number of four-cycles for dissolving ties is zero or negative then we know that the preference for appointing directors that is consistent with peer-referral is not only an artefact of boards wanting to have strong ties to other boards. The systematic function is a linear function of the number of four-cycles (ceteris paribus) not primarily because the value of multiple interlocks is assumed to be additive but because there is a positive (negative) preference for recruiting a director if he or she has been referred by someone on the board. Occasionally, the addition of a tie may create more than one additional four-cycle and one may then ask if the effect in those cases should be additive – does it matter if a director is referred by more than one present director? Here we assume that it does but alternatives where only the sign (addition of four-cycle or not) is considered could well prove useful.

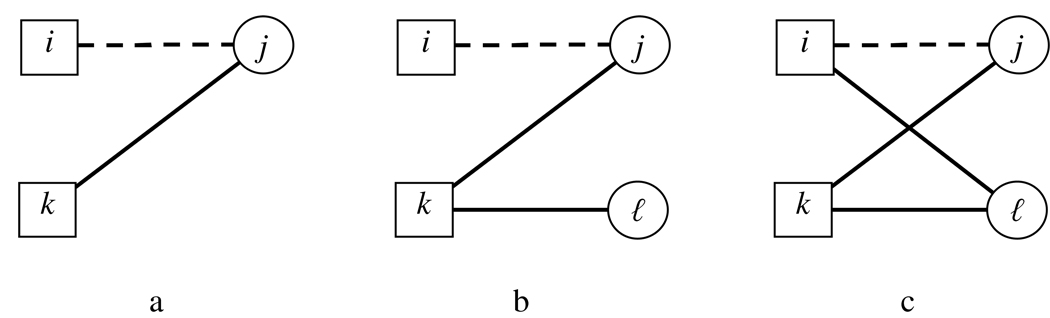
Figure 4.

Bipartite configurations and the removal/creation of the tie {i,j}. Structures including dashed tie: (a) bipartite director 2-star (S_B2); (b) bipartite 3-path (L₃); (b) bipartite 4-cycle (C₄).

The four-cycle is built up of bipartite director 2-stars (S_B2) (Figure 4a) and a bipartite 3-path (L₃) (Figure 4b). To ascertain that the preference for creating four-cycles is not merely due to a preference for establishing interlocks (S_B2) or long paths (L₃), we need to include counts of these as well. Some other counts described in Skvoretz and Faust (1999), Wang et al. (2009), and Robins and Alexander (2004) such as the number of edges and bipartite board two-stars are not relevant if we condition on walk length. For example, conditional on the event that the board is going to add a director, all potential new board members will yield the same contribution to the count of bipartite board 2-stars. The corresponding parameter is hence not estimable.

In a first model only the three structural features illustrated in Figure 4 are included. In a second model we also include several director attributes as covariates. In the cases where these are time-varying, they are defined in relation to time-points t₀ and t₁ for the relevant pair of years.

4.6. Covariates

Many studies have pointed to the importance of the relation between the corporate board and the CEO (Zajac and Westphal 1994; Fich and White 2003) for the performance of the board and the company. The position of CEO offers an opportunity for forging alliances and gaining experience and insight. Fich and White (2005) also put the focus on the overrepresentation of CEOs in multiple interlocks. Here we do not include any interaction for CEO and multiple interlocks but include an indicator of whether a director has any CEO experience. This covariate indicates if a director has been the CEO for a corporation for a year previous to the second time-point t₁.

We define chair experience in an analogous fashion to CEO experience, namely if a director has been chairman of a board in the year previous to the second time point. The chair has a central position in the board of directors and someone with chair experience may therefore be regarded as having insight into the corporations on which he or she has served. Having chairman experience may also signal status and add to one’s reputation.

Seniority may be important both as marker of position in status hierarchies as well as a control for natural demographic changes. Here we used age and to improve numerical stability, age is standardised for each time period.

The female representation on company boards has long been a hotly debated issue, and we have already alluded to the occurrence of and change in female board representation in the study period. But does increasing representation mean increasing interlocking when controlling for other factors? Are women fully integrated in the corporate structure and are they as powerful as men in terms of being central in the network? The indicator of whether a director is a woman or not also serves as the lower order term for the interaction effect of sex and four-cycles. As previously stated, the interaction term counts the number of structures corresponding to (b) and (c) in Figure 2.

5. Results

For setting initial parameter values and variance covariance matrix for the proposal distribution we followed Koskinen and Snijders (2007) and obtained the Hessian of and parameter values that maximised the likelihood for arbitrarily chosen shortest paths. The Metropolis-Hastings algorithm was implemented with a total of 4,000 iterations and a burn-in period of 1,000 iterations.

Summaries for the posterior of the purely structural model are given in Table 2 and comparisons of interval estimates are given in Figure 5. The processes of appointments and releases are quite different. Apart from a tendency to preserve three-paths in 1996–1997, there are no structural effects in the release.

Table 2.

Parameter estimates (posterior means and standard deviations) for longitudinal model fitted pairwise to corporate boards on the Stockholm stock exchange. Structural effects only.

	Effect
	Dissolution			Creation
	Dir. 2-star	3-path	4-cycle	Dir. 2-star	3-path	4-cycle
1996–1997	−0.409(0.159)	0.045(0.014)	0.052(0.073)	−0.477(0.205)	−0.002(0.016)	1.046(0.076)
1997–1998	0.219(0.266)	−0.022(0.023)	0.227(0.092)	−1.110(0.203)	0.021(0.017)	1.019(0.077)
1998–1999	−0.118(0.198)	0.014(0.017)	0.028(0.074)	−0.981(0.202)	0.012(0.017)	1.437(0.084)
1999–2000	−0.175(0.221)	0.017( 0.02)	0.162(0.117)	−0.896(0.256)	−0.039(0.022)	1.295(0.112)
2000–2001	−0.220(0.182)	0.023(0.017)	−0.096(0.115)	0.430(0.223)	−0.122(0.019)	1.509(0.109)
2001–2002	0.172(0.162)	−0.002(0.016)	0.182( 0.110)	−0.084(0.255)	−0.073(0.021)	1.685(0.087)
2002–2003	−0.058(0.181)	0.004(0.016)	0.047(0.089)	−2.390(0.522)	0.085(0.044)	1.220(0.102)
2003–2004	−0.309(0.352)	0.032( 0.030)	0.235(0.151)	−2.225(0.551)	0.063(0.044)	1.303(0.150)
2004–2005	−0.273(0.231)	0.023(0.022)	0.286(0.136)	−3.003( 0.460)	0.122(0.036)	1.626( 0.150)

Figure 5.

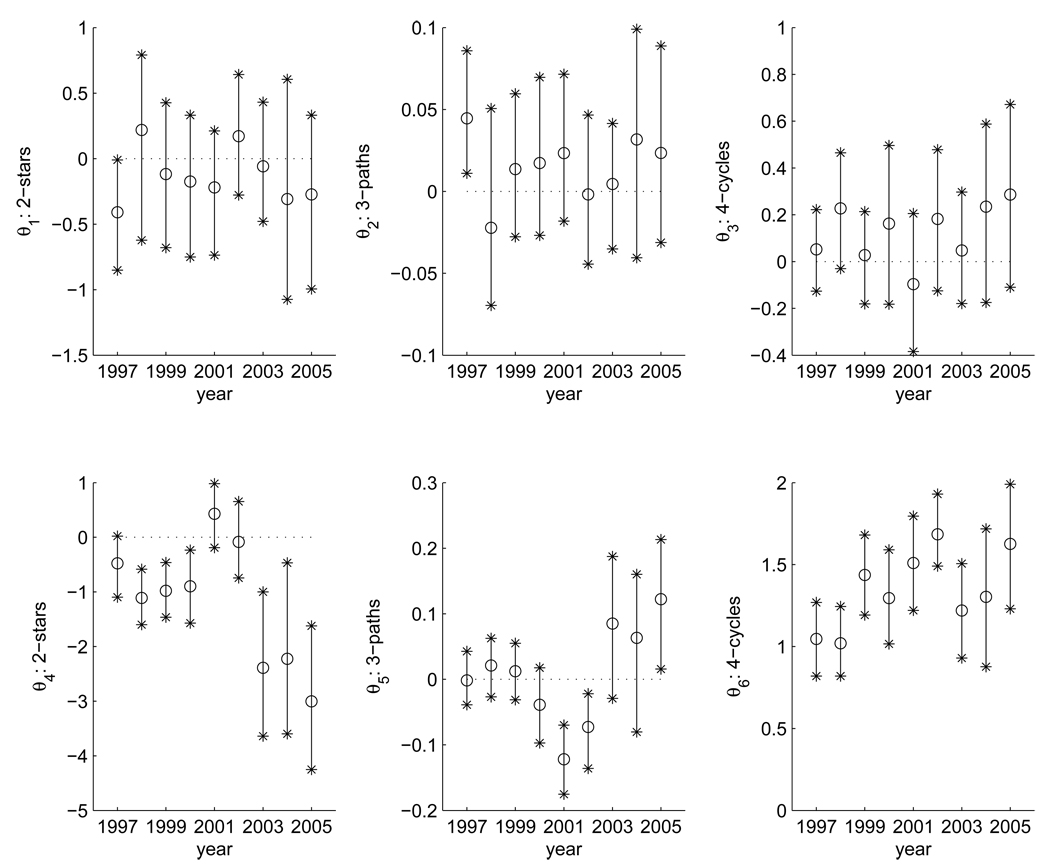
Probability intervals (.99 equal tail probability) for parameters across time in the purely structural model. Parameters θ₁ through θ₃ correspond to 2-stars (S_B2), three-paths (L₃), and four-cycles (C₄), for the dissolution of ties and parameters θ₄ through θ₆ correspond to 2-stars (S_B2), three-paths (L₃), and four-cyclews (C₄), for the creation of ties.

There is no desire (or an aversion in 2000–2002) to create bipartite director two-stars when recruiting directors, everything else given. Creating interlocks is thus not desirable to the board per se. Since the coefficient for three-paths is negative or zero there is no desire to link to boards (via directors) with many directors or desire to reach directors indirectly (to shorten path-ways in the bipartite graph in an efficient manner; it appears to be a negative effect in 2000–2001 and in 2001–2002 and a positive effect in 2004–2005, otherwise no effect).

There is a marked desire to create four-cycles and in combination with the fact that there is no tendency towards preserving four-cycles, this is strong evidence of peer referral operating.

While parameter estimates may not be directly comparable over time due to changes in network compositions, the trends in Figure 5, reveals that the evolution appears to go through three different phases. In 1996–2000 the model seems homogeneous with respect to the (negative) preference for interlocking directors (2-paths), three-paths and peer referrals; in 2000–2002, the clustering increases; in 2002–2005 the process returns to something resembling the first phase but with greater variation (less certainty in the parameter estimates).

Adding director attributes do not change the structural effects to any greater extent. Summaries of the posteriors for the model with director attributes are given in Table 3 for dissolution of ties and in Table 4 for creation of ties. Interval estimates for the parameters are given in Figure 6.

Table 3.

Parameter estimates (posterior means and standard deviations) for longitudinal model fitted pairwise to corporate boards on the Stockholm stock exchange. Structural effects, director attribute effects and the interaction of sex and peer referral for the dissolution of a tie.

	Effects Dissolution
	Dir. 2-star	3-path	4-cycle	CEO exp.	Chair exp	Seniority	Woman	Int. Wom. 4-cycle
1996–1997	−0.280(0.158)	0.033(0.013)	0.101(0.066)	0.276(0.151)	−0.043(0.168)	−0.093(0.070)	−0.234(0.283)	0.468(0.762)
1997–1998	0.230(0.151)	−0.023(0.013)	0.252(0.071)	0.579(0.173)	−0.003(0.151)	−0.130(0.074)	−0.042(0.321)	1.017(0.701)
1998–1999	−0.151(0.178)	0.017(0.014)	0.041(0.085)	0.118(0.148)	0.052(0.162)	−0.217(0.070)	−0.262(0.345)	−0.120(0.576)
1999–2000	−0.086(0.192)	0.009(0.018)	0.143(0.121)	−0.076(0.126)	−0.305(0.123)	−0.183(0.062)	0.290(0.433)	2.742(0.849)*
2000–2001	−0.092(0.222)	0.012(0.021)	−0.104(0.127)	0.000(0.158)	0.138(0.131)	−0.128(0.085)	0.501(0.299)	1.596(1.558)*
2001–2002	0.227(0.199)	−0.010(0.019)	0.214(0.101)	0.151(0.127)	−0.238(0.123)	−0.068(0.061)	−0.015(0.273)	1.268(1.873)
2002–2003	−0.075(0.206)	0.007(0.018)	0.067(0.118)	0.060(0.117)	0.050(0.133)	−0.267(0.058)	0.919(0.347)	1.349(0.977)
2003–2004	0.071(0.283)	0.002(0.024)	0.103(0.139)	−0.034(0.121)	0.162(0.165)	−0.352(0.073)	0.188(0.277)	5.605(2.887)*
2004–2005	−0.404(0.283)	0.035(0.025)	0.310(0.184)	−0.009(0.176)	0.198(0.189)	−0.130(0.077)	0.068(0.237)	0.089(0.375)

^*NB: indicates that marginal posterior improper

Table 4.

Parameter estimates (posterior means and standard deviations) for longitudinal model fitted pairwise to corporate boards on the Stockholm stock exchange. Structural effects, director attribute effects and the interaction of sex and peer referral for the creation of a tie.

	Effects Creation
	Dir. 2-star	3-path	4-cycle	CEO exp.	Chair exp	Seniority	Woman	Int. Wom. 4-cycle
1996–1997	−0.599(0.202)	0.008(0.017)	1.002(0.073)	−0.106(0.128)	0.359(0.183)	−0.247(0.046)	−0.270(0.240)	0.362(0.536)
1997–1998	−1.360(0.161)	0.048(0.014)	0.971(0.084)	−0.136(0.139)	0.663(0.131)	−0.219(0.048)	−0.208(0.217)	−0.698(0.801)
1998–1999	−0.796(0.288)	0.002(0.023)	1.354(0.090)	−0.532(0.177)	0.226(0.178)	−0.282(0.042)	−0.344(0.230)	0.429(0.413)
1999–2000	−0.554(0.198)	−0.063(0.019)	1.406(0.096)	−0.341(0.145)	0.106(0.154)	−0.347(0.045)	−0.033(0.189)	−0.111(0.639)
2000–2001	0.236(0.271)	−0.097(0.026)	1.527(0.096)	−0.501(0.147)	0.343(0.161)	−0.267(0.048)	−0.252(0.222)	−0.451(0.505)
2001–2002	−0.715(0.219)	−0.011(0.019)	1.662(0.089)	−0.359(0.148)	0.028(0.129)	−0.219(0.044)	0.373(0.171)	−0.721(0.709)
2002–2003	−1.698(0.382)	0.039(0.029)	1.163(0.110)	−0.141(0.128)	0.143(0.207)	−0.315(0.062)	0.866(0.119)	0.161(0.154)
2003–2004	−2.149(0.379)	0.066(0.029)	1.388(0.121)	−0.490(0.149)	0.059(0.227)	−0.302(0.050)	0.337(0.138)	−0.872(0.254)
2004–2005	−2.854(0.452)	0.114(0.037)	1.580(0.133)	−0.452(0.199)	0.139(0.179)	−0.220(0.063)	0.081(0.171)	−1.200(0.816)

Figure 6.

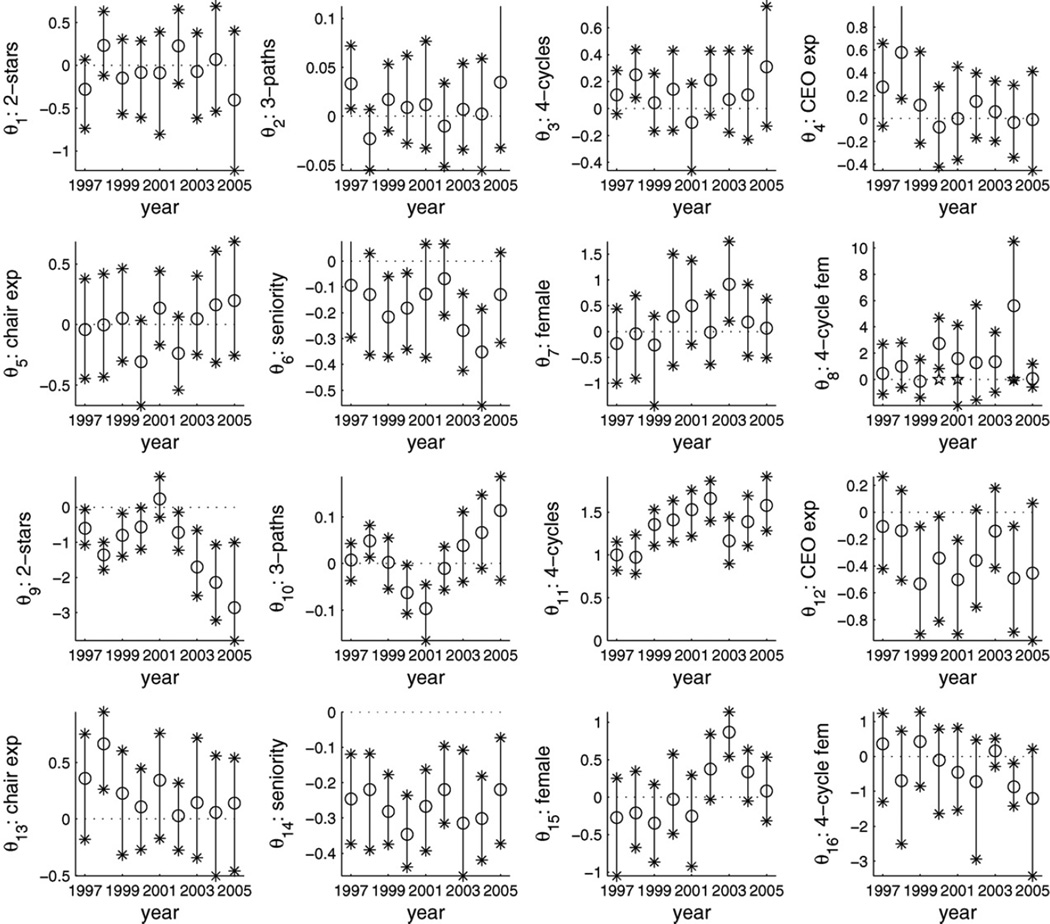
Probability intervals (.99 equal tail probability) for parameters across time in model with structural effects, director attributes and interaction between sex and peer referral

There is a positive CEO-effect for dissolution of ties in 1997–1998 but not in any other year suggesting that it is not of great importance to retain directors with CEO-experience. For four periods there is a negative CEO-effect on recruitment. Looking at the distribution of the number of board appointments for directors with and without CEO-experience (table not reproduced here) there is no clearly discernible difference other than that the proportion of directors with two or more seats is slightly larger for directors with CEO-experience and also that the proportion of isolate directors is higher for this group (at the second time-point). The latter means that many of the directors that leave the population have CEO-experience but few of the directors entering the population have CEO-experience (details may be obtained from the authors).

There is a consistent negative recruitment effect for seniority as well as for release in some periods. While there is a positive association between seniority and the number of board seats for most years cross-sectionally, the increase in the number of boards a director sit on is not positively related to age.

In 1997–1998 there is a positive effect for chair-experience but in other periods there is no attribute effect for having experience as chairman of the board.

There is no effect of sex in the period 1996–2001 but in 2001–2004 there seems to be a positive effect for recruitment (the .99-intervals just cover 0 in 2000–2001 and 2003–2004) and in 2002–2003 boards tend to want to keep female directors. This development is also reflected in Table 1, the transition from 2001 to 2002 is the year when the average number of board positions per women first reaches that of men. The following year there is also a preference for keeping these women, a tendency against firing women, which is reflected in the positive coefficient θ₇ in 2001–2002. Hence, in this period women hold more board positions than men on average. This is not explained by seniority, CEO or chairman-experience. As to how these women were recruited there seems to be a lot of uncertainty. There are not enough opportunities to create female interlocks since there were in general too few women (cf Table 1) and at the start of the series women accounted for too few ties (but from 2002 women occupy the same number of board seats as men on average).

The increased representation of women after 2001 is not accompanied by increasing peer referral. In fact, there is a tendency against referral of female directors in 2003–2004 – the posterior probability that the corresponding parameter is negative is practically 1 – and the following period the corresponding posterior probability is .95. We may tentatively conclude that while there is an increasing representation of women on the stock exchange, they are still not integrated in the male dominant power structures. Furthermore, the relative popularity of female directors is short-lived. We could speculate that there is an influx of token women in response to the threat of legislation.

We performed two robustness checks to assess the sensitivity of the model. To investigate the effects of the possible dependencies that may be induced by directors (permanently) leaving the population in a time interval, we fitted the model for each interval (t₀, t₁) excluding the directors that were isolates at t₁ (see Table 1). The differences in posteriors are overall small. For dissolution seniority in 1997-98 has a negative effect, and in 1999-00 and 2003-04 no effect; and there is too little information to infer anything for the interaction of female director and four-cycles. For recruitment the effect of CEO disappears in 1998-01 and 2003-04; chair experience becomes positive in 1996-98 and 1999-01; seniority has no effect in 2003-04; the effect for female directors edges up above 0 and the negative effect of the interaction of female director and four cycle weakens in 2003-04. While the average age of isolate directors at time t₁ is consistently .5 standard deviation units higher than at time t₀ (meaning that directors that leave the population are on average older than directors that enter the population) this does not explain the negative effect of seniority. The previously mentioned demographics do cause CEO experience to lose its effect when the isolates at the second time point are excluded.

6. Goodness of fit

We may use Bayesian forecasting to assess the goodness of fit of a stochastic actor-oriented model (Koskinen and Snijders, 2007). If the model is fit to observations x(t₀) and x(t₁) , a third observation x(t₂), which is not used in fitting the model, may be used for model evaluation. The idea is to asses how probable x(t₂)is given x(t₀) and x(t₁) , unconditional on the parameters. The distribution of x(t₂) given x(t₀) and x(t₁) is unconditional on the parameters is the posterior predictive distribution p(x(t₂) | x(t₀), x(t₁)). Assuming that the model is time-homogenous, the posterior predictive probability is given by

$$p(x(t_2)|x(t_0),x(t_1))={\displaystyle \int p(x(t_2)|\theta )\pi (\theta |x(t_0),x(t_1))}\mathrm{d}\theta ,$$ (7)

in which p( |θ) is the model defined by (4) marginalised with respect to the intermediate paths. It is very rarely possible to evaluate this integral analytically. Instead, we have to rely on Monte Carlo methods. In practice we simulate from the model for different parameter vectors, where we choose the parameter vectors in proportion to their posterior probability, their probability given x(t₀) and x(t₁). To choose these parameter vectors in proportion to their posterior probability we take the parameters from our posterior MCMC sample.

Predicting the individual elements of x(t₂)may not necessarily be very informative and therefore we choose to look at a variety of functions of the bipartite network, such as the one-mode degree distributions and bipartite clustering. Since the inference for θ given x(t₀)and x(t₁) was conditioned on the walk length and thereby the sum of the variables v_i (ϕ, x) for each i, the posterior predictive distribution is similarly conditioned on the number of changes per board and the number of these changes that involved recruiting or releasing a director. Note that when this approximation is used then the posterior predictive distribution does incorporate information about the observation that is being used for validations and hence the distribution is not strictly speaking a true posterior predictive distribution as in (7).

We chose the observations in 2002 and 2003 as our x(t₀) and x(t₁) and use the posterior conditional on these two observations to draw from our approximation of (7). The results for a collection of graph functions are given in Figures 9 and 10. For reference, the corresponding graph functions under a random walk are included. The random walk process is simulated in the same fashion as the posterior predictive distribution but with all parameters set to 0. This means that all sequences of changes that are concordant with the data structure are equally probable.

Figure 9.

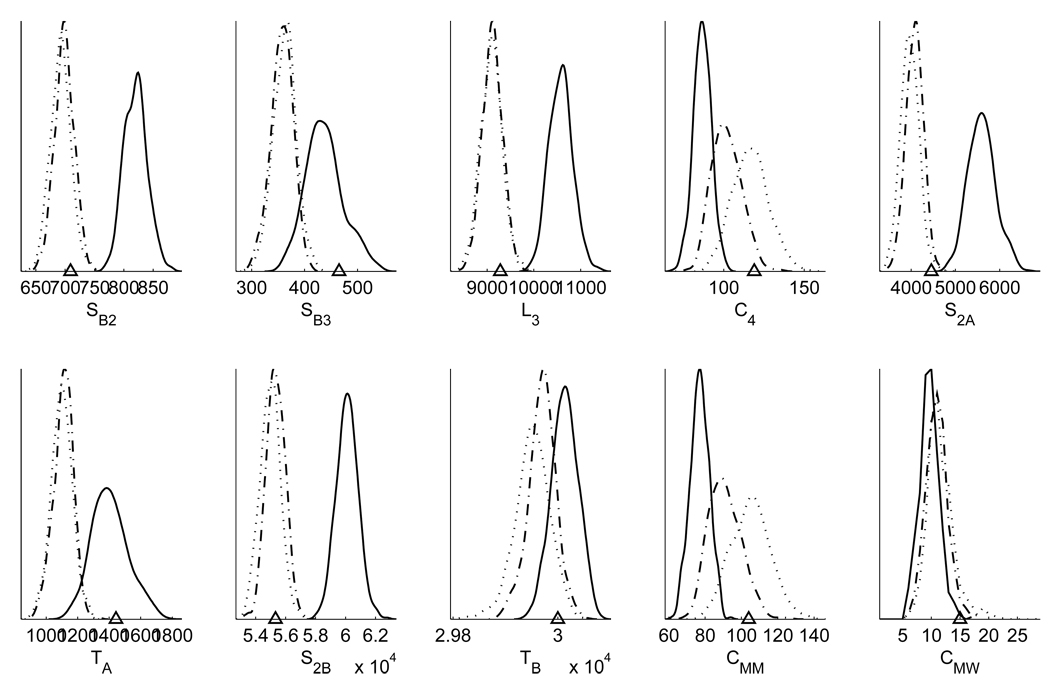
Posterior predictive distributions for bipartite graph counts: observed count in 2005 (triangle); (true) posterior predictive distribution given observations in 2003 and 2004 (dash dot); posterior predictive distribution using posterior distribution of model paramters conditional on given observations in 2004 and 2005 (dotted); base line distribution with all paramters set to 0 (solid).

Figure 10.

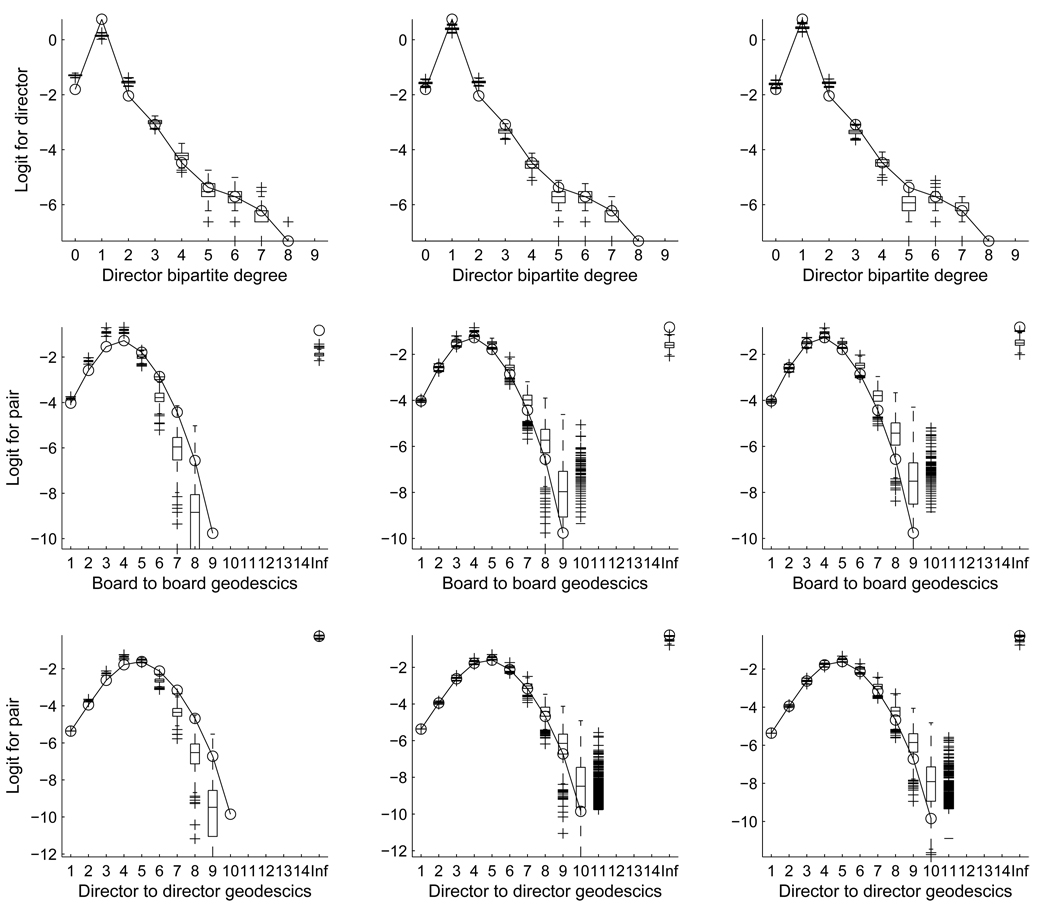
Posterior predictive distributions for bipartite director degree, unimodal board geodesic distribution, unimodal director geodesic distribution on logit scale. Observed distributions in 2005 (circle solid line); columns left to right: base line distribution with all parameters set to 0; (true) posterior predictive distribution given observations in 2003 and 2004; posterior predictive distribution using posterior distribution of model parameters conditional on given observations in 2004 and 2005.

We have fixed the board sizes and hence any variation in unimodal board triangles (T_A in Figure 7) is due to variation in overlapping director 2-stars (S_B2). Because of structural restrictions all three of the models capture the unimodal director clustering (i.e. T_B). In the case of the random walk the ability to replicate T_B is in some part due to over representing the number of unimodal director two-paths (S_2B, see Figure 8). Consequently, if we were to compare the ratio of the number of T_B to S_2B for the different models, and use that as a measure of the unimodal director clustering, then the random walk would not capture the unimodal clustering.

Figure 7.

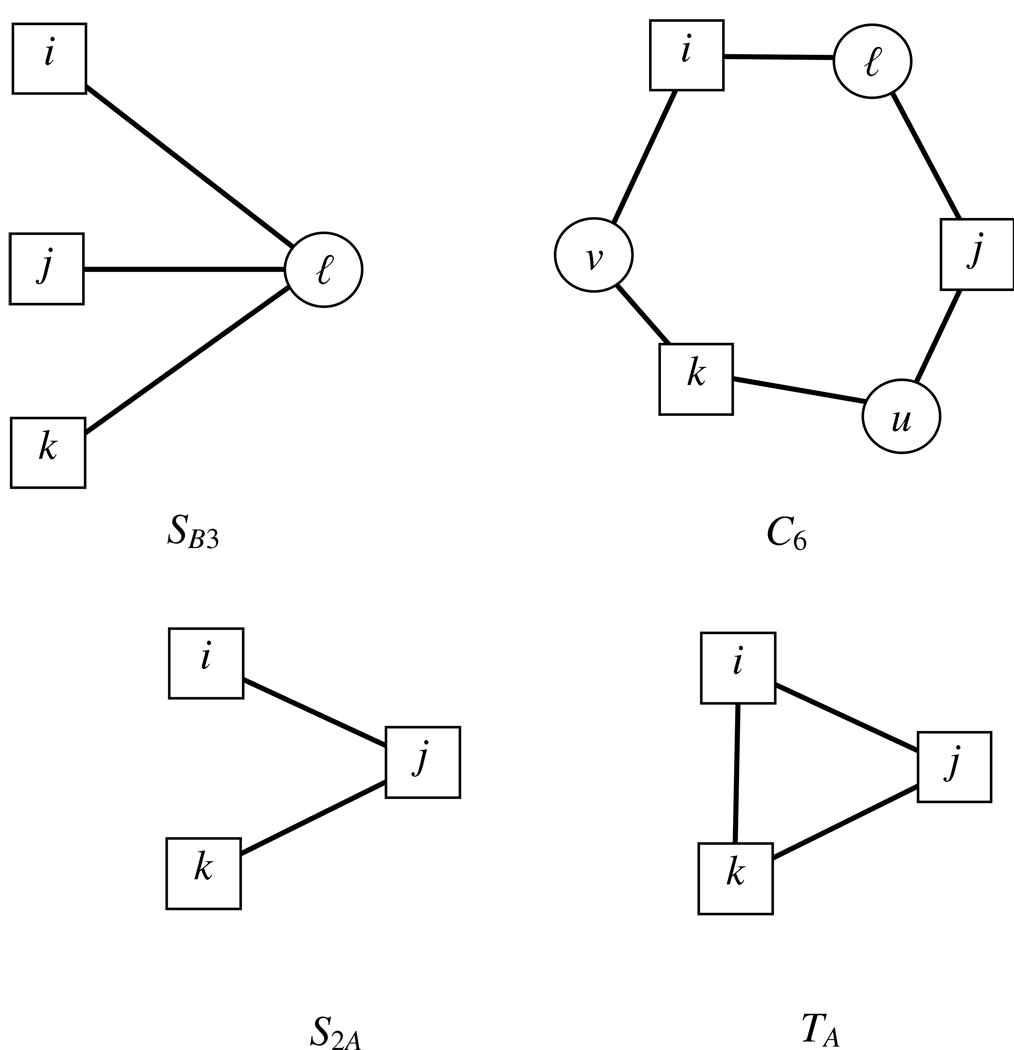
A bipartite director 3-star (S_B3), a bipartite 6-cycle (C₆), a unimodal board 2-star (S_2A), and unimodal board triangle (T_A).

Figure 8.

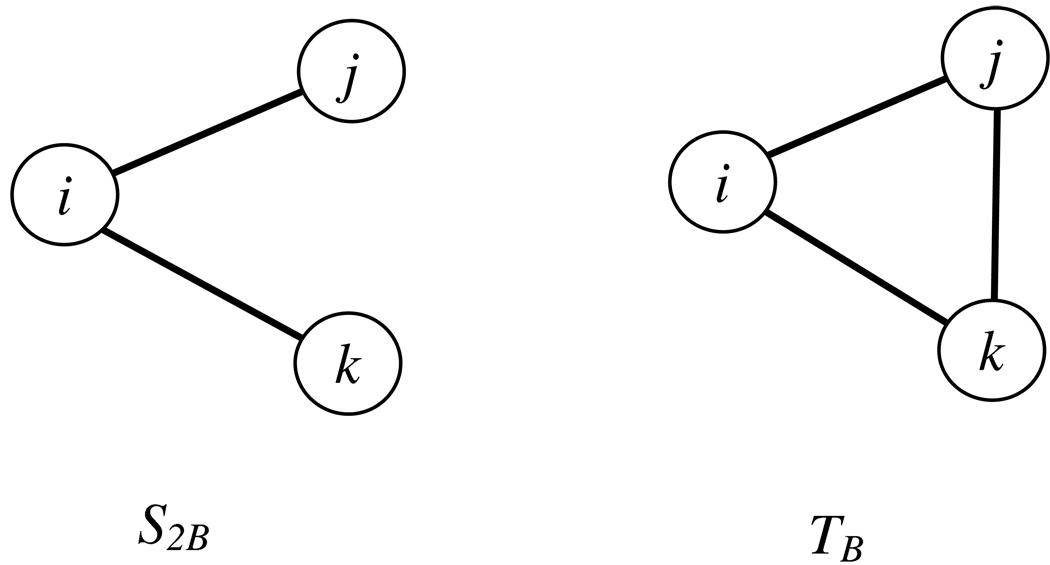
A unimodal director 2-star (S_2B), and unimodal director triangle (T_B).

The forecast makes an accurate prediction for the three-paths and four-cycles (Figure 9). The random walks severely overestimates the number of three-paths and underestimates the number of four-cycles which, using the definition of Robins and Alexander (2004), means that the bipartite clustering coefficient is underestimated.

As seen in Figure 9, the prediction model does not quite capture the number of S_B3 (and neither does the model estimated using 2005). The random walk more closely manages to capture the number of S_B3. As a result the random walk also captures unimodal board triangles (T_A) better but produces too many unimodal board two-stars (S_2A). Note that apart from directors that sit on many boards, S_B3, the other distinct underlying bipartite structure that yields T_A is a six-cycle, C₆. On the whole, the forecast, the random walk and the fitted model do an equally good job of predicting the bipartite-director degrees, or bipartite director stars, as seen in the top three panels of Figure 10.

We can claim to have captured the substantive element of T_A, unimodal board clustering. We could possibly have improved on the fit of S_B3 ’s but there is no substantive reason for including this in the model for a boards satisfaction with a new configuration and even less so for including six-cycles.

Thus, there is a clustering of boards that is unexplained by the model but that is likely to be the result of heterogeneity in the popularity of directors. By the popularity of a director we refer primarily to his or her actual number of board appointments. Differences in popularity may be explained by underlying peer groups or may be reflected in or reflected by status and prestige. Differential status and popularity could be captured by including further director attributes but there could also exist a self organising principle that explains status through reputation (Useem 1984; Kaplan and Reishus 1990; Zajac and Westphal 1994; Podolny 2005). Whether this status stems from the increased experience that comes with being central in the network or whether there was previously a peer dependent selection process so that multiple interlocks merely reflect high status and prestige in underlying social structures is an open question.

As an example of how well the model captures the other graph structures of the unimodal networks, we may compare the observed distribution of geodesic distances to the predicted (Figure 10). The model does surprisingly well but some thought must be given to the inherent structural restrictions on the unimodal representations. This is evident in the unimodal projections of the graphs produced by the random walk in that the geodesic distributions closely resemble data. The random walk does however fail in capturing the tail of the distribution, not giving enough probability to long distances.

The prediction based on 2003–2004 largely replicates the number of four-cycles in 2005 (overall the number of predicted four-cycles is a little lower than observed and as predicted using 2005, which is a consequence of, among other things, the estimate for 2003–2004 being lower than that for 2004–2005). The random walk, by comparison, predicts far too few four-cycles. Since the random walk already predicts too few four-cycles it almost manages to predict the number of C_MW.

By including the base-line model we have shown that the fit of our model is not an artefact of the restrictions stemming from looking at the evolution from one point in time to another – there is sufficiently much change to highlight the processes at work in the data.

7. Discussion

We introduced a model for bipartite evolution drawing on Snijders’ work on stochastic actor-oriented models, and showed how to apply this model for the study of interlocking directorates. Analysing data on firms traded at the Stockholm Stock Exchange between 1996 and 2005, we found that creating four-cycles seems desirable for corporate boards but that preserving them is not as important. We conclude that this is a sign of peer referral in the recruitment process, and that this is central to the evolution of the bi-partite network. However, the increase in female directors during the early 2000’s is not associated with any peer referral, suggesting that women where assigned to boards through other recruitment mechanisms. Lastly we showed by using time-series forecasting as cross-validation, that the fitted model managed to explain many features of the data that were not explicitly modelled.

In addition to the analysis conducted here there are some extensions that would be worthwhile pursuing. Although the strategic and instrumental interests of the corporations were not considered here it would be possible and useful to incorporate firm characteristics (e.g., Mizruchi and Stearns 1988) and business group affiliation (Smangs 2006), as well as board composition (e.g., Ruigrok et al. 2006) and additional director attributes. The literature also contains frequent mentioning of underlying networks and these could be taken into account to some extent by including director affiliation network (clubs and affiliations from e.g. who’s who). The question is whether the result would change considerably or whether these affiliations are already channelled through the social neighbourhoods and the peer referral process. A slightly different perspective would be to fully investigate the co-dependence of the board networks and other formal networks. It is a reasonable suggestion that there is co-dependence between the interlocking network and the ownership network (Bohman 2006). To analyse either one as evolving exogenously and independent of the other would be similar to when dyadic board covariates are employed. A more substantive interest would be to consider the joint co-evolution of the interlocking directorate network and the ownership network. Needless to say any of these further explorations would require extensive data collection in addition to the data that we had available for the current analysis.

For bipartite networks other than interlocking directorates model specifications would necessarily have to be redefined to reflect differences in boundaries, type of actions, etc. We believe that the methodology as laid out here goes some way towards giving directions as to how that could be made and that this opens for plenty of future applications, as do the opportunities to relax some of the simplifying assumptions made here. In addition to these extensions we could think of fitting a joint model for evolution using change point analysis techniques or likelihood-based model selection (Snijders et al., in press); treating changes in the population using birth and death processes for directors and boards.