Identifying Adverse Drug Events by Relational Learning

Abstract

The pharmaceutical industry, consumer protection groups, users of medications and government oversight agencies are all strongly interested in identifying adverse reactions to drugs. While a clinical trial of a drug may use only a thousand patients, once a drug is released on the market it may be taken by millions of patients. As a result, in many cases adverse drug events (ADEs) are observed in the broader population that were not identified during clinical trials. Therefore, there is a need for continued, post-marketing surveillance of drugs to identify previously-unanticipated ADEs. This paper casts this problem as a reverse machine learning task, related to relational subgroup discovery and provides an initial evaluation of this approach based on experiments with an actual EMR/EHR and known adverse drug events.

Introduction

Adverse drug events (ADEs) are estimated to account for 10-30% of hospital admissions, with costs in the United States alone between 30 and 150 billion dollars annually (Lazarou, Pomeranz, and Corey 1998), and with more than 180,000 life threatening or fatal ADEs annually, of which 50% could have been prevented (Gurwitz et al. 2003). Although the U.S. Food and Drug Administration (FDA) and its counterparts elsewhere have preapproval processes for drugs that are rigorous and involve controlled clinical trials, such processes cannot possibly uncover everything about a drug. While a clinical trial might use only a thousand patients, once a drug is released on the market it may be taken by millions of patients. As a result, additional information about possible risks of use is often gained after a drug is released on the market to a larger, more diverse population.

Figure 1 presents a sample database of electronic health records (EHR) and a few patient records. In this example of a modern EHR, available information includes phenotype data: such as gender, height, and weight, clinical data such as medical visits, lab tests, and prescriptions, and genotype data such as Single Nucleotide Polymorphisms (SNPs, or individual DNA positions where some variation can be expected). This paper proposes reverse machine learning as a post-marketing surveillance tool in order to predict and/or detect adverse reactions to drugs from EHR data. We apply this approach to actual EHR datasets, including datasets provided by the Observational Medical Outcomes Partnership (OMOP). This task poses several novel challenges to the Machine Learning (ML) community:

1. One cannot assume advance knowledge as to an ADE that a particular drug might cause. In some cases, we may suspect a specific ADE, such as increased risk of heart attack (myocardial infarction, or MI); in such a case, supervised learning can be employed with MI as the class variable. But if we do not know the ADE in advance, what class variable can we use? We propose using the drug itself as the class variable and claim that, while we already know who is taking the drug, examination of a model that accurately predicts drug use can give insight into ADEs. Because we seek to discover the ADE by building a model to “predict” drug use (who has been on the drug), rather than to predict the actual entity of interest (the ADE), we refer to this approach as reverse machine learning.

2. The data are multi-relational. Several objects such as doctors, patients, drugs, diseases, and labs are connected through relations such as visits, prescriptions, diagnoses, etc. If traditional ML techniques are to be employed, they require flattening the data into a single table. All known flattening techniques, such as computing a join or summary features result in either (1) changes in frequencies on which machine learning algorithms critically depend or (2) loss of information.

3. There are arbitrary numbers of patient visits, diagnoses and prescriptions for different patients, i.e., there is no fixed pattern in the diagnoses and prescriptions of the patients. It is incorrect to assume that there are fixed number of diagnoses or that only the last diagnosis is relevant. To predict ADEs for a drug, it is important to consider the other drugs prescribed for the patient, as well as past diagnoses, procedures, and laboratory results.

4. Since all the preceding events and their interactions are temporal, it is important to explicitly model time. For example, some drugs taken at the same time can lead to side-effects, while in other cases one drug taken after another can cause a side-effect. As we demonstrate in our experiments, it is important to capture such interactions to be able to make useful predictions.

5. We need to learn lessons from epidemiology, especially pharmacoepidemiology about how to construct cases and controls—positive and negative examples—as well as how to address confounders. Otherwise our methods will simply identify disease conditions associated with the drug for other reasons, such as drug indications or conditions correlated with use of the drug for other reasons.

Figure 1.

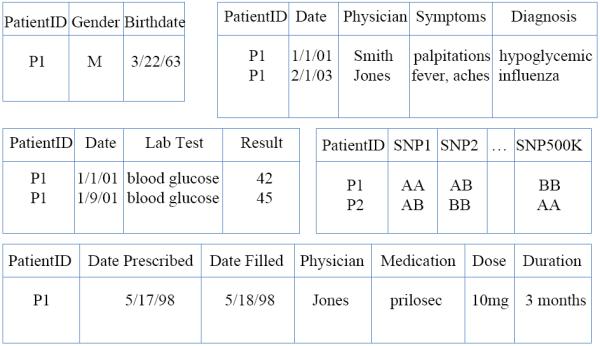
Sample structure of EHR

Contributions to Machine Learning

This paper presents a machine learning approach to studying an important, real-world, high-impact task—identifying ADEs—for which data sets are available through the Observational Medical Outcomes Partnership (http://www.omop.org). The paper shows how relational learning (Lavrac and Dzeroski 1994; De Raedt 2008) is especially well-suited to the task, because of the multi-relational nature of EHR data. In addition, this paper provides technical lessons for ML that should be applicable to a number of other domains as well. In this work, we follow the suggested structure of application papers in the Special Issue of the Machine Learning Journal on Applications (Kohavi and Provost 1998). We list these lessons here, discuss them as they arise in our presentation of the empirical analysis of our approach, and then review them again at the end.

1. In some ML applications, we may not have observations for the class variable. For example, we might hypothesize an unknown genetic factor in a disease or an unknown subtype of a disease. In such situations, we typically resort to unsupervised learning. The task of identifying previously unanticipated ADEs is such a situation – without an hypothesized ADE, how can we run a supervised learning algorithm to model it? Without knowing in advance that MI is an ADE for Cox2 inhibitors (Cox2ib), how can we provide supervision such that the algorithm will predict that MI risk is raised by these drugs? We show that the problem can be addressed by running supervised learning “in reverse,” to learn a model to predict who is on a Cox2ib. If we can identify some subgroup of Cox2ib patients based on the events occurring after they start Cox2ib, this can provide evidence that the subgroup might be sharing some common effects of Cox2ib. We anticipate this same approach can also be applied to other situations where the class variable of interest is not observed. We refer to this lesson as Reverse ML.

2. We introduce to ML some useful ideas from epidemiology, including treating each patient as his/her own control, by drawing as positive examples patients and their data after they begin use of a drug and as negative examples the same patients but before they begin use of the drug. Another idea we employ from epidemiology is to use a domain-specific scoring function that includes normalization based on other drugs and other conditions. We introduce to epidemiology the notion of learning rules to characterize ADEs, rather than simply scoring drug-condition pairs which require the ADE to correspond to an already-defined condition.

3. Finally, this paper reinforces the need for iteration between human and computer in order to obtain the models that provide the most insight for the task. In ADE identification, rules that are predictive of drug use can be taken as candidate ADEs, but these candidate ADEs must then be vetted by a human expert. If some of the rules are found to still capture other factors besides drug effects such as indications, then these rules should be discarded. We refer to this lesson as Iterative Interaction. Note that the prediction is reverse not only in terms of causality, but more importantly in terms of the label of interest.

Machine Learning for Predicting ADEs

Learning adverse events can be defined as follows:

Given

Patient data (from claims databases and/or EHRs) and a drug D

Do

Determine if evidence exists that associates D with some previously unanticipated adverse event

Note that no specific associated ADE has been hypothesized, and there is a need to identify the event to be predicted.

To our knowledge, ML has not been applied to this task before now. As mentioned above, our approach for this task is to use machine learning “in reverse.” We seek a model that can predict which patients are on drug D using the data after they start the drug (left-censored) and also censoring the indications of the drug. If a model can predict which patients are taking the drug, there must be some combination of clinical experiences more common among patients on the drug. In theory, this commonality should not consist of common causes for use of the drug, but common effects. The model can then be examined by experts to see if it might indicate a possible adverse event.

Formalizing Learning in Reverse

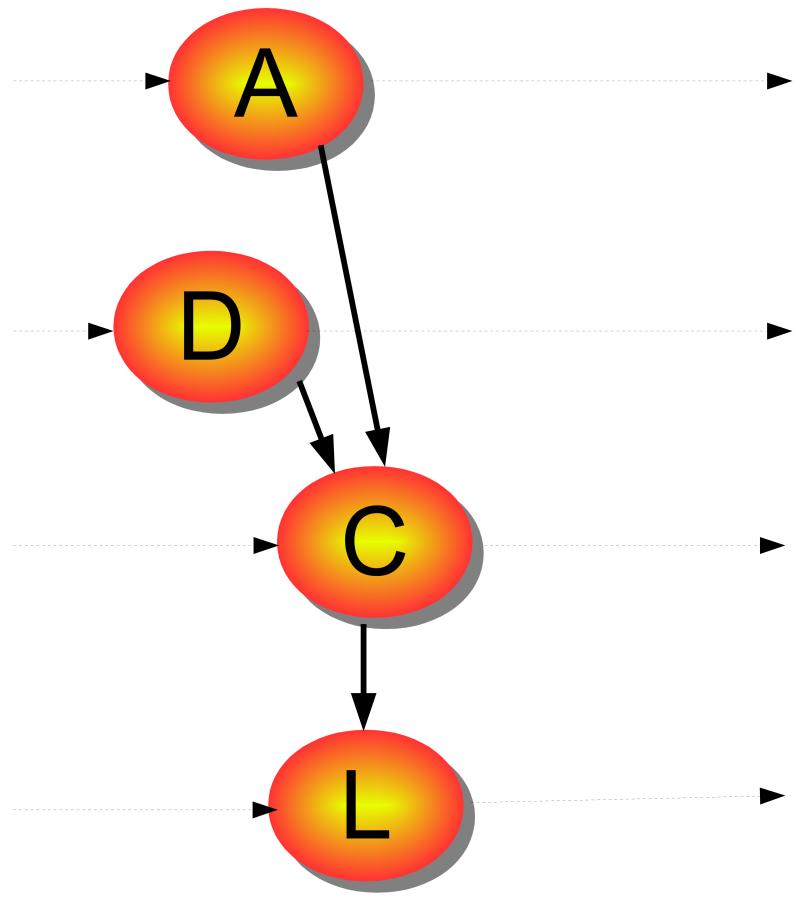
Given a (large) EHR and a drug, our task is to find a condition that is related to the drug. To better understand the complexity of the problem, consider the Markov model shown in Figure 2. The states are a set of partially observed variables ⟨A, C, L, D⟩, where A¹ are attributes of the patient, such as gender, age, family history, and genetic information; C are diagnoses; L are lab tests, and D are drugs prescribed. Given the dimensionality of the task, we chose to ignore latent variables (Saria, Koller, and Penn 2010) in this model.

Figure 2.

A temporal model capturing our problem; horizontal lines represent time.

We define an ADE to be an unexpected dependency between an observed variable in C and an observed variable in D, in the simplest case, or even some combination of variables in D. To our knowledge the present paper is the first to consider the more complex case of combinations, although we begin with the simpler case. Notice that vectors A, C, L, D have a large number of variables: our EHR includes over 10k reported conditions, and 4k to 5k different drugs. A standard approach to this problem is to assume two time-steps: events that happened before (step 0) and after taking a drug D_j (step 1). Techniques such as disproportionality analysis (Wilson, Thabane, and Holbrook 2004; Zorych et al. 2011) then search for a condition C_i such that its probability increases after taking drug D_j, i.e., $P(C_i^t\mid D_j^{t1})>P(C_i^{t^{\prime }}\mid D_j^{t1})$ s.t.t > t1 > t′, where $C_i^t$ denotes the condition C_i at time t. To do so, one must obtain estimators $\widehat{P}(C_i^t\mid D_j^{t1})$ and $\widehat{P}(C_i^{t^{\prime }}\mid D_j^{t1})$ and test against the null hypothesis. In practice, estimates can be confounded by other parameters. Typically, one will consider A and stratify at least over age and gender, and then weight the estimates. One can also go a step further and count time of exposure, as in observational screening. Focus on the temporal aspect is given by the univariate method (Newgard et al. 2004), where the condition C_i is considered the result of a non-homogeneous Poisson process with two rates, for during and after usage of drug D_j. A different method is to take into account confounding between different drugs. For example, a Bayesian logistic regression method (Caster et al. 2010) takes into account all drugs, plus gender and age information, to estimate the P (condition).

Essentially, these different methods search conditions $C_i^j$ such that their posterior probabilities of occurrence are greater than some threshold ( $P(C_i^j\mid {\mathrm{A}}^{1;t},{\mathrm{C}}^{1;t,}{\mathrm{L}}^{1;t},{\mathrm{D}}^{1;t})>\delta$ ) > δ), i.e., they search through the entire EHR for some conditions occurring with a non-trivial probability given the drug history. Given the size of the problem, they focus on different combinations of A, C, L, D. We use the ′ to refer to a (possibly empty) subset, say, D′ a subset of D. The previous approaches to the problem can be described as an enumeration of $P(C_i^j\mid {\mathrm{A}}^{\prime 1;t},{\mathrm{C}}^{\prime 1;t,}{\mathrm{L}}^{\prime 1;t},{\mathrm{D}}^{\prime 1;t})$ , given some fixed A′^1;t, C′^1;t, L′^1;t, D′^1;t.

In this work, we propose reverse learning. Instead of a direct search for C_i, we propose to enumerate over A′^1;t, C′^1;t, L′^1;t, D′^1;t and compute $P(D_j^k\mid {\mathrm{A}}^{\prime 1;t},{\mathrm{C}}^{\prime 1;t,}{\mathrm{L}}^{\prime 1;t},{\mathrm{D}}^{\prime 1;t})$ for some k as we know that if C_i is an ADE for D_j, then $C_i^l$ will be in a learned model for $D_j^k$ where l ≥ k. We thus reduce the problem of learning models for every condition C_i to the problem of finding out whether C_i is in a model for D_j. Thus, we can use standard learning technology to perform the search. Notice that our approach is akin to Bayesian inference, where we compute P(C|E) by estimating P(E|C). Indeed it reduces to this in the case where we just search over fixed subsets. On the other hand, the advantage is not in the Bayesian approach itself, as P(D_j|A′^1;t, C′^1;t, L′^1;t, D′^1;t) is not necessarily always easier to estimate than P (C_i|A′^1;t, C′^1;t, L′^1;t, D′^1;t): both are estimated from counts. The advantage is in transforming the learning process and making the problem supervised.

The strong relation between our work and Bayesian learning suggests a connection between reverse learning and abduction (Sato and Kameya 2002; Kakas and Flach 2009). Notice that in our setting the goal is not as much to learn a set of abducibles for an existing procedure, as to learn a new concept. Our problem is thus closer to the problem of predicate invention (Muggleton 1994; Richards and Mooney 1995; Davis et al. 2007; Muggleton et al. 2010). We believe that such insights will guide further progress in reverse learning.

Implementing Reverse Learning

To apply our reverse learning algorithm, we need to analyze in more detail:

1. EHR data are multi-relational and temporal, necessitating relational learning (De Raedt 2008) for this task.

2. The output of the learning process should be easy to interpret by the domain expert (Page and Srinivasan 2003).

3. Generally, only a few patients on a drug D will experience novel ADEs (ADEs not already found during clinical trials). The learned model need not, and indeed most often should not, correctly identify everyone on the drug, but rather merely a subgroup of those on the drug while not generating many false positives (individuals not on the drug). This argues that our reverse learning problem actually can be viewed as “subgroup discovery”(Wrobel 1997; Klosgen 2002; Zelezný and Lavrac 2006), in this case finding a subgroup of patients on drug D who share some subsequent clinical events.

This suggests using a relational rule-based classifier, since relational rules naturally induce subgroups on the data, are discriminant, and are often easy to understand. In our experiments, we use the ILP system, Aleph (Srinivasan 2004). In the remainder of the section, for concreteness, we present the discussion in terms of Aleph. Aleph learns rules in the form of Prolog clauses and scores rules by coverage (P – N), but this scoring function can be easily replaced by any user-defined scoring function.

Suppose we did not know that Cox2 inhibitors doubled the risk of MI, but we wondered if these drugs had any associated ADE. Our reverse ML approach can be seen as a case control study, where “cases”, or positive examples, are the patients on Cox2ibs and “controls” are the negative examples. Choosing controls is fundamental in obtaining good study quality (Rothman and Greenland 2008). We can use the patient him/herself as control. In this case the data on the patient prior to drug usage is the negative example. Alternatively, we can search for age- and gender-matched controls and use them as negative examples. In this case, for each positive example, a control is a patient of the same age and gender who is not on a Cox2ib. (Controls could be selected to be similar to the cases in other ways—age and gender are just the most common such features in clinical studies.) Because Cox2ibs double the risk of MI, we can expect our distribution of selected patients to appear as in Figure 3. For example, if we have say 200 positive (P) patients who suffer an MI, we expect about 100 negative (N) patients. The following rule would have a strong score of P – N = 100 and hence would be returned by Aleph unless some other rule scores even better.

$$cox2ib\left(Patient\right)\leftarrow mi\left(Patient\right)$$

This rule says that a patient was likely on a Cox2ib if they suffered an MI.

Figure 3.

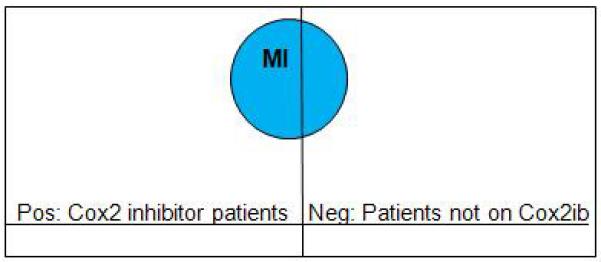
Distribution of people with risk of MI

Another advantage of the multi-relational approach, is that the body (precondition) of the rule does not have to be a single condition, but it can be a combination of conditions and lab results, possibly in a temporal order. Hence, ADEs that do not neatly correspond to an exact pre-existing diagnosis code can be discovered. Furthermore, the body of the rule can involve other drugs. So, ADEs caused by drug interactions can be captured. For example, it has recently been observed that patients on Plavix may have an increased risk of stroke (ordinarily prevented by Plavix) if they are also on Omeprazole. This can be represented by the following rule:

$$plavix\left(Patient\right)\leftarrow omeprazole\left(Patient\right)\wedge stroke\left(Patient\right)$$

Just because the rule is representable does not mean it will be learned. This depends on its support in the data, and the support of other rules that could score better, specifically as the support impacts the scoring function we employ.

In our experiments, we consider two cases. In the first case, we seek to associate drugs with specific conditions or candidate ADEs. In terms of relational learning, an association is represented by a rule, or definite clause, whose head is an atomic formula built from a predicate naming the drug and a variable standing for the patient, and whose tail is an atomic formula built from a predicate naming the condition and the same patient variable; this form is illustrated by the cox2ib and mi rule above. In this case our reverse learning approach is another way to carry out a standard association study, differing only in the scoring function we employ. In the second case, we do not assume a list of candidate ADEs or conditions; instead an ADE is represented by any conjunction of atomic formulas with predicates naming entities from the EMR such as conditions, observations (labs or vitals), or other drugs, or possibly predicates defined in a background theory such as before. In this case reverse learning extends beyond the standard association study methodology.

Experiments with OMOP Data and an EHR

Our first experiment is with a large real-world health insurance claims database available through OMOP. This was one of several databases available for evaluation of methods for ADE discovery (Ryan et al. 2010); OMOP evaluated methods by use of 10 known drug-ADE pairs such as Warfarin-bleeding and ACE inhibitor-Angioedema. Because OMOP had multiple different reasonable definitions for each ADE condition, this resulted in 35 ground-truth positive examples. All other pairs consisting of 1 of the 10 drugs with one of these 30 condition definitions were taken to be ground-truth negatives. This strong definition of negative examples may lead to somewhat pessimistic evaluation results, as evidence is accruing that some of these negative examples may actually be ADEs as well, such as a possible association between ACE inhibitors and renal damage. The methods were evaluated on a database with over 1.2 million subjects, and that includes 17M drug reports and 29M condition reports, for a total of 1300 drugs and over 10k conditions. The best approaches, with the best combinations of parameter settings achieved AUCROC around 0.8 (Madigan and Ryan 2011); this is quite high considering that many approaches did no better than chance (AUCROC of roughly 0.5).

As a first study, because all the other methods tested by OMOP ranked only drug-condition pairs, we limited Aleph to rules consisting of only a single condition in the body of the rule, that is, rules of the form of the following example:

$$warfarin\left(X\right)\leftarrow bleeding\left(X\right)$$

Aleph with its default scoring function and this constraint scored no better than chance. This was the case whether we chose positive and negative examples to be individuals on or not on the drug, or to be individuals (their diagnoses, drugs, labs, vitals, etc.) after or before drug use, respectively. We settled on choosing individuals as their own controls, and on a scoring function based on the posterior probability which has the following motivation.

We are interested in whether a drug d causes a condition, or ADE, c, but we are unable to carry out a controlled experiment to test causality. Following our reverse learning approach, we use each drug d as a reference, and Aleph computes for every condition c the counts of patients such that $P={\Sigma }_I\{I\mid t_{cI}>t_{dI}\}$ , and $N={\Sigma }_I\{I\mid t_{cI}\le t_{Id}\}$ . In this case, P/(P + N) is an estimator to the distribution Pr(t_c > t_d|c; d).

Note that one drug d might yield high probabilities for many conditions simply because it is frequently used by patients who are generally unhealthy or chronically ill; we can correct for this with a penalty term that incorporates all conditions, such as Pr(t_C > t_d|C, d): the number of patients in whom any condition C occurs later than d divided by the total number of patients who have any condition and the particular drug d. Also, a condition c might yield high values of Pr(t_c > t_d|c, d) for many different drugs d; again we can correct for this with an analogous penalty term Pr(t_C > t_d|C, d) over all conditions C. We can incorporate each penalty term by dividing the original metric by it, or by multiplying the original metric by one minus this penalty term. In practice both approaches work equally well for ranking drug-condition pairs. We can show that the above approach is equivalent to computing the point-wise mutual information (Mackay 2003) between ⟨d, c⟩ pairs.

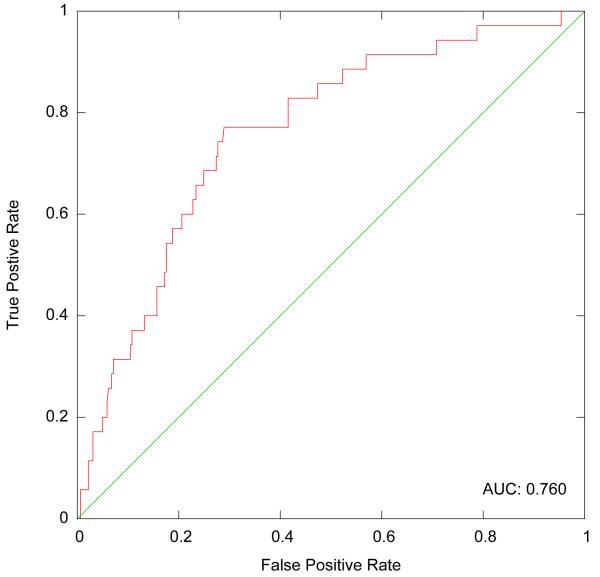
With this scoring function Aleph, achieves an AUCROC of 0.76, as shown in Figure 4. While this result is competitive without requiring parameter tuning, it nevertheless brings no improvement over other methods. The main benefit of using reverse machine learning with Aleph comes only with extending the possible lengths of the rule bodies. Our next experiment was to do so with the same data set. Runs of this type take substantially longer, varying from twenty minutes to almost seven hours depending on he drug. We no longer had ground truth against which to score these more complex rules, but we were able to evaluate their potential value, and especially their ability to pick up on drug-drug interactions. One of the top-scoring rules was:

$$warfarin\left(X\right)\leftarrow bleeding\left(X\right)\wedge antibiotics\left(X\right)$$

This rule represents a rediscovery that antibiotics elevate the risk of bleeding in patients on Warfarin, and the rule scores significantly better than a rule with bleeding alone.

Figure 4.

ROC Plot on OMOP data

Our second experiment is with a very different EHR. The Marshfield Clinic has one of the oldest internally developed EHRs (Cattails MD) in the US, with coded diagnoses dating back to the early 1960s. Cattails MD has over 13, 000 users throughout Central and Northern Wisconsin. Data collected for clinical care is transferred daily into the Marshfield Clinic Data Warehouse (CDW) where it is integrated. CDW is the source of data for this study. Programs were developed to select, de-identify by removing direct identifiers, and then transfer the data to a collaboration server. For this work, the specific CDW tables used were: ICD9 diagnoses, observations (lab results and others such as weight, blood pressure, and height), three sources of medication information and patient demographics (gender and birth date). Also associated with every entry was a date, so we provided Aleph background knowledge predicates to compare dates.

We ran on two drugs, Warfarin and Vioxx. For Warfarin the approach easily rediscovered the known ADE of bleeding, together with the common treatment for Warfarin-induced bleeding (Phytonadione, or Vitamin K1).

$$warfarin\left(X\right)\leftarrow bleeding(X,D1)\wedge phytonadione(X,D2)\wedge after(D1,D2)$$

Vioxx is a drug that was pulled from the market because it was found to double the risk of heart attack, or myocardial infarction (MI). We next tested to see whether Aleph would uncover this link with MI if the link were unknown. Vioxx belongs to a larger class of drugs called Cox2 inhibitors. The overall goal was to identify possible ADEs caused by Cox2ib. In our reverse ML approach, the specific goal of the Aleph run was to learn rules to accurately predict which patients had an indicated use of Cox2ib. These rules would then be vetted by a human expert to distinguish which were merely associated with indications of the drug (diseases or conditions for which the drug is prescribed) and which constituted possible ADEs (or other interesting associations, such as off-label uses for the drug). We first validate our methodology with a run in which only diagnoses are used and rules are kept as short as possible—one body literal (precondition) per rule. Myocardial infarction (MI) is a known adverse event of Cox2ib, and we wanted to test if the method would uncover MI automatically. In Table 1 we show the 10 most significant rules identified by Aleph for a single run. Note that the penultimate rule (highlighted) identifies the diagnosis of 410 (MI) as a possible ADE of Cox2. The fact that this ADE can be learned from data demonstrates that our method is capable of identifying important drug interactions and side-effects.

Table 1.

Aleph Rules Generated for Cox2 Inhibitor Use (Single Diagnosis)

In some cases, a drug may cause an ADE that does not neatly correspond to an existing diagnosis code (e.g., ICD9 code), or that only occurs in the presence of another drug or other preconditions. In such a case, simple 1-literal rules will not suffice to capture the ADE. We now report a run in which all of the background knowledge was used, including labs, vitals, demographics and other drugs. Table 2 shows the top ten most significant rules. The use of ILP yields interpretable rules. Fisher’s exact test indicated that many rules demonstrated a significant difference in identifying positive cases over chance. Aleph also provided summary statistics on model performance for identifying subjects on Cox2ibs, as shown below the Tables 1 and 2. If we assume that the probability of being on the Cox2ib is greater than 0.5 (the common threshold) then the model has an accuracy of 78% in predicting Cox2ib use. The sobering aspect of this result is that Aleph learns over a hundred rules, and while some are potential ADEs, most appear to simply describe combinations of features associated with indications for the drug. At present a clinician must then sort through this large set of rules in order to find any evidence for possible ADEs. Research is required to find ways to reduce the burden on the clinician, including automatically focusing the rule set toward possible ADEs and presenting the remaining rules in a manner most likely to ease human effort.

Table 2.

Aleph Rules Generated for Cox2 Inhibitor Use

Conclusion

This paper presents an initial study of machine learning for the discovery of unanticipated adverse drug events (ADEs). The key contributions and lessons learned for ML are:

• ML can be used “in reverse” when the real class value of interest—in this case, some unanticipated ADE—is not known at learning time. We show that this approach is able to successfully uncover ADEs.

• The paper demonstrates the importance of learning from years of epidemiology research in selecting our positive and negative examples for machine learning, as well as in setting our scoring function. We do not want to find patterns in the patients who get prescribed a particular drug, because we already know such patterns—they are the indications of the drug. Hence, it is important to control by using data about patients before the drug, as well as by total amounts of data on various conditions following various drugs.

• Another lesson is that despite our censoring, a high accuracy, or highly-accurate discovered subgroup, does not automatically mean we have uncovered one or more ADEs. Instead, all rules must be vetted by a human expert to determine if they are representative of an ADE or of some other phenomenon, such as that patients on arthritis medication such as Cox2ib also suffer from other correlated ailments. Once these associated conditions are also censored, learning ideally should be re-run in case ADEs were masked by other rules that scored better.

• Another lesson is that data are multi-relational, including longitudinal (temporal), and hence may be best analyzed by methods that can directly handle such data. It would be desirable to take into account time from drug exposure to events, but this is a challenging direction because different drugs can cause ADEs over different ranges of time. Some drugs may cause an ADE within hours after they are taken, whereas others may have permanent effects that only manifest themselves as an ADE years later.

Applications for Machine Learning in Active Surveillance

In addition to the task of ADE that we have presented, machine learning approaches could support many drug safety needs, including:

1. Identify and characterize temporal relationships between drugs and conditions across the population - Is there an association between exposure to rofecoxib and cardiovascular events such as MI? If so, what is the likely time-to-onset of the event, relative to exposure? Does the risk increase over time and vary by dose?

2. Identify drug-condition relationships within patient subpopulations - Among elderly, what are the observed effects of a particular medicine? Among patients with renal impairment, what is rate of adverse events?

3. Identify drug-drug interactions that produce harmful effects - Which concomitant drug combinations produce elevated risks, relative to exposure to individual products?

4. Identify risk factors and define patient subgroups with differential effects of a drug-related adverse event - Which patients are more likely to experience adverse events? Which patients less likely to experience adverse events?

5. Create models for predicting event onset - Which patients are likely to have experienced a MI, based on available information about diagnoses (AMI and other CV terms), diagnostic procedures (EKG), treatments (PCI), lab tests (troponin, CK-MB), and other observations.

Identifying previously-unanticipated ADEs, predicting who is most at risk for an ADE, and predicting safe and efficacious doses of drugs for particular patients all are important needs for society. With the recent advent of “paperless” medical record systems, the pieces are in place for machine learning to help meet these important needs.