On the use of low-frequency normal modes to enforce collective movements in refining macromolecular structural models

Abstract

As more and more structures of macromolecular complexes get solved in different conditions, it has become apparent that flexibility is an inherent part of their biological function. Normal mode analysis using simplified models of proteins such as the elastic network model has proved very effective in showing that many of the structural transitions derived from a survey of the Protein Data Bank can be explained by just a few of the lowest-frequency normal modes. In this work, normal modes are used to carry out medium- or low-resolution structural refinement, enforcing collective and large-amplitude movements that are beyond the reach of existing methods. Refinement is carried out in reciprocal space with respect to the normal mode amplitudes, by using standard conjugate-gradient minimization. Several tests on synthetic diffraction data whose mode concentration follows the one of real movements observed in the Protein Data Bank have shown that the radius of convergence is larger than the one of rigid-body refinement. Tests with experimental diffraction data for the same protein in different environments also led to refined structural models showing drastic reduction of the rms deviation with the target model. Because the structural transition is described by very few parameters, over-fitting of real experimental data is easily detected by using a cross-validation test. The method has also been applied to the refinement of atomic models into molecular envelopes and could readily be used to fit large macromolecular complex rearrangements into cryo-electron microscopy-reconstructed images as well as small-angle x-ray scattering-derived envelopes.

Understanding protein flexibility is a major challenge in structure–function relationship studies that structural molecular biology addresses routinely through both computational and experimental methods. Although normal modes analysis (NMA) has been known for years to be applicable to proteins to describe their movements (1–3), the method has recently enjoyed renewed interest because of the emergence of simplified models that proved easy to use and very effective in capturing the dynamics of proteins (4) but also because more and more structures of the same protein have been solved in different conformational states, providing more test cases. In many cases, it was observed that low-frequency normal modes are very good at explaining collective large-amplitude motions of proteins known in different conformational states (5). This result was shown for instance in a number of proteins undergoing induced fit upon ligand binding, particularly proteins existing in both a closed and an open form (6, 7). Other studies involve hemoglobin (8), but also large macromolecular complexes such as the ribosome (9) and even an entire viral particle (10).

In an extensive survey using a database of protein movements observed in protein structures deposited in the Protein Data Bank (PDB), Gerstein and colleagues (5) showed that, in most cases, a handful of the lowest-frequency modes deduced from NMA and a simplified representation of proteins is sufficient to explain the observed movements. This finding is based on the so-called elastic network model of proteins first described by Tirion (4) and then further developed independently by Hinsen (11) and Bahar and colleagues (12, 13). Normal modes calculated with this method are able to describe faithfully the B-factors (12, 14) in protein crystals. The obvious advantage of the elastic model is that NMA is very rapid and also that, thanks to the rotation–translation block (RTB) method recently developed by Sanejouand and colleagues (15), there is virtually no limit in the size of the macromolecular assembly one can study.

However, in most of these studies, NMA is essentially a “postmortem” analysis, in the sense that both structures have to be known before a tentative molecular explanation of the biologically relevant movement(s) can be offered. For the time being, the prediction of such movements from just one of the two structures remains a risky exercise.

In this article, we propose to use NMA to refine a starting structural model against experimental data such as medium- or low-resolution x-ray diffraction data, electron microscopy-reconstructed images of large macromolecular complexes or molecular envelopes derived from small-angle x-ray scattering data. We show that such a refinement procedure, using a very small number of parameters (the normal mode amplitudes of 10–20 lowest-frequency modes), has a very large radius of convergence. It is fast and robust, and its effectiveness can easily be monitored by the combination of the two reciprocal-space scores, R_work and R_free, that the community of crystallographers are routinely using during refinement of atomic models (16).

This method has numerous applications. The first application is in classical x-ray crystallography where it should supersede rigid body refinement, being just a generalization of the latter method. Indeed, it allows for global translations and rotations, but also for the movement of domains, without the obligation for the user to define subjective and somewhat arbitrary boundary regions of the different movable domains. In this respect, it is obvious that normal mode (NM) refinement could be used with benefit to get a better starting model after running a molecular replacement (MR) program, such as amore for instance (17), or even to identify the correct solution. Because the success of MR relies heavily on the ability to cope with large conformational changes in the original model, we expect NM refinement to be more useful than just rigid-body refinement, especially in the context of structural genomics.

A second application is to deform, in a plausible manner, an existing model into a known molecular envelope obtained either through electron microscopy (EM) image reconstruction techniques or small-angle x-ray scattering (SAXS) data. Indeed, EM and SAXS often offer the possibility of getting a low resolution image of the same macromolecular object in different conformational states, for instance after binding one or several ligands. In this case, NM refinement allows one to quickly gain detailed structural insight into the deformations induced upon ligand binding.

Due to the low number of parameters being refined, the method has a very favorable (no. of observations/no. of parameters) ratio that makes it very attractive when only a set of low-resolution experimental constraints is available.

Crystallographic refinement using NMA has been attempted before, especially in the pioneer papers of Kidera and Go (18) and Diamond (19). However, both works involved only the modeling of atomic (anharmonic) disorder through a better estimation of the Debye–Waller B-factors by using normal modes and made no attempt to refine the amplitudes of the normal modes to carry out positional refinement.

The application of deformations along normal modes eigen-vectors has been used before by Tirion et al. to fit fiber diffraction data on F-actin (20), but it seems that this work has remained isolated and was not pursued any further or applied to other cases. Also, the refinement was performed through the solution of the so-called normal equations and not with the conjugate-gradient method (21).

Materials and Methods

The Model. To calculate the normal modes, the protein structure is approximated by a three-dimensional elastic network, where each residue in the protein is reduced to one point (usually the C-alpha). Each point is linked to its neighbors in space by springs of the same strength C, which sets the energy scale (4–6, 11–15). There is only one parameter in this simple model, namely the cutoff R_c used to define neighbors in the structure. Here, we take R_c = 10 Å. The potential the protein is experiencing can be written as:

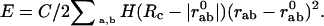[1]

Here, r_ab is the distance between two atoms a and b whereas is their distance in the reference state. C is a constant as in the original Tirion model (4). The sum is restricted through the Heaviside function H to “interacting” atoms, i.e., if < R_c. By construction, the reference conformation corresponds to the global minimum of the energy E.

It would be easy to modify the model so as to incorporate two elastic constants instead of just one, one for C-alpha atoms adjacent along the chain (whose distance should always be 3.8 Å) and the other (softer) for C-alpha atoms close in space. However, this precaution proved unnecessary in all of the cases described here.

The program used to calculate the normal modes, which are obtained by diagonalizing the matrix of the second derivatives of E (the so-called Hessian matrix), was written by Y.-H. Sanejouand. Typically, it takes 2–3 min of cpu on an XP1000 COMPAQ workstation for calculating the 100 lowest-frequency normal modes of a protein of ≈800 residues. If there are >1,000 residues in the protein, other strategies should be considered, such as the use of superresidues (15).

For each normal mode l, a set of eigenvectors 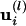is obtained for each eigenvalue; they represent the displacement at every residue i in the protein for this mode l. To describe a large-amplitude conformational change of a given protein, we need only the associated amplitudes c_l, which are the parameters to be adjusted against experimental data. The first six modes (associated with the same degenerate null eigenvalue) correspond to global translations and rotations. Refining against only these six modes will amount to a simple rigid body minimization.

Crystallographic Refinement. In reciprocal space, the structure factors F_calc(H) of the modified model with amplitudes c_l along the first Nmod (typically 20) lowest-frequency normal modes, read

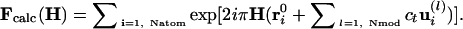[2]

To optimize the normal mode amplitudes against experimental data, the crystallographic residual R-factor is minimized by using a conjugate-gradient algorithm (21):

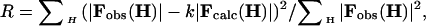[3]

where k is a scaling factor that may also incorporate a global B-factor.

Here, we used the routine zxcgr, which is also the minimizer used in cns (22); the derivatives ∂R/∂c_l needed by the minimizer were calculated analytically and checked numerically. Alternatively, one can minimize the score 1 - CC(|F_obs|,|F_calc|) where

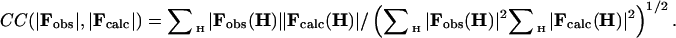[4]

In this case, the derivatives were calculated numerically only. In general, we prefer to use the latter criterion because it is scaling insensitive.

To monitor convergence and assess the effectiveness of the minimization process, ≈10% of the reflections were chosen randomly and subsequently left out of the refinement. The R-factor for this set of reflections was monitored and called R_free, following the definition of Brünger (16) whereas the R-factor corresponding to reflections being used in the minimization was called R_work (note that R_work and R_free have a correlation coefficient counterpart, CC-work and CC-free).

Synthetic Test Structure Factors. For the purpose of testing the program, a number of structures deformed along the normal modes directions were generated by randomly choosing the amplitudes of typically the 10–20 lowest-frequency normal modes, and the corresponding structure factors were generated in the appropriate space group.

We found it useful to monitor both the “mode concentration,” called I, as defined by Gerstein and colleagues (5): I = -Σ_l=1,Nmodc′_l ln c′_l/ln(Nmod) where c′_l = |c_l|/Σ_l=1,Nmod|c_l| are the normalized absolute values of the amplitudes.

At the end of the refinement, in test cases where the answer is known, the residual of the mode amplitudes R-mode = 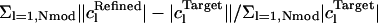was computed.

PDB Test Structure Factors. Two sets of structures were chosen for validating the refinement procedure, namely citrate synthase (PDB ID codes 5CSC and 6SCS) and the maltodextrin binding protein (PDB ID codes 1OMP and 1ANF) in both their open and closed forms. Experimental observed structure factors are available from the PDB for the closed forms. Their space groups are respectively P2₁2₁2₁ and P1. Citrate synthase is a dimer of ≈850 residues whereas the maltodextrin binding protein contains ≈370 residues. The overlap between the displacement vectors of the lowest-frequency normal mode and the difference vectors between the two forms is 0.83 and 0.86, respectively (6). The transition between the two forms is best described as a shear movement and a hinge-bending movement, respectively (5).

For MR tests, the open and closed forms of human polymerase β (1BPX and 1BPY) were used (335 residues). Structure factors of 1BPY were retrieved from the PDB (space group P2₁). The transition between the two forms is well described by NMA (7).

Envelope. For the envelope test, the envelope map was calculated from the coordinates of the full atomic model. For every point on a grid of size 100 Å × 100 Å × 100 Å and step size 5 Å the density was set to 1 if its distance to any protein atom was <1.8 Å. The density of all other points was set to 0. Structure factors of the envelope were obtained up to a 12-Å resolution by using the ccp4 package (23).

For the minimization, the phased correlation coefficient was used instead of the correlation coefficient on structure factors modulus only: in this case, Eq. 4 was replaced by

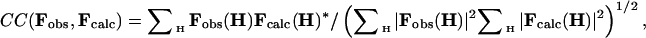[5]

where F_calc(H)^* is the complex conjugate of F_calc(H).

Although it is possible to refine C-alpha models directly, we found slightly better results in using the set of points on the grid inside the envelope as the protein elastic network. This procedure ensures that CC is exactly 1.00 for the correct envelope, allowing maximum contrast between a good and bad fit, and does not prevent an accurate calculation of the normal modes, as recently shown by Doruker and Jernigan (24).

Most fitting methods in reconstructed envelopes of macromolecules are based on correlation of model and experimental electron densities in real space (refs. 25 and 26, but see ref. 27 for a reciprocal space approach). Here, the refinement is carried out in reciprocal space with a model that has very few parameters.

Recovering the Final Model. After completion of the refinement process, the weighted sum of the normal mode displacement vectors, 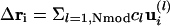was calculated and applied directly to the ith C-alpha coordinates of the initial model. For non-C-alpha atoms, interpolation was needed. We used a spherical averaging procedure with a weighting factor equal to the inverse of the mutual distance between the point of interest and points where the displacement vectors are known, i.e. the C-alphas, and located <10 Å away.

The resulting model was subjected to 250 cycles of Newton–Raphson energy minimization in cns (22), while harmonically restraining the positions of the C-alphas with a constant of 100 kcal/mol, so as to restore the stereochemistry of the protein chain. Superpositions of models and rms deviations (rmsd) were calculated with the McLachlan algorithm (28), as implemented in the program profit by A. C. R. Martin (www.bioinf.org.uk/software).

In the case of model refinement inside an envelope represented by a set of lattice points, the interpolation method of finding the displacement vectors for all of the atoms of the model was simply a tri-linear interpolation scheme (21).

Results

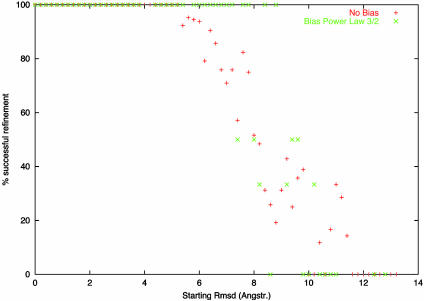
Refinement Against Synthetic Diffraction Data. The citrate synthase (ID code 5CSC) was considered first, and structure factors were calculated for deformed models of the protein obtained by varying amplitudes of the 10 lowest-frequency normal modes. These amplitudes were chosen randomly (positive or negative), and the calculated structure factors became the target structure factors against which the undistorted model was refined. The score being minimized was the correlation coefficient on the structure factors moduli (see Eq. 4). The absolute scale of the amplitudes was increased from one experiment to the other so that the total rmsd between the initial and the target model was increased. In Fig. 1, the percentage of correctly refined models is plotted as a function of the starting rmsd. There are ≈50 refined models in each bin of 0.5 Å of rmsd. In this way, we can evaluate the radius of convergence of the method, namely the initial rmsd of the model above which the refinements fail in >50% of the cases. The radius of convergence is around 8 Å, i.e. close to the resolution of the data used to do the refinement.

Fig. 1.

Refinement with respect to the 10 lowest-frequency normal mode amplitudes: proportion of models refined to better than 0.5 Å, as a function of the initial rmsd. To investigate the influence of normal mode concentration, a weighting scheme c_l/l^3/2 that most closely matches the observed one in the PDB was also used, showing a much sharper transition around 8 Å.

Gerstein and colleagues (5) developed the concept of mode concentration, based on the entropy of the absolute values of the normalized amplitudes needed to describe a particular conformational transition. They found that the mode concentration histogram is approximately a Gaussian curve with mean value 0.60 ± 0.10. By using this concentration quantity as a guide, we asked whether or not it is easier to refine a starting model if the amplitudes of the normal modes needed to describe the structural transition are “concentrated” in just a few modes or if they are “diluted”?

Different sets of 300–500 models were generated with random amplitudes of increasing maximum value, with different weighting schemes: 1, 1/l, 1/l^3/2 and 1/l², where l is the mode number. The corresponding average value for mode concentration is 0.9 ± 0.05, 0.8 ± 0.1, 0.65 ± 0.15, and 0.5 ± 0.2, respectively. In view of these figures, the distribution of amplitude concentrations observed with the 1/l^3/2 weighting scheme seems to follow closely the one observed in protein movements derived from the PDB. The refinement program is even better in this case, with a radius of convergence also equal to the resolution of the data, but with a much sharper transition (Fig. 1).

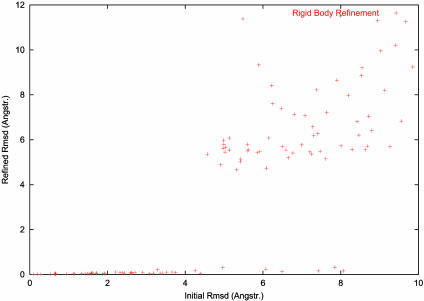
In a separate experiment, the ability of the program to function as a purely rigid-body minimizer was tested. The model was intentionally rotated and translated by various amounts and then refined against the structure factors of the unperturbed model. This time, the radius of convergence of the method was found to be around 5 Å (see Fig. 2).

Fig. 2.

Refinement with respect to the normal modes associated with null frequency: rigid-body refinement. The rmsd with the target model of the refined model is plotted as a function of the rmsd of the starting model. The refinement was carried out against calculated structure factors at a resolution of 8 Å. The minimized quantity is the score based on the correlation coefficient of structure factor moduli defined in Eq. 4, as in Fig. 1.

Finally, to test the dictum “when (degrees of) freedom are given, liberty is taken” (29), we generated a model with given amplitudes along the 10 lowest (non-zero) frequencies and refined the amplitudes of the 26 lowest normal modes, including the six rigid-body components. The program correctly finished the refinement with an amplitude of almost zero for the extra degrees of freedom that were allowed in this experiment, giving a final R-mode = 0.01. In practical applications (see below), we recommend trying to fit the data with 10–20 modes in at least two different situations, namely with or without the six rigid-body modes: the R-free criterion will determine which refined model is the best.

Refinement Against Real Diffraction Data. The open form of malto-dextrin binding protein (ID code 1ANF) was subjected to NM refinement against the experimental structure factors of its closed form (ID code 1OMP). Only C-alpha coordinates were selected, and data up to 4 Å resolution were used (≈5,500 reflections). Ten percent of the data were omitted from the refinement to monitor the R-free. The rmsd between 1ANF and 1OMP C-alpha coordinates is 3.8 Å. Only the five lowest-frequency modes were included. The results are presented in Table 1.

Table 1. Normal mode refinement against experimental diffraction data.

Starting model	Target model	Resolution (Nrefl)	Initial rmsd, Å	Final rmsd, Å	Initial CC (Free-CC)	Final CC (Free-CC)	Nmod	Natom (space group)
1ANF	1OMP	10 to 4 Å (5,500)	3.8	1.1	8.9 (9.7)	30.8 (28.1)	5	370 (1)
1OMP	1OMP	10 to 4 Å (5,500)	0.0	0.2	47.6 (49.6)	48.2 (49.4)	5	370 (1)
1ANF	1OMP	10 to 4 Å (5,500)	3.8	1.1	8.9 (9.7)	33.2 (28.5)	15	370 (1)
5CSC	5CSC	10 to 4 Å (7,860)	3.0	1.6	19.2 (15.2)	40.0 (39.7)	5	855 (19)
6CSC	6CSC	10 to 4 Å (7,860)	0.0	0.05	49.6 (48.2)	49.8 (48.5)	5	855 (19)

After conjugate-gradient minimization, the correlation coefficient on structure factors moduli increased from 8.9% (9.7%) to 30.8% (28.1%) where the values in parenthesis correspond to CC-free. The rmsd between the refined model and the target model was 1.14 Å, a considerable improvement from the initial value (3.8 Å). Displacement vectors corresponding to the five modes under consideration, weighted by their respective refined amplitudes, were applied to all atoms according to the procedure described above. The rmsd of the final full atomic model with the target model was 1.48 Å, after refinement with cns to regularize the stereochemistry. The cpu time of the whole process was <3–5 min even though no special effort was made to speed up the computation. The same experiment was repeated with the 15 lowest-frequency modes instead of only the lowest 5 ones, and the refinement converged to the same solution with a final correlation coefficient of 33% (28%).

As a control experiment, the correct model 1OMP was subjected to the same refinement protocol. The initial correlation coefficient was 47% (49%) and was not much modified after completion of the refinement, reaching 48% (49%). The amplitudes of the normal modes were very small, and the final model was only 0.18 Å away from the initial one, meaning that the correct model was not affected by the refinement, as expected (see Table 1).

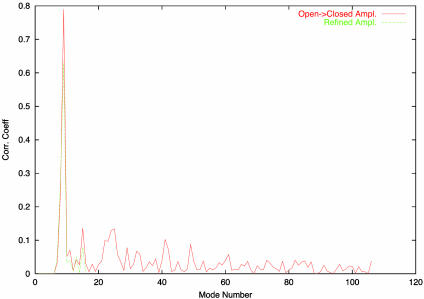
The same NM refinement was done on citrate synthase (5CSC and 6CSC). The rmsd between the open and closed forms is 3.0 Å. Refinement of the control model (6CSC) against its structure factor moduli gave a refined model only 0.05 Å away from the initial one and a stable correlation coefficient of 45%. Starting from the 5CSC, however, and refining against the 6CSC experimental structure factors, the correlation coefficient increased from 19% (15%) to 40% (39%) in <20 cycles (see Table 1). In this process, the third lowest-frequency normal mode received the largest amplitude, as it should (Fig. 3). The rmsd between the initial and refined model is 2.4 Å whereas the rmsd between the target and refined model is 1.6 Å.

Fig. 3.

Projection of the set of displacement vectors, for each low-frequency normal mode from 1 to 106, onto the set of difference vectors between the two forms the maltodextrin binding protein (PDB ID codes 1OMP and 1ANF). In green we show the refined amplitudes, using conjugate-gradient minimization in reciprocal space against real data.

In comparison, standard protocols of simulated annealing refinement in dihedral angle space (22) failed to reduce the R_free factor, in the same conditions, for both test cases: R_free remained stuck at 47.5% and 52.5% for 5CSC and 1ANF, respectively. The same was true for standard rigid body refinement using cns.

Because the model moves a lot during the refinement, it might seem advisable to update the normal mode calculation during the refinement. To test this idea, we stopped the refinement every time the model moved by >1.5 Å away from its original position and recalculated the normal modes before reentering the minimizer. The program converged to the same solution for the maltose binding protein and 15 normal modes (data not shown). The reason for this phenomenon is that the first 15 normal modes of the target model form a very good basis set for the 15 normal modes of the initial model, and vice versa.

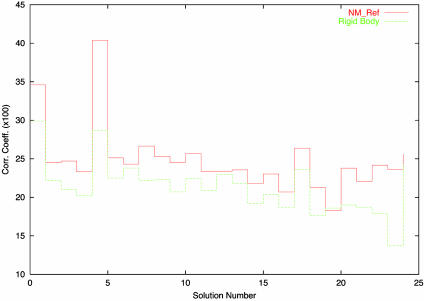
MR Test. The best solution of the translation function for each of the 25 first peaks of the rotation function implemented in amore (17) was refined by using data between 15 and 4 Å resolution either by standard rigid-body techniques or by allowing some extra degrees of freedom in the normal mode directions. In this case, the amplitudes of the 10 lowest-frequency normal modes were refined together with rigid body degrees of freedom. The correct solution, which is ranked second after rigid body refinement, is solution no. 5 in Fig. 4. NM refinement clearly identifies the correct solution by yielding a significantly higher correlation coefficient than the false positive solution no. 1. Clearly, this finding seems of real interest to enhance the range of application of molecular replacement in difficult cases.

Fig. 4.

Correlation coefficient of the top solution of the translation function for the 25 best solutions of the rotation function of the 1BPX model against 1BPY crystallographic data between 15 and 4.5 Å resolution. The true solution is solution 5; it is ranked first after NM refinement, but only second after rigid-body refinement.

Refinement Against Molecular Envelopes. Finally, an envelope was constructed for the closed form of citrate synthase (6CSC), and its structure factors were calculated in P1. The open form envelope was also calculated, and a set of grid points inside the envelope was used to compute normal modes, whose amplitudes were refined against the phased correlation coefficient of the closed form (see Eq. 5). The refinement was done at 12 Å resolution with ≈1,200 reflections. A definite improvement of the fit into the envelope of the closed form was observed with only five modes whereby the correlation coefficient increased from 87% to 93% in just a few seconds of cpu time (Fig. 5). The weighted displacement vectors of the grid points were then used to move the lattice points inside the envelope as well as the open form C-alpha coordinates, by using standard linear interpolation techniques (21). The rmsd of the resulting model with the target model was reduced from 3.0 to 1.8 Å. Adding more modes did not improve significantly the final correlation coefficient. The same refinement was attempted with maltodextrin binding protein (1OMP and 1ANF), resulting in the same kind of rmsd reduction, from 3.8 to 1.8 Å.

Fig. 5.

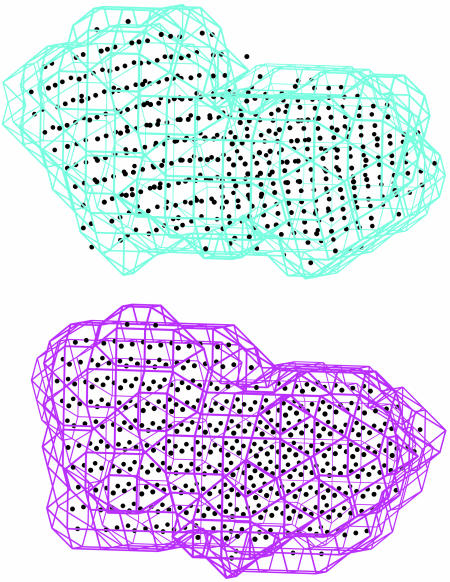
Envelope of the maltodextrin binding protein in the closed form together with the set of grid points inside the envelope (Lower). Envelope of the open form with the final set of refined points using the 10 lowest-frequency normal modes (Upper).

Discussion

Normal Modes and the Elastic Model. Impressive results were found for the refinement of structural models against medium- or low-resolution experimental data in reciprocal space, by using as sole parameters the amplitudes of a small set of low-frequency normal modes derived from a simple one-parameter elastic model of the protein. It is clear that normal mode refinement has a larger radius of convergence than classical rigid-body refinement (compare Figs. 1 and 2).

This finding might seem counterintuitive at first sight. In fact, it is just a consequence of the model described by Eq. 1 where low-frequency normal modes do enforce collective large-amplitude movements. Because the model contains very few parameters and is exactly accounted for in Eqs. 1 and 2, it is perhaps not so surprising that a relatively simple but robust conjugate-gradient minimizer can find the correct solution in very little cpu time.

The real question, therefore, is how well the model encoded in Eq. 1 describes biologically relevant large-amplitude movements of macromolecules. Loop movements and refolding events are likely to be poorly described by low-frequency normal modes.

Fortunately, it is possible here to invoke the systematic study of Gerstein and colleagues (5), who showed that a large proportion of protein movements documented in the PDB are indeed well described for the same protein in different environments (crystal packing, substrates, etc.), by just a few normal modes calculated by using the model represented by Eq. 1. This finding is complemented by a number of studies on specific systems (7–10). Also, a fortunate feature of the analysis in ref. 5 is that models with a mode concentration reproducing the one observed in the PDB refine even better than expected.

Limitations of the Model. At first sight, it might seem that a severe limitation of the method comes from the use of a highly partial model of the final structure, namely only the C-alpha coordinates are used both in the normal mode calculation and in the refinement process. However, several authors have argued convincingly that NM derived from C-alphas only (and not from the full atomic model) work well (5, 6). Two separate questions remain to be addressed.

First, the score for the correct model cannot be perfect if the model is partial, so the contrast between the correct answer and the starting model is not maximum, i.e., as large as it could be if the model were complete. However, we show here that this contrast is good enough to lead to a satisfactory refinement of NM amplitudes using real experimental data (see above).

Second, how can one generate the complete atomic model from the refined C-alpha coordinates? Here, we use techniques derived from homology modeling. There are actually at least two possibilities. The first one is to reconstruct all main chain atoms from C-alpha only, using fragments of the PDB database (30) as, for instance, implemented in the lego_auto_mc option in o (31) and then build side chains by using, e.g., mean-field techniques (32).

The second one is to interpolate displacement vectors at every atom position and then regularize the stereochemistry of the chain by using any molecular dynamics force field. We chose the second method with excellent results.

Fitting Models into Envelopes. It might seem that the approximation used here (to represent as a set of lattice points the model to be refined into a given experimental envelope) is a very gross one. However, it was shown recently that normal modes derived from such an approximation still correlate well with the ones derived, for instance, from a C-alpha model (24). Obviously there are other, and probably better, ways to represent the starting envelope, such as sets of points derived by more sophisticated neural-network techniques and Voronoi centroids (33–35). However, this method has the advantage of both simplicity and accuracy in the calculation of structure factors of the target envelope. It proved very easy to interpolate the field of displacement vectors back to the C-alpha coordinates, thus generating the atomic model in a matter of seconds of cpu time. Also, we find this visualization of the field of displacement vectors on a regular lattice very appealing for further analysis using graphics programs such as o (31).

For small-angle x-ray scattering data, the fitting could be done either in envelopes reconstructed from the experimental data (36, 37), or directly in reciprocal space, because the method presented here expresses the constraints in reciprocal space anyway. Further work is needed to assess which of the two methods is best.

Application to the MR Method. Highly partial models such as C-alphas-only models can be used and refined in MR techniques, as documented elsewhere (38, 39). The NM refinement program described here was successfully used to discriminate between alternative solutions of the MR problem, in a manner reminiscent of the Patterson-correlation-refinement method (40).

On a more general level, once the correct solution of MR has been identified, there is a definite need to start from the best possible model. This is because it is very difficult to get rid of errors in the initial model, which propagate during the refinement through phase combination. Even though phase combination methods have been improved (41, 42) and the R_free factor (16) allows for a better (safer) refinement process, there is still a definite advantage in refining early on (i.e., at low resolution) the molecular form of the model in the best possible way. NM refinement allows for such a possibility in cases where largeamplitude collective movements occur and where dihedral angle dynamics fail.

NM refinement is better than rigid-body refinement because there is no need for the user to define the movable domains, which are found by NMA. For shear movements as in citrate synthase, this feature is a definite improvement on existing methods because the movable domains are very hard to define by visual inspection. And, indeed, to explore large-amplitude rearrangements of the molecule, it seems natural to explore first the “most natural movements” of the protein, which are given by a linear combination of the lowest-frequency normal modes-associated directions.

Conclusion and Perspectives

In summary, we have shown here that refinement in reciprocal space at medium or low resolution with respect to NM amplitudes is very efficient, with a very large radius of convergence that goes beyond the capacities of pure rigid-body refinement and also of dihedral angle refinement. There is no danger of overfitting the data because the number of parameters is very small; in addition, the R_free indicator can be used to ensure that overfitting is not taking place. We checked in test cases that, when extra degrees of freedom are allowed, they refine correctly to almost zero amplitude. With real data, NM refinement proceeded correctly even though the model contains only one atom per residue.

Envelope refinement was made possible through the use of a lattice points approximation of the envelope, from which it was possible to interpolate the deformations of C-alpha coordinates of the molecule. Alternatively, C-alphas models can also be refined directly. We expect that the extraction of the normal modes amplitudes best fitting a molecular envelope change upon ligand binding should be extremely useful in the quickly expanding field of structural studies of large macromolecular biological complexes and/or molecular motors (43).