Characterization of the Zn(II) Binding Properties of the Human Wilms’ Tumor Suppressor Protein C-terminal Zinc Finger Peptide

Abstract

Zinc finger proteins that bind Zn(II) using a Cys₂His₂ coordination motif within a ββα protein fold are the most abundant DNA binding transcription factor domains in eukaryotic systems. These classic zinc fingers are typically unfolded in the apo state and spontaneously fold into their functional ββα folds upon incorporation of Zn(II). These metal-induced protein folding events obscure the free energy cost of protein folding by coupling the protein folding and metal-ion binding thermodynamics. Herein, we determine the formation constant of a Cys₂His₂/ββα zinc finger domain, the C-terminal finger of the Wilms’ tumor suppressor protein (WT1-4), for the purposes of determining its free energy cost of protein folding. Measurements of individual conditional dissociation constants, K_d values, at pH values from 5 to 9 were determined using fluorescence spectroscopy by direct or competition titration. Potentiometric titrations of apo-WT1-4 followed by NMR spectroscopy provided the intrinsic pK_a values of the Cys₂His₂ residues, and corresponding potentiometric titrations of Zn(II)–WT1-4 followed by fluorescence spectroscopy yielded the effective pK_a^eff values of the Cys₂His₂ ligands bound to Zn(II). The K_d, pK_a, and pK_a^eff values were combined in a minimal, complete equilibrium model to yield the pH-independent formation constant value for Zn(II)–WT1-4, K_f^ML value of 7.5 × 10¹² M^–1, with a limiting K_d value of 133 fM. This shows that Zn(II) binding to the Cys₂His₂ site in WT1-4 provides at least −17.6 kcal/mol in driving force to fold the protein scaffold. A comparison of the conditional dissociation constants of Zn(II)–WT1-4 to those from the model peptide Zn(II)–GGG–Cys₂His₂ over the pH range 5.0 to 9.0 and a comparison of their pH-independent K_f^ML values demonstrates that the free energy cost of protein folding in WT1-4 is less than +2.1 kcal/mol. These results validate our GGG model system for determining the cost of protein folding in natural zinc finger proteins and support the conclusion that the cost of protein folding in most zinc finger proteins is ≤+4.2 kcal/mol, a value that pales in comparison to the free energy contribution of Zn(II) binding, −17.6 kcal/mol.

Short abstract

The formation constant for a natural Cys₂His₂ ββα zinc finger peptide has been determined using a suite of equilibrium measurements. These data are compared to literature values for Zn(II)−Cys₂His₂ protein events to assess the free energy cost of protein folding in proteins with metal-induced protein folding events. The data lead to the conclusion that the free energy contribution of Zn(II) binding is far in excess of the minimal free energy cost of protein folding.

Introduction

Zinc finger transcription factors are one of the largest classes of eukaryotic proteins and are characteristic examples of structural Zn(II) proteins.¹ While classically recognized for their DNA/RNA binding ability,² zinc fingers are also involved in mediating protein–protein interactions³ and membrane association⁴ via lipid binding and may act as biological redox switches.⁵ One key structure–function relationship in zinc fingers is their metal-induced protein folding events.⁶ Zinc fingers are typically unstructured in the apo state, and they fold into their biologically active ββα fold upon Zn(II) incorporation. The Zn(II) is bound tightly, sub-nanomolar K_d values at physiological pH, using pseudotetrahedral Cys₂His₂, Cys₃His₁, or Cys₄ binding sites.^7,8 Because Zn(II) binding and protein folding are thermodynamically coupled in the metal-induced protein folding event, the precise free energy contribution of Zn(II) binding toward protein structure, assembly, and function is obscured by the underlying free energy cost of protein folding. Indeed, estimates of the free energy cost of protein folding in zinc fingers in the literature are as high as +16 kcal/mol.⁹

We have developed a method to separate the free energies of metal-ion binding and protein folding in zinc finger proteins.¹⁰ Our method is based on a designed 16 amino acid peptide scaffold, GGG, into which we individually incorporated each of the classic zinc finger metal-ion binding motifs, Cys₂His₂, Cys₃His₁, and Cys₄. The resulting three peptides, GGG–Cys₂His₂, GGG–Cys₃His₁, and GGG–Cys₄, each bind Zn(II) in a 1:1 stoichiometry in a pseudotetrahedral coordination motif with tight affinity, sub-nanomolar K_d values at physiological pH.^10,11 A suite of detailed equilibrium measurements over the pH range of 4–9 and a complete description of the metal–peptide binding equilibrium were used to measure their formation constant, K_f^ML (or β₁₁₀) values of 2.5 × 10¹³, 1.5 × 10¹⁵, and 5.6 × 10¹⁶ M^–1 for GGG–Cys₂His₂, GGG–Cys₃His₁, and GGG–Cys₄, respectively.⁹ The K_f^ML values of GGG–Cys₂His₂, GGG–Cys₃His₁, and GGG–Cys₄ indicate that cysteine thiolates are better ligands than histidine imidazoles^12,13 and that Zn(II) binding is favorable by 18.3, 20.7, and 22.8 kcal/mol, respectively. Additionally, these K_f^ML values are attenuated by the ligand pK_a values such that the K_d values at physiological pH are nearly identical, i.e. 1–5 pM. Because the GGG peptides have no secondary structure in the apo and holo forms, their free energy cost of protein folding is minimal and, correspondingly, their Zn(II) binding affinities, K_f^ML values, are tighter than natural zinc finger proteins with the same coordination motif. We¹⁰ and others¹⁴ have compared the free energies of Zn(II) binding to the GGG peptide with the free energy of Zn(II) binding to natural and synthetic zinc finger peptides and proteins with the same coordination motif to deduce the free energy cost of protein folding in the latter at specific pH values using conditional dissociation constant values. These data indicate that the free energy cost of protein folding in most zinc fingers is between 0–4 kcal/mol.¹⁰ However, a recent report by Sénèque and Latour,¹⁵ which reports substantially tighter Zn(II) affinity in the Consensus Peptide 1 series of designed zinc fingers and slow metal-ion exchange kinetics, indirectly questions this key result.

To date, our conclusions have been based on comparisons of conditional dissociation constants between our GGG model peptide and zinc fingers at individual pH values because of a lack of K_f^ML values for natural zinc fingers. Herein, we explore the effect of pH on the free energy cost of protein folding using a natural Cys₂His₂ zinc finger, the C-terminal finger of the Wilms’ tumor suppressor protein,¹⁶WT1-4. We have determined the formation constant for Zn(II)–WT1-4 to be 7.5 × 10¹² M^–1 using conditional dissociation constant measurements, EGTA and HEDTA competition constant measurements, and potentiometric titrations of the apo and holo forms. A comparison of the conditional dissociation constants of Zn(II)–WT1-4 to those from Zn(II)–GGG–Cys₂His₂ over the pH range 5.0 to 9.0 and a comparison of the pH-independent K_f^ML values demonstrate that the free energy cost of protein folding in both is identical within error. These results validate our model system and indicate that the pH effects on the cost of protein folding in peptides with an unstructured apo form are similar.

Experimental Section

Materials

Zinc(II) chloride, trifluoroacetic acid, ethanedithiol, 1-hydroxybenzotriazole, diethyl ether, acetic anhydride, diisopropylethylamine (DIEA), and piperidine were obtained from the Sigma-Aldrich Chemical Co. Aqueous stock solutions of Zn(II) were quantified by atomic absorption spectroscopy. Natural Fmoc-protected amino acids were obtained from Bachem. HBTU, O-(1H-benzotriazole-1-yl)-N,N,N′,N′-tetramethyluronium hexafluorophosphate, was purchased from Qbiogene. All other chemicals and solvents were reagent grade and used without further purification.

Chemical Synthesis of the Peptide

The 27 amino acid C-terminal zinc finger peptide of the Wilms tumor suppressor protein¹⁷ (WT1-4) was synthesized using sold-phase peptide synthesis.¹⁸ The crude peptide was purified to homogeneity with HPLC, and the identity of the purified peptide was confirmed with mass spectrometry. The sequence is given below with the zinc-binding residues highlighted in bold and the tryptophan residue in italics:

UV–vis Spectroscopy

UV–visible spectra were recorded on either a Varian Cary 100 or a Cary 300 spectrophotometer using anaerobic quartz cells of 1.0 cm path length. Peptide concentrations were determined spectrophotometrically using ε₂₈₀ of 5600 M^–1 cm^–1 for Trp.¹⁸

Circular Dichroism Spectropolarimetry

CD spectra were recorded on a Aviv Biomedical model 214 CD spectrometer using anaerobic quartz cells of 1.0 cm path length. Peptide concentrations were determined spectrophotometrically using ε₂₈₀ of 5600 M^–1 cm^–1 for Trp.¹⁸

Fluorescence Spectroscopy

Excitation and emission fluorescence spectra were recorded on a Cary Eclipse fluorimeter using anaerobic quartz cells of 1.0 cm path length. Excitation and emission slit widths of 5.0 and 2.5 nm, respectively, were employed. The excitation wavelength was 280 nm, and the fluorescence emission was collected from 300 to 450 nm. Peptide concentrations were between 1 and 25 μM, as determined spectrophotometrically using ε₂₈₀ = 5600 M^–1 cm^–1 for Trp.¹⁸

NMR Spectroscopy

A 1.2 mM sample of apo-WT1-4 in water was prepared in an anaerobic glovebox and placed into a NMR tube equipped with a J. Young valve for spectral measurement. The 600 μL sample of apo-WT1-4 contained 10 mM KCl, 0.1 mM DSS, and 10% D₂O. The pH was set using microliter aliquots of 0.1 M HNO₃ or 0.1 NaOH under strictly anaerobic conditions to prevent cysteine oxidation.

All 1D and 2D NMR spectra of the apo-WT1-4 peptide were collected on a Bruker DRX600 NMR spectrometer at 288 K. Water suppression in all 2D experiments was accomplished with the double gradient echo methods of Hwang and Shaka.¹⁹ The data were processed using NMRPipe²⁰ and extended using linear prediction and zero filling. The data were analyzed using NMRView.²¹ All proton resonances for apo-WT1-4 were assigned using the methods developed by Wüthrich.²² Intraresidue proton resonances were assigned using both short (15 ms) and long (80 ms) mixing time TOCSY experiments and a 225 ms mixing time NOESY experiment at 288 K using 640 t₁ increments at pH 6.0. The chemical shift values of the δ and ε protons of His²³, His²⁴, and His²⁷ as well as the β protons of Cys⁵ and Cys¹⁰ were then recorded from long mixing time (80 ms) TOCSY spectra collected at 17 different pH values under strictly anaerobic conditions.

X-ray Absorption Spectroscopy

Samples of Zn(II)–WT1-4 (∼1–2 mM) were prepared with 20% (v/v) glycerol and loaded in Lucite cuvettes with 6 μm polypropylene windows before rapid freezing in liquid nitrogen. X-ray absorption spectra were measured at the National Synchrotron Light Source (Brookhaven National Lab, Upton, NY), beamline X3B, with a Si(111) double crystal monochromator; harmonic rejection was accomplished using a Ni focusing mirror. Data collection and reduction were accomplished according to published procedures.²³ The data presented for Zn(II)–WT1-4 represent the average of the six scans.

Both raw and Fourier filtered EXAFS data were fit utilizing theoretical amplitude and phase functions calculated with FEFF ver. 8.00.²⁴ The Zn–N and Zn–S scale factors and the threshold energy, ΔE₀, were calibrated to the experimental spectra of the tetrakis-1-methylimidazole and tetraphenylthiolate complexes of Zn. These calibrated values (S_Zn–N = 0.78, S_Zn–S = 0.85, and DE₀ = −16 eV, with E₀ set to 9675 eV) were held fixed in subsequent fits to Zn(II)–WT1-4 data. First shell fits were then obtained for all reasonable coordination numbers while allowing the absorber–scatterer distance, R_as, and the Debye–Waller factor, σ_as², to vary. Fits to unfiltered EXAFS gave identical results. In no case did inclusion of a mixed first shell, with distinct Zn–N and Zn–O scattering contributions, result in either a significant improvement in fit residual or resolvable Zn–N/Zn–O distances. Multiple scattering contributions from coordinated histidines were fit using a set of combined multiple-scattering paths, according to published procedures.²⁵

Isothermal Titration Fluorimetry: Direct Metal-Ion Titrations

Aqueous stock solutions of Zn(II)Cl₂ unbuffered at pH 7.0 were added in microliter aliquots to freshly prepared WT1-4 peptide solutions in aqueous buffers under strictly anaerobic conditions in 1.0 cm cuvettes. Samples were allowed to equilibrate for at least 10 min (at least twice their measured equilibration time) before measurement of their fluorescence spectra. The conditional metal–ligand dissociation constants, conditional K_d values, were obtained from fitting a plot of the increase in tryptophan fluorescence at 355 nm against the [Zn(II)]/[WT1-4] ratio to the following 1:1 equilibrium binding model.

1

2

The equation used to fit the data is as follows

3

where Fl_meas, the measured fluorescence emission intensity, is a function of Fl₀, the fluorescence intensity of the WT1-4 peptide ligand prior to metal binding, Fl_lim, the limiting emission intensity of the Zn(II)–WT1-4 complex, M_T, the total concentration of metal added to peptide solution, L_T, the total concentration of the WT1-4 peptide, and K_d, the conditional dissociation constant.

Isothermal Titration Fluorimetry: EGTA and HEDTA Competition Titrations

For pH values above 6.0, conditional equilibrium dissociation constant determination for the Zn(II)–WT1-4 complex necessitated the use of EGTA (ethylene glycol tetraacetic acid) and HEDTA (N-(2-hydroxyethyl)ethylenediamine-N,N′,N′-triacetic acid) competition.^26,27 An unbuffered aqueous solution of Zn(II)Cl₂ at pH 7.0 was added in microliter aliquots to a buffered solution of 22.1 μM WT1-4 containing 5.0 equiv of competitor (EGTA or HEDTA) under strictly anaerobic conditions. The increase in fluorescence at 355 nm upon the addition of Zn(II) was fit to a competition equilibrium binding model based on eqs 4–8.

4

5

6

7

8

Where Fl_meas, the measured fluorescence emission intensity, is a function of Fl₀, the fluorescence of the WT1-4 peptide prior to metal binding, Fl_lim, the limiting fluorescence of the Zn(II)–WT1-4 complex, M_T, the total concentration of metal added to peptide solution, L_T, the total concentration of the WT1-4 ligand, EGTA_T, the total concentration of EGTA, and K_comp, the conditional competition constant.

The K_comp value, coupled with the conditional equilibrium dissociation constant value of Zn(II)–EGTA, K_d^{Zn(II)–EGTA}, given by eqs 9–11, gives the conditional equilibrium dissociation constant value for Zn(II)–WT1-4.

9

10

11

Where α_L is the mole fraction of fully deprotonated EGTA, K_f^{Zn(II)–EGTA} is the formation constant of fully deprotonated EGTA for Zn(II), a value of 10^13.1, and K_(1–4) are the stepwise proton dissociation constants of EGTA; K₁ = 1.0, K₂ = 3.1 × 10^–2, K₃ = 1.0 × 10^–2, and K₄ = 2.2 × 10^–3.²⁷

Potentiometric pH Titrations. Apo Peptide

The NMR spectra of WT1-4 support an unfolded apo state because very few interresidues NOEs were observed and chemical shift values of the Ha protons were very close to their random coil values.^22,28 The pK_a values for the metal-ion ligands in apo-WT1-4 were determined from fits of the graphs of chemical shift value versus pH for each of the Cys and His residues using the equation

12

where the measured proton chemical shift, δ_meas, is a function of protonated amino acid chemical shift, δ₀, the change in chemical shift due to deprotonation, Δδ, the solution pH value, and the acid dissociation constant of the amino acid pK_a. These four pK_a1–4 values establish the speciation of the apo-WT1-4, as shown in Scheme 1.

Scheme 1. Equilibrium Model for Zn(II)–WT1-4 Formation.

Potentiometric pH Titrations. Holo Peptide

Potentiometric pH titrations of Zn(II)–WT1-4 were performed manually using a 1.0 cm path length fluorescence cuvette fitted with a pH electrode under a stream of hydrated nitrogen gas. The pH of a 17 μM Zn(II)–WT1-4 sample in unbuffered water at pH 10 was adjusted by addition of microliter aliquots of 0.1 M HCl. Between each addition, the samples were allowed to equilibrate 3 min prior to measurement of their fluorescence emission spectra. The pH dependence of the fluorescence emission at 355 nm was fit to an equation for two separate protonation events, a cooperative two-proton event with an effective pK_a1,2^eff value and a cooperative two-proton event with an effective pK_a3,4^eff value that establishes the speciation of Zn(II)–WT1-4 given in Scheme 1.

13

Where the fluorescence emission at 355 nm measured at any pH, Fl_meas is a function of the initial fluorescence, and Fl₀, is the change in fluorescence due to the first and second protonation events, ΔFl₁ and ΔFl₂, respectively, the solution pH value, and the effective acid dissociation constants of the ligands bound to metal, pK_a1,2^eff and pK_a3,4^eff. For Zn(II)–WT1-4, the transition reflected by pK_a3,4^eff represented ∼65% of the total fluorescence intensity change, with the remainder represented by the pK_a1,2^eff-based transition.

pH Dependence of Conditional Dissociation Constants

Because of the expected proton dependence of the Zn(II)–WT1-4 conditional dissociation constants, K_d values were measured at varying pH values in order to determine the value of K_f^ML for each metal. The K_d values of Zn(II)–WT1-4 at each pH were determined as above using fluorescence spectroscopy. The resulting plots of −log K_d versus pH is fit to the following equilibrium binding expression for the pH-dependent formation of Zn(II)–WT1-4 from the WT1-4 peptide and {Zn(II)(H₂O)₆}²⁺ using the proton binding model in Scheme 1:

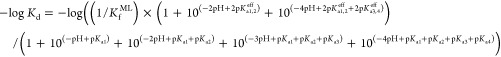14

The conditional dissociation constant at any pH, K_d, is a function of the pH-independent formation constant at high pH, K_f^ML, the effective acid dissociation constants of the metal-bound histidines, pK_a1,2^eff, and cysteines, pK_a3,4^eff, the acid dissociation constant values for the histidines, pK_a1 and pK_a2, and cysteines, pK_a3 and pK_a4, in the apo peptide, and the solution pH.

Results

Experimental Design

Zinc(II) plays a major role in biochemistry via its ability to stabilize protein structure.²⁹⁻³⁶ The largest class of metalloproteins encoded in the human genome,^37,38 the zinc finger proteins, are typically unstructured in the absence of Zn(II) and fold into their biologically active forms upon Zn(II) incorporation.⁶ Figure 1 shows the C-terminal zinc finger of the Wilms’ tumor suppressor protein (WT1-4), which folds into the classic zinc finger ββα fold upon binding Zn(II) to its Cys₂His₂ site.¹⁷ Indeed, zinc finger proteins are the prototypical examples of metal-induced protein folding events. Because the free energy of metal-ion binding is used to overcome the unfavorable free energy of protein folding, its actual value is obscured in typical measurements of metal–protein association/dissociation constants.

Figure 1.

(Left) Molecular model of the Zn(II)–WT1-4 complex rendered in PyMOL⁶⁸ and (Right) free energy diagram of zinc finger protein folding.

In zinc finger proteins (ZFPs) such as WT1-4, the free energy of Zn(II) binding to the Cys₂His₂ site is coupled to the free energy of protein folding.³⁹ Figure 1 shows that the apo-folded state is higher in energy than the apo-unfolded state of a typical zinc finger, with the difference equal to the free energy of apo-protein folding, ΔG_apo^folding. There is no direct method to measure the value of ΔG_apo^folding, which has been estimated to be between 0 and +16 kcal/mol.⁹ The free energy contribution of metal-ion binding, ΔG^ML, is the energy difference between the apo-folded and holo-folded states; the structure¹⁵ is shown for WT1-4 in Figure 1. ΔG^ML cannot typically be measured because of the uncertainty in the value of ΔG_apo^folding. The observed free energy contribution of metal-ion binding, ΔG^ML–obs, can be directly measured and is weaker than the free energy contribution of metal-ion binding, ΔG^ML, by the free energy cost of protein folding, ΔG_apo^folding, as follows:

15

We have developed a method to tease apart the free energy of metal-ion binding, ΔG^ML, from the free energy of protein folding, ΔG_apo^folding, in zinc finger proteins.¹⁰ Our method is based on a designed 16 amino acid peptide scaffold, GGG, into which we individually incorporated each of the classic zinc finger metal-ion binding motifs, Cys₂His₂, Cys₃His₁, and Cys₄. The resulting three peptides, GGG–Cys₂His₂, GGG–Cys₃His₁, and GGG–Cys₄, each bind Zn(II) in a 1:1 stoichiometry in a pseudotetrahedral coordination motif and have formation constant values of 2.5 × 10¹³, 1.5 × 10¹⁵, and 5.6 × 10¹⁶ M^–1, respectively, as determined using a suite of detailed equilibrium measurements over the pH range of 5–9.^10,11 Because the GGG peptides have no secondary structure in the apo and holo forms, their free energy cost of protein folding is minimal, ΔG_apo^folding = 0 kcal/mol, and their observed and actual free energy contributions of Zn(II) binding are equivalent. In natural ZFPs, the observed free energy of Zn(II) binding is weaker than the actual free energy because of the positive values of ΔG_apo^folding. Therefore, the difference in the actual free energy of Zn(II) binding to GGG to the observed free energy of Zn(II) binding to a ZFP can be used to reveal the cost of protein folding in the ZFP. We and others¹⁴ have compared the free energy of Zn(II) binding to the GGG peptide to natural and synthetic zinc finger peptides and proteins with the same coordination motif, derived from conditional dissociation constant values in the literature, to the free energy of Zn(II) binding to the GGG peptide with the same Zn(II) binding motif to determine the free energy cost of protein folding in the former.

16

These comparisons indicate that the free energy cost of protein folding in most zinc fingers is between 0 and +4 kcal/mol, and it does not appear to vary between the classic coordination motifs of Cys₂His₂, Cys₃His₁, and Cys₄ despite the fact that the K_f^ML values for each motif are distinct.

These conclusions are based on the comparison of the GGG peptide data to natural and synthetic zinc finger dissociation constants at single pH values. Although this has provided considerable insight into the free energy cost of protein folding in zinc fingers, the pH dependence of the conditional dissociation constant values is significant, and a comparison of the pH-independent formation constants, K_f^ML values, is more accurate because it removes effects resulting from changes in the His/Cys pK_a values. Because of the lack of K_f^ML values for natural zinc fingers, a comparison of K_f^ML values cannot be done at this time; in addition, any observed changes in conditional dissociation constants may reflect changes in K_f^ML values or the inherent His/Cys pK_a values. The closest comparison that can be done is for the Cys₃His₁ motif based on amino acids 34–51 of the HIV-1 nucleocapsid protein, (34–51)NCp7.^40,41 The reported K_f^ML value for (34–51)NCp7 is 2 × 10¹⁵ M^–1, which is identical, within error, to the 1.5 × 10¹⁵ M^–1 value reported for GGG–Cys₃His₁, indicating a similar cost of protein folding between these two peptides. However, any conclusions about zinc finger protein folding are somewhat speculative because the Zn knuckle fold of NCp7 is distinct from the classic zinc finger ββα fold. Additionally, the observed similarities in K_f^ML values between GGG and (34–51)NCp7 may reflect their size similarity, 16 versus 18 amino acids, or structural similarity, lack of helical/sheet structure in the two holo peptides.

Because the literature K_f^ML values for natural zinc fingers do not exist, we chose to evaluate a classic zinc finger with Cys₂His₂ coordination that adopts the classic ββα fold for this contribution. A single finger domain from the full-length four finger Wilms’ tumor suppressor protein (WT1) was selected, as the full-length protein required for kidney and genitourinary system development⁴²⁻⁴⁵ has been structurally characterized by both NMR and X-ray crystallography.¹⁷ The single C-terminal Cys₂His₂/ββα finger zinc finger, WT1-4, was selected for study because it is the only one with the intrinsic fluorescence probe tryptophan in its wild-type sequence. Herein, we present the first intrinsic pH-independent formation constant determination of a natural zinc finger protein with the classic ββα fold. The conditional dissociation constants and overall formation constant for Zn(II)–WT1-4 are determined using a suite of equilibrium methods that include the measurement of the pK_a and effective pK_a values of the His/Cys ligands, which provide a complete description of the metal–peptide binding equilibrium. These data are used to show that the cost of protein folding in WT1-4 over the pH range of 5–9 is minimal. These data validate our method for determining and evaluating the cost of protein folding across a wide pH range in a natural protein scaffold.

Fluorescence Spectroscopy

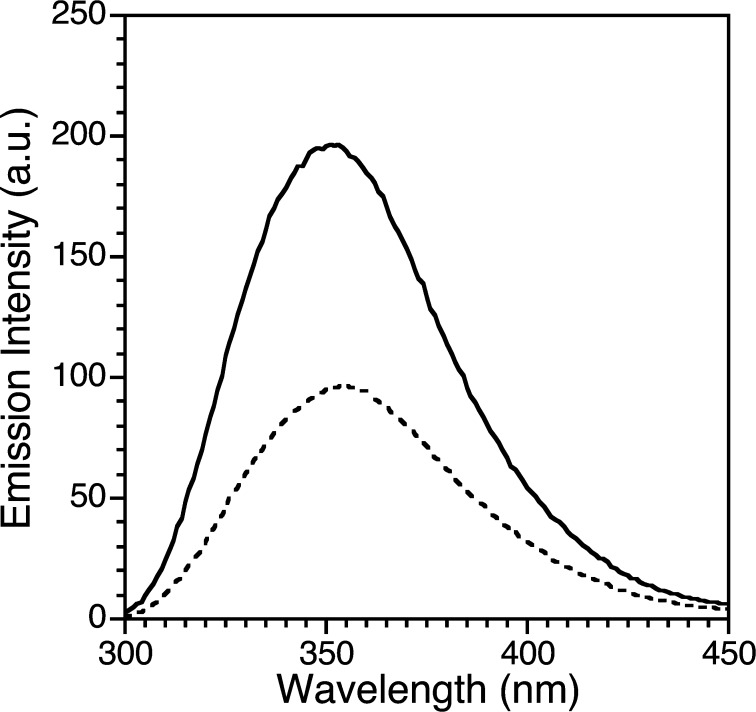
Figure 2 shows the steady-state fluorescence emission spectrum of WT1-4 and Zn(II)–WT1-4 at 22 μM concentration in aqueous buffer. The fluorescence emission maximum of Trp⁷ in apo-WT1-4 at 355 nm indicates that the indole ring is solvent-exposed.⁴⁶ Zn(II) binding to WT1-4 results in a slight blue-shift of the emission maximum to 350 nm, along with an increase in tryptophan fluorescence emission intensity, which is due, in part, to the elimination of the quenching mechanism of cysteine thiols.⁴⁷ The observed hypsochromic shift indicates that Trp⁷ in the metal-bound WT1-4 peptide is slightly protected from solvent, as evidenced in the NMR and X-ray structures of WT1, whereas Trp⁷ in apo-WT1-4 is more solvent-exposed.¹⁷ These data are consistent with an unfolded apo-WT1-4 that folds upon Zn(II) incorporation, and they provide a spectroscopic indicator of metal-ion binding.

Figure 2.

Steady-state fluorescence emission spectra of 22 μM apo-WT1-4 (dotted line) and 22 μM Zn(II)–WT1-4 (solid line) in pH 7.0 buffer (20 mM HEPES, 100 mM KCl). Each sample was excited through a 5 nm slit at 280 nm, the tryptophan λ_max value, and the fluorescence emission was collected through a 2.5 nm slit.

Isothermal Titration Fluorimetry

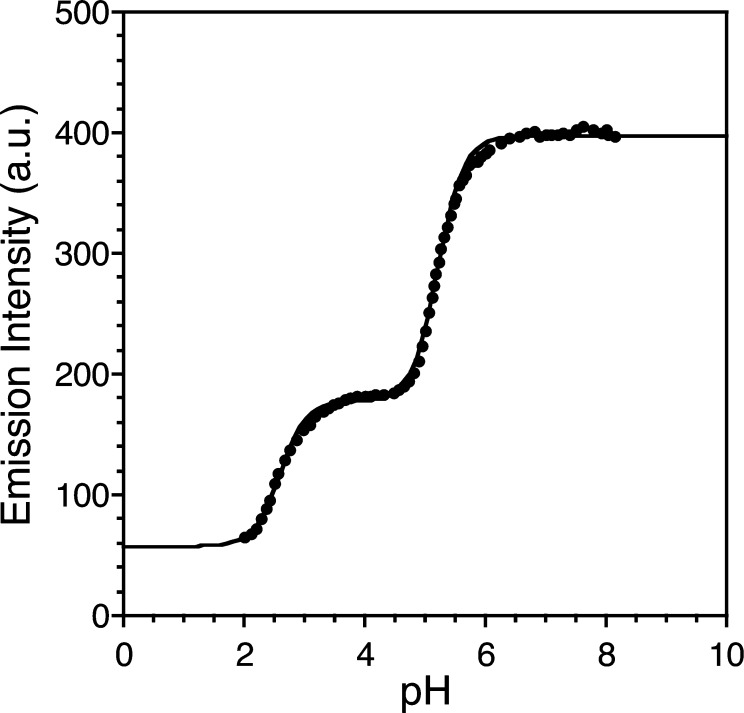
The intrinsic fluorescence of Trp⁷ was used to follow the incorporation of Zn(II) under a variety of solution pH conditions. The conditional dissociation constants for Zn(II)–WT1-4 were measured over the pH range of 5.0 to 9.0 using fluorescence spectroscopy because of the pH dependence on the K_d values resulting from proton release upon metal-ion binding to apo-WT1-4.

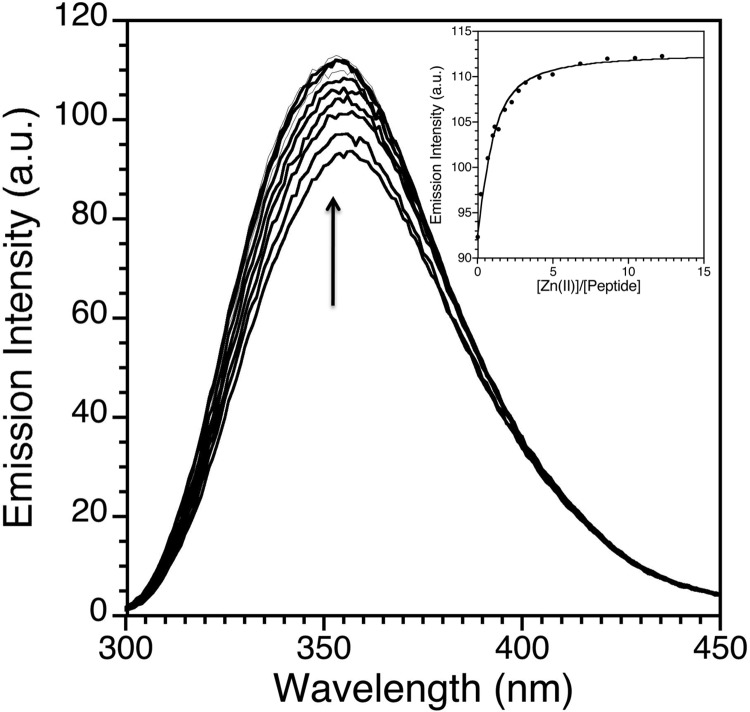
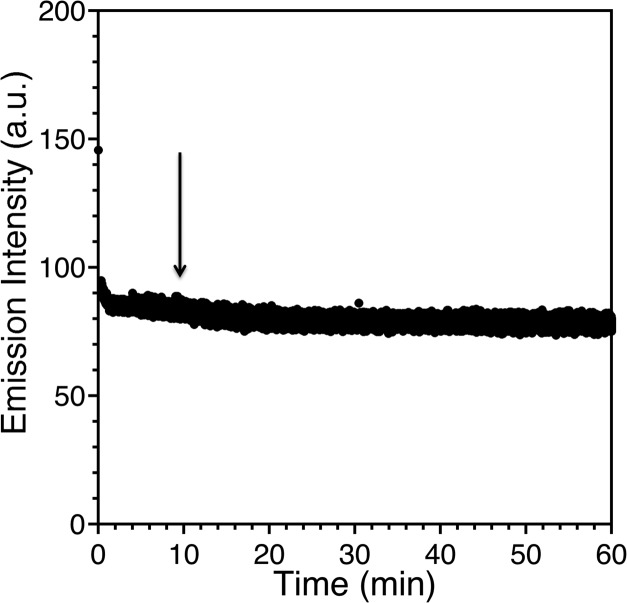
Figure 3 shows the direct titration of Zn(II) into 22 μM WT1-4 at pH 5.25 (20 mM MES, 100 mM KCl). The equilibrium binding isotherm shown in Figure 3 is fit to a 1:1 metal–peptide binding model, eq 3, and demonstrates a conditional dissociation constant value of 22 μM at pH 5.25. At pH values above 6.0, competition titrations with the chelators HEDTA and EGTA were performed to obtain accurate conditional dissociation constant values for Zn(II)–WT1-4. The formation constants for Zn(II)–HEDTA and Zn(II)–EGTA and their respective pK_a values were used to calculate their conditional dissociation constants between pH 6.0 and 9.0. Figure 4 shows a typical competition titration of Zn(II) into a buffered pH 9.0 (20 mM Tris, 100 mM KCl) solution containing 22 μM WT1-4 and 110 μM HEDTA. The equilibrium binding isotherm shown in Figure 4 is fit to a competition constant of 3.31. Because the K_d of Zn(II)–HEDTA is 2.01 × 10^–14 M at pH 9.0, the conditional dissociation constant of Zn(II)–WT1-4 is 6.6 × 10^–14 M at pH 9.0. Kinetic experiments were performed to ensure that samples had reached equilibrium. Figure 5 shows the change in fluorescence intensity as a function of time upon addition of 5 equiv of EDTA to 22 μM Zn(II)–WT1-4 in 20 mM MES, 100 mM KCl, at pH 6.65. The initial intensity, 145.67 au, decreases to 78.45 au in 15 min and remains constant for the following 45 min. Kinetic experiments from direct and competition titrations shows that all samples were equilibrated within 15 min, so measurements were taken 30 min after Zn(II) addition to ensure equilibration.

Figure 3.

Direct titration of Zn(II)Cl₂ in unbuffered aqueous solution at pH 7.0 into 22 μM WT1-4 buffered at pH 5.25 (20 mM HEPES, 100 mM KCl) followed by fluorescence spectroscopy. Spectra are shown for the addition of 0.00, 0.22, 0.67, 0.99, 1.81, 2.71, 4.07, 6.78, 8.59, and 12.20 equiv of Zn(II) added, with the others were omitted for clarity. The increase in emission intensity at 355 nm observed upon Zn(II) binding is fit in the inset to a Zn(II)–WT1-4 conditional dissociation constant, K_d, value of 9.9 μM at pH 25.

Figure 4.

Competition titration of Zn(II)Cl₂ in unbuffered aqueous solution at pH 7.0 into an aqueous solution containing 22 μM WT1-4 and 110 μM HEDTA buffered at pH 9.0 (20 mM Tris, 100 mM KCl) followed by fluorescence spectroscopy. Spectra are shown for the addition of 0.00, 0.90, 2.03, 2.94, and 4.29 equiv of Zn(II) added, with the others omitted for clarity. Under these conditions, a fit to the plot of fluorescence at 357 nm vs equivalents of Zn(II) added to peptide using eq 6 gives a competition constant value of 3.31 between WT1-4 and HEDTA. Because the K_d of Zn(II)–HEDTA at pH 9.0 is 20.1 fM, the resulting Zn(II)–WT1-4 dissociation constant at pH 9.0 is 66.5 fM.

Figure 5.

Kinetics of Zn(II) removal from 22 μM Zn(II)–WT1-4 by 100 μM EDTA buffered at pH 6.65 (20 mM MES, 100 mM KCl) followed by the decrease in fluorescence emission intensity at 355 nm. The fluorescence emission intensity drops from an initial value of 145.67 au to 78.45 au in 15 min. Under similar conditions, Sénèque and Latour¹⁵ measured an equilibration time for Zn(II)–CP1-CCHH of 1600 min.

Potentiometric pH Titrations

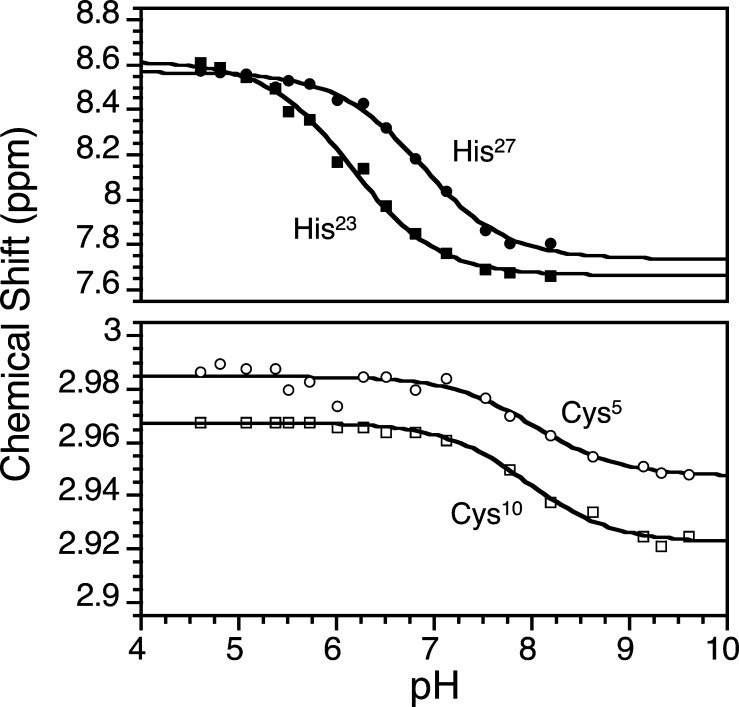
The pH-dependent chemical speciation of WT1-4 in the apo state and with Zn(II) bound were investigated using pH titrations followed by NMR and fluorescence spectroscopies, respectively. The chemical shifts of apo-WT1-4 were assigned at pH 6.0. The pH dependence of the Cys and His amino acid chemical shifts was determined using TOCSY. The pK_a values of the liganding residues were determined by measuring the proton chemical shifts of Cys⁵ (C^β-H), Cys¹⁰ (C^β-H), His²³ (C^ε1-H, C^δ2-H), and His²⁷ (C^ε1-H, C^δ2-H). Figure 6 shows that plots of proton chemical shift versus pH for each resonance were well-fit to single-proton pK_a values, eq 12. The data are fit to pK_a values of 8.0, 7.9, 6.2, and 6.9 for Cys⁵, Cys¹⁰, His²³, and His²⁷, respectively (Table 1). These values are close to the solution values for cysteine and histidine, as expected because of the unfolded nature of apo-WT1-4. In addition, these pK_a values establish the apo-peptide speciation in Scheme 1.

Figure 6.

pH titration of the Zn(II) binding residues in WT1-4 followed by NMR spectroscopy. The pH titration curves are fit to single-proton pK_a values of 8.0 (○, Cys⁵), 7.9 (□, Cys¹⁰), 6.2 (■, His²³), and 6.9 (●, His²⁷).

Table 1. pK_a and pK_a^eff Values of the Zn(II) Binding Residues in apo-WT1-4 and Zn(II)–WT1-4.

	pKa	pKaeff
Cys5	8.0	5.2
Cys10	7.9	5.2
His23	6.2	2.6
His27	6.9	2.6

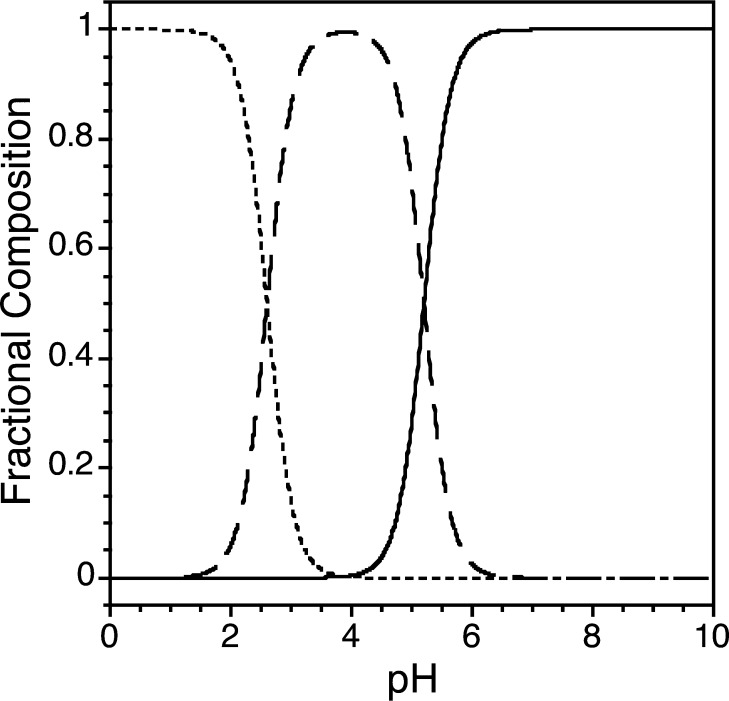
The pK_a^eff values of Zn(II)–WT1-4 were measured using potentiometric pH titrations followed by fluorescence spectroscopy to determine the appropriate Zn(II) proton competition equilbrium model. Figure 7 shows that titration of 0.1 M HCl into 15 μM Zn(II)–WT1-4 results in a decrease in tryptophan fluorescence. The pH titration of Zn(II)–WT1-4 is best fit to an equilibrium model involving two distinct two-proton protonation events, a coupled two-proton event at a pK_a1,2^eff value of 2.6 and a cooperative two-proton event at a pK_a3,4^eff value of 5.2, as shown in Scheme 1. These are assigned to the protonation of the Zn(II)-bound His residues (2.6) and Cys (5.2) residues (Table 1), as shown in eqs 17 and 18.

17

18

The measurement of these effective pK_a^eff values is critical to providing the correct Zn(II)–H⁺ competition model for the equilibrium presented in Scheme 1 and the speciation diagram for Zn(II)–WT1-4 shown in Figure 8. At pH values greater than 6.5, Zn(II)–WT1-4 is predominantly in the Cys₂His₂, cysteine thiolate/histidine imidazole, form, as shown in Figure 8. Between pH 3.0 and 5.0, the major species is Zn(II)–WT1-4 in the (CysH⁺)₂His₂, cysteine thiol/histidine imidazole, form. Lastly, below pH 2.5, the WT1-4 peptide exists mostly in the (CysH)₂His₂, cysteine thiol/histidine imidazolium, form without the metal bound.

Figure 7.

pH titration of 17 μM Zn(II)–WT1-4 followed by fluorescence spectroscopy. The decrease in tryptophan fluorescence emission intensity at 355 nm as the pH is lowered by addition of microliter aliquots of 0.1 N HCl is due to protonation/dissociation of the Zn(II) bound thiolate/imidazole ligands. The pH titration data is best fit to an equilibrium model involving two separate protonation events, a two-proton event with a pK_a1,2^eff value of 5.2 and a cooperative two-proton event with a pK_a3,4^eff value of 2.6.

Figure 8.

Speciation diagram of the Zn(II)–WT1-4 metal–ligand complex depicting the diimidazole–dithiolate zinc species (solid line), Zn(II)–WT1-4, the diimidiazole–dithiol zinc species (dashed line), Zn(II)–WT1-4–2H⁺, and the diimidazolium–dithiol species (dotted line), Zn(II)–WT1-4–4H⁺. The diagram was generated on the basis of the protonation behavior of the Zn(II)–WT1-4 complex in Figure 7.

Equilibrium Binding Model

The minimal complete equilibrium binding model for Zn(II)–WT1-4 established by the measured intrinsic pK_a and effective pK_a^eff values is presented in Scheme 1. The apo-state pK_a values indicated that each His and Cys ligand individually deprotonates, resulting in five species, generically LH₄ to L^4–, as expected. The slope of the potentiometric curves used to determine the holo-state pK_a^eff values show different behavior, namely, the cysteine thiols deprotonate as a pair, and the histidine imidazoliums deprotonate as a pair. The observed cooperativity in Cys and His deprotonation results in only three holo-state species, MLH₄²⁺, MLH₂, and ML^2–, where MLH₄²⁺ dissociates into M(II) and LH₄ under the conditions of our experiment. The speciation observed in the pK_a and pK_a^eff values is used to derive the expression for the pH dependence of the formation constant, eq 14. Therefore, measuring both the pK_a and pK_a^eff values is critical to establishing the speciation model used to determine the formation constant.

EXAFS Spectroscopy

To verify the coordination sphere of Zn(II) in complex with WT1-4 further, the k-edge EXAFS of the metal-bound peptide was examined. As can be seen in Figure 9 and Table 2, the data are best modeled with a Cys₂His₂ coordination sphere. As anticipated, the Zn–S scattering is substantially stronger than the Zn–N scattering, and modeling the first shell with all low-Z scatterers leads to a more than 2-fold higher fit residual than a model that contains only sulfur (compare the first two fits in Table 2). The mixed first shell of two nitrogen/oxygen and two sulfur donors gives a nearly 10-fold lower residual than the all nitrogen fit, which is also one-third that of the all-sulfur model. To better elucidate the best model for the coordination sphere, a percent improvement (P_i) versus composition plot (inset in Figure 9), where P_i is defined as P_i = (F_2S+2S – F_i)/(F_4S) × 100%, was constructed.⁴⁸ Comparison of the Zn(II)–WT1-4 fits (black line) with the curves previously reported for the Zn(II)–GGG–Cys₂His₂, Zn(II)–GGG–Cys₃His, and Zn(II)–GGG–Cys₄ peptides¹⁰ shows that the data for Zn(II)–WT1-4 is most consistent with that of the Zn(II)–GGG–Cys₂His₂ peptide. Multiple scattering fits, which have the lowest fit residual, further support Zn binding in a Cys₂His₂ site, with the outer shell scattering amplitude most consistent with the presence of two histidyl imidazoles in the primary coordination sphere of Zn(II). In addition, the distances of Zn–S (2.28 Å) and Zn–N (2.10 Å) in the 2S+2N (His) model are identical to the one that are previous reported for Zn(II)–GGG–Cys₂His₂ peptide¹⁰ and are similar to those observed in the NMR structure of full-length WT1 bound to DNA (Zn–S 2.29/2.30 Å and Zn–N 2.06/2.07 Å; PDB ID: 2JPG(17)). The corresponding distances in the X-ray structure of full-length WT1 bound to DNA (Zn–S 2.44/2.79 Å and Zn–N 2.21/2.29 Å; PDB ID: 2PRT(17)) are clearly different due to the moderate resolution of the X-ray structure, 3.15 Å. Overall, the EXAFS analysis indicates that the structure of the bound Zn(II) is the same in a single-finger (WT1-4) or the natural four-finger (WT1) construct.

Figure 9.

EXAFS Fourier transform for Zn(II)–WT1-4 (solid line) and best fit (open diamonds), modeled as a Cys₂His₂ coordination sphere. Inset: Percent improvement (P_i) vs composition plot for Zn(II)–WT1-4 (open symbols, black line) compared to those for characterized model peptides (gray lines, as labeled).

Table 2. EXAFS Curve Fitting Results for Zn(II)–WT1-4^a.

model	Zn–S	Zn–N	Zn–Hisb	Rfc	Ru
4 N		2.07 (6.2)		238	420
4 S	2.26 (11)			75	183
2 S + 2 S	2.19 (6.6), 2.32 (5.0)			61	176
2 S + 2 N	2.28 (2.8)	2.10 (2.4)		25	128
2 S + 2 N (2 His)	2.28 (2.8)	2.10 (2.6)	2.85 (18), 3.37 (2.2), 4.17 (10), 4.38 (16)	23	66

^aDistances (Å) and disorder parameters (in parentheses, σ² (10^–3 Ų)) shown derive from fits to filtered EXAFS data. Δk = 1.5–13.2 Å^–1; ΔR = 0.7–2.3 Å for first shell fits; ΔR = 0.1–4.5 Å for multiple scattering fits.

^bMultiple scattering paths represent combined scattering paths described in Experimental Section.

^cGoodness of fit (R_f for fits to filtered data; R_u for fits to unfiltered data) is defined as 1000 × (∑_i = 1^N{[Re(χ_icalc)]² + [Im(χ_icalc)]²})/(∑_i = 1{[Re(χ_iobs)]² + [Im(χ_iobs)]²}), where N is the number of data points.

Discussion

The formation constant for a natural Cys₂His₂/ββα zinc finger has been determined using a suite of equilibrium measurements and the minimal complete equilibrium model for metal–peptide binding. The data describe the metal-ion affinity and solution speciation of the C-terminal zinc finger domain in the Wilms’ tumor suppressor protein, WT1-4, which undergoes a metal-induced protein folding event. The data demonstrate the solution speciation of Zn(II)–WT1-4 and indicate a Zn(II)–WT1-4 formation constant of 7.5 × 10¹² M^–1, limiting K_d value of 133 fM, which demonstrates that Zn(II) binding provides up to 17.6 kcal/mol of free energy to facilitate protein folding and assembly. These results are identical within error to those of the GGG–Cys₂His₂ model peptide,¹⁰ formation constant of 2.5 × 10¹³ M^–1, limiting K_d value of 40 fM, 18.3 kcal/mol, indicating a similar, minimal cost of protein folding in the two peptides. The similarity between Zn(II)–WT1-4 and GGG–Cys₂His₂ extends to their pH-dependent conditional dissociation constants because of their similar Cys/His pK_a and metal-bound Cys/His effective pK_a values. The conditional K_d values of Zn(II)–WT1-4 are further compared with other zinc finger proteins from the literature at various pH values to reveal the cost of protein folding in the latter. These data indicate that most Cys₂His₂ zinc finger proteins possess a minimal cost of protein folding, <+5 kcal/mol, relative to the −17.6 kcal/mol contribution of Zn(II) binding. Furthermore, these results validate our use of the GGG–Cys₂His₂ model peptide to deduce the cost of protein folding in natural zinc finger proteins.

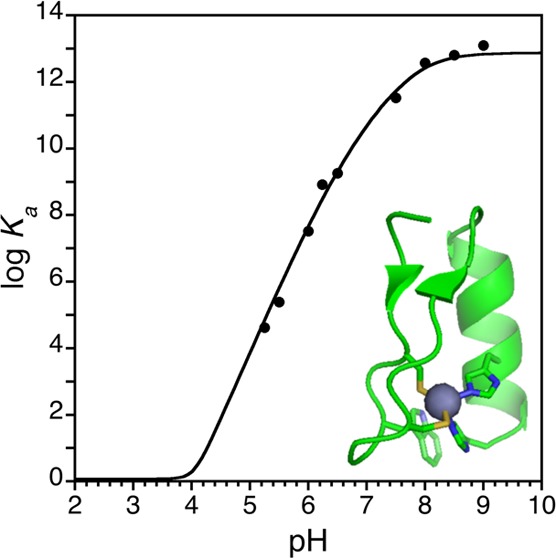
Scheme 1 shows the minimal complete equilibrium binding model for Zn(II)–WT1-4 that was established using the measured intrinsic pK_a and effective pK_a^eff values and used to determine formation constant value, K_f^ML (β₁₁₀), of 7.5 × 10¹² M^–1. Figure 10 shows the conditional association constants of Zn(II)–WT1-4 as a function of solution pH fit to eq 14 derived from our minimal complete equilibrium model. The plateau at basic pH yields the Zn(II)–WT1-4 formation constant value, which is attenuated at pH values below the apo-state pK_a values because of proton competition for Zn(II) binding. The slope of the attenuation approaches 4.0, as expected on the basis of the Cys₂His₂ coordination sphere, and plateaus below the pK_a^eff values to yield the Zn(II)–WT1-4-4H⁺ formation constant value, K_f^MLH₄ (β₁₁₄), of 1.2 M^–1. The complete model allows the independently measured conditional binding constants, pK_a and pK_a^eff values, to be validated against each other. Notably, the −18.3 kcal/mol free energy difference between the intrinsic pK_a and effective pK_a^eff values, derived from ΔΔG = 2.303RT(∑ pK_a^eff – ∑ pK_a), must be equivalent within error to the −17.7 kcal/mol free energy difference between the MLH₄²⁺ and ML^2– formation constant values, derived from ΔΔG = −2.303RT(log K_f^ML – log K_f^MLH₄) by definition. This provides a stringent check of the data and a validation of the equilbrium model used.

Figure 10.

pH dependence of the conditional dissociation constant of Zn(II) complexation by WT1-4, shown as a plot of the logarithm of the association constant vs solution pH. The equilibrium binding model employed to fit the data yields a pH-independent formation constant, K_f^ML value, of 7.5 × 10¹² M^–1, or a limiting dissociation constant of 133 fM, which corresponds to a reaction free energy of −17.6 kcal mol^–1.

The formation constant value, K_f^ML, of 7.5 × 10¹² M^–1 measured for Zn(II)–WT1-4 is identical within the 10-fold (1.4 kcal/mol) error to the 2.5 × 10¹³ M^–1 value previously reported for the Zn(II)–GGG–Cys₂His₂ model peptide.¹⁰ In each case, Zn(II) binding to the Cys₂His₂ site contributes about −18 kcal/mol toward protein folding and metalloprotein stability. Thus, the K_f^ML data show that the cost of protein folding in the two peptide scaffolds is identical within error, i.e. ΔG_apo^{folding–WT1-4} = ΔG_apo^{folding–GGG}. Because we assume that the value of ΔG_apo^{folding–GGG} is close to 0 kcal/mol as a result of the lack of secondary structure in its apo-unfolded and apo-folded states, the data indicate that the cost of protein folding in WT1-4 is also close to 0 kcal/mol. One might expect the longer sequence of WT1-4 compared to that of GGG to result in a larger cost of protein folding in the former because of the greater loss of conformational entropy. However, because the value of ΔG_apo^{folding–WT1-4} reflects the difference between the apo-unfolded and apo-folded states, it encompasses contributions from both favorable and unfavorable changes in enthalpy (ΔH) and entropy (ΔS). Restriction of the apo-unfolded ensemble to a structured apo-folded state involves an unfavorable ΔS term from the loss of conformational entropy and a favorable ΔH contribution from secondary structure formation and hydrophobic core packing in the apo-ββα structure. This situation where the unfavorable contributions to the folding free energy are offset by favorable terms appears to be the case also for the Cys₃His₁ site in the zinc knuckle fold of HIV-1 nucleocapsid protein (34–51)NCp7.^40,41 The K_f^ML values for (34–51)NCp7 and the corresponding GGG–Cys₃His₁ model peptide are 2 × 10¹⁵ and 1.5 × 10¹⁵ M^–1, respectively, indicating an identical cost of protein folding between these two peptides and thus a balance between the favorable and unfavorable free energy terms between the apo-unfolded state and the apo-folded state. Lastly, a comparison of the K_f^ML values from these Cys₂His₂ and Cys₃His₁ sites indicates that the Cys₃His₁site possesses higher affinity, bolstering our previous conclusion that cysteine thiolate of Cys is a better ligand than the imidazole of His for Zn(II).¹⁰

The similarity in the K_f^ML values of Zn(II)–WT1-4 and GGG–Cys₂His₂ does not necessarily indicate equivalent conditional dissociation constants, K_d values, because of the influence of the ligand pK_a values, both intrinsic and effective. In the case of Zn(II)–WT1-4 and GGG–Cys₂His₂, their Cys/His pK_a values are similar, likely due to the unfolded nature of their apo states. The similarity in the K_f^ML and the intrinsic Cys/His pK_a values between the two peptides results in similar Zn(II)–Cys/Zn(II)–His effective pK_a^eff values, by definition. The measured K_d values for Zn(II)–WT1-4 and GGG–Cys₂His₂ are all within 1.5 kcal/mol of each other at an individual pH values. These data indicate that the cost of protein folding in WT1-4 is also close to 0 kcal/mol over the pH range 5–9. A close inspection of the data shows a trend in that at pH values higher than 7.4, GGG–Cys₂His₂ has up to a 1.0 kcal/mol tighter affinity for Zn(II), whereas Zn(II)–WT1-4 has up to a 1.5 kcal/mol tighter affinity at pH values below 7.0 because of the ligand pK_a and pK_a^eff values. The His pK_a values (6.9/6.5 in GGG vs 6.9/6.2 in WT1-4) and the pK_a^eff values of the Zn(II)–Cys residues (5.6 vs 5.4) are nearly identical, but the Cys pK_a values (9.1/8.8 vs 8.0/7.9) and the pK_a^eff values of the Zn(II)–His residues (3.2/3.0 vs 2.7) show differences that lead to the observed changes in the K_d relative values. The Cys⁵ and Cys¹⁰ pK_a values of WT1-4 are likely lower (more acidic) than those in GGG because of the presence of local cationic amino acid side chains, Arg⁶, Lys¹², and Lys¹³. These pK_a and pK_a^eff changes reflect slight differences in proton management that effect the conditional dissociation constants while not affecting the overall formation constant K_f^ML values, which indicates the importance of determining both the pK_a and pK_a^eff values.

Table 3 shows the values of the free energy cost of protein folding, ΔG_apo^folding, derived for other Cys₂His₂ zinc proteins using either the GGG or WT1-4 data sets. The data show that the cost of protein folding values derived are slightly different depending on whether GGG or WT1-4K_d values are used. For example, the ΔG_apo^folding value of ZFY,⁴⁹ a Cys₂His₂/ββα zinc finger derived from the human Y-encoded protein, is either +2.3 or +3.7 kcal/mol at pH 6.5, based on the GGG or WT1-4 data, respectively. Similarly, the cost of folding the third Cys₂His₂/ββα zinc finger of the Wilms’ tumor suppressor protein, WT1-p,⁵⁰ is either −0.7 or +0.7 kcal/mol at pH 6.5 based on GGG or WT1-4 data, respectively. The values of ΔG_apo^folding change by up to 2.1 kcal/mol (Ros87⁵¹ at pH 6.8) depending on the model data set used and the solution pH, but this does not alter our prior conclusion that the cost of protein folding in most Cys₂His₂ zinc fingers is minimal, ≤ 4.2 kcal/mol. Our previous conclusion that the cost of protein folding in most zinc fingers regardless of zinc coordination motif is minimal is supported by Wilcox’s recent report¹⁴ on the physiological Zn(II) affinity of three natural proteins, Sp1-3, MyT1-2, and GR-2, which contain the canonical Cys₂His₂, Cys₃His₁, and Cys₄ coordination motifs, respectively.

Table 3. Cost of Protein Folding in Zn(II)–Cys₂His₂ Proteins.

protein	pH	protein Kd (log Ka)	protein ΔGML-obs (kcal/mol)	GGG ΔGML-obs (kcal/mol)	ΔGapofoldingGGG (kcal/mol)	WT1-4 ΔGML–obs (kcal/mol)	ΔGapofoldingWT-1 (kcal/mol)	protein fold
SUP3766	6.4	21 nM (7.7)	–10.5	–10.9	+0.4	–12.3	+1.8	ββα
WT1-p50	6.5	1.9 nM (8.7)	–11.9	–11.2	–0.7	–12.6	+0.7	ββα
ZFY49	6.5	300 nM (6.5)	–8.9	–11.2	+2.3	–12.6	+3.7	ββα
Ros8751	6.8	36 nM (7.4)	–10.2	–11.8	+1.6	–13.9	+3.7	βββαα
CP159	7.0	8.5 pM (11.1)	–15.1	–14.0	–1.1	–14.5	–0.6	ββα
CP115	7.0	1.2 fM (14.9)	–20.3	–14.0	–6.3	–14.5	–5.8	ββα
SP1-367	7.0	250 pM (9.6)	–13.1	–14.0	+1.0	–14.5	+1.4	ββα
SP1-314	7.4	20 nM (7.7)	–10.5	–16.3	+5.8	–15.6	+5.1	ββα
HCCHp56	7.4	54 nM (7.3)	–9.9	–16.3	+6.4	–15.6	+5.7	NDa
Ant-F57	7.5	12 nM (7.9)	–10.8	–16.5	+5.7	–15.7	+4.9	ββα

^aNot determined.

Several other lines of evidence in the literature support these conclusions. First, the successful redesign of a ββα zinc finger to be folded in the apo state did not increase the Zn(II) affinity dramatically, as would be expected if the cost of protein folding was large.^52,53 Second, molecular dynamics simulations of a zinc finger domain suggest that the ensemble of apo-unfolded states corresponds to the native state in an average sense.⁵⁴ Third, the successful computational redesign of a zinc finger into a stable ββα fold without the Zn(II) or the ligands indicates that hydrophobic interactions are sufficient to compensate for the loss of Zn(II) binding.⁵⁵ Lastly, the MI3 and MI4 proteins, natural homologues of the prokaryotic Cys₂His₂/βββαα zinc finger protein, Ros87, lack Zn(II) yet achieve the same functional fold.⁵⁶

There are at least two examples of zinc finger proteins with higher costs of protein folding in the literature, i.e. 6 kcal/mol. A +5.7 kcal/mol cost of protein folding, based on GGG and shown in Table 3, is observed for the artificial “antennafinger” Ant-F⁵⁷ at pH 7.5. The observed higher cost of protein folding is ascribed to the fact that Zn(II) binding induces a conformational change between two distinct folded states, a helical apo state and a less helical holo state. Thus, the free energy associated with Zn(II) binding is used to reorganize the helical apo-state conformation that is incommensurate with Zn(II) binding into the holo state. A similar situation may be observed for HCCHp,⁵⁸ a Cys₂His₂ zinc fingerlike peptide from the HIV-1 virion infectivity factor, which is reported to have some secondary structure in the apo state. The reported K_d value of 54 nM at pH 7.4 for HCCHp suggests a + 6.4 kcal/mol cost of protein folding compared to GGG–Cys₂His₂.

In our original report, we noted that Berg’s designed Cys₂His₂/ββα zinc finger Consensus Peptide 1^59,60 (CP1-CCHH) possessed a Zn(II) affinity that was slightly tighter than GGG and therefore had a ΔG_apo^folding value of −1.3 kcal/mol, which is within the error of the K_d measurements. However, a recent report by Sénèque and Latour¹⁵ reevaluates both the zinc affinity of CP1-CCHH and the metal-ion exchange kinetics, and their findings differ significantly from Berg’s initial reports. Sénèque and Latour report a K_f^ML (or β₁₁₀) value of 3.2 × 10¹⁷ M^–1 for Zn(II)–CP1-CCHH and a K_d value at pH 7.0 of 1.25 fM. These values are significantly tighter than our measured Zn(II)–GGG–Cys₂His₂ and Zn(II)–WT1-4 values, K_f^ML values of 2.5 × 10¹³ and 7.5 × 10¹² M^–1, and our measured K_d values at pH 7.0 of 56 and 22 pM, respectively, as well as Berg’s reported Zn(II)–CP1-CCHHK_d value at pH 7.0 of 5.7 pM.⁵⁵ Sénèque and Latour¹⁵ also observe slow metal-exchange kinetics (t_eq > 24 h at pH 6.65) when using EDTA competition titrations to determine the K_d values of Zn(II)–CP1-CCHH, whereas we observe rapid kinetics for metal-ion exchange between Zn(II)–WT1-4 and EDTA (t_eq < 15 min, at pH 6.65, shown in Figure 5) and Zn(II)–GGG–Cys₂His₂ (t_eq < 3 min, at pH 6.5), and Berg⁶¹ measured rapid displacement of Co(II) by Zn(II) in CP1-CCHH. Lastly, Sénèque and Latour observe that Cys to His substitutions yield Zn(II) affinities in the order CP1-CCCH > CP1-CCCC > CP1-CCHH, whereas we observe the trend GGG–Cys₄ > GGG–Cys₃His > GGG–Cys₂His₂. This difference likely reflects the geometic restrictions imposed by the folded holo state of the CP1 peptides.

The discrepancy between the CP1-CCHH data of Sénèque and Latour and Berg may reflect the different experimental conditions used to determine the Zn(II)–CP1-CCHHK_d values. Sénèque and Latour studied Zn(II) binding using UV (Zn–S charge transfer band, ε₂₂₀ = 8700 M^–1cm^–1) and CD (protein folding) spectroscopy in phosphate buffer in the presence of the water-soluble reductant TCEP, tris(2-carboxyethyl)phosphine, whereas Berg determined the Zn(II)–CP1-CCHHK_d values with UV–vis spectroscopy by Co(II) competition under strictly anaerobic conditions without TCEP or phosphate buffer. In our own experiments, we avoided the use of phosphate buffer and TCEP because of their interactions with Zn(II), Zn₃[PO₄]₂K_SP value of 9.0 × 10^–33 and TCEP K_f^ML of Zn(II)–TCEP is 813,⁶² and we utilized strictly anaerobic conditions. Our measured K_d values for Zn(II)–WT1-4 and Zn(II)–GGG⁹ agree with the thermodynamic studies of CP1-CCHH and its variants by Berg and others.^9,60,63,64 Additionally, we observe that the equilibria of metal-ion binding and metal-ion removal by EDTA are established within 15 min for both WT1-4 and GGG, consistent with the metal-ion substitution kinetics of CP1-CCHH. Furthermore, our results agree with other thermodynamic studies on natural zinc fingers in the literature, as shown in Table 3.

While resolution of the differences observed in Zn(II)–CP1-CCHHK_d values is beyond the scope of this report, the reported K_f^ML (or β₁₁₀) value may have a significant impact on our method for deducing the cost of protein folding in zinc finger peptides and proteins. Sénèque and Latour¹⁵ report that CP1-CCHH binds Zn(II) 13 900-fold, or 5.6 kcal/mol, tighter than GGG–Cys₂His₂ and 42 700-fold, or 6.3 kcal/mol, tighter than WT1-4 based on the K_f^ML values. This finding suggests that it costs +5.6 kcal/mol to fold GGG–Cys₂His₂ and therefore +5.6 kcal/mol should be added to all of the ΔG_apo^folding values derived from GGG–Cys₂His₂. In order to validate our approach to determining the cost of protein folding in Zn(II) proteins further, we are currently determining the K_f^ML value of human transcription factor IIB (TFIIB), a Cys₃His₁ zinc ribbon protein that is folded into the same structure in both the apo and holo states, as shown by NMR spectroscopy.⁶⁵ Thus, we expect the measured K_f^ML value to reflect the zero cost of protein folding in TFIIB.

Conclusions

In the present work, we have evaluated the formation constant for a natural zinc finger protein domain, the C-terminal zinc finger of Wilms’ tumor suppressor, in an effort to validate our protein folding free energy calculation methodology with a natural zinc finger domain over a wide pH range. A comparison of the formation constants and the condition dissociation constants at physiological pH demonstrate that the Cys₂His₂ zinc-binding sites in WT1-4 and GGG have comparable affinities, within the 1.4 kcal/mol (10-fold) error of the measurements. This fact leads to the conclusion that the free energy cost of protein folding in the natural zinc finger, WT1-4, and the simple peptide, GGG, is comparable. Furthermore, given the lack of secondary structure in GGG, we assert that the free energy cost of protein folding in GGG is close to 0 kcal/mol. It then follows that the cost of protein folding in WT1-4 is also close to 0 kcal/mol.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States