Figure 6. Computational simulations of intra-Golgi transport of albumin by diffusion via intercisternal tubules.
(A) The Golgi stack was modeled as a system of six circular cisternae connected in series by five (one per pair of cisternae) vertical cylindrical tubules. (B) The same stack drawn in a ‘distended’ disposition. The size of the cisternae was set to 1.5 μm diameter and 30 nm thickness, and the diameter and length of the tubules to 30 nm and 100 nm, respectively. The simulations started with the first cisterna (cis) filled with albumin (black shading) and all of the others empty (no shading). Albumin was then allowed to diffuse through the connections until it asymptotically reached equilibrium (gray shading in all cisternae). The variations with time in the albumin concentrations in the other cisternae were calculated for the center of the cisternae (see below). For wider tubule diameters of 60 nm and 120 nm, the 90% threshold of equilibrium was reached after 7.8 s and 6.8 s compared to 14.9 s for the 30 nm diameter. For shorter and longer tubules of 30 nm diameter with 50 nm and 150 nm lengths, the 90% threshold of equilibrium was reached after 11.4 s and 19.1 s. When assuming a system composed only of four circular cisternae, the 90% threshold of equilibrium in the fourth cisternae was reached after 3.4 s (60 nm diameter, 100 nm length) and 3.0 s (120 nm diameter, 100 nm length) compared to 6.4 s for the 30 nm diameter tubules. For shorter and longer tubules of 30 nm diameter with 50 nm and 150 nm lengths, the 90% thresholds of equilibrium were reached after 5.0 s and 8.4 s. (C and D) Time-courses of the equilibration process with different Golgi configurations and with stable or transient (flickering) intercisternal tubular connections. (C) One stack of six cisternae connected by one stable tubule per pair of adjacent cisternae (five connections in all), or by one transient tubule per pair of adjacent cisternae. The tubules were set to be open for 50% of their time, with equal average open and closed times as indicated. In these simulations, the individual tubules opened and closed randomly. (D) Simulation of diffusion based albumin transport in Golgi ribbons of one (blue), three (red), or five (yellow) stacks (each with 6 cisternae). The ribbons were completely connected horizontally by tubules joining adjacent cisternae. The total number of connections was five in all cases. For instance, the three-stack ribbon had one or two connections per stack. Nevertheless, complete equilibration was reached in less than 60 s. (E) Possible diffusion route of a soluble cargo through the Golgi ribbon with three stacks where the longitudinal tubules connecting the isolated stacks compensate for the vertical connectivity gaps. (F) Diffusion of a soluble cargo across a stack through transient intercisternal tubules.
Figure 6—figure supplement 1. Computational simulation of the intra-Golgi equilibration of albumin argues against the classic vesicular transport model.
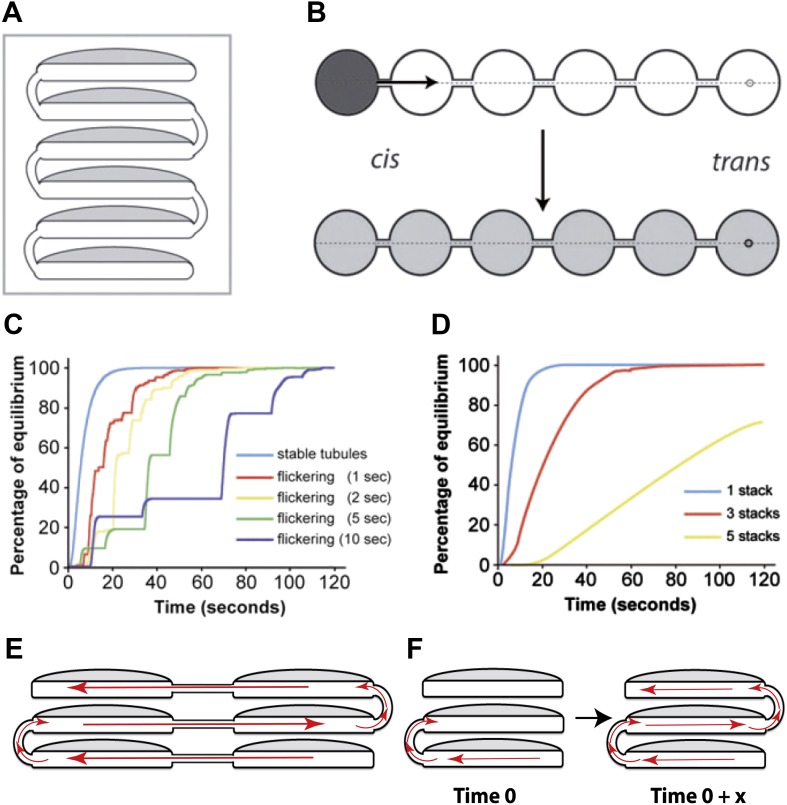
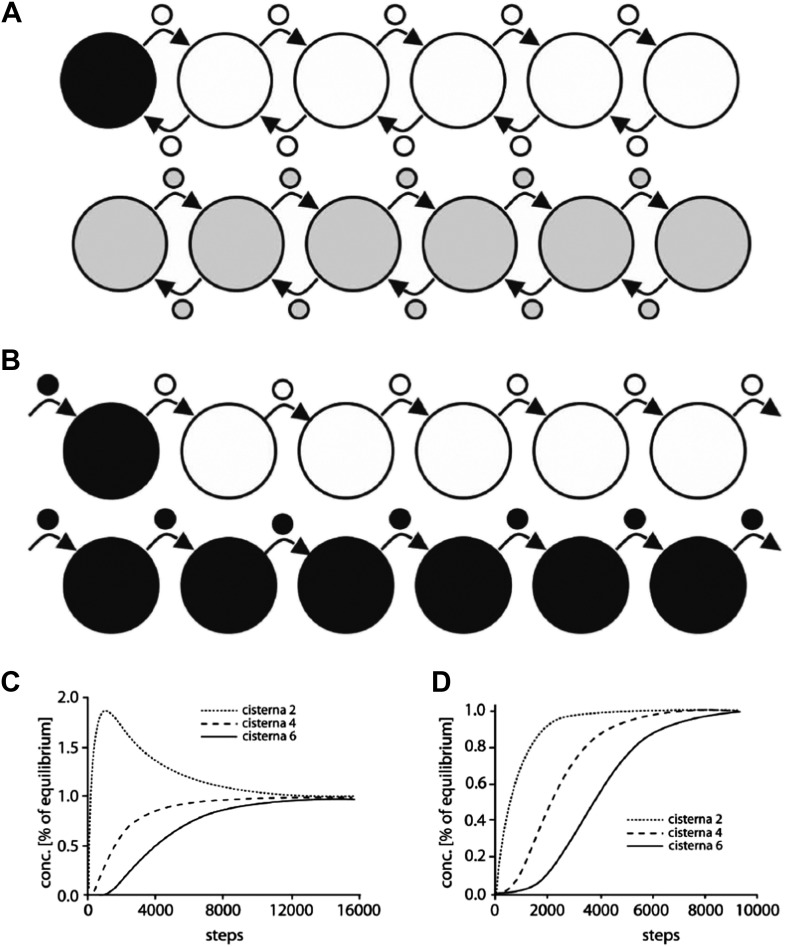
To simulate albumin transport as mediated by vesicles traveling between adjacent cisternae, the geometry of the Golgi cisternae was set to the same parameters as in the standard configuration used for the diffusion model (see Figure 6). Each stack contained 4 to 6 cisternae, each with a diameter of 1.5 microns and a thickness of 30 nm. The vesicles were spherical, with a diameter of 50–70 nm. The simulations started with only the first cisterna filled with albumin (black), and all the others empty (white). Albumin transport is considered to proceed stepwise, where each step is defined as one vesicle detaching from each cisterna and fusing with an adjacent one. The albumin concentration in the vesicles is always assumed to be the same as in the cisterna from where they originated. The albumin concentration in the various cisternae is expressed as a function of the numbers of steps (per cisterna, as defined above). Two scenarios were considered. (A) In the first, cargo is exchanged between the neighboring cisternae by anterograde as well as retrograde vesicles. This means that the first and last cisternae exchange one vesicle each at every step, while the other cisternae exchange two vesicles. This is required for the cisternal volumes to be kept constant. In this simulation, 50% and 90% equilibrium were reached after 3948 and 8846 steps per cisterna, respectively (for comparison, 282 and 933 steps are required for 50% and 90% equilibrium across only two cisternae). For larger vesicles with diameters of 60 nm and 70 nm 90% equilibrium is reached with fewer steps (5119 and 3224, respectively). However, experimental observations indicate a range of vesicle diameter from 50 nm to 70 nm, so for our calculations described below we considered the vesicle diameter to be 60 nm. (B) The second scenario represents the steady-state situation where only anterograde transport vesicles are considered. Here, in each step, one vesicle detaches from each cisterna and fuses with the next one. The volume constancy of the system is maintained by a vesicle coming into the first cisterna at each step (containing the same albumin concentration as the first cisterna), and by an identical vesicle exiting the last cisterna. Here, 50% and 90% equilibrium are reached after 3785 and 6474 steps using 50 nm diameter vesicles (compared to 563 and 1865 steps for only two cisternae). (C and D) Changes in albumin concentration in cisternae 2, 4, and 6, expressed as fractions of the concentrations in the same cisterna at equilibrium, as a function of the number of steps, for the scenarios in A and B, respectively. All these simulations were performed using the MATLAB software and the script Skript3_Golgi_vesicular_transport.m is provided as supporting material.
Based on the above numbers, the model (scenario ‘a’ is considered here and the results are similar also with scenario ‘b’) predicts that close to 5119 vesicle budding/fusion steps per cisterna are required for 90% equilibration of albumin across the stack, considering 60 nm diameter vesicle, 6 cisternae per stack and the concentration of albumin in vesicles as same as that of the cisterna. Our own observations indicate that the concentration of albumin in the vesicles is 20% of that present in cisterna (see Figure 5), so approximately 25,000 steps per cisterna are needed for 90% equilibration of albumin across the stack. Since such equilibration happens in less than 2 min (we consider 2 min here, for simplicity), each cisterna has to bud (and fuse with) close to 12,500 vesicles per min or about 200 per s. Based on these numbers one can calculate the turnover of a cisternal rim assuming that: (A) the diameter of an ‘ideal’ cisterna in the mammalian Golgi to be 1500 nm, and therefore the perimeter of the cisterna to be approximately 4700 nm, and, (B) vesicles are formed from the whole perimeter (or rim) of the cisterna, then a maximum of 78 vesicles of 60 nm diameter (4700/60) can bud from the rim of each cisterna at any given time. Thus, the budding (and fusing) of 78 vesicles can be considered one event of turnover of the cisternal rim. Thus, a rim, in order to produce 12,500 vesicles per min, has to turnover (12,500/78) 160 times per min i.e., once every 400 ms, or in other words, the rim turns over 2.5 times per second. On varying the diameter of the vesicle from 50 to 70 nm this value ranges from 4 to 2 times per second for a stack with 6 cisternae (see Table 2 for the results of these calculations). Since the typical Golgi of the HeLa cells that we used for live imaging studies contained 4 cisternae, we also simulated vesicle-mediated transport across such a Golgi. Based on the results of this simulation described earlier, the calculated turnover rate of cisternal rims varies between 2 and 1 times per second for a stack with 4 cisternae (see Table 2). Thus for a range of parameters used for the simulation (variations in number of cisterna, vesicle diameter and bidirectional or unidirectional vesicle transport), the calculated turnover time of a cisternal rim ranges between 250 and 1000 ms (see Table 2) i.e., turnover of the cisternal rims ranges from 4 to 1 times per second.
Regardless of the mode of intra-Golgi transport, if we match these numbers with published observations about the Golgi, we can then ask whether this vesicle-based turnover rates are possible/realistic or else. Actually, there are a few experimental observations, which, in the light of these calculations, indicate that a role of vesicles in albumin transport is not tenable:
1) One is qualitative and is about the images of budding/fusing vesicles in Golgi stacks observed by electron microscopy. Thus, if each cisternal rim generates 200 vesicles (and fuses with 200 vesicles) per second then one would expect to see signs of this enormous budding and fusion activity at the cisternae. This is, however, clearly not the case. The Golgi cisternae look rather 'quiet', with fairly rare images of budding or fusion.
2) Another observation is quantitative and is based on the association-dissociation rate of the Arf/COPI complex at the Golgi in living cells. The life cycle of a COPI-dependent vesicle is schematically comprised of the following steps: exchange of GDP/GTP on Arf, association of Arf-GTP and COPI with the membrane of cisternal rims, budding, fission, and uncoating of the vesicle (which is initiated by GTP hydrolysis on Arf and the consequent dissociation of Arf from the vesicle membrane), and then docking and fusion of the vesicle with the next cisterna. At the uncoating stage, Arf and COPI are shed from the vesicle and become cytosolic. Thus, the on- and off-rate of Arf/COPI at the Golgi (or at least of the portion of Arf/COPI that is involved in forming vesicles at the rims) should reflect the overall turnover of the vesicles. Hence, if the rimmal membrane turns over (i.e., turns into vesicles and fuses with an equivalent number of vesicles) 2.5 times per second, then the portion of Arf/COPI coat that is located at the rims should cycle, i.e., detach from (and attach to) the rim membrane at the same rate, namely, 2.5 times per second. As noted, these considerations are valid only for the fraction of Arf and COPI that participate in vesicle formation at the rim, rather than for the total Golgi Arf and COPI pool; however, the available evidence indicates that a sizable fraction of the Golgi-associated Arf/COPI is located at the cisternal rims (Oprins et al., 1993; Weidman, 1995). Hence, a substantial portion of the Golgi-associated Arf/COPI pool would be predicted by the vesicular model of albumin transport to associate with and detach from the rimmal membrane 2.5 times per second. Hence, the vesicular model of albumin transport predicts that a substantial portion of Golgi-associated Arf/COPI pool would associate with and detach from the rimmal membrane 2.5 times per second.
The rate of association/dissociation of Arf and COPI with/from the Golgi complex has been measured in living cells by FRAP and FLIP video microscopy (Presley et al., 2002), and its value has been used as a descriptor of the molecular process of Arf and COPI binding to, and dissociating from, the Golgi membrane (Presley et al., 2002). It turns out that the Arf/COPI dissociation/association rate at the Golgi is mono-exponential with a half time of 15 s for Arf and 35 s for COPI, and that similar values apply to the dissociation of Arf/COPI in the presence of BFA (Presley et al., 2002). These rates are orders of magnitude slower than those predicted by the vesicular model of albumin transport (notably, the process underlying these slow rates remains unclear [Presley et al., 2002]). Hence, the major fast cycling subpopulation predicted by the vesicular model of albumin transport is not detected. We conclude that this subpopulation of Arf and COPI does not exist, and that the vesicular model of albumin transport is incompatible with the available data.
These data and arguments rule out, or at least strongly militate against, the possibility that Golgi vesicles turn over fast enough to mediate the rapid intra-Golgi transport of albumin. A further consideration that argues against a vesicular turnover rate as fast as that predicted by the vesicular model of albumin transport is based on the comparison between this predicted rate and the rate that is experimentally observed for the formation of other coated (e.g, clathrin- or COPII-coated) vesicles, in other cellular locations. The rates of formation of these vesicles (Thor et al., 2009) (Steinman et al., 1976) and even of synaptic vesicles at one of the fastest brain synapses (Fernandez-Alfonso and Ryan, 2006), are order of magnitudes lower than those predicted by the vesicular model of albumin transport. Such a difference, while formally possible, would be quite surprising.
Given the above considerations, we conclude that the most parsimonious interpretation of the data is that the bulk of the trafficking of albumin through the Golgi is mediated not by the vesicles but by intercisternal tubules.
Figure 6—figure supplement 2. Computer-simulated model of the formation of a pH gradient between continuous cis- and trans-Golgi cisternae.
(A) The model is based on three proton-handling components in the stack (the size and geometry of which are as defined in the legend to Figure 6): proton pumps located in the trans-most cisterna (cisterna 1: swirls), proton channels located in all of the other cisternae (cisternae 2–6: red circles), and a proton buffering system (made up of proteins and/or lipids; dashes) that decreases the diffusion coefficient of protons moving through the system. For modeling, the initial luminal pH was set to be identical to the cytosolic pH (set at 7.0). When the pumps start working (activity of pumps: 10 protons/s in total; modeled on four pumps), the proton concentration in the lumen of the trans-most cisterna (cisterna 1) starts increasing locally. Protons then start diffusing towards the cis-Golgi pole (cisterna 6). Their diffusion is slowed down by the proton buffering system (proteins and lipids). The diffusion coefficient for protons here is set to 10 µm2/s (for comparison: diffusion coefficient for protons in bulk water is 9.3 × 103 µm2/s [Pines et al., 1988]). Moreover, as the protons move, they encounter the proton channels present in cisternae 2 to 6, through which they can leak out into the extra-luminal space, resulting in a pH gradient across the Golgi stack. The rate of leakage is assumed to be linearly dependent on the difference between the proton concentrations in the lumen and in the cytosol (zero leakage for an internal pH of 7.0, and a leakage of 1.4 protons/s/channel for an internal pH of 6.0; the model assumes two channels per cisterna). The energy needed to generate the gradient comes from the ATP consumed by the proton pumps. The steepness and shape of the gradient depend on the interplay among these three defined proton-handling mechanisms. (B) Time-course of generation of steady-state pH in the cisternae according to this model (final pH of cisternae 1 to 6: 6.00, 6.17, 6.32, 6.45, 6.55, 6.60). (Assuming a diffusion coefficient of 100 µm2/s would result in a proton pump rate of 100 protons/s and a leakage rate of 14 protons/s at an internal pH of 6.0, and the time scale in the Figure would range from 0 to 6 s. The final pH values would not change.)