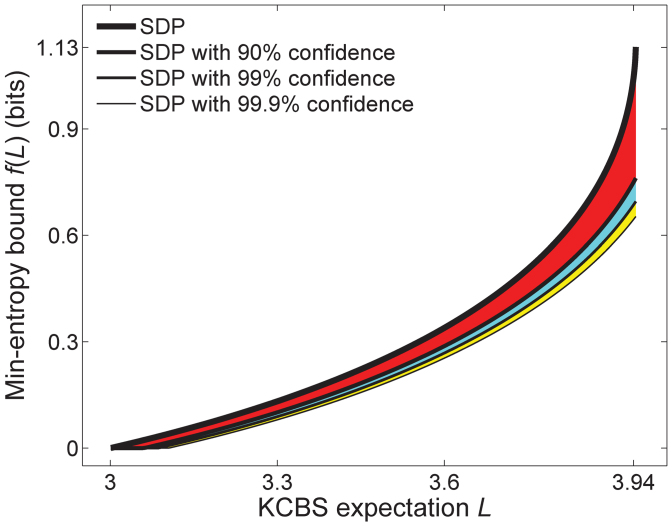
Figure 3. The min-entropy vs. the violation.

The function f(L) in Eq. (8) depending on the violation L of the KCBS inequality (5), which is calculated by semi-definite programming (SDP). The function 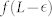at various confidence levels 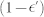such as 90%, 99% and 99.9% are plotted for the uniform choices of measurement configurations, where 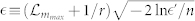and r = min_iP (A_iA_i+1) = 1/5. Here we divide interval with the spacing 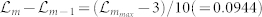. Given a measured 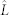and confidence level, we can estimate the min-entropy of a generated random string as summarized in Eq. (8). Note that we ignore the term log₂ δ in Eq. (8) that does not have dependence on the trial n.