The false classification of extinction risk in noisy environments

Abstract

Abundance trends are the basis for many classifications of threat and recovery status, but they can be a challenge to interpret because of observation error, stochastic variation in abundance (process noise) and temporal autocorrelation in that process noise. To measure the frequency of incorrectly detecting a decline (false-positive or false alarm) and failing to detect a true decline (false-negative), we simulated stable and declining abundance time series across several magnitudes of observation error and autocorrelated process noise. We then empirically estimated the magnitude of observation error and autocorrelated process noise across a broad range of taxa and mapped these estimates onto the simulated parameter space. Based on the taxa we examined, at low classification thresholds (30% decline in abundance) and short observation windows (10 years), false alarms would be expected to occur, on average, about 40% of the time assuming density-independent dynamics, whereas false-negatives would be expected to occur about 60% of the time. However, false alarms and failures to detect true declines were reduced at higher classification thresholds (50% or 80% declines), longer observation windows (20, 40, 60 years), and assuming density-dependent dynamics. The lowest false-positive and false-negative rates are likely to occur for large-bodied, long-lived animal species.

1. Introduction

Random processes are a ubiquitous feature of population fluctuations. A variable, stochastic environment may move a population randomly around a true underlying trend in abundance, creating a time series of abundance that is a combination of both deterministic ecological processes (e.g. declining abundance owing to changes in habitat) and stochastic fluctuations [1–5]. Such stochastic variation in abundance, commonly referred to as process noise, can arise when fluctuations in an organism's biotic and abiotic environment cause transient population-wide variations in birth and/or death rates that result in short-term deviations around a true underlying temporal trend in population abundance. Process noise can be further exaggerated when it is positively autocorrelated in time, e.g. when greater-than-average population growth in one year is followed by greater-than-average growth in the following year. Correlated process noise can arise from the abiotic environment, species interactions or age-structured dynamics [2,4–8]. For example, correlated climate variability may lead to positively correlated environmental variation between years, which in turn can lead to positively correlated variation in the birth rates, death rates and abundance of an organism. In theory, this autocorrelation in process noise can thus have important effects on both the magnitude of stochastic variation in abundance and the probability of extinction [4–6,9,10].

In addition to real stochastic changes in abundance from year to year, variation in observed abundance can also arise from imperfect estimation of abundance [7]. This ‘observation error’ (i.e. the difference between true and observed abundance) is inherent in almost all estimates of abundance, except in the rare cases where populations are censused completely (e.g. counts of closely managed species such as the Californian condor). Observation error can either arise from systematic errors (e.g. bias that always underestimates or overestimates true abundance) or random error owing to the sampling process. Observation errors can be particularly large in systems with sporadic or little systematic monitoring.

Estimation and interpretation of the true underlying rate of change in abundance in the presence of process noise and observation error can be challenging. Classification errors can occur where, for example, one either fails to correctly classify a population as declining when it is declining (a false-negative), or incorrectly classifies a population as declining when it is not (a false-positive or false alarm [1,3,9–11]). Such errors particularly arise if the magnitude of stochastic variation in abundance is large, time series of observations are short, or observations are missing—three conditions that are quite common in ecological systems, unfortunately [2,4,5,7,8,12,13]. Population ecologists have devoted much effort to developing quantitative methods to disentangle observation error and process noise from true underlying trends in abundance, including state-space models that jointly estimate observation error along with process noise in time-series data of abundance [4–6].

Stochastic variability can give rise to true increases or decreases in abundance over short time scales, despite the fact that there may be no underlying true long-term trend in abundance (figure 1). If the assessment spans a series of observations coinciding with a transient increase or decrease in abundance owing to process noise, then it is possible to misdiagnose those stochastic deviations in abundance as a true underlying trend. The chance of this occurring is likely to be greater for shorter durations of observations of abundance (shorter relative to generation length) and stronger for positive autocorrelations in process noise (figure 1). Misdiagnosing stochastic deviations in abundance as true underlying declines in abundance (a false-positive error) has practical implications, because management actions to halt or reverse declines in abundance can be expensive, will divert limited resources away from other activities, and ideally would only be taken when there is a decline that will continue unless intervention occurs. This assumes that conservation actions should be based on the long-term status of a population and not on transient changes in abundance owing to stochastic fluctuations. There may be instances where action is warranted even if in the long run a population is stable. For example, small populations have an increased probability of extinction owing to random catastrophic events [9–11]. Failing to detect true underlying declines in abundance (a false-negative) and therefore not taking management or conservation action when it is needed can put species and populations at further risk of extinction and delay their recovery [12,13].

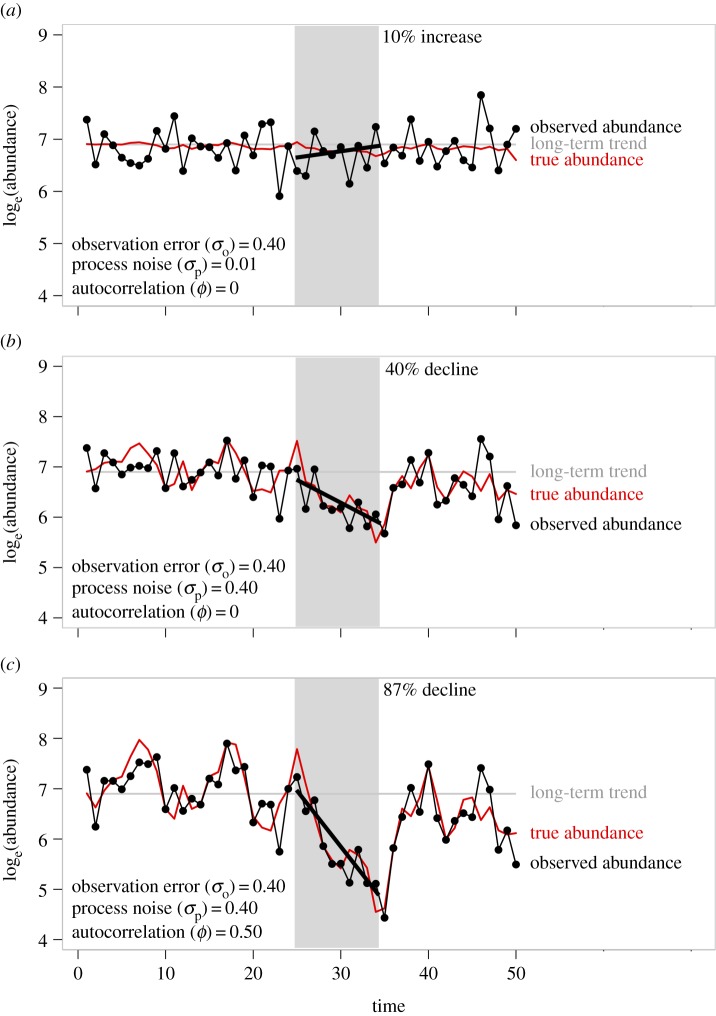
Figure 1.

Three example hypothetical stable time series of abundance (no true underlying time trend) with a starting abundance of 1000 individuals (horizontal grey line). The time series in each panel were generated by setting density-dependence (b in equation (2.1)) to 0.65 and the population growth rate (λ) to 2.4. Variability in the true and observed time series is solely a function of lag-1 autocorrelated (ϕ) process noise (∼N(0, σ_p)) and observation error (∼N(0, σ_o)), the latter only for the observed time series; see lower left corner of each panel for values of these parameters. Closed circles and thin black line are observed abundance, whereas the red line without symbols is the underlying true stochastic abundance (state). The thick black lines are least-square linear regressions of the relationship between log_e abundance and time for time steps 25–34; the corresponding estimated per cent change in raw abundance over the 10 years is shown at the top of panels (a–c). These panels illustrate that despite a long-term stable trend in abundance, quantifying trends in abundance over short time scales may lead to falsely classifying the population as decreasing in abundance, especially at high magnitudes of process noise (b,c), and lag-1 autocorrelation in process noise (c).

Which classification errors should we care most about? Some decision-makers might be most concerned with the potential social and economic costs of false-positives (implementing actions when they were not necessary), whereas others might be most concerned with the biodiversity costs of false-negatives (failing to act when one should), arguing that there is often little cost to falsely declaring a species as being at risk of extinction. However, this is true only when budgets for conservation actions are unlimited (i.e. never), and when conservation occurs in isolation of other societal values. Moreover, the conservation imperative is increasingly being challenged by resource exploitation. Regardless of whether one is more concerned with false-negatives or false-positives, few would argue against the need for accurate estimates of extinction risk. Indeed, an adequate understanding of the factors that are most likely to lead to erroneous conclusions about extinction risk in either direction is an important prerequisite for making informed conservation and management decisions.

Despite the ubiquity of conservation metrics based on trends in abundance, the extent to which stochastic variation in abundance may lead to classification errors has only been quantified for a few taxonomic groups [1–5,14,15] or under high and low empirical estimates of uncorrelated process noise and observation error [6,16]. To the best of our knowledge, this previous work has not considered the potential influence of temporal autocorrelation in process noise. In addition, the conservation focus on false-negatives by many researchers has created a gap in our understanding about false-positives. Here, we ask ‘to what extent does autocorrelated stochastic variation, which may exist in a broad range of taxa, lead to false-positives that classify populations as having increased risk of extinction and to false-negatives that fail to identify those populations that are at risk?’ Our goal is to provide general insights into the extent of potential misclassification of threat status in conservation and resource management contexts. We do this by estimating empirical bounds on the magnitude of autocorrelated process noise in nature (across the global population dynamics database, GPDD), and the degree to which both autocorrelated process noise and observation error are expected to influence false-positive and false-negative rates.

2. Methods

We first developed simulations to determine the probability of occurrence of: (i) a false-positive, i.e. falsely classifying a stable population as being at risk of extinction (i.e. declining more than a given threshold), and (ii) a false-negative, i.e. a declining population as not at risk (i.e. declining less than a given threshold). We explored how these probabilities are affected by a wide range of values of: (i) process noise, (ii) magnitude of temporal autocorrelation in that process noise, and (iii) observation error. We then fitted state-space models using a Bayesian estimation framework to empirically observed field abundances of numerous taxa to estimate the typical range of parameter values for: (i) process noise, (ii) autocorrelation in process noise, and (iii) observation error. Finally, we examined the results of our simulations within the bounds of those empirical parameter values to understand the probability of falsely classifying extinction risk in real-world populations. We describe these steps in detail below.

(a). Simulated time series

We simulated time series of abundance according to a stochastic Gompertz model of population dynamics [9,10,17], which is useful in many conservation applications because its parameters can be estimated directly from time series of abundance estimates, data which are more common than the detailed demographic information necessary for more complex models of population dynamics:

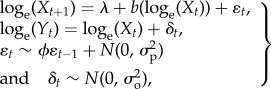2.1

where X_t is the true abundance in year t, λ is the population growth rate per time step, b is the strength of density-dependence (i.e. when b is equal to 1, the dynamics are density independent, and when b is less than 1, they are negatively density-dependent), ɛ is process noise that is correlated with the previous year's process noise through the lag-1 autocorrelation, ϕ, Y_t is observed abundance in year t and δ is observation error. Both process noise and observation error were assumed to be normally distributed, with a mean of zero and variance equal to 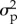and 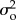, respectively [2,4,5,18]. The process model in equation (2.1) is analogous to an autoregressive moving average model ARMA (1,1), where the autoregressive process noise (ɛ) is the moving average component and b represents the first order autoregressive (AR(1)) coefficient [6,19].

To estimate the false-positive rate, we generated a stable time series with no true underlying time trend by setting b equal to 0.65 and the population growth rate λ to 2.4. The resulting time series consisted of observed abundance Y and true abundance X in year t, both which varied solely as a result of ɛ, δ and ϕ. We set b equal to 0.65 because it represents moderate density-dependence and is the median estimate of the strength of density-dependence from previous state-space analyses of the GPDD [9,10,20]. We repeated those simulations assuming density-independent dynamics (b = 1, λ = 0). To estimate the false-negative rate, we repeated the procedure above except with three true underlying time trends (a total decline of 30%, 50% and 80%) over a range of observation windows. For these declining time series, we assumed density-independent dynamics [14] and population growth rates (λ) less than 0 for each of the 12 combinations of total decline and observation window (see the following section for the λ values corresponding to each rate of decline in log_e space).

To explore the joint influence of observation error, process noise and temporal autocorrelation in process noise (at a one-time-step lag) on our ability to correctly classify a population as stable (i.e. defined as where the slope of the relationship between abundance and time is not significantly different from zero), we simulated 10 000 time series, 100 time steps long, each starting with a true abundance of 1000 individuals. These simulations were run for each of 400 possible combinations of observation error (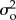; 0.1, 0.3, 0.5 and 0.7), process noise (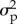; range: 0–2 in steps of 0.2) and autocorrelation in that noise (ϕ; range: −1 to 1 in steps of 0.2) for a total of 4.84 million time series.

To explore how the same sources of variability in abundance outlined above influence our ability to correctly classify a population as declining (i.e. reject the null hypothesis that a population is not declining enough to be considered vulnerable, threatened or endangered when in fact it is at least as much), we simulated time series with three underlying time trends (a total decline of 30%, 50% and 80%) over 10, 20, 40 and 60 time steps across the same 400 possible combinations of observation error, process noise and autocorrelation in process noise that we considered for the above analysis of false-positives.

(b). Classifying population trends

(i). The probability that stable noisy populations are misdiagnosed as declining (false-positives)

For each simulated time series, we randomly selected a 10, 20, 40 or 60 year observation window (i.e. duration of time series over which a time trend is estimated). We fitted an ordinary least-squares linear regression to the resulting time series of observed log_e abundance to estimate the rate of change (i.e. slope) in abundance over the observation window. For each combination of observation error, process noise, lag-1 autocorrelation and observation window, we calculated the proportion of the 10 000 simulations in which the population might be misclassified as at risk of extinction according to the International Union for Conservation of Nature (IUCN) red list decline criterion A2 [1,3,21]. Specifically, for three situations, we calculated the proportion of simulations where the slope was significantly (at α = 0.1) less than: (i) −0.035, −0.018, −0.009 and −0.006 log_e abundance per time step, which correspond to a decline in abundance of at least 30% over 10, 20, 40 and 60 years, respectively, and an IUCN classification of vulnerable (high risk of extinction); (ii) −0.069, −0.035, −0.017 and −0.012, which correspond to a decline in abundance of at least 50% over 10, 20, 40 and 60 years, respectively, and an IUCN classification of endangered (very high risk of extinction); and (iii) −0.161, −0.081, −0.040 and −0.027, which correspond to a decline in abundance of at least 80% over 10, 20, 40 and 60 years, respectively, and an IUCN classification of critically endangered (extremely high risk of extinction).

(ii). The probability that declining noisy populations are misdiagnosed as stable (false-negatives)

For each of the 10 000 iterations under each scenario of true declining abundance (i.e. a total decline of 30%, 50% or 80%), we calculated the estimated rate of decline as described above for false-positives. We then quantified the false-negative rate as the proportion of simulations where we failed to reject the null hypothesis (i.e. not declining enough to be considered vulnerable, threatened or endangered), when in fact the null hypothesis was false.

(c). Empirical estimates of correlated process noise and observation error

To generate empirically plausible estimates of observation error, process noise and the degree of autocorrelation in process noise, we analysed 627 abundance time series from the GPDD [2,4,5,7,8,22]. The GPDD is one of the most comprehensive collections of abundance time series in the world and consists of nearly 5000 time series. We filtered these data series to remove plant populations, non-annual sampling intervals, time series shorter than 15 years (median: 26 years; range: 15–156), and harvest-based estimates of abundance that assume harvest is an index of abundance, resulting in 627 unique time series across four classes, 19 orders and 362 species (see the electronic supplementary material for full list of time-series IDs from the GPDD).

We fitted five variations of the model defined in equation (2.1) to each of the GPDD time series in a Bayesian estimation framework (table 1). By fitting these models within a Bayesian framework, as opposed to maximum-likelihood, we avoided the problem of boundary estimates of process noise and observation error from time series in the GPDD that result in failure of the models to converge [4–6,16,23], because even weakly informative priors can keep models from failing to converge.

Table 1.

The five variations of the Gompertz population dynamics model in equation (2.1) that were fitted to each of the global population dynamics database time series using a Bayesian estimation framework. (Parameters that were estimated are denoted by ‘est.’. Remaining parameters were fixed at either zero or one.)

model	process noise (σp)	observation error (σo)	growth rate (λ)	density-dependence (b)	autocorrelation in process noise (ϕ)
1	est.	est.	0	1	0
2	est.	est.	0	est.	0
3	est.	est.	est.	1	0
4	est.	est.	0	1	est.
5	est.	est.	est.	est.	0

We did not fit a model that simultaneously estimated all parameters, because preliminary analyses indicated that such a model routinely failed to converge. This result was not surprising, given that for many time series, especially declining ones, it is very difficult to simultaneously estimate the population growth rate (λ) and density-dependence (b). We therefore took a multi-model inference approach to generate estimates of autocorrelated process noise and observation error that accounted for model uncertainty by weighting parameter estimates from each model by the data support for the model in which the parameters occurred. We quantified that data support for each of the five models using the deviance information criterion (DIC) and then calculating normalized DIC model weights based on DIC differences from the top model, i.e. the model with the lowest DIC [9–11,24]. We then generated averaged parameter estimates, which were weighted averages across models, by multiplying the median posterior probabilities of each parameter (or fixed value) by the normalized DIC weight of the model in which the parameter occurred and then summing these weighted parameter estimates across the five models for each time series [12,13,25,26].

We assigned uninformative gamma (10⁻³, 10⁻³) prior probability distributions to 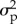and 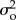, an uninformative normal (0, 1) prior to λ, and uniform priors to b (0, 2) and ϕ (−1, 1). Posterior probability distributions were generated for the parameters estimated in each model using a Markov chain Monte Carlo procedure in the JAGS package in R [1,3,14,15,27]. We ran three chains for 100 000 iterations, and thinned every five iterations with a burn-in of 5000 iterations. Convergence was assessed by examining the potential scale reduction factor 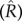; convergence was assumed to have occurred if 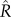was less than 1.1 [16,28].

(d). Mapping empirical estimates of correlated process noise and observation error onto simulated parameter space

The empirical estimates of observation error, process noise and the degree of autocorrelation in process noise from each time series of real-world populations were then mapped onto the parameter space generated in the simulations. Time series with estimated observation error in four categories (i.e. between 0–0.2, 0.2–0.4, 0.4–0.6 and more than 0.6) were mapped onto the simulated parameter space in which the observation error was fixed at either 0.1, 0.3, 0.5 or 0.7. The results visualize, for a broad range of typical taxa, the extent to which variation owing to observation error, process noise and autocorrelation in process noise may lead to the false classification of: (i) a stable time series as being at elevated risk of extinction, or (ii) a declining time series as not being at risk of extinction. Those false classification rates were also estimated across a range of duration of time series and thresholds for extinction risk.

3. Results

(a). Classifying population trends from simulated time series

Noisy time series and observation error led to substantial classification errors of both false-positives (false alarms) and false-negatives. The proportion of simulations where a population was falsely classified as at risk of extinction (when it was actually stable, i.e. false-positive error) was positively related to the magnitude of process noise and positive lag-1 autocorrelation in that process noise (figure 2a,b). The false classification rate was much lower in density-dependent (figure 2a) than density-independent populations (figure 2b). These lower false-positive rates arise because simulated population dynamics without density-dependence result in abundance that follows a random walk, whereas the dynamics of populations with density-dependence will tend to have dampened positive and negative deviations in abundance from the carrying capacity of the population (i.e. the long-term stable abundance). In contrast to false-positives, when observation windows were short, false-negative rates for a truly decreasing population increased as the lag-1 autocorrelation in that process noise became more negative (figure 2c and the electronic supplementary material, figure S1—10 years). However, when datasets were lengthy, false-negative rates increased with increasing process noise and larger positive lag-1 autocorrelation (electronic supplementary material, figure S1—60 years).

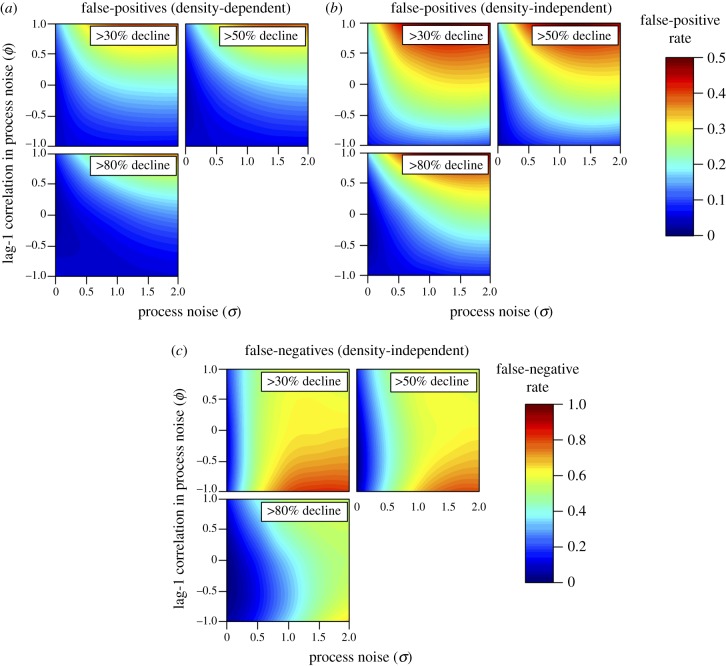
Figure 2.

Relationship among process noise (in standard deviation units), the magnitude of lag-1 correlation in process noise, and the probability (shown as coloured contours) of falsely classifying a stable population as being at increased risk of extinction (panels a,b; greater than 30%, 50% or 80% decline in abundance over 10 years, as shown in each subpanel) or failing to correctly classify a declining population as at risk of extinction (c; true decline in abundance over 10 years of 30%, 50% or 80%, as shown in each subpanel). The false-positive and -negatives rates are based on a linear regression with α = 0.1, a time series 10 time steps long, and observation error equal to 0.1 standard deviation units. False-positive rates are based on (a) simulated time series with moderate density-dependence (b = 0.65) and a population growth rate equal to 2.4 (λ; see equation (2.1)), or (b) density-independent dynamics (b = 1, λ = 0), whereas false-negative rates are based on (c) density-independent dynamics (b = 1, λ = rate of decline in subpanel).

Large-magnitude process noise that was strongly positively autocorrelated (but not negatively autocorrelated) led to the highest probabilities of false-positives, regardless of the threshold for classifying a population as being at risk of extinction and whether the population had density-dependent or density-independent dynamics (figure 2a,b). That general result also held for all observation windows and magnitudes of observation error (electronic supplementary material, figure S2). This pattern arises because positively autocorrelated process noise results in larger departures from an underlying trend than the dampening, regulating effect of negatively correlated noise. With positive autocorrelation, each stochastic deviation in abundance is more likely to be in the same direction as the deviation in the previous time step.

(b). Empirical estimates of correlated process noise and observation error

Real-world animal population abundance time series are characterized by greater observation error than process noise (figure 3). The distributions of estimates of both parameters were characterized by long tails, indicative of a few time series with large estimates, whereas the majority of parameter estimates fell near the medians of 0.18 and 0.41 standard deviation units for process noise and observation error, respectively (figure 3). In contrast to the support for process noise and observation error, there was less evidence for widespread autocorrelation in process noise; half the time series had multi-model averaged estimates of lag-1 autocorrelation in process noise equal to zero (357 of 627 time series; figure 3).

Figure 3.

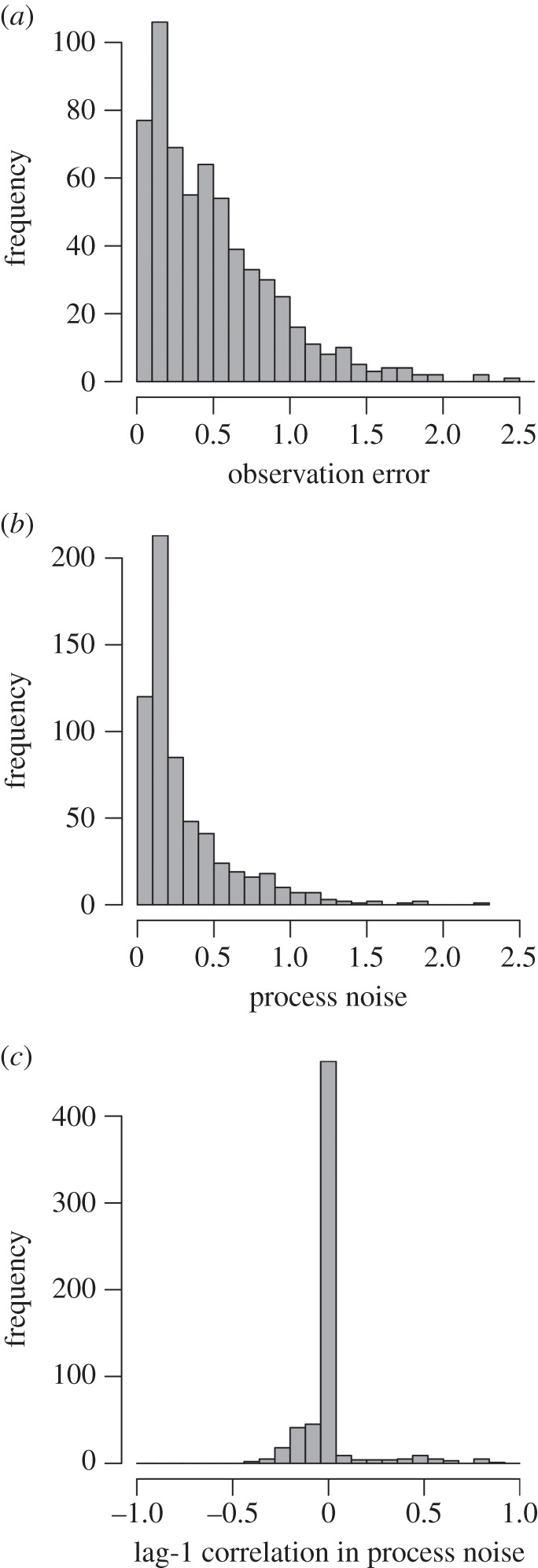
Histograms of estimated median posterior probabilities for (a) process noise (in standard deviation units), (b) observation error (in standard deviation units), and (c) magnitude of lag-1 autocorrelation in process noise from 627 time series of animal abundances from the global population dynamics database. The histograms in (a) and (b) are truncated at 2.5 on the x-axes; as a result, one estimate of process noise and three estimates of observation error are not shown.

(c). Mapping empirical estimates of correlated process noise and observation error onto the simulated parameter space

Most of the animal abundance time series were characterized by combinations of observation error and process noise (some of which was autocorrelated) that corresponded to a false-positive rate of approximately 0.1–0.2, and no greater than 0.3 (i.e. no circle within the yellow or red zones of figure 4a) assuming moderate density-dependence (b = 0.65), short time series of observations (10 years) and the classification threshold of a 30% decline (figure 4a). False-positives were reduced when trends were measured over longer time series, and when higher thresholds were used for classifying a stable population as at increased risk of extinction (figure 5a). As a result, at higher thresholds for classification of increased risk of extinction (IUCN A1 of 50% versus IUCN A2–4 of 30%), fewer time series were characterized by the kind of variation that would be expected to lead to false-positives for the classification of extinction risk (figure 5a and the electronic supplementary material, figure S2). Density-dependent populations are less likely to suffer false-positive classifications than those with density-independent dynamics, given the autocorrelated process noise and observation error characterized in the GPDD time series (compare figure 5a with figure 5c).

Figure 4.

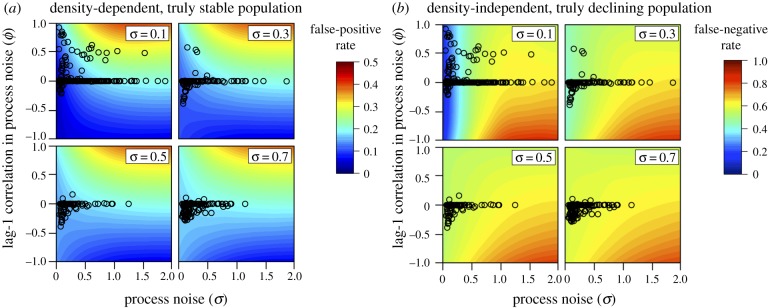
Probability (coloured contours) of (a) falsely classifying a stable population as being at high risk of extinction (i.e. greater than 30% decline in abundance over 10 years) or (b) failing to correctly classify a declining population as at high risk of extinction (i.e. a 30% decline in abundance over 10 years) across a range of process noise (in standard deviation units), lag-1 autocorrelation in process noise, and observation error (in standard deviation units; sigma in the upper right corner of each plot). Empirical estimates of observation error and correlated process noise are based on time series from the global population dynamics database and are mapped onto each panel as open circles.

Figure 5.

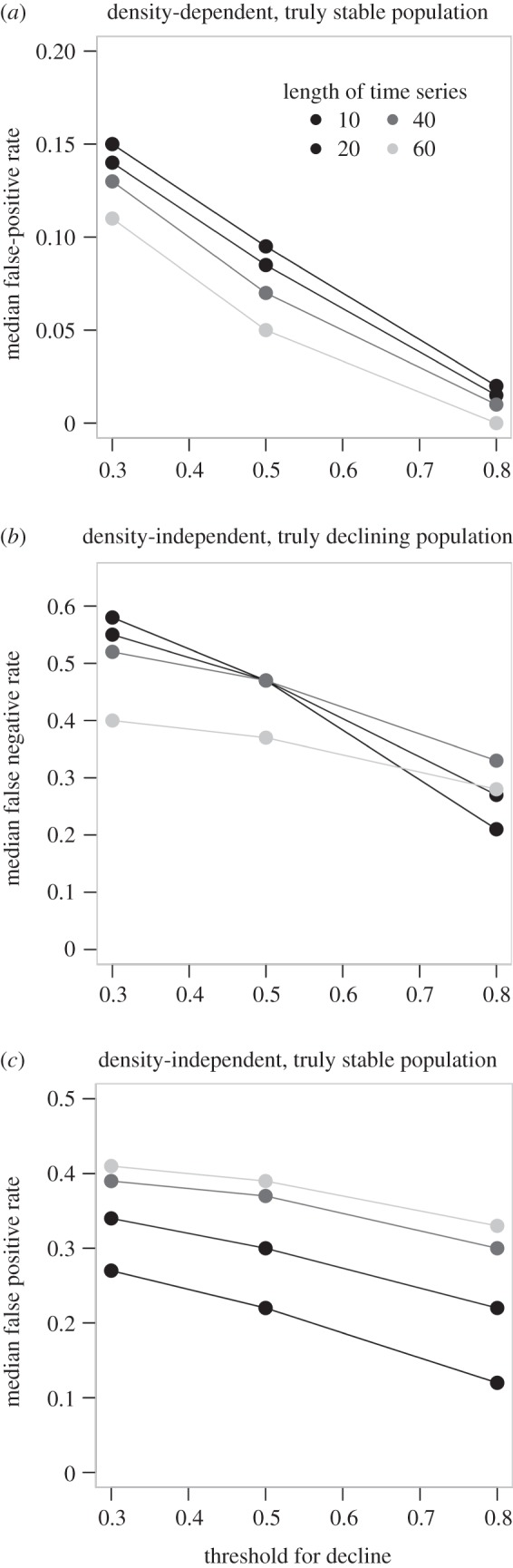
Predicted median false-positive (a,c) and false-negative (b) rates based on simulations that assumed the estimated magnitude of autocorrelated process noise and observation error for each of the 627 time series of population abundance from the global population dynamics database; note the different scales. Data are plotted over a range of observation windows (number of years of data) and thresholds for classification as being at risk of extinction (x-axis, fractional decline in abundance over observation-window years). The predicted classification errors are based on simulations assuming either density-dependent (a) or density-independent (b,c) dynamics.

When considering false-negatives, the empirical time series were characterized by combinations of observation error and process noise that resulted in a false-negative rate of approximately 0.5–0.6, assuming 40 years or shorter time series of observations and the least biologically conservative classification threshold of a 30% decline (figure 5b). Similar to false-positives rates, false-negatives were reduced when trends were measured over longer time series, and when higher thresholds were used for classifying a population as at increased risk of extinction (figure 5b). Interestingly, false-negative rates declined more quickly with increasing classification thresholds for short observation windows than longer observation windows (e.g. 10 versus 60 years in figure 5b).

The effect of duration of datasets on the false-positive rate depended on whether the population dynamics included density-dependence. Over the range of time series lengths we considered, longer time series of data available for decision-making reduced the chance of false-negatives in density-independent simulations (electronic supplementary material, figure S1) and false-positives in density-dependent simulations (electronic supplementary material, figure S2). The influence of time-series length was much more pronounced for false-negatives with density independence than false-positives with density-dependence (compare electronic supplementary material, figures S1 and S2). In contrast to simulations with density-dependence, the false-positive rate increased with the length of the time series over which the decline is estimated in density-independent simulations (electronic supplementary material, figure S3). This result arises because population dynamics in the density-independent simulations are a random walk, and so the longer the time series, the more opportunity there is for population abundance to randomly wander from the long-term mean. Increasing observation error also very slightly increased the probability of falsely classifying a stable population as at risk of extinction (electronic supplementary material, figure S2) and failing to detect a true decline (electronic supplementary material, figure S1) across all combinations of process noise, autocorrelation in process noise, length of time series and threshold for classifying a population as being at risk of extinction.

4. Discussion

Three key findings emerge from our simulations and analyses of false classifications of extinction risk in animal populations. First, stable real-world populations might be misclassified as declining and at risk more often than is typically assumed, that is, with a probability more than 0.1. Using higher decline thresholds can reduce the chance of such false alarms, but this comes at the potential cost of a greater chance of false-negatives occurring, (i.e. not identifying populations that are truly declining) and thus delaying needed conservation or management action. Second, the magnitude of density-dependence is critical; all other things being equal, false alarms are less likely to occur in strongly density-dependent populations compared with weakly regulated populations. Third, at least for the 627 animal populations that we considered, lag-1 temporal correlation in process noise is less prevalent than no autocorrelation. This fact implies that dynamics of most of these populations are not generally driven by substantial external forcing that is lag-1 autocorrelated.

Our work has implications for ranking conservation activities in an era of increasing financial austerity. In the face of reduced budgets [17,29], and increasing pressure for the judicious use of dwindling resources to conserve the world's biodiversity [30], our findings highlight that conservation actions based on trends in abundance alone may, under some circumstances (i.e. classification thresholds of 30% and populations with weak density-dependence), inappropriately direct limited funds to populations that are not truly at risk of extinction.

We recognize that trends in abundance are only part of the threat classification process, which can also include consideration of geographical range and extent of habitat loss and fragmentation as well as quantitative analyses of extinction risk (e.g. population viability analyses; [21]). In addition, we also recognize that falsely classifying a stable population as at risk of extinction may be acceptable under some circumstances. For example, we often do not know during a decline in abundance if that change is owing to short-term stochastic fluctuations or a longer-term trend. As a result, taking action when a population is experiencing a dramatic decline in abundance (even if it is driven by short-term stochastic variability in abundance) may be worthwhile if it nudges a population toward its equilibrium abundance more quickly than if intervention were not taken, or reduces the vulnerability of the population to stochastic events that may lead to extinction.

The cost of falsely classifying a population as at risk of extinction will be context-dependent, will depend on whether the detection of a decline triggers management action (and what type) and is likely to vary by taxa. For example, actions aimed at reversing declines and reducing exploitation opportunities may result in substantial socio-economic costs for those taxa that are harvested commercially. On the other hand, for species that are not commercially exploited, the socio-economic cost of a false alarm may be relatively low. However, false-positives are only part of management decisions that need to balance both the costs of falsely declaring a population in need of conservation action and the costs of falsely declaring a population as healthy (i.e. when, in fact, it could benefit from some form of intervention) [31,32]. Our results highlight that conservation actions based on trends in abundance alone may also fail to correctly identify populations at risk of extinction more often than 50% of the time when based upon short time periods of observation and the least biologically conservative classification threshold of a 30% decline.

Our findings suggest that false alarms may be lowest for the species we are most likely to be concerned about. Conservation and resource management tend to focus on large-bodied species, which generally have low population growth rates and strong density-dependence [33–35]. Although there are exceptions, density-dependence tends to be strongest in large-bodied species, such as mammals, sharks and teleost fishes [36–38]. Thus, because our simulations suggest that false alarms will be lowest in density-dependent populations, the chance of falsely classifying a species or population as at risk of extinction is likely to be lowest in large-bodied species, which also tend to be most targeted for exploitation. We caution, though, that for populations which are heavily influenced by environmental conditions and are largely not regulated by density-dependence, such as small pelagic clupeid fishes, there may be a higher probability of a false classification of threat status (i.e. false-positives and -negatives).

Direct comparison of our results with those from previous studies is difficult, because previous work has used various thresholds and criteria for defining population status. Nonetheless, our finding that the false classification of extinction risk is greater than expected based on chance alone for many populations is generally consistent with previous estimates of the probability of false-positives based on empirical estimates of observation error and process noise from the GPDD [16] and with simulations using age-structured populations of Australian fishes [14]. Previous empirical analyses of exploited populations revealed a zero probability of false classification when species are fished aggressively (i.e. near the limit reference point B_lim, as was typical in Europe until recently; [3]). However, false classifications are present, albeit at low levels, when species are more biologically conservatively managed around the target reference point of B_MSY (as mandated in the USA and increasingly in Europe; [39]). Nonetheless, both these findings illustrate that current IUCN-like threat classifications based on estimated declines in abundance are consistent with, and complimentary to, risk assessments based on traditional fisheries reference points, even though the two are based on very different premises. This is not surprising, because exploited populations tend to exhibit strong density-dependence (which is the defining attribute of a high-yielding fishery, for instance) and are well-monitored with long time series—two key attributes that minimize the chance of false classification of extinction risk.

As is inevitable when analysing a large dataset and assuming simple population dynamics, there are three main caveats to our analyses and interpretations. First, we modelled correlated process noise as an AR(1) in which correlation decreases exponentially with increasing time lag. Although this is a common way to characterize correlated process noise, process noise may show a slower decline in correlation with increasing time lag than assumed by an AR(1) process [6,9,40]. Although it is likely that some time series in the GPDD are better described by such ‘pink’ noise, it is difficult to estimate pink noise from the relatively short time series available. Not considering correlation at longer time lags should, however, result in lower estimates of false-positive and false-negative rates, because pink noise has been shown to have a similar but stronger influence on the probability of extinction as lag-1 autocorrelated process noise [9].

Second, we fitted scalar (or diffusion approximation) models to simulated and empirical data to estimate changes in abundance through time. Scalar models assume there is no underlying age-structure, which may overestimate variability in population size [41]. In our case, we do not have sufficient information to tailor each specific model to include age structure, so our estimates of process noise should be considered precautionary (i.e. biased high for age-structured populations). Third, while our empirical estimates of stochastic variation in abundance are derived from 600-plus time series spanning 300 species, they are still not a random sample of species [42]. The use of these time series may bias our estimates of stochastic variation in unknown directions, but is most likely to result in the inclusion of populations characterized by low stochastic variation in abundance because they are the populations that will have persisted long enough to be studied and incorporated into the GPDD. These caveats and limitations identify room for future analyses to extend the ideas and analyses detailed in this paper. For instance, future analyses could include different types of correlation in process noise at longer time lags, age-structured dynamics with varying degrees of density-dependence and population growth, as well as additional time series of abundance.

In conclusion, our analyses suggest that given the magnitude of correlated process noise and observation error typical of many living organisms, it is possible that stable animal populations will be falsely classified as being at high risk of extinction and declining populations may be falsely classified as being not at risk. However, this is least likely to be true for those populations we might be most concerned about, such as exploited mammals and fishes. Both taxa, especially the larger individuals and species favoured by hunters and fish harvesters, tend to exhibit strong density-dependent survival, which our analyses indicate tends to dampen stochastic variability in abundance, thereby enhancing our ability to detect meaningful trends that require prioritization and action.

Funding statement

We thank the Canada Research Chairs programme in Ottawa and the Natural Science and Engineering Research Council of Canada for funding.