Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Jun 27;4:5471. doi: 10.1038/srep05471

An NCN-pincer ligand dysprosium single-ion magnet showing magnetic relaxation via the second excited state

Yun-Nan Guo 1,3, Liviu Ungur 4, Garrett E Granroth 5, Annie K Powell 6, Chunji Wu 2, Stephen E Nagler 5, Jinkui Tang 1,a, Liviu F Chibotaru 4,b, Dongmei Cui 2,c
PMCID: PMC4073120  PMID: 24969218

Abstract

Single-molecule magnets are compounds that exhibit magnetic bistability purely of molecular origin. The control of anisotropy and suppression of quantum tunneling to obtain a comprehensive picture of the relaxation pathway manifold, is of utmost importance with the ultimate goal of slowing the relaxation dynamics within single-molecule magnets to facilitate their potential applications. Combined ab initio calculations and detailed magnetization dynamics studies reveal the unprecedented relaxation mediated via the second excited state within a new DyNCN system comprising a valence-localized carbon coordinated to a single dysprosium(III) ion. The essentially C2v symmetry of the DyIII ion results in a new relaxation mechanism, hitherto unknown for mononuclear DyIII complexes, opening new perspectives for means of enhancing the anisotropy contribution to the spin-relaxation barrier.

Acting as a tiny magnets, Single-molecule magnets (SMMs)1 are chemically and physically interesting compounds as a platform on which to build future spin-based devices2,3,4,5,6,7. Recently the enormous potential of lanthanide(III) ions8, and dysprosium in particular9,10,11,12,13, has been recognized as a potential source of both the high spin and high anisotropy required for SMM behavior14,15. The blocking of magnetization for Ln-SMMs arises as a result of strong axiality of ground state, which for ions with odd number of electrons (e.g., DyIII) implies the transversal components gx, gy be dwarfed by axial components gz16,17,18,19,20,21,22. The spin is then forced to undergo reversal through a thermally activated process giving a relaxation which follows an Arrhenius behavior with a barrier Δ. This can be likened to a levee that prevents flooding by water even if one side of the levee is lower than the other (Figure 1). For the barrier of the levee in Louisiana, conforming to the laws of classical physics, the water is not breaking through rather than having to go over the top of the barrier. For a SMM, which is an quantum object, it is a question whether the spins can tunnel (break) through the barrier or can be forced to overcome the barrier.

Figure 1. Barrier levee model for design Ln-SMMs.

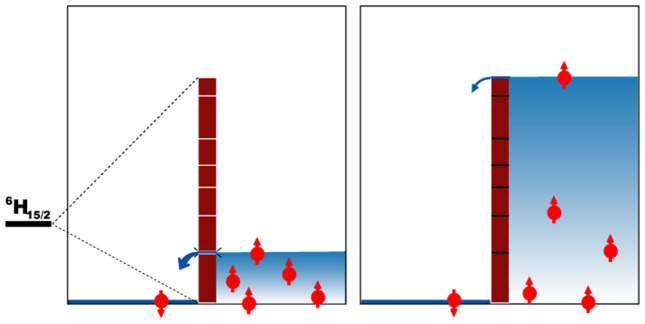
Figure 1

Open in a new tab

With DyIII for example, where the magnetic moment is forced to undergo reversal through a thermally activated process. (Left) Magnetization reversal constrained by the first excited state; (Right) Magnetization reversal forced to the highest excited state.

Breaking through such a levee for a SMM is always constrained by the separation between the bistable ground state and the first excited state23 and arises from the removing the (2J + 1)-fold degeneracy of the ground multiplet provided by the surrounding crystal field (Figure 1, left). The implication to enhance SMM behavior is that we can construct a high levee by elaborating the coordination environment of the lanthanide ions to give suitable constraints to tunneling processes (Figure 1, right). In previous ab initio studies, this scenario was explored by considering an idealized diatomic [DyO]+ complex21. As a result of the perfect axiality of all of the Kramers doublets (KDs) the transversal magnetic field induces a tunneling splitting in [DyO]+ only at the highest order of perturbation theory, following a path similar to that of the reversed double-well potential of Mn12-Ac24. The difference is that, for LnIII ions, the total multiplet width of CF splittings of the order of 100–1000 cm−1 open huge perspectives for means of enhancing the anisotropy contribution to the magnetic relaxation barrier.

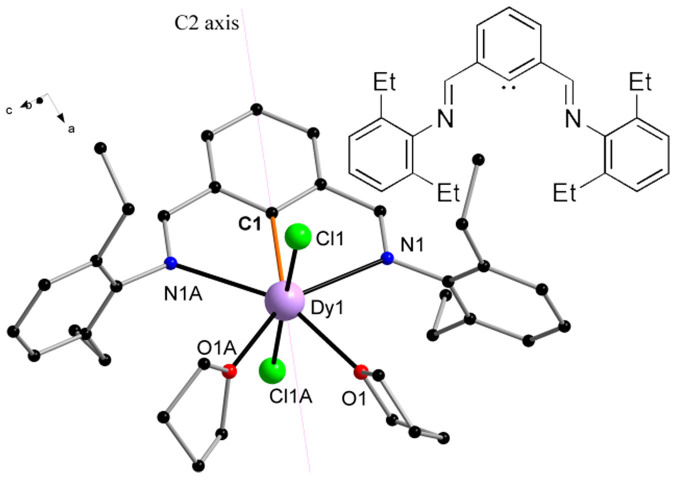
So far a clear-cut example of such a magnetic relaxation via higher excited state energy levels has never been seen before for Ln complexes. Here, we chose to probe the magnetism of a localized Dy-C bond containing complex stabilized by an aryldiimino NCN-pincer ligand (Inset of Figure 2), as exists in [2,6-(2,6-C6H3R2N = CH)2-C6H3]-DyCl2(THF)2 (DyNCN). More striking still, this unique Dy-C bond occupies the crystallographic C2 axis in DyNCN. The combination of ab initio calculations and detailed magnetization dynamics studies reveals the two lowest Kramers doublets being extremely axial in nature and possessing parallel anisotropy axes along C2 direction, which results in the unprecedented relaxation going via the second excited state in compound DyNCN.

Figure 2. Molecular structure.

Figure 2

Open in a new tab

Structure of [2,6-(2,6-C6H3R2N = CH)2-C6H3]-DyCl2(THF)2 (DyNCN) molecule with the Dy-C bond highlighted in orange. Blue, Dy; green, Cl; black, C; blue, N; red, O. H atoms and a THF solvent molecule are omitted for clarity. Complex LuNCN exhibits analogous structure. Coordination bond distances (Å) for DyNCN: Dy-C = 2.3933(25), Dy-Cl = 2.5960(8), Dy-N = 2.6689(24) and Dy-O = 2.4484(20). Inset: The structure of the NCN-pincer ligand [2,6-(2,6-C6H3Et2N = CH)2-C6H3]−.

Results and discussion

X-Ray structure analysis

Compound DyNCN was synthesized via transmetalation between 2,6-(2,6-C6H3R2N = CH)2-C6H3Li and LnCl3(THF)1~3.525, and crystallizes in the space group P43212, with Z = 4. The whole molecule exhibits C2 crystallographic symmetry, in which the Dy–C bond is located on a 2-fold rotation axis [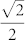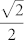Inline graphicInline graphic0]. The monoanionic NCN-pincer ligand coordinates to the central metal ion in a κC: κN: κN' tridentate mode to form a meridional conformation. The two N-aryl rings dispose the vertical positions against the NCN plane, which are parallel to the two cis-located THF rings, respectively. The chloride groups arrange in trans-positions to form a large Cl–Dy–Cl angle (176.500(23)°) bisected by the NCN plane. Therefore, if one focuses only on the atoms of the first coordination sphere two nearly exactly perpendicular planes (C1/N1/O1/O1A/N1A) and (C1/Cl1/Cl1A) are formed. Then the effective CF is of C2v symmetry.

Electronic structure calculations

The interaction of the 4f orbitals involved in the formation of the robust organometallic surroundings seems to play a key role in the LF thereby enhancing the magnetic properties. A few carbon ring coordinated Ln-based SMMs, that include ligands such as cyclopentadienide and cyclooctatetraenide, have generated profound thoughts and enlightenment22,26,27,28,29,30. The discovery of these bona fide organometallic SMMs underscores the significance of making use of the simple Ln-C bond to design molecules with strong axiality31. The title compound with a strong single Dy–C bond combining the huge conjugation effect of a carbanion offers a new paradigm for single ion anisotropy as shown from the ab initio calculated electronic structure of lowest eight Kramers doublets of DyNCN in Table 1 (see Experimental Section and the ESI of Figure S1–S7 and Table S1–S8 for details).

Table 1. Ab initio calculated energies of low-lying Kramers doublets in DyNCN (187 K structure) in units of cm−1.

Free-Ion Multiplet Energy (cm−1) gX gY gZ
  0 9.69E-04 2.12E-03 19.8101
  176 8.72E-03 3.46E-02 17.0586
  262 0.4261 0.4374 19.4439
  348 1.9619 2.5423 12.8581
6H15/2 445 8.0980 7.2355 5.4345
  526 0.4681 0.6001 14.0454
  597 0.5562 0.6565 19.4099
  645 5.87E-02 0.2346 19.3829
Open in a new tab

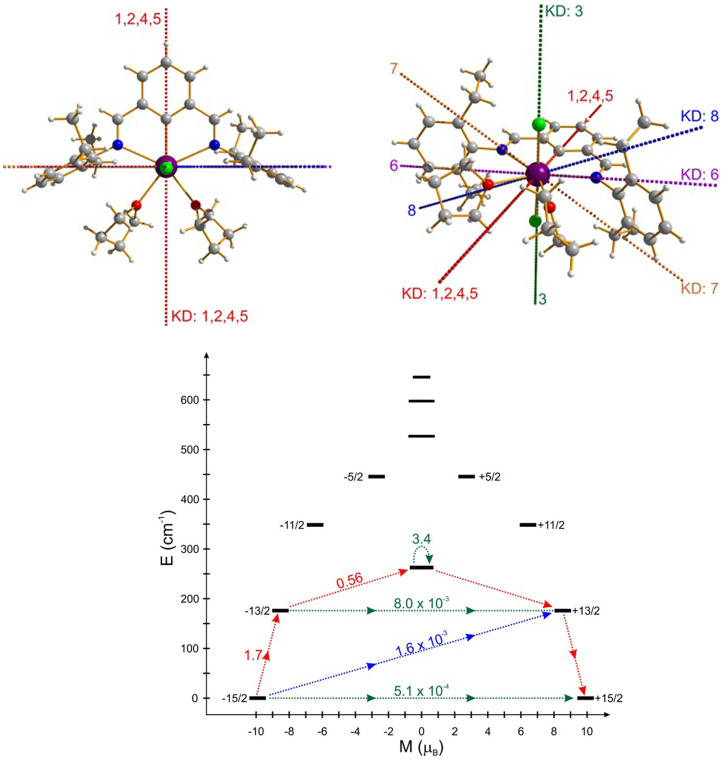
Table 1 shows the low lying spin-orbit energy spectrum of the DyNCN molecule in the largest computational model. We notice a large energy separation of the ground and first exctied Kramers doublets. As shown in Figure 3, the main anisotropy axis of the complex passes along the main symmetry axis of the complex, i.e. it is parallel to the Dy-C chemical bond. The reason for the strong effect of the ligating C atom is the fact that it holds a negative charge as the ligand is a carbanion. The calculated Mulliken charge on the carbon atom revealed a negative charge of −1.17 on the ligating carbon atom. The localized character of the negative charge is probably due to intramolecular electrostatic effects: the negative charge of the carbanion is attracted by positively charged DyIII ion, and the ligating C atom is the closest point to the DyIII ion. This is also the reason why the Dy-C bond is unusually short (≈2.39 Å). Even though the computed Mulliken charges on both chlorine atoms are slightly larger (−1.60), the longer Dy-Cl distances (≈2.60 Å) make the cumulative (total) effect of both chlorine atoms less important for the magnetic anisotropy of the two low lying Kramers doublets than the influence of the much closer carbon atom. In fact, we have already seen for other complexes that the main anisotropy axis is mainly oriented by the effect of the closest ligand21.

Figure 3. Low-lying electronic structure for DyNCN.

Figure 3

Open in a new tab

(Top) Anisotropy axes in eight lowest Kramers doublets at the Dy site of DyNCN (KD: 1–8 ranked in order of the energy from ground state to the seventh excited state as shown in below scheme). The red dashed line corresponds to the anisotropy axis of KD: 1, 2, 4 and 5; the green dashed line shows the anisotropy axis of the second excited KD (KD 3 lying at 262 cm−1). (Bottom) Magnetization blocking barrier of the DyNCN. The black lines represent the energy levels of the ground multiplet J = 15/2 aligned according their magnetic moment on the C2 symmetry axis. The arrows represent the averaged matrix element of the transversal magnetic moment connecting the corresponding states, given as (|μx| + |μy| + |μz|)/3. The red arrows show the most probable path for the magnetic relaxation at high temperatures.

As a result of the above described effects, we notice an interesting fact of collinearity of the main anisotropy axes in the ground (almost pure ±15/2) and first excited (almost pure ±13/2) doublets. We will see later that, the collinearity of anisotropy axes is a key factor for enhancing the magnetic blocking performance of this compound.

Analysing further the magnetic anisotropy of the second excited KD (262 cm−1) we notice that it is again very axial, i.e. of ±15/2 type, but its main magnetic axis is perpendicular to the main symmetry axis of the complex, passing through the two chlorine atoms. The third, fourth and fifth excited KDs are less axial, while the sixth and seventh excited KDs are again highly axial, with their main anisotropy axis lying in the plane perpendicular to the main symmetry axis of the complex21.

Table 2 shows the parameters of the crystal field acting on the ground atomic multiplet J = 15/2 of the DyIII ion. We notice that, although the ab initio calculation was performed in the C1 point group (i.e. effectively ignoring the symmetry) the departure from the perfect point group symmetry is very small, leading to the fact that only parameters of the even projection on the quantization axis enter in the decomposition of the ab initio energy matrix. The largest parameter, 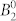Inline graphic sets the main anisotropy axis of the ground and of the first excited KD, while the significant value of the second largest parameter, 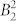Inline graphic, is probably responsible for the anisotropy of the second excited KD. In other words, the Inline graphic parameter is the largest in the case when the quantization axis is parallel to the main anisotropy axis of the second excited KD, i.e. passing along the Cl-Cl axis.

Table 2. Ab initio calculated parameters of the crystal field acting on the ground J = 15/2 multiplet on the basis of the ab intio results presented in Table 1 (in units of cm−1). The parameters are given for the coordinate system employed in the ab initio calculations (given in the SI).

k q parameters of the crystal field 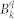Inline graphic
2 −2 −0.8223285E + 00
2 0 −0.2952967E + 01
2 2 0.2085183E + 01
4 −4 0.5765483E − 02
4 −2 −0.9592991E − 03
4 0 −0.4952142E − 02
4 2 −0.2436407E − 01
4 4 −0.3230413E − 01
6 −6 0.3422329E − 04
6 −4 0.1810159E − 04
6 −2 0.4855725E − 04
6 0 0.2270114E − 04
6 2 −0.1666892E − 04
6 4 0.6830792E − 04
6 6 −0.6617125E − 04
Open in a new tab

The ab initio calculated magnetic properties of DyNCN are in good agreement with direct current (dc) magnetic susceptibility measurements (Figure S7) which gives confidence in the anisotropic properties of the low-lying KDs discussed above. In addition, as shown in Figure S8, the preliminary powder INS spectra obtained on DyNCN exhibit two peaks, around 19 and 28 meV, that are also roughly consistent with the state transitions predicted by the ab initio calculation. Unfortunately the strong H background prevents a more detailed statement on the level structure and further investigations will be discussed in a separate publication.

Static magnetic properties

The investigation of the magnetic properties of a polycrystalline sample revealed a room temperature χMT value of 13.8 cm3 K mol−1 (Figure S7), in agreement with the expected value for g = 4/3 of the 6H15/2 ground state of a single DyIII. A gradual decrease on lowering the temperature is observed above 10 K and attributed to the depopulation of the substates. The lowest Kramers doublet has strong uniaxial magnetic anisotropy along the C2 axis. The next Kramers doublet lies at about 176 cm−1. The large energy difference results in a predominant population of the lowest levels up to relatively high temperature: the population ratio remains 99.3% at 50 K. Thus, the static magnetic behavior of the complex below 50 K is almost exclusively described by the ground doublet.

Dynamic magnetic properties

However, dynamic magnetic properties will be strongly influenced by the nature of excited substates. To investigate this possibility, variable-frequency alternating current (ac) magnetic susceptibility measurements were performed.

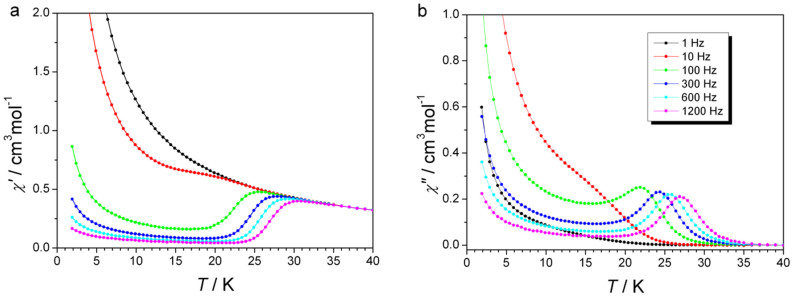
As the hallmark of a SMM, the in-phase (χ′) and out-of-phase (χ″) component, of DyNCN are characterized by the frequency dependence below ~35 K going through a frequency dependent maximum (>100 Hz) on lowering the temperature (Figure 4a, b), signaling the “freezing” of the spins by the anisotropy barrier arising from the split substates. To quantify the thermally activated process, the χ″ curves were divided by the dc susceptibility χdc, in which the relaxation time τ matches the inverse of the angular frequency 2πν exactly at the peak temperature of the corresponding curve (Figure S9)32,33. As expected for a single-molecule magnet, the relaxation times exhibit an exponential dependence on temperature between 24 and 27.5 K, and an Arrhenius fit to the data gives an effective relaxation barrier of Ueff = 233(4) cm−1, with a pre-exponential factor of τ0 = 6(1) × 10−10 s (Figure 5). The barrier height of DyNCN is more than 50 cm−1 above the first excited KD, which strongly supports the assignment that an Orbach process occurs through the second excited state (Figure 3 Bottom). This assignment is consistent with ab initio calculated energy of the second excited KD (266 cm−1 in the best approximation (see the ESI)), which fits perfectly the barrier Ueff = 270(5) cm−1 extracted for the diluted sample (Figure 5).

Figure 4. ac susceptibility.

Figure 4

Open in a new tab

Temperature dependence of the in-phase (χ′, a) and out-of-phase (χ″, b) components of the ac magnetic susceptibility for DyNCN under zero applied dc field.

Figure 5. Relaxation times.

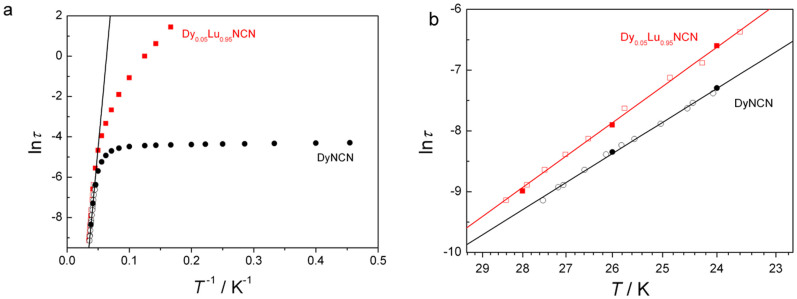
Figure 5

Open in a new tab

(a) Plot of inverse temperature versus the natural log of the relaxation time for DyNCN (black circle) and Dy0.05Lu0.95NCN (red square). In the higher temperature part shown as hollow symbols, relaxation times are extracted from χ″/χdc (T) diagrams (Figure S9); relaxation times represented by solid symbols are determined from χ″ (ν) diagrams (Figure S10). (b) Highlight of Arrhenius plots at high-temperature regime in Figure 5a. The solid lines correspond to a fit to the Arrhenius low for DyNCN and Dy0.05Lu0.95NCN, respectively, affording Ueff (DyNCN) = 233(4) cm−1 and Ueff (Dy0.05Lu0.95NCN) = 270(5) cm−1.

On cooling, deviations from the Arrhenius law become more and more important, which indicates that the blocking under this barrier is not complete and not even observable at all when T < 10 K with a temperature-independent relaxation time 10−4 s. The observed relaxation rate at this temeprature is entirely due to quantum tunneling of magnetization (QTM). In the undiluted sample of DyNCN the QTM is mainly due to the contribution of magnetic dipolar interactions to the transversal component of internal magnetic field Hdip at each Dy site. This leads to the tunneling splitting of the ground-state Kramers doublet by the amount Δtun = gX,YμBHdip, while this tunneling gap contributes directly to the QTM relaxation rate. Given the relatively large value of the latter (Figure 5a), magnetic hysteresis in this compound is only observed without coercivity using the sweep rate accessible with a conventional magnetometer (Figure 6).

Figure 6. Magnetic hysteresis.

Figure 6

Open in a new tab

Magnetic hysteresis at 1.9 K at a sweep rate accessible with a conventional magnetometer for DyNCN (grey) and Dy0.05Lu0.95NCN (red) with a clear opening of the hysteresis curves. Inset: A small coercive field of hysteresis observed in Dy0.05Lu0.95NCN.

In order to reduce the influence of the molecular surrounding on the spin dynamics of the dysprosium ion, magnetic measurements on a sample in which DyIII is magnetically diluted by the isostructural LuIII analogue in a molar ratio of 1:19 (Dy0.05Lu0.95NCN) were performed. In contrast to the pure DyNCN, hysteresis is observed with a small coercive field for the diluted sample (inset of Figure 6). As a result of reduction of thansversal component of internal field Hdip upon dilution, the relaxation times at low temperatures are two orders of magnitude slower than those operating in the undiluted sample. Therefore, as observed also in other crystals containing SMMs34, magnetic site dilution effectively chokes the pathway for ground state quantum tunneling. Here, the ac spectra could only be recorded only within a limited frequency range of 0.04 Hz, which prevented observation of the more sluggish real quantum regime at temperatures below 6 K.

Figure S11 shows that in the presence of an external dc field H the relaxation rate τ−1 increses in the pure DyNCN compound and decreases in the diluted Dy0.05Lu0.95NCN sample. The applied magnetic field is known to suppress the QTM and to enhance the direct relaxation process. We may conclude from Figure S11 that the variation of the two contributions do not cancel each other completely, so that the total relaxation rate increases in the former and decreases in the second compound with applied magnetic field.

Upon increasing the temperature to the thermally activated regime (23.6–28.4 K), the relaxation time is hardly affected by magnetic dilution, and from this we can extract the slightly larger energy barrier of Ueff = 270(5) cm−1 (τ0 = 1.3(3) × 10−10 s) which comes closer to the value expected from the height of the second excited Kramers doublet.

The relaxation via the second excited state in the compounds DyNCN and Dy0.05Lu0.95NCN (Figure 3 bottom), jointly confirmed by ac susceptibility and ab initio calculation, is remarkable and totally unprecedented since it originates from a C2 symmetry of the complex. Contrary to what is reported here, the relaxation via the second excited state, recently observed on some Dy sites of K2Dy4 and Dy5 complexes34, is achieved due to very strong Dy-O interaction with one of the oxygen ions and not due to symmetry reasons. Furthermore, the obtained results further allow us to support the use of the CASSCF/RASSI-SO method as a suitable tool for the determination of strength of Ln crystal field in lanthanide-based molecules, especially, to be able ultimately to elaborate the crystal field splitting for the systems with low symmetry coordination environments.

Conclusions

In summary, a new carbon coordinated dysprosium single ion magnet, DyNCN, in which the DyIII ion possesses an effective C2v crystal field symmetry has been investigated. The presence of the C2 symmetry axis requires that several low-lying KDs of the magnetic anisotropy axes coincide with it, as corroborated by ab initio calculations resulting in the two lowest Kramers doublets being strongly axial and possessing parallel anisotropy axes. This explains the observed thermally activated relaxation via the second excited KD. This new relaxation mechanism, offers a means to exploit single ion effects of lanthanide possessing perfect axial symmetry in order to facilitate magnetic relaxation climbing up to a higher energy levels, and to further open up a broader space for enhancing the anisotropy barrier. Furthermore, our findings should stimulate interest for the synthesis and characterization of organometallic lanthanide-based compounds.

Methods

Synthesis

The synthesis of the compound DyNCN and the Lu analogue are described in literature25.

Magnetic measurements

Magnetic susceptibility measurements were performed in the temperature range 2–300 K, using a Quantum Design MPMS XL-7 SQUID magnetometer equipped with a 7 T magnet. The dc measurements were collected from 2 to 300 K and the ac measurements were carried out in a 3.0 Oe ac field oscillating at various frequencies from 1 to 1500 Hz and with a zero dc field. The diamagnetic corrections for the compounds were estimated using Pascal's constants35, and magnetic data were corrected for diamagnetic contributions of the sample holder.

Inelastic neutron scattering

The neutron spectroscopy measurements were performed on the SEQUOIA spectrometer36,37 at the Spallation Neutron Source of Oak Ridge National Laboratory. The coarse resolution chopper was phased for and incident energy of 70 meV and spun at 240 Hz. A 1.71 g sample was sealed in an He atmosphere in a flat clan to fully cover the 5 cm × 5 cm beam. The sample was designed to minimize the amount of time needed to see a signal above the H background. The sample was cooled to ~5 K using a closed cycle He refrigerator. The raw time of flight data were converted to instrument independent units of Q and energy transfer and is normalized by V to remove detector efficiency differences.

Ab initio calculations

All ab initio calculations were performed with the Molcas 7.8 ab initio quantum chemistry program package38. All ab initio calculations were performed on the experimental X-ray structure, without employing optimization of the molecular structure by computational methods.

All elements were described using standard relativistic basis sets from the ANO-RCC library available in Molcas39. Several basis set models were employed in order to test the stability of the obtained solutions. Contractions of the employed basis sets for each atom for all computational models are given in the ESI. The results presented further in the main text correspond to the largest basis set model. In this model the Dy, Cl, N, O and C from the first coordination sphere were described by a QZP basis set, TZP quality basis sets were assigned for the atoms from the second coordination sphere, while the remaining atoms were described by DZP quality basis set. In order to save disk space, the Cholesky decomposition of bielectronic integrals was employed with a threshold of 0.5 × 10−7.

The spin eigenstates were calculated within the Complete Active Space Self-Consistent Field (CASSCF) method40. The active space of the CASSCF method included 9 electrons of DyIII spanning seven 4f-type orbitals. The [2,6-(2,6-C6H3R2N = CH)2-C6H3] carbanion is a closed shell molecule, and the HOMO does not enter into the active space. This was confirmed from test calculations on a smaller fragment (ESI) including the HOMO orbital of the carbanion into the active space which showed that this does not influence the overall results. The spin-orbit coupling was taken into account within the restricted active space state interaction (RASSI) method41, by mixing all 21 spin-sextet states (corresponding to the free ion multiplets 6H, 6F and 6P), 128 spin quartet states (4I, 4F, 4M, 4G, 4K, 4L, 4D, 4H, 4P 4G, 4F, and 4I), and 130 spin-doublet states (2L, 2K, 2P, 2N, 2F, 2M, 2H, 2D, 2G and 2O). On the basis of the resulting spin-orbital multiplets, the SINGLE_ANISO42 program was used to compute Zeeman splitting (g tensor) and static magnetic properties, molar magnetic susceptibilty and magnetization. Furthermore, a recent development allows, within the SINGLE_ANISO module, for a one-to-one mapping of the ab initio results onto the classical crystal field acting on the ground J = 15/2 multiplet. In other words, the reported crystal field parameters (Eq. 1) for the investigated DyNCN compound are obtained by a direct projection of the ab intio results and not by fitting.

The employed CF Hamiltonian is:

graphic file with name srep05471-m1.jpg

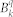where Inline graphic are the parameters describing the crystal field, while 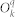Inline graphic are the Extended Stevens Operators43.

Furthermore, on the basis of the obtained results, the structure of the blocking barrier was analysed.

Author Contributions

J.T. designed and supervised the research. C.W. and D.C. carried out the synthesis and characterization studies. Y.-N.G. and J.T. planned and executed the magnetic measurements and analysed the resulting data. G.E.G. and S.E.N. performed the INS measurements. L.U. and L.F.C. performed the ab initio calculations and proposed the interpretation. Y.-N.G., J.T. and A.K.P. wrote the manuscript, with contributions from all the co-authors.

Supplementary Material

Supplementary Information
srep05471-s1.pdf (733.8KB, pdf)

Acknowledgments

This work was supported by the National Natural Science Foundation of China (21221061, 21301136, 21371166 and 21331003). Work at the ORNL Spallation Neutron Source is supported by the US Department of Energy Basic Energy Sciences Scientific User Facilities Division. L.U. is a postdoc of the FWO–Vlaanderen (Flemish Science Foundation). INPAC and Methusalem projects of the KU Leuven are also gratefully acknowledged. We also thank Dr. Yupeng Pan, Dr. Yang Wang and Dr. Wei Zhao for the help in preparation of sample and fruitful discussions.

References

  1. Gatteschi D., Sessoli R. & Villain J. Molecular Nanomagnets (Oxford University Press, 2006). [Google Scholar]
  2. Gatteschi D., Caneschi A., Pardi L. & Sessoli R. Large clusters of metal-ions - the transition from molecular to bulk magnets. Science 265, 1054–1058 (1994). [DOI] [PubMed] [Google Scholar]
  3. Sessoli R. et al. High-spin molecules: [Mn12O12(O2CR)16(H2O)4]. J. Am. Chem Soc. 115, 1804–1816 (1993). [Google Scholar]
  4. Leuenberger M. N. & Loss D. Quantum computing in molecular magnets. Nature 410, 789–793 (2001). [DOI] [PubMed] [Google Scholar]
  5. Hill S., Edwards R. S., Aliaga-Alcalde N. & Christou G. Quantum coherence in an exchange-coupled dimer of single-molecule magnets. Science 302, 1015–1018 (2003). [DOI] [PubMed] [Google Scholar]
  6. Bogani L. & Wernsdorfer W. Molecular spintronics using single-molecule magnets. Nat. Mater. 7, 179–186 (2008). [DOI] [PubMed] [Google Scholar]
  7. Urdampilleta M., Klyatskaya S., Cleuziou J. P., Ruben M. & Wernsdorfer W. Supramolecular spin valves. Nat. Mater. 10, 502–506 (2011). [DOI] [PubMed] [Google Scholar]
  8. Sessoli R. & Powell A. K. Strategies towards single molecule magnets based on lanthanide ions. Coord. Chem. Rev. 253, 2328–2341 (2009). [Google Scholar]
  9. Gatteschi D. Anisotropic dysprosium. Nat. Chem. 3, 830–830 (2011). [DOI] [PubMed] [Google Scholar]
  10. Guo Y.-N., Xu G.-F., Guo Y. & Tang J. Relaxation dynamics of dysprosium(III) single molecule magnets. Dalton Trans. 40, 9953–9963 (2011). [DOI] [PubMed] [Google Scholar]
  11. Blagg R. J., Muryn C. A., McInnes E. J. L., Tuna F. & Winpenny R. E. P. Single pyramid magnets: Dy5 pyramids with slow magnetic relaxation to 40 K. Angew. Chem. Int. Ed. 50, 6530–6533 (2011). [DOI] [PubMed] [Google Scholar]
  12. Chibotaru L. F., Ungur L. & Soncini A. The origin of nonmagnetic Kramers doublets in the ground state of dysprosium triangles: Evidence for a toroidal magnetic moment. Angew. Chem. Int. Ed. 47, 4126–4129 (2008). [DOI] [PubMed] [Google Scholar]
  13. Rinehart J. D., Fang M., Evans W. J. & Long J. R. Strong exchange and magnetic blocking in N23−-radical-bridged lanthanide complexes. Nat. Chem. 3, 538–542 (2011). [DOI] [PubMed] [Google Scholar]
  14. Woodruff D. N., Winpenny R. E. P. & Layfield R. A. Lanthanide Single-Molecule Magnets. Chem. Rev. 113, 5110–5148 (2013). [DOI] [PubMed] [Google Scholar]
  15. Cucinotta G. et al. Magnetic anisotropy in a dysprosium/DOTA single-molecule magnet: Beyond simple magneto-structural correlations. Angew. Chem. Int. Ed. 51, 1606–1610 (2012). [DOI] [PubMed] [Google Scholar]
  16. Lin P. H. et al. A polynuclear lanthanide single-molecule magnet with a record anisotropic barrier. Angew. Chem. Int. Ed. 48, 9489–9492 (2009). [DOI] [PubMed] [Google Scholar]
  17. Feltham H. L. C. et al. A non-sandwiched macrocyclic monolanthanide single-molecule magnet: The key role of axiality. Chem.-Eur. J. 17, 4362–4365 (2011). [DOI] [PubMed] [Google Scholar]
  18. Guo Y.-N. et al. Strong axiality and Ising exchange interaction suppress zero-field tunneling of magnetization of asymmetric Dy2 single-molecule magnet. J. Am. Chem Soc. 133, 11948–11951 (2011). [DOI] [PubMed] [Google Scholar]
  19. Lin P.-H. et al. A rare μ4-O centred Dy4 tetrahedron with coordination-induced local chirality and single-molecule magnet behaviour. Eur. J. Inorg. Chem. 1535–1539 (2011). [Google Scholar]
  20. Long J. et al. Single-molecule magnet behavior for an antiferromagnetically superexchange-coupled dinuclear dysprosium(III) complex. J. Am. Chem Soc. 133, 5319–5328 (2011). [DOI] [PubMed] [Google Scholar]
  21. Ungur L. & Chibotaru L. F. Magnetic anisotropy in the excited states of low symmetry lanthanide complexes. Phys. Chem. Chem. Phys. 13, 20086–20090 (2011). [DOI] [PubMed] [Google Scholar]
  22. Tuna F. et al. A high anisotropy barrier in a sulfur-bridged organodysprosium single-molecule magnet. Angew. Chem. Int. Ed. 51, 6976–6980 (2012). [DOI] [PubMed] [Google Scholar]
  23. Rinehart J. D. & Long J. R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2, 2078–2085 (2011). [Google Scholar]
  24. Gatteschi D. & Sessoli R. Quantum tunneling of magnetization and related phenomena in molecular materials. Angew. Chem. Int. Ed. 42, 268–297 (2003). [DOI] [PubMed] [Google Scholar]
  25. Gao W. & Cui D. Highly cis-1,4 selective polymerization of dienes with homogeneous Ziegler–Natta catalysts based on NCN-pincer rare earth metal dichloride precursors. J. Am. Chem Soc. 130, 4984–4991 (2008). [DOI] [PubMed] [Google Scholar]
  26. Jiang S.-D. et al. Series of lanthanide organometallic single-ion magnets. Inorg. Chem. 51, 3079–3087 (2012). [DOI] [PubMed] [Google Scholar]
  27. Jeletic M. et al. An organometallic sandwich lanthanide single-ion magnet with an unusual multiple relaxation mechanism. J. Am. Chem Soc. 133, 19286–19289 (2011). [DOI] [PubMed] [Google Scholar]
  28. Jiang S.-D., Wang B.-W., Sun H.-L., Wang Z.-M. & Gao S. An organometallic single-ion magnet. J. Am. Chem Soc. 133, 4730–4733 (2011). [DOI] [PubMed] [Google Scholar]
  29. Layfield R. A. et al. Influence of the N-bridging ligand on magnetic relaxation in an organometallic dysprosium single-molecule magnet. Chem.-Eur. J. 16, 4442–4446 (2010). [DOI] [PubMed] [Google Scholar]
  30. Sulway S. A., Layfield R. A., Tuna F., Wernsdorfer W. & Winpenny R. E. P. Single-molecule magnetism in cyclopentadienyl-dysprosium chlorides. Chem. Commun. 48, 1508–1510 (2012). [DOI] [PubMed] [Google Scholar]
  31. Ritter S. Single-molecule magnets evolve. Chem. Eng. News 89, 8–8 (2011). [Google Scholar]
  32. Ishikawa N., Sugita M., Ishikawa T., Koshihara S.-y. & Kaizu Y. Mononuclear lanthanide complexes with a long magnetization relaxation time at high temperatures: A new category of magnets at the single-molecular level. J. Phys. Chem. B 108, 11265–11271 (2004). [Google Scholar]
  33. Magnani N. et al. Magnetic memory effect in a transuranic mononuclear complex. Angew. Chem. Int. Ed. 50, 1696–1698 (2011). [DOI] [PubMed] [Google Scholar]
  34. Blagg R. J. et al. Magnetic relaxation pathways in lanthanide single-molecule magnets. Nat. Chem. 5, 673–678 (2013). [DOI] [PubMed] [Google Scholar]
  35. Theory and Applications of Molecular Paramagnetism. (Boudreaux, E. A. and Mulay, L. N. John Wiley & Sons, 1976). [Google Scholar]
  36. Granroth G. E., Vandergriff D. H. & Nagler S. E. SEQUOIA: A fine resolution chopper spectrometer at the SNS. Physica B 385–86, 1104–1106 (2006). [Google Scholar]
  37. Granroth G. E. et al. SEQUOIA: A newly operating chopper spectrometer at the SNS. J. Phys: Conf. Ser. 251, 012058 (2010). [Google Scholar]
  38. Aquilante F. et al. Software news and update MOLCAS 7: The next generation. J. Comput. Chem. 31, 224–247 (2010). [DOI] [PubMed] [Google Scholar]
  39. Roos B. O., Lindh R., Malmqvist P.-Å., Veryazov V. & Widmark P.-O. New relativistic ANO basis sets for transition metal atoms. J. Phys. Chem. A 109, 6575–6579 (2005). [DOI] [PubMed] [Google Scholar]
  40. Roos B. O., Taylor P. R. & Siegbahn P. E. M. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem, Phys. 48, 157–173 (1980). [Google Scholar]
  41. Roos B. O. & Malmqvist P. Å. Relativistic quantum chemistry: the multiconfigurational approach. Phys. Chem. Chem. Phys. 6, 2919–2927 (2004). [Google Scholar]
  42. Ungur L. & Chibotaru L. F. SINGLE_ANISO program in MOLCAS (http://molcas.org/documentation/manual/node95.html).
  43. Stevens K. W. H. Matrix Elements and Operator Equivalents Connected with the Magnetic Properties of Rare Earth Ions. Proc. Phys. Soc. A 65, 209 (1952). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep05471-s1.pdf (733.8KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES