Computational Delineation of Tyrosyl-Substrate Recognition and Catalytic Landscapes in the Epidermal Growth Factor Receptor Tyrosine Kinase Domain

Abstract

The epidermal growth factor receptor (EGFR) is a receptor tyrosine kinase (RTK), which catalyzes protein phosphorylation reactions by transferring the γ-phosphoryl group from an ATP molecule to the hydroxyl group of tyrosine residues in protein substrates. EGFR is an important drug target in the treatment of cancers and a better understanding of the receptor function is critical to discern cancer mechanisms. We employ a suite of molecular simulation methods to explore the mechanism for substrate recognition and to delineate the catalytic landscape of the phosphoryl transfer reaction. Based on our results, we propose that a highly conserved region, corresponding to Val852-Pro853-Ile854-Lys855-Trp856 in the EGFR tyrosine kinase domain (TKD) is essential for substrate binding. We also provide a possible explanation for the established experimental observation that protein tyrosine kinases (including EGFR) select substrates with a glutamic acid at the P−1 position and a large hydrophobic amino acid at the P+1 position. Furthermore, our mixed quantum mechanics/molecular mechanics (QM/MM) simulations show that the EGFR protein kinase favors the dissociative mechanism, although an alternative channel through the formation of an associative transition state is also possible. Our simulations establish some key molecular rules in operation for substrate-recognition and for phosphoryl transfer in the EGFR TKD.

Introduction

The epidermal growth factor receptor (EGFR) is one of the four members of the ErbB/HER family receptor tyrosine kinases (RTKs), which collectively regulate essential cellular functions, including proliferation, survival, migration and differentiation [1]. Each member of the ErbB family of RTKs is composed of an extracellular domain, a transmembrane segment, an intracellular protein tyrosine kinase domain, and a cytoplasmic tail (or C-terminal segment) harboring tyrosine phosphorylation sites. Under physiological conditions, ligand binding promotes homo- or heterodimerization of the receptors and activation of their cytoplasmic domains. Dimerization results in auto- or trans-phosphorylation of tyrosine residues in the RTK C-terminal segments, which serve as docking sites for signaling molecules containing SH2 or PTB domains [1]. Aberrant activation of the ErbB network due to the deregulation of the kinase domain (either due to over expression or due to mutations) is frequently associated with cellular transformation and clinical malignancies such as lung, gastric, and breast cancers. Hence, ErbB RTKs in general, and EGFR in particular have been identified as important drug targets in the treatment of cancer [2, 3]. Small molecule inhibitors of EGFR, namely, gefitinib, erlotinib, and lapatinib, are canonical examples of RTK inhibitors in targeted cancer therapy.

The deregulation of RTK signaling in human cancers can occur through several mechanisms: (1) increased ligand production through enhanced local autocrine activation; (2) specific gene translocations to produce kinase-domain fusions with altered signaling profiles; (3) RTK overexpression at the cell surface; (4) mutation of the RTK protein to modulate (enhance) activity; and (5) deregulation of phosphatase and endocytosis mechanisms to increase RTK signal propagation. The results form Catalog of Somatic Mutations In Cancer (COSMIC) has identified the prevalence of EGFR TKD mutations throughout many human cancers. In EGFR, the most common mutation is L858R, (sometimes also called L834R due to an alternate numbering convention which ignores the presence of a cleaved signal peptide). Even though this mutation accounts for over half of the mutations that are listed in COSMIC for EGFR in lung cancer, there are other mutations (DEL, S768I, L861Q, E709G, G719S, L833V, T790M) clinically related to enhanced drug-response [4–6]. However, it is rather striking to note that more than half of the residues in the kinase domain have been observed to be mutated in lung cancer samples; to be precise, 343 different mutations in 153 unique amino acid positions in the EGFR TKD has been clinically documented till date. Yet, only the eight mutations (L858R, DEL, S768I, L861Q, E709G, G719S, L833V, T790M) have been mechanistically studied for kinase activity or inhibition. Since the clinical data clearly indicate that the therapeutic response depends on the type of mutation, there is an imminent need to characterize the remaining mutations from a clinical perspective in order to determine the optimal treatment strategy for cancer patients harboring these other (i.e. outside of the eight) mutations. The recent availability of several crystal structures of the EGFR kinase domain [7–10] have brought to focus the importance of molecular details in the structure-function relationship, including the mechanisms for substrate recognition and phosphoryl transfer.

Tyrosine kinases catalyze protein phosphorylation reactions by transferring the γ-phosphate from an ATP molecule to the hydroxyl group of tyrosine residues in protein substrates [11]. Tyrosine kinase domains (TKDs) share a highly conserved two-lobed catalytic domain [11–13] implying a conserved catalytic mechanism [11–13]. The ATP binds into the cleft between the N- and the C- lobes and typically, two divalent metal (magnesium) ions are thought to be involved in the catalytic reaction [11, 12, 14, 15] along with a number of highly conserved regions in the catalytic domain, including the glycine-rich loop, the DFG motif of the activation loop as well as the catalytic loop. Collectively, they serve to position the phosphate of ATP and the two Mg²⁺ ions. Then, by recognizing [16, 17], recruiting, and phosphorylating a variety of peptide substrates, the kinase regulates several essential signaling pathways. Even though a complete elucidation of specificity in tyrosine phosphorylation by TKDs continues to be elusive [18], it is believed that the specificity of signaling cascades are in part determined by the sequence identity of phospho-tyrosines on substrates [19]. The specificity, in part, depends on how the kinase recognizes the local sequence of amino acids proximal to the binding site (shown in Figure 1) [20, 21]; the nomenclature for these resides are: P0 denotes the tyrosine, P−1, P−2, P−3, etc. are the amino acid labels in sequence going toward the N-terminus from the P0 site, and P+1, P+2, P+3, etc. are the amino acids in sequence going toward the C-terminus from the P0 site. It has been suggested that receptor tyrosine kinases including EGFR TKD show preference for substrates with glutamic acid at the P−1 position and large hydrophobic amino acids at the P+1 position [22–25]. The precise relationship of such a sequence identity to substrate specificity and the catalytic mechanism is still not understood.

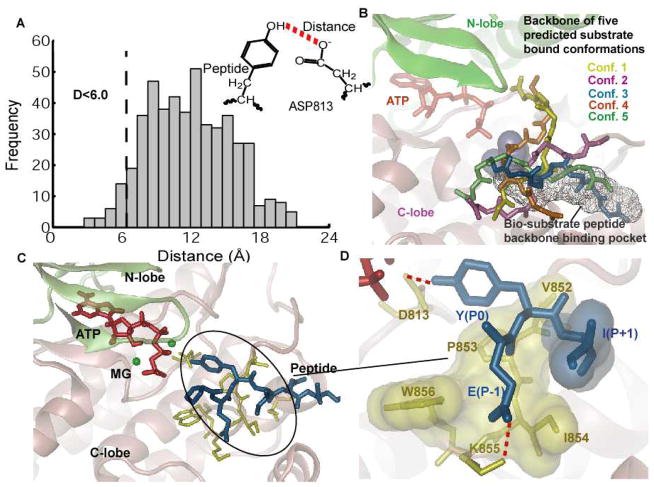
Figure 1.

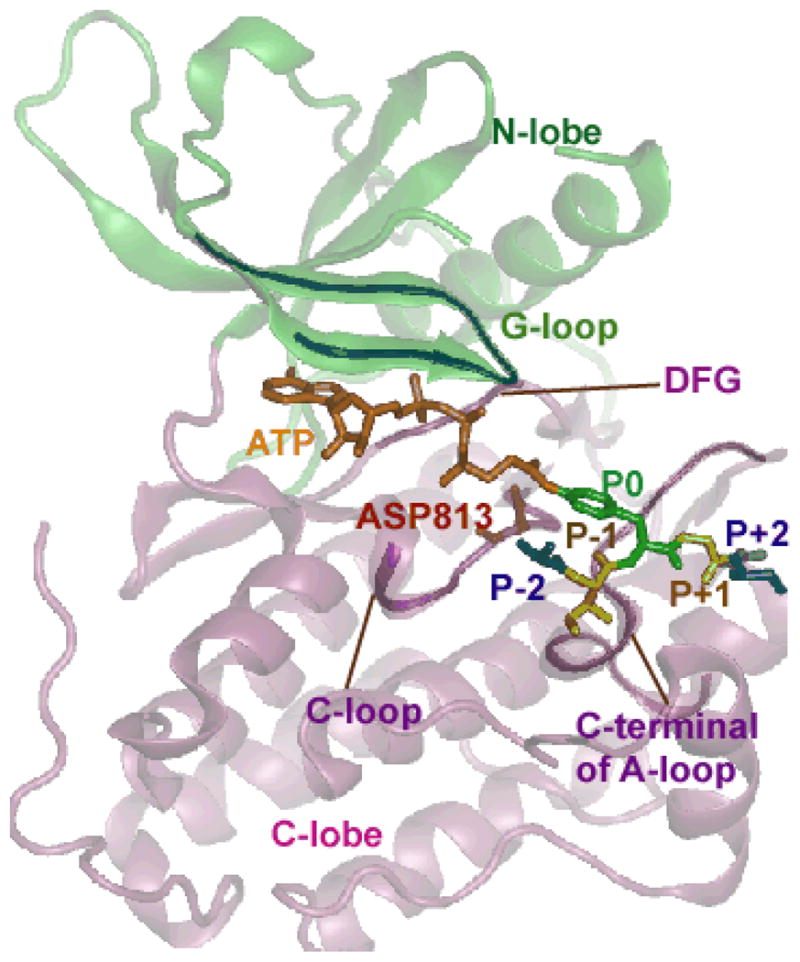
Structure of EGFR TKD co-crystallized with a bi-substrate analog. The kinase is depicted in ribbon representation, green color for N-lobe and pink color for C-lobe. The bisubstrate is represented as licorice with the color code as follows: ATP is shown in orange; tyrosine residue in the peptide is colored green and numbered as P0; the amino acids situated immediately proximal to the P0 site are numbered as P−1, P−2, P−3, etc., (going towards the N-terminus from the P0 amino acid), and P+1, P+2, P+3, etc., (going towards the C-terminus from the P0 amino acid), which are colored individually. The conserved aspartic acid residue (ASP813 in EGFR) is highlighted in red (stick representation). Other conserved motifs, namely the DFG motif, the C-loop, and the A-loop are also highlighted as opaque ribbons.

Experimental and theoretical studies have demonstrated that, in phosphoryl-transfer catalyzed by kinases and polymerases, the nucleophilic attack on the target phosphate proceeds via a conformation that resembles a trigonal-bipyramidal transition state [26, 27]. However, the phosphoryl-transfer itself can occur through either an associative or a dissociative mechanism [14, 26, 28, 29]. In the dissociative mechanism, the cleavage of the bond between the phosphorus center and the leaving group oxygen precedes the bond formation with the attacking nucleophile. On the contrary, in the associative mechanism, the bond formation between the attacking nucleophile and the phosphorus center precedes the bond cleavage. Although it is well accepted that the dissociative mechanism is the preferred mechanism for the reaction in solution for a monoester [30] (which is also the case most relevant for the reaction catalyzed by TKDs), discerning the transition state of protein kinase catalyzed reaction is complex, resulting in controversial experimental interpretations [14, 31–34]. Besides, it is also important to understand the catalytic roles of specific residues around catalytic site of a protein kinase, in particular, the role of the conserved aspartic acid residue (D813 in EGFR) in the catalytic loop [14, 35, 36]. To address this question in other well-characterized kinase systems such as PKA, CDK2, insulin kinase, and MAPK, computational methods have been successfully used to investigate the phosphoryl transfer reaction [28, 29, 37–42]. The challenge in extending such studies to EGFR kinase is that, while the structure for EGFR crystallized with a bi-substrate (ATP-peptide analog) is available [8], providing molecular resolution to the ternary complex of the kinase/substrate/ATP system, the covalent constraint between the ATP analog and the substrate, and the fact that the peptide sequence in the bi-substrate ligand is a c-Src substrate [8, 43] rather than a native EGFR substrate, introduces an important challenge in resolving the structural details of the catalytically productive ternary complex [44]. This brings to focus a related but equally important question on how EGFR kinase recognizes its native peptide substrates.

In this article, we employ methods of molecular modeling and simulation to: (1) investigate how the EGFR TKD recognizes the local amino acid sequence of substrates proximal to the binding site, and (2) characterize the EGFR TKD-catalyzed mechanism of phosphoryl transfer. Specifically, to address (1) we employ a computational protocol (see Figure 2) combining molecular dynamics simulations, ensemble molecular docking [45, 46], and Molecular Mechanics Poisson-Boltzmann Surface Area (MMPBSA) [47–53] to investigate the bound conformations of peptide substrates derived from two of the prominent autophosphorylation sites of the cytoplasmic tail region of the EGFR TKD [23], namely Y1068 (VPEYINQ) and Y1173 (NAEYLRV). We find that in our predicted bound conformations, the substrates bound into the same pocket as the bi-substrate peptide and that the P−1 glutamic acid residue and the hydrophobic amino acid at the P+1 position situate to interact with a highly conserved motif in the protein kinase family, namely Val852-Pro853-Ile854-Lys855-Trp856 in EGFR. This motif creates a binding surface to form hydrophobic contacts as well as hydrogen bonds to residues close to the tyrosine in the substrate and therefore helps to orient the tyrosine residue towards the active site. Using our predicted binary complex of EGFR TKD/substrate, we modeled the ternary complex structure of EGFR TKD/substrate/ATP and two Mg²⁺ ions, and addressed the phosphoryl transfer mechanisms in EGFR TKD using mixed quantum mechanics/molecular mechanics (QM/MM) simulations. Our QM/MM simulations showed that the EGFR protein kinase favors the dissociative mechanism, although an alternative channel through the formation of an associative transition state is also possible. Our potential energy scans suggested that the kinase directs the reaction through the dissociative channel primarily using a hydrogen bond between the conserved aspartic acid residue in the catalytic loop and the hydroxyl group of the substrate. The alternative channel can sustain weak activity, but can become significant in non-cognate environments where the catalytic aspartic acid is mutated or the enzyme is locked in a constitutively inactive conformation. Collectively, our simulations establish some key molecular mechanisms for the substrate binding and the phosphoryl transfer in the EGFR TKD.

Figure 2.

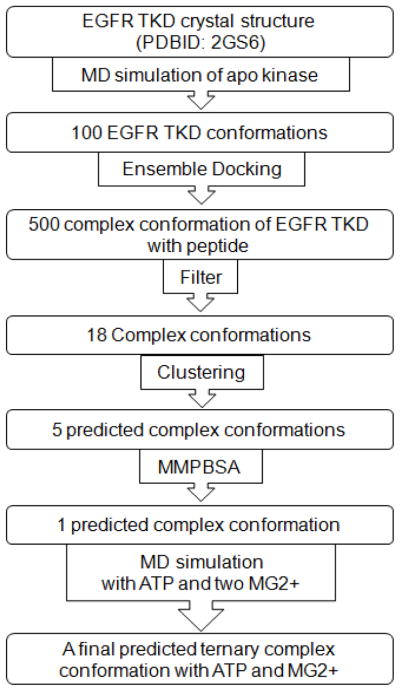
Docking protocol to predict peptide bound conformation in EGFR TKD.

Results

Tyrosyl-peptide substrate recognition by EGFR TKD

Following the computational protocols described in Figure 2 and the methods and materials section, 500 bound conformations were predicted using the ensemble docking protocol for binding of the EGFR TKD to a seven-residue native EGFR peptide with P0 corresponding to the autophosphorylation site Y1068 (VPEYINQ). Since a large number of the resulting structures showed peptide conformations in which the tyrosine residue was far from the active site, we constructed a histogram of D (the distance between the tyrosyl-oxygen and the Oδ₂ oxygen of the conserved catalytic aspartic acid residue D813, see Figure 3A), and only considered those conformations with D < 6 Å; this choice for the cut-off is intended to cover situations where the hydroxyl group of the peptide forms a hydrogen bond with Oδ₂ of D813, either directly, or through a water mediated interaction. As an additional filter, conformations where the peptide substrate overlaps with the position of ATP (quantified using the bi-substrate conformation in the PDBID:2GS6 structure) were also discarded. Thus, among the 500 predicted conformations, 18 structures of the TKD-substrate complex satisfied our constraints, which we categorized into 5 clusters based on root-mean-squared deviations (RMSD) of the backbone heavy atoms.

Figure 3.

Results for docking the peptide Y1068 to the EGFR TKD. A) Histogram of the distance between the oxygen in hydroxyl group of the tyrosine and the oxygen atom in the carboxylate group of the D813 for all the 500 predicted conformations by ensemble docking. Conformations with the above distance less than 6 Å were clustered into 5 clusters based on their backbone RMSD are shown in panel B. B) Five predicted peptide clusters of Y1068 bound conformations generated by ensemble docking that satisfied the distance criteria in panel A. The bi-substrate peptide binding pocket is also shown in the background, for reference. All 5 conformations were re-ranked using the MMPBSA method (see Table 1). C) Bound conformation of the peptide Y1068 to EGFR TKD in the presence of ATP and two MG²⁺ ions after 10 ns of MD simulation. The ATP atoms are depicted in red, MG²⁺ in green, peptide in blue, and residues in EGFR TKD that interact with the peptide in yellow. D) Depiction of the main interactions between the peptide and the kinase: Y(P0) hydrogen-bonds with D813; E(P−1) forms a salt bridge interaction with residue K855; the hydrophobic residue I(P+1) interacts with a hydrophobic surface in EGFR TKD consisting of the residues V852-P853-I854-W856. All hydrophobic residues are depicted as transparent surfaces.

The five conformations with the lowest score in each cluster are depicted in Figure 3B, along with the bi-substrate conformation from the PDBID:2GS6 structure. The computed MMPBSA binding free energies ΔGs (see methods and materials section) of the five conformations are provided in Table 1. As would be expected, the binding free energy is dominated by the difference between the unfavorable polar solvation and the favorable molecular mechanics terms. Interestingly, the conformation 3, which corresponds to the lowest MMPBSA score, also aligns the closest to the bi-substrate conformation as shown in Figure 3B and Table 1. A 9 ns MD simulation (see methods and materials section) performed using conformation 3 in the presence of ATP and two Mg²⁺ ions reached steady state after 3 ns of simulation (Figure 4). The peptide backbone is stable during the entire simulation as monitored by the backbone RMSD relative to the initial conformation (Figure 4). Therefore, our predicted substrate conformation emerges to be in close alignment with the bi-substrate structure in PDBID:2GS6 structure as shown in Figure 2B. The side-chain residues, however adjust conformations to result in stable hydrogen bonds and hydrophobic interactions in the final predicted bound structure of the ternary complex (EGFR TKD/tyrosyl-substrate/ATP) as shown in Figure 3C,D.

Table 1.

Rescoring of the top five predicted Y1068 peptide conformations predicted by ensemble docking using the MMPBSA method based on 1 ns MD simulation. The RMSD is calculated between the backbone atoms of the central five residues of the modeled peptide to the backbone atoms of the five-residue peptide portion of the bi-substrate in the structure 2GS6.

Conf.	ΔŪMM (Kcal/mol)	ΔW̄PB (Kcal/mol)	ΔW̄SA (Kcal/mol)	ΔḠtrans (− TΔS̄trans) (Kcal/mol)	ΔḠrot (− TΔS̄rot) Kcal/mol)	ΔḠtotal (Kcal/mol)	RMSD to bi-substrate (Å)
1	−157.4	153.3	−7.7	5.2	4.2	−2.4	5.45
2	−131.4	121.9	−7.5	5.5	4.3	−7.2	5.09
3	−134.4	109.4	−6.5	4.9	4.3	−22.2	2.72
4	−206.3	197.4	−7.9	5.4	4.2	−7.3	5.97
5	−107.5	103.7	−7.3	5.2	4.3	−1.6	3.92

Figure 4.

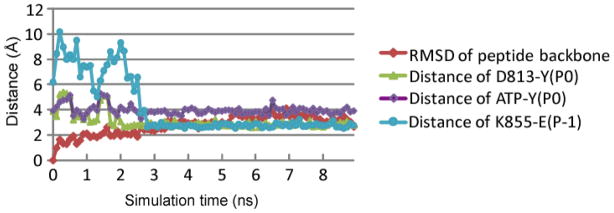
Evolution of the RMSD and key distances in the 10 ns MD simulation of EGFR TKD bound to ATP and the Y1068 peptide substrate. The color schemes are: the RMSD calculated based the backbone atoms of the central 5 residues of the peptide relative to the initial conformation (red); the distance between D813:Oδ₂ and Y(P0):Oη (green); the distance between Y(P0):Oη and ATP:P_γ (purple); and the salt bridge distance between K855 and E(p−1) (turquoise).

The predicted conformation (Figure 3C,D) provides new insights into the substrate recognition mechanism of EGFR TKD: (1) with respect to the P0 tyrosine, the C-terminus region of the peptide is anchored into a binding pocket formed by residues in the C-terminus region of the EGFR activation loop, and the N-terminus of the peptide extends to the front of the C-lobe of EGFR TKD (Figure 3C); (2) The hydroxyl oxygen of the P0 tyrosine is 2.9 Å away from the Oδ₂ oxygen atom of residue D813, i.e. within a hydrogen bonding distance (Figure 3D); (3) the P−1 glutamic acid residue forms a salt-bridge with a highly conserved lysine residue (K855); and (4) the isoleucine in the P+1 position situates in a hydrophobic pocket formed by Val852, Pro853, Ile854, and Trp856 (Figure 3D).

To further validate the robustness of this predicted mode of tyrosyl-substrate interaction, we also predicted the bound conformation of a different EGFR-native peptide sequence (NAEYLRV) derived from the auto-phosphorylation site Y1173 of EGFR. 500 bound conformations were predicted using the ensemble docking protocol for binding of EGFR TKD peptide Y1173. 22 structures of the TKD-substrate complex were found to satisfy our constraint of D < 6 Å, which we categorized into 6 clusters based on root-mean-squared deviations (RMSD) of the backbone heavy atoms, shown in Figure 5A. The computed MMPBSA binding free energies ΔGs of the six conformations are provided in Table 2. The conformation 5, which corresponds to the lowest MMPBSA score, also aligns the closest to the bi-substrate conformation as shown in Figure 5A and Table 2. A MD simulation performed using conformation 5 in the presence of ATP and two Mg²⁺ ions reached steady state, resulting in stable hydrogen bonds and hydrophobic interactions yielding a final predicted bound structure of the ternary complex of the EGFR TKD/tyrosyl-substrate/ATP. The conformation predicted for Y1173 is very similar to what we describe for Y1068 (shown in Figure 5, see also Table 2). In particular, the hydrogen bond between the hydroxyl of tyrosine and D813, the salt-bridge between E(P−1) and K855, and the hydrophobic contact between L(P+1) and VAL852-Pro853-Ile854 are all preserved. However, we note that the best MMPBSA score for the Y1173 peptide is lower than that for Y1068, implying that the binding affinity of the Y1173 peptide to the active state of the kinase is lower than that for the Y1068, as predicted by the calculations. This is consistent with the observations of Gibbes-Johnson et. al., who report that the experimental binding affinity of the Y1173 peptide is indeed lower than that of the Y1068 peptide in EGF-stimulated receptors [54]. Hence, while the salient features for peptide substrate recognition might involve just the P−1, P0, and P+1 sites, we note that interactions with more distal sites can be important in fine tuning the overall binding affinity of the peptide substrate to the kinase. Indeed, it has been experimentally known that a non-native substrate (called the optimal substrate in the literature) for EGFR TKD with sequence EEEYFEL has a binding affinity that is 8-fold stronger than that for the native Y1068 substrate [54].

Figure 5.

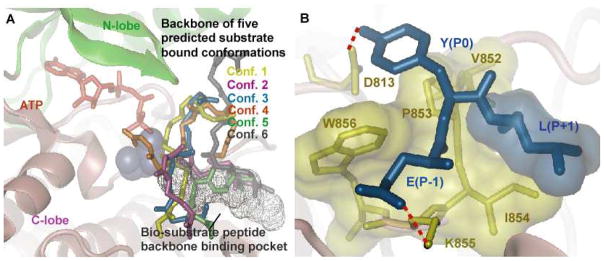
Results for docking the peptide Y1173 to EGFR TKD. A) Six predicted peptide clusters of the Y1173 bound conformations generated by ensemble docking that satisfied the distance criteria in panel A. The bi-substrate peptide binding pocket is shown in the background, for reference. All 6 conformations were re-ranked using the MMPBSA method (see Table 2). B) A depiction of the main interactions between the peptide and kinase: Y(P0) hydrogen-bonds with D813; E(P−1) forms a salt bridge interaction with residue K855; hydrophobic residue L(P+1) interacts with a hydrophobic surface in EGFR TKD consisting of residues V852-P853-I854-W856. All hydrophobic residues are depicted as transparent surfaces.

Table 2.

Rescoring of the top six predicted Y1173 peptide conformations predicted by ensemble docking using the MMPBSA method based on 1 ns MD simulation. The RMSD is calculated between the backbone atoms of the central five residues of the modeled peptide to the backbone atoms of the five-residue peptide portion of the bi-substrate in the structure 2GS6.

Conf.	ΔŪMM (Kcal/mol)	ΔW̄PB (Kcal/mol)	ΔW̄SA (Kcal/mol)	ΔḠtrans (− TΔS̄trans) (Kcal/mol)	ΔḠrot (− TΔS̄rot) Kcal/mol)	ΔḠtotal (Kcal/mol)	RMSD to bi-substrate (Å)
1	−436.5	394.6	−8.0	5.9	4.5	−39.4	9.6
2	−238.0	217.1	−6.9	4.7	4.3	−18.8	10.0
3	−243.8	226.2	−8.1	5.4	4.3	−16.1	7.9
4	−114.2	111.8	−7.4	5.1	3.9	−0.7	10.6
5	−297.0	241.3	−7.1	5.3	4.7	−52.8	3.6
6	−250.1	228.5	−8.0	5.4	4.3	−19.9	9.7

Pre-catalytic conformational landscape orchestrates multiple reaction channels

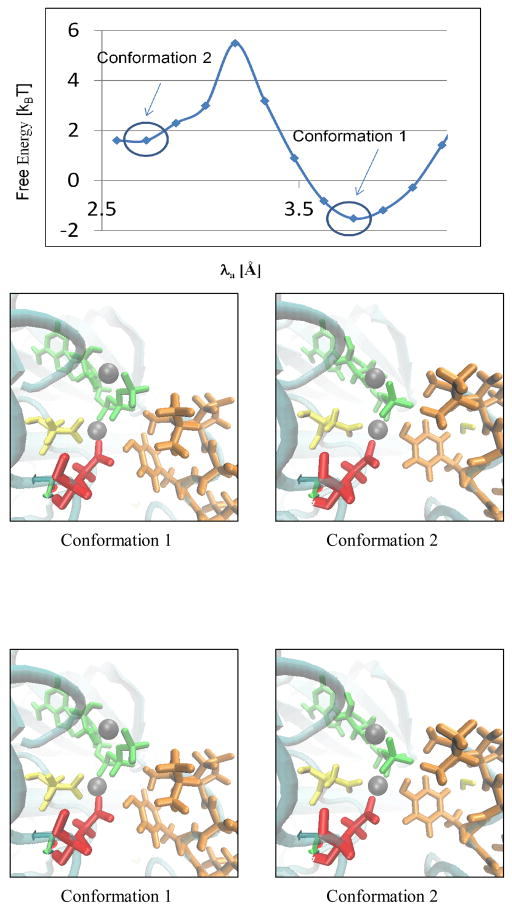
During the course of the MD simulation of the ternary complex involving the Y1068 peptide (Figure 4), the conformational equilibration of ATP and the two Mg²⁺ ions relative to the substrate tyrosine resulted in small rearrangements of the phosphate tail of ATP within the active site. Hence, we chose to explore the free energy landscape for the pre-organization of the nucleophilic attack distance λ_a (Y(P0):Oη - ATP:P_γ distance) as this distance is most relevant to catalysis as well as the most sensitive to the phosphate tail conformation, see Figure 6. Conformation 1 in the figure 6 is obtained from energy minimization of our model structure, λ_a ≈4 Ǻ. The system settles into another metastable state with λ_a <3 Ǻ (conformation 2 in figure 6), surpassing a nominal free energy barrier of 3.5 k_BT (2 Kcal/mol). This subtle pre-catalytic conformational transition corresponds to a conformational rearrangement of the γ-phosphate of ATP, see discussion below.

Figure 6.

Pre-Catalytic conformational landscape along the nucleophilic attack distance λ_a. Representative snapshots of conformations 1 and 2 are also depicted. In these snapshots the ATP is in green, the peptide is in orange, D813 is in red, D831 is in yellow, and the Mg²⁺ ions are in grey.

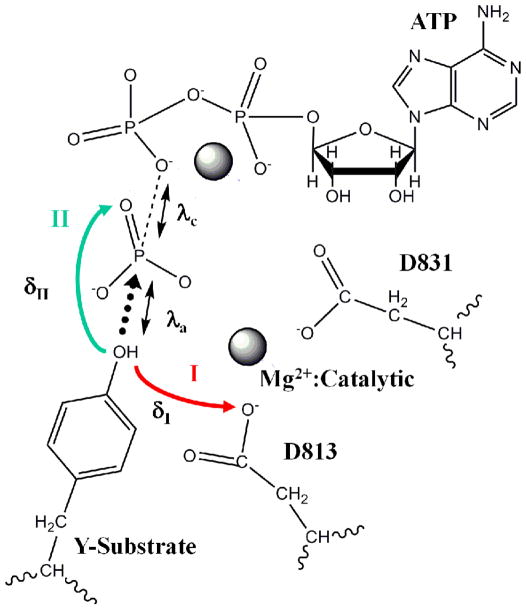
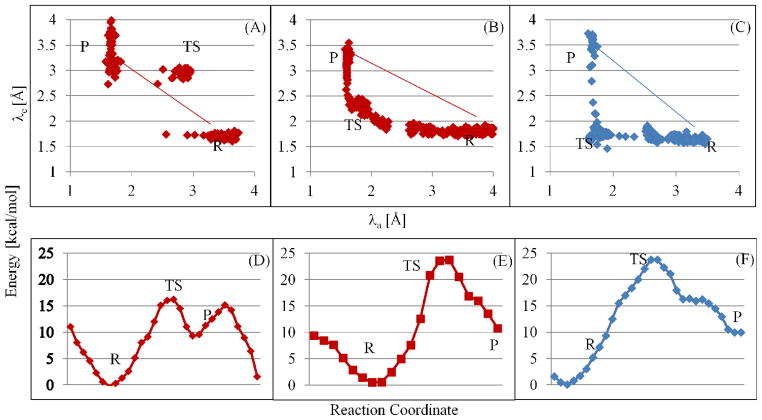
An analysis of the conformations within the window corresponding to conformation 2 revealed that that the proton of the tyrosine-hydroxyl (Hη) is primed for transfer to two possible positions owing to two mutually exclusive hydrogen bonds: (1) hydrogen bonded to Oδ₂ oxygen of D813 (indicated by a small value of δ_I), and (2) hydrogen bonded to the O1γ oxygen of ATP (indicated by a small value of δ_II), see Figure 7. We hypothesize that the bimodal distributions of δ_I and δ_II values represented in the normalized histograms in Figure 7A,B serve to select either of two competing catalytic routes, labeled as pathways I and II in Figure 8 for proton transfer and concomitant phosphoryl transfer. We explore this hypothesis further by investigating the possible mechanisms of phosphoryl transfer in EGFR TKD following the protocols for QM/MM minimization and QM/MM MD simulations (see methods and materials section). Our simulations (see Figure 9 and Figure 10) reveal that the phosphoryl transfer via pathway I, in which the proton is abstracted through the catalytic aspartic acid residue, (highlighted in red, see Figure 8), can occur via both the dissociative (see Figure 9A), and associative mechanisms (see Figure 9B), while pathway II (highlighted in turquoise, see Figure 8) supports only the associative mechanism (Figure 9C). In the dissociative reaction channel, the sum of the nucleophilic attack distance λ_a (between Y-OH and ATP Pγ) and the bond-cleavage distance λ_c (between ATP Pγ and ATP O2/3β) in the transition state is greater than the corresponding sum in the reactant and product states; this scenario is reflected in Figure 9A where the λ_a+λ_c values for transition state (TS) are greater than those for Reactant (R) or Product (P) states, i.e., the TS region lies above the line joining the R and P states in the λ_a versus λ_c plot. In contrast, a nucleophilic attack through an associative mechanism is evident in Figure 9B where the λ_a+λ_c values for TS are smaller than those for R or P, i.e., TS lies below the line joining the R and P in the λ_a versus λ_c plot. Pathway II is characterized by the migration of the proton from the hydroxyl group of the tyrosine substrate to the O1γ oxygen of ATP and the subsequent transfer of the proton to the O3β atom of ATP. The phosphoryl transfer takes place concomitant with the proton transfer steps but only through an associative mechanism, see Figure 9C; interestingly, for this channel, our attempts to drive the system through a dissociative mechanism yielded an associative mechanism with the O2β atom of ATP playing the surrogate (as the leaving group) to the O3β atom of ATP.

Figure 7.

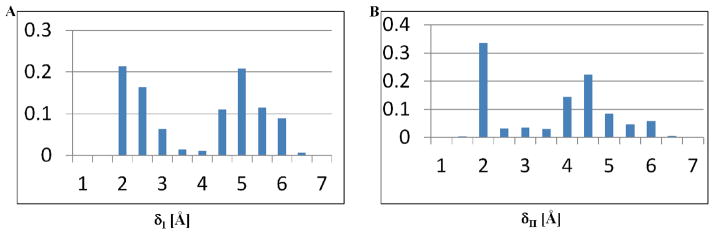
Normalized histograms representing the distributions of values for the distances between the proton of the substrate tyrosine hydroxyl and (A) the O2_δ oxygen of D813 in EGFR (δ_I); and (B) the O1_γ oxygen of ATP (δ_II) recorded in our simulations of the ground state (reactant) dynamics.

Figure 8.

Schematic of the proposed pathways for phosphoryl-transfer in EGFR TKD. Mg²⁺ ions and the catalytic aspartates (D831) are marked. Two pathways for proton migration (concomitant with phosphoryl-transfer) are shown. Pathway I (red) involves proton abstraction from the substrate tyrosine –OH group by D813 of EGFR, and pathway II (turquoise) involves proton migration to the O1_γ oxygen of ATP. δ_I and δ_II denote distances between the proton of the substrate tyrosine hydroxyl and either the O_δ2 oxygen of D813 (δ_I) or the O1_γ oxygen of ATP (δ_II). The nucleophilic attack distance, λ_a (distance between the tyrosine oxygen and the ATP P_γ) and the bond cleavage distance, λ_c (distance between the ATP P_γ and ATP O2/3_β) are also marked.

Figure 9.

QM/MM results for proposed pathways in figure 8 for the EGFR TKD/ATP/Y1068 peptide ternary complex. (A)&(D): Pathway I, dissociative mechanism; (B)&(E): Pathway I, associative mechanism; and (C)&(F): Pathway II, associative mechanism. R = reactant; P = product; and TS = transition state characterized by a trigonal bipyramidal geometry about P_γ. (A–C) Distributions of values for the nucleophilic attack distance, λ_a (distance between the tyrosine oxygen and the ATP P_γ) and the bond cleavage distance, λ_c (distance between the ATP P_γ and ATP O2/3_β) along the reaction pathways. (D–F) Energy changes along the reaction pathways in QM/MM simulations for the different mechanisms. In the energy landscape in panel D, the first peak corresponds to the formation of the trigonal-bipyramidal transition state where the proton from the tyrosine hydroxyl has been dissociated, while the second peak corresponds to the proton migrating to the ADP molecule.

Figure 10.

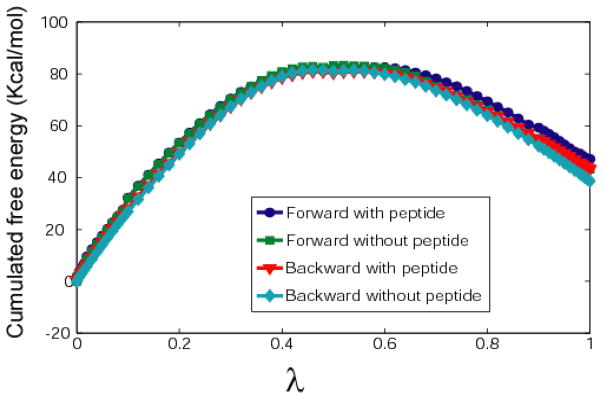
Cumulative free energy changes upon L834R mutation (Kcal/mol) calculated for bound and unbound Y1068 peptide substrates in both forward and backward directions in the free energy perturbation simulations.

Depictions of the snapshots highlighting key conformations of the active site along the reaction pathways are provided in a movie format in the accompanying supplementary material. In Figure 9(D–F), we depict the computed energy changes along the reaction pathways in active EGFR TKD, which suggest that for EGFR, the dissociative mechanism of phosphoryl transfer through pathway I corresponds to the lowest activation energy, E_a=16 kcal/mol (Figure 9D), while energy profiles for the associative mechanisms through pathways I and II yield barriers of 24 kcal/mol (Figure 9E) and 26 kcal/mol (Figure 9F), respectively.

Effect of mutation on tyrosyl-peptide substrate recognition

The kinase-activating mutation L834R locates closely to the catalytic site of EGFR TKD. To further investigate whether mutating a hydrophobic residue LEU to a positively charged residue ARG will affect the Y1068 peptide binding affinity, we employed the free energy perturbation (FEP) method to calculate the binding free energy difference between the wildtype and mutant systems. The FEP results (Figure 10 and Table 3) showed that L834R mutation resulted in a binding free energy change (ΔΔF) of 4.26 ± 0.32 Kcal/mol for the Y1068 peptide. Our results imply that the mutation does not increase (but rather decreases) the substrate binding affinity. Though experimental results probing the change in KM for the Y1068 peptide in L834R mutant and wildtype EGFR TKD systems are not directly available, Mulloy et al. has described the overall phosphorylation rate of Y1068 to increase modestly (fold increase in k_cat of 2.5 in EGF stimulated cells) [55]. This suggests that the mutation rather relies on a shift in the equilibrium between the inactive and active states of the kinase (by favoring the active state) for its activation mechanism.

Table 3.

Cumulative free energy change upon L834R mutation (Kcal/mol) calculated for bound and unbound Y1068 peptide substrate in both forward and backward directions.

	ΔF (Kcal/mol)		ΔΔF (Kcal/mol)
	With peptide	No peptide
Forward	47.188	43.247	3.941
Backward	43.3	38.716	4.584

Discussion and Conclusion

Crystal structures of multiple TKDs have already been solved, which has led to important insights in understanding the kinase function. However, most of these crystal structures are solved in the presence of ATP analogs and small molecule inhibitors. Due to the relatively low binding affinity of the interaction between TKD and peptide substrates, crystallization of TKD-peptide substrate complexes is still a challenge using experimental techniques. In this work, we suggest that a rich landscape exists for the binding of tyrosyl-substrate and subsequent pre-catalytic and catalytic events in the ternary complex of EGFR TKD/ATP/tyrosyl-substrate, from which we outline new molecular rules, which may, in part, contribute to specificity in phosphorylation reactions.

Our ensemble molecular docking protocol is successful in predicting bound conformations of a 7-residue peptide sequence derived from the cytoplasmic tail region of EGFR to EGFR TKD, with predicted bound conformation very similar to that found in a crystal structure of a bi-substrate analog co-crystalized with EGFR TKD [8] (PDBID: 2GS6). In our predicted complex, the aspartic residue D813 forms a hydrogen bond with the hydroxyl oxygen the P0 tyrosine of the peptide substrate. The aspartic residue has been shown to hydrogen bond with the hydroxyl group of serine/threonine/tyrosine in other kinase systems [34, 56, 57]. In the only existing EGFR TKD/bi-substrate analog structure (i.e. PDBID: 2GS6), the distance between the aniline nitrogen and the Oδ_1/2 oxygen of D813 is 6.37 Å, which makes it difficult to ascribe a role for the aspartic residue. The conformation in our modeled ternary complex clearly places the hydroxyl oxygen the P0 tyrosine 2.9 Å away from the Oδ₂ oxygen atom D813, i.e., within hydrogen bonding distance, which is consistent with the conceived role of D813 as a facilitator of proton abstraction.

Moreover, it has been suggested that protein tyrosine kinase (including EGFR) select substrates with glutamic acid at the P−1 position and large hydrophobic amino acids at the P+1 position [22–25, 58, 59]. Our predicted peptide bound ternary complex suggests that a highly conserved region, corresponding to Val852-Pro853-Ile854-Lys855-Trp856 in EGFR TKD is essential for substrate binding: Lys855 forms a salt bridge with the highly preferred glutamic acid residue at the P−1 site, and the hydrophobic pocket formed by Val852, Pro853, Ile854 and Trp856 serves to anchor a large hydrophobic residue at P+1 position. This observed binding mode for our top-ranked configuration is consistent with the hypothesis that the substrate-binding surface formed through hydrophobic contacts and hydrogen bonds help orient the tyrosine residue for catalysis [24]. Collectively, this extended region, i.e. Val852-Pro853-Ile854-Lys855-Trp856 in EGFR, has been identified as a highly conserved motif in the protein tyrosine kinase family [44], which further adds significance to our predicted conformation for the ternary complex. This allows us to conclude that a conserved binding surface on the kinase sandwiching the P0 tyrosine and making hydrophobic contact to the P+1 and hydrogen bond with P−1 residues, respectively, helps orient the tyrosine residue for catalysis [24]. Interestingly, the corresponding motif in serine/theronine kinase, with a sequence of Gly200-Thr201-Pro202-Glu203-Tyr204 in PKA, has been named as P+1 binding pocket and shown to be critical for substrate specificity [24, 60, 61]. In this case, the glutamic acid residue (E203) in this motif has been proposed to interact with preferred positively charged residues of the N-terminus site in PKA substrates [24] and residues Gly200, Pro 202, Thr201 and Tyr204 favor a hydrophobic residue in the P+1 position [21]. The similarity with the serine/threonine kinases raises the intriguing question as to whether an evolutionary path can be seen across species from a potential minimal and very inefficient transfer route to the much more efficient and Glu catalyzed route. This question may particularly be pertinent for the very unusual and highly conserved ability of MAP Kinasess to catalyze both, threonine and tyrosine phosphorylation.

Two of the main points of contention in kinase-catalyzed phosphoryl transfer reactions are whether the phosphoryl-transfer reaction occurs through an associative or a dissociative mechanism [14, 26, 28, 29] and whether the conserved aspartic (D813 in EGFR) functions as an acceptor for proton transfer from the hydroxyl group of the substrate. With the predicted peptide bound conformation, we were able to build the ternary structure of EGFR TKD, peptide with presence of ATP and Mg²⁺ ions and investigate the mechanistic details of EGFR TKD catalytic reaction mechanism using QM/MM simulations. Based on a pre-catalytic energy landscape of γ-phosphate of ATP we identify two alternative preferred proton positions of the tyrosine hydroxyl based on which we hypothesize two possible pathways: Pathway I involves proton abstraction from the substrate tyrosine hydroxyl group by D813 of EGFR, and pathway II involves proton migration to the O1_γ oxygen of ATP. Indeed, our QM/MM simulations support both pathways, with the phosphoryl transfer via pathway I sustained via both dissociative and associative mechanisms, while that via pathway II sustained by just the associative mechanism. The dissociative mechanism through pathway I has the most favorable energy barrier of 16 kcal/mol, while energy profiles for the associative mechanisms through pathways I and II each yield barriers of 24 kcal/mol. Combined with the pre-catalytic reaction energy barrier, our estimate for the net energy barrier ΔE_barrier for activation through the most favorable reaction channel (i.e. for pathway I through dissociative mechanism) in the active EGFR TKD is 16+2=18 kcal/mol. This value is compares favorably with the experimental value for the free energy barrier for EGF activated receptor system in the cellular context for which ΔG_barrier=k_BTln[k_BT/(k_cath)]=18.5 kcal/mol estimated from the reported k_cat of 17.4 min⁻¹ by Gibbes-Johnson et. al. [54]. Our estimate for the net energy barrier ΔE_barrier for activation through pathway II for active EGFR TKD is 24+2=26 kcal/mol. This translates to a k_cat of ≤10⁻⁶ s⁻¹ or a reduction by at least a factor 10⁻⁶ relative to the experimental k_cat of EGF activated receptor or a factor of 10⁻⁵ relative to experimental k_cat in the absence of EGF [62, 63]. The reduction in k_cat manifests itself as little or very weak residual activity through pathway II, which is consistent with recent experiments [64, 65].

Given that the protonation states of titratable side-chains in the active site can have considerable effect on the stability of the ground state as well as on the energies of the reaction landscape, we explored the different protonation states of the conserved catalytic residue D813 in EGFR. Multiple protonation states of the conserved catalytic residue (D831 of the DFG motif) were not considered because the location is relatively removed from the atoms involved in the catalytic reaction pathway. Although recent studies of the Abl kinase have reported that the protonation state of this residue is important in the flipping of the DFG motif toward the active conformation [66], such a flip for EGFR is already facilitated, even in the unprotonated state for D831, by kinase dimerization [67]. For the D813-protonated system, the phosphoryl transfer step occurs through an associative mechanism and proceeds with the simultaneous migration of the proton from the hydroxyl group of the tyrosine substrate to the Oδ₁ oxygen of D813 and the migration of Hδ₂ of the protonated Oδ₂ oxygen of D813 to O3γ atom of ATP (data not shown). Our attempts to drive the system through a dissociative mechanism yielded an associative mechanism with the O2β atom of ATP playing the surrogate (as the leaving group) to the O3β atom of ATP. These data imply that protonation of D813 is unlikely prior to the phosphoryl transfer.

ErbB3/HER3 is another member of the human epidermal growth factor receptor (EGFR/HER) or ErbB receptor tyrosine kinase family. ErbB3 is considered to be an inactive pseudokinase because it lacks several key conserved (and catalytically important) kinase domain residues – including the catalytic base aspartate. Indeed using QM/MM simulations we recently reported that phosphoryl-transfer can occur in an inactive conformation of ErbB3 TKD without abstraction of the tyrosine –OH proton by the catalytic base aspartate, which may explain the experimentally observed robust trans-autophosphorylation sustained in ErbB3, although this activity is substantially less than that observed in EGFR [68]. Pathway I is not sustainable in ErbB3 owing to the crucial substitution of Asn815 (analogous to Asp 813 in EGFR). However, like active EGFR TKD, the proton migrates to the O1_γ oxygen of ATP, through pathway II in Figure 8. Phosphoryl-transfer concomitant with this pathway can be catalyzed by ErbB3 in the inactive-like conformation, although it is predicted to be several orders of magnitude slower than the most favorable reaction channel in EGFR (i.e. for pathway I through a dissociative mechanism) – consistent with experimental observations. The finding also implies that this mechanism can operate in EGFR further suggesting that mutating D813 in this receptor may not completely abolish kinase activity. Indeed, a D813A-mutated variant of EGFR has been reported to retain its ability to promote EGF-dependent DNA synthesis and MAP kinase activation despite sustaining greatly reduced receptor autophosphorylation [69].

Members of the ErbB family of receptors — the epidermal growth factor receptor (EGFR/ErbB1/HER1), ErbB2 (HER2), ErbB3, and ErbB4 — activate a multi-layered signaling network mediating crucial pathways leading to cell proliferation and differentiation [1], in response to activation of the receptors by the epidermal growth factor (EGF), transforming growth factor-α, and several other related peptide growth factors [1]. Altered expression and mutations of ErbB receptors have been implicated in molecular mechanisms of oncogenesis, drug sensitivity, as well as resistance [67, 70–73]. In particular, altered or downstream signaling in cancer lines harboring ErbB mutations leading to preferential activation of certain downstream pathways over others have been discussed as the basis for the differences in cell phenotypic decisions in such cancer cells [74, 75]. While the molecular basis for such a selective activation of downstream pathways in still unclear, altered trafficking has been discussed as a possible mechanism leading to this state [76, 77]. The results we have presented in this article describe another possible mechanism that leads to preferential downstream signaling. Namely, the identity specific tyrosyl recognition (including the free energy landscape of pre-catalytic conformational rearrangements) at the catalytic site can be altered differentially by ErbB mutations, leading to differences in phospho-tyrosyl kinetics and adaptor binding downstream of receptor activation [67, 70–73]. The molecular mechanisms of tyrosine binding and the catalytic landscape of phosphoryl transfer discussed here, establish a direct link between receptor activation and downstream signaling. The results from our molecular model can help delineate mechanisms of preferential activation and help link them to drug sensitivity and resistance [78, 79].

Methods and Materials

We employ a suite of computational methods including molecular dynamics and molecular docking (see Figure 2), umbrella sampling, and QM/MM simulations to investigate molecular mechanisms of substrate recognition (i.e. bound conformation of a tyrosyl-peptide) by EGFR TKD and the catalytic mechanism associated with the subsequent phosphoryl transfer reaction.

Molecular dynamics (MD)

All the molecular dynamics simulations in this work were initiated by preparing the protein or protein complex structure by adding hydrogen atoms and missing residues using the CHARMM [80] biomolecular simulation package. The protonation states of histidine (HIS) residues were chosen according to recommendations from the WHATIF web interface (http://swift.cmbi.kun.nl/WIWWWI). Protonation states for all titratable groups distal to the catalytic site were chosen based on their individual pKa values in aqueous solution at a pH 7.0 [81]. The systems were then placed in a water (TIP3P model) box with 15Å padding. The ions were placed randomly to neutralize the systems using the Solvate and the Autoionize Plugins in the VMD package [82]. The systems were minimized for 50000 steps with heavy atoms fixed and further relaxed for another 50000 steps without any restraints. The systems were then gradually heated from 0K to 300K followed by 500 ps equilibrating runs at constant pressure (1 atm.) and temperature (300 K) to allow the system to reach the proper density. A productive trajectory was then generated at 300K and 1atm. The simulations were performed using NAMD with the CHARMM force field [83] with periodic boundaries enforced and long-range electrostatics taken into consideration.

Molecular docking

All the docking simulations in this work were performed with AUTODOCK 3.05 [84]. Grid maps were constructed as 126×126×126 points with a grid spacing of 0.184 Å to cover a pre-defined binding pocket. The Lamarckian Genetic Algorithm (LGA) [84] was applied to explore the conformational space of the substrate. In each docking run, the initial population was set to 100 individuals, the maximum number of energy evaluations was set to 10⁸, and the generation of GA run was set to 30,000.

Docking of substrate tyrosyl-peptides Y1068 and Y1173 to EGFR TKD

The active conformation of the wildtype EGFR TKD domain was modeled based on the 2GS6 structure from the Protein Data Bank [8]. A 10 ns dynamics trajectory was generated by molecular dynamics simulation using NAMD (see above) [85] and an ensemble of 100 protein conformations was derived by sampling at uniform intervals from the trajectory. Two 7-residue peptides derived from the cytoplasmic tail region of EGFR (corresponding to Y1068: namely, VPEYINQ and to Y1173: namely, NAEYLRV) were docked to each snapshot in the 100-member ensemble by molecular docking using Autodock 3.05 (see above) [84]. 5 possible bound conformations were predicted for each protein conformation, which in total yielded 500 bound conformations of tyrosyl-peptide/EGFR TKD for each peptide.

In order to further sort the binding conformations generated by the ensemble docking protocol, we employed Molecular Mechanics Possion Boltzmann Surface Area (MMPBSA) [48–53, 86] to calculate the binding free energy. For each of the predicted bound conformations, a 1 ns trajectory was generated using molecular dynamics. The MMPBSA energy of each modeled complex was calculated as the average of the single point MMPBSA scores of 500 snapshots derived from the 1 ns simulation; the water molecules and mobile ions were removed before the MMPBSA score calculation. In the MMPBSA calculation, the molecular mechanics energy, U_MM, was evaluated using an infinite cutoff for non-bonded interactions. The electrostatics contribution to the solvation free energy, W_PB, was calcuated with Poisson-Boltzmann solver in CHARMM [87]. The reference system was assigned a dielectric constant of 1 and 0 M salt concentration and the solvated system was assigned a dielectric constant of 80.0 and 100 mM salt concentration. The nonpolar contribution to the solvation free energy, W_SA, was approximated with the suface area model ΔW_SA=[0.00542 kcal/mol/Ų]×SASA +0.92 kcal/mol [88], where the molecular surface area (SA) was estimated with a 1.4 Å slovent probe radius. The translational and rotional entropy loss upon binding was estimated based on the fluctuations of the center of mass and that of orientations (Euler angles), by following the procedure described by Swanson et. al. [49]. Other (vibrational) entropy changes were neglected in this work.

The top ranked conformation of peptide Y1068 with EGFR TKD identified based on the MMPBSA score (Table 1) was chosen as the initial bound structure for further analysis of the catalytic mechanism. The ATP was placed in homology with the bi-substrate structure (PDB ID: 2GS6) [8] and two Mg²⁺ ions were placed in homology with those resolved in the crystal structure of PKA (PDB ID:1ATP) [37]. A 10 ns molecular dynamics simulation was performed on the ternary complex of ATP/substrate-Y/EGFR TKD.

Free energy perturbation (FEP)

To calculate the binding affinity change of EGFR TKD and its peptide upon the clinical mutation L834R, we designed a thermodynamic cycle shown in Figure 11. Based on this cycle, the binding free energy change ΔΔG_W→M is related to the free energy changes of the mutation in the bound state (ΔG_B) and the unbound state (ΔG_U):

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{W\to M}=\mathrm{\Delta }{G}_M-\mathrm{\Delta }{G}_W=\mathrm{\Delta }{G}_U-\mathrm{\Delta }{G}_B$$

Figure 11.

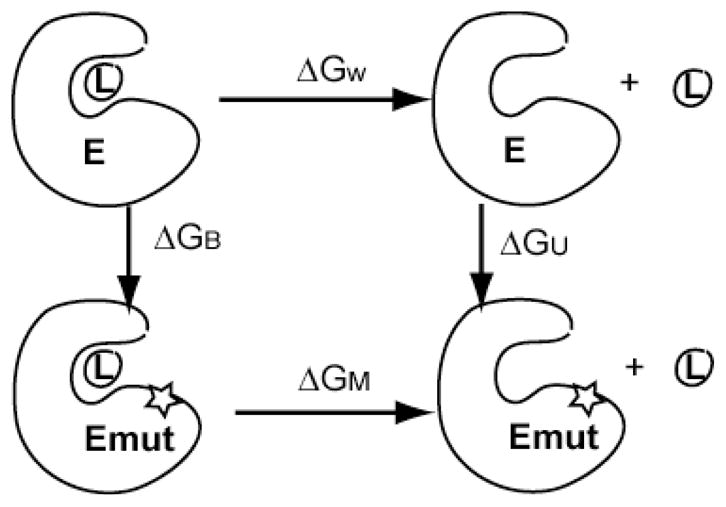
Thermodynamic cycle for the calculation of binding affinity change of ligand/substrate due to a mutation employed in the FEP simulations.

The free energy changes due to the particular mutation in the bound state (ΔG_B) and the unbound state (ΔG_U) were calculated by using the free energy perturbation (FEP) method. The free energy procedure was performed using the alchemical FEP method in NAMD 2.7b2 with the dual-topology construction. For each state (bound or unbound), we performed FEP calculations in both the forward and backward directions to ensure convergence, and to estimate the error. For each direction, the perturbation was divided into 72 windows (λ= 0, 10⁻⁶, 10⁻⁵, 10⁻⁴, 10⁻³, 10⁻², 0.005, 0.01, 0.015, 0.02, 0.03 to 0.1 with an interval of 0.01, 0.1 to 0.9 with a interval of 0.02, 0.9 to 0.98 with an interval of 0.01, 0.098, 0.0985, 0.099, 0.995, 0.999, 0.9999, 0.99999, 0.999999, 1). In each window, the system was equilibrated for 20 ps and run for another 100 ps for data collection. Larger window sizes and longer simulations have also been tested and the current setup gives us a reasonable convergence in the final binding affinity. To avoid the “end-point catastrophes”, the soft-core potential was used to gradually scale the unbounded interaction potential. The van der Waals and electrostatic interactions were scaled separately; that is, the vdW interactions were linearly coupled to the simulation from λ=0 (fully decoupled) to λ=1 (fully coupled) and the electrostatic interactions were coupled into the simulations over the range of λ=0.5 to λ=1. (For the vanishing particles, the vdW interactions were linearly decoupled from the simulation over the value range of 0 to 1, and the electrostatic interactions were decreased gradually from λ=0 to λ=0.5).

Sampling the pre-catalytic free energy landscape

Since the positions and orientations of the ions and ATP relative to the substrate tyrosines in our initial modeled structures were determined either from a bisubstrate ligand complex or by homology with protein kinase A (see above), prior to QM/MM simulations, we explored the classical free energy landscape along an a priori-chosen reaction coordinate χ₁ (the tyrosyl O-ATP P_γ nucleophilic attack distance). For computing the free energy landscape, the probability distribution P(χ₁) is calculated by dividing χ₁ into several (6–7) windows. The histograms for each window were collected by harvesting classical molecular dynamics trajectories of length 200 ps per window using a harmonic restraint 0.5×K×(χ₁-χ₁^i,0)², χ₁^i,0 being the pre-set of the reaction coordinate characterizing the i^th sampling window, and K=20 kcal/mol/Ų being the force constant for the restraint along χ₁. The sampling data from the different windows were then processed using the weighted histogram analysis method (WHAM) [89].

Quantum mechanics molecular mechanics (QMMM) simulations

The QM/MM approach we adopted was based on an existing interface between GAMESS-UK [90] and CHARMM [80]. For the quantum region, we chose the two Mg²⁺ ions, water molecules within 5 Å of the Mg²⁺ ions, segments of the ATP, the tyrosine residue of the substrate, and two catalytic residues (D813 and D831), yielding a total of 60 atoms. In order to reliably handle the phosphorous chemistry, the quantum region was treated using density functional theory with a B3LYP exchange correlation functional and a 6-31G* basis set [91], and the remaining protein and solvent molecules were treated classically using the CHARMM27 force field. Since the QM/MM boundary cuts across covalent bonds, we applied the single link atom procedure [92] to satisfy the valences of broken bonds in the QM region. The electrostatic interactions between the quantum region and the classical atoms belonging to groups at the QM/MM boundary were discarded as this choice has been shown to enhance the accuracy in the resulting energies and geometries [93]. We have extensively explored this choice of the QM/MM region (including sensitivity to the size of the QM region, and the functional/basis set combination) in our prior studies of closely related systems [94–96]; others have validated the choice of the link atom [93]. Non-bonded van der Waals (VDW) interactions were treated by applying a switching function at 10 Å and truncating the VDW potential energy smoothly at a cutoff distance of 12 Å. The forces in the quantum region were calculated on-the-fly, assuming that the system moves on the Born-Oppenheimer surface defined by the QM/MM Hamiltonian. The system was first subjected to 1200 steps of the adopted basis Newton-Raphson (ABNR) minimization and subsequently QM/MM MD simulations were performed during which the systems were first heated to 300 K and then subjected to constant temperature of 300 K dynamics using a Langevin thermostat for 10 ps using a standard 1 fs time step of integration.

Catalytic reaction pathways

The exact reaction coordinate is complex and multi (high) dimensional and a quantitative estimate of the free energy landscape cost can only be obtained using efficient long-time sampling approaches [97–101], which remain prohibitively expensive for QM/MM applications due to large computational cost. Although we believe that the true reaction coordinate is complex, in the spirit of the a recent study [102], we described the reaction pathways in terms of several simple reaction coordinates, χ. For mechanisms of phosphoryl transfer through associative mechanism, χ includes the reactive distance tyrosine O- ATP P_γ, tyrosine O- ATP O2/3β, and ATP P_γ- ATP O2/3β distances. For mechanisms of phosphoryl transfer through dissociative mechanism, in addition to the three distances, χ includes the coordinate for proton abstraction, namely tyrosine OH- D830:Oδ₂. In order to drive the system along a reaction coordinate, we performed restrained minimization as well as restrained sampling simulations using the QMMM Hamiltonian along χ by augmenting the Hamiltonian with a potential bias term (1/2)×K×(|χ|-χ₀)²; here K is the effective spring constant (ranging between 10 and 30 kcal/mol/Ų) and χ₀ are reference values for sampling in different windows of χ. Complete pathways were assembled by varying the offset distances χ₀ in increments of ±0.05 Ǻ, where the positive and negative increments represent the directionality of the energy scan. The reaction paths were computed by energy-minimizations in the presence of restraints and recalculating the single-point energies in the absence of the constraints. For our choice of the increments of χ₀, calculations performed in forward and reverse directions satisfied path reversibility in configurations as well as energy values. Following the energy scans, constant temperature restrained dynamics runs of 300 fs-1ps for each choice of χ₀ was also performed to ensure that the reaction path was robust to thermal fluctuations.

Abbreviations

MD

Molecular Dynamics

QM/MM

Quantum Mechanics/Molecular Mechanics

MMPBSA

Molecular Mechanics Poisson Boltzmann Surface Area

TKD

Tyrosine Kinase Domain

RTK

Receptor Tyrosine Kinase

EGFR

epidermal growth factor receptor

RMSD

root-mean-squared deviation

FEP

free energy perturbation

MMPBSA

molecular mechanics Poisson Boltzmann surface area