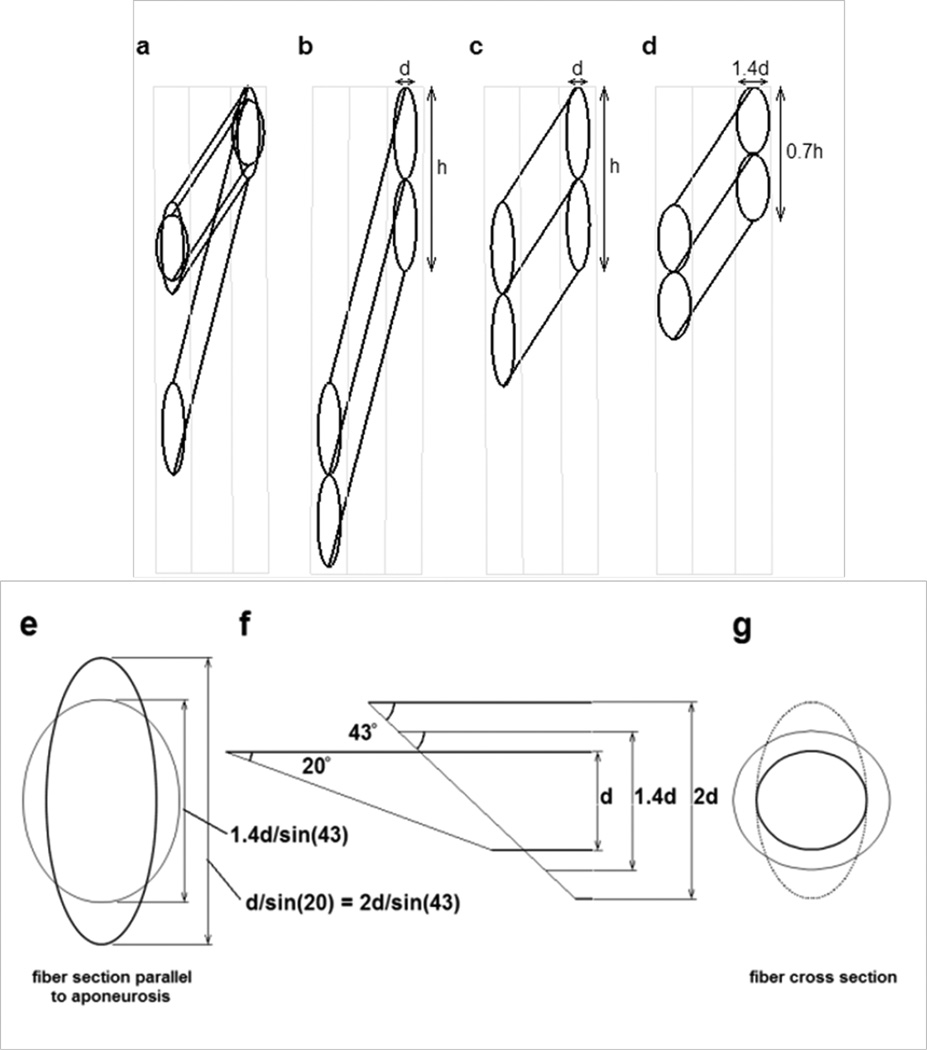
Fig. 13.

Diagrams illustrating possible geometry changes in muscle fibers as a pinnate muscle shortens. a) The possible changes in a muscle fiber with a circular cross section as it rotates between the aponeuroses and shortens to 50% of its original length. Two final configurations are shown, each maintaining the same volume during shortening. (i.e. As the muscle fiber length halves, the fiber cross sectional area must double). The resting pennation angle was 20° and the pennation angle after shortening was ~43°. b) Two resting fibers of diameter d between two aponeuroses at the pennation angle of 20°. The vertical distance (labeled as h for the pair of fibers) occupied by individual fibers on the aponeurosis is d/sin(20) or ~ 2.9d. c) The shortened fibers under the constraint that the aponeurosis separation remains constant and the aponeurosis length change is negligible. Distances d and h remain constant. d) The geometry change when the muscle fiber diameter increases symmetrically. As the fiber cross sectional area doubles, the fiber diameter must increase to ~1.4d. The vertical contact distance of the fiber on the aponeurosis would be 1.4d/sin(43°), or ~2.1d. e) The hypothetical contact area of the muscle fiber onto the aponeurosis. The taller ellipse shows the contact surface of the resting fiber at an angle of 20° to the aponeurosis and also of the contracted fiber illustrated in panel c. The shorter ellipse shows the contact area of the shortened fiber in panel d. f) The geometry between a fiber and the aponeurosis. The oblique end of the fiber represents the contact area with the aponeurosis, at an angle of 20° to the fiber for the resting fiber and 43° for the shortened fiber. The thinnest fiber, height d represents the resting fiber illustrated in panel b. The intermediate fiber, height 1.4d represents the geometry of a shortened fiber in panel d. The thickest fiber, height 2d represents the geometry of the shortened fiber in panel c. Note that the length of the oblique lines across the thinnest and the thickest fiber are equal although the overall muscle geometry has changes significantly. g) The changes in fiber cross section (perpendicular to the long axis of the fiber) showing the original fiber cross section (smallest circle) corresponding to panel b, the elliptical cross section of the fiber in panel c and the larger circular cross section of the fiber in panel d.