Essential Parameters for Structural Analysis and Dereplication by ¹H NMR Spectroscopy

Abstract

The present study demonstrates the importance of adequate precision when reporting the δ and J parameters of frequency domain ¹H NMR (HNMR) data. Using a variety of structural classes (terpenoids, phenolics, alkaloids) from different taxa (plants, cyanobacteria), this study develops rationales that explain the importance of enhanced precision in NMR spectroscopic analysis and rationalizes the need for reporting Δδ and ΔJ values at the 0.1–1 ppb and 10 mHz level, respectively. Spectral simulations paired with iteration are shown to be essential tools for complete spectral interpretation, adequate precision, and unambiguous HNMR-driven dereplication and metabolomic analysis. The broader applicability of the recommendation relates to the physicochemical properties of hydrogen (¹H) and its ubiquity in organic molecules, making HNMR spectra an integral component of structure elucidation and verification. Regardless of origin or molecular weight, the HNMR spectrum of a compound can be very complex and encode a wealth of structural information that is often obscured by limited spectral dispersion and the occurrence of higher order effects. This altogether limits spectral interpretation, confines decoding of the underlying spin parameters, and explains the major challenge associated with the translation of HNMR spectra into tabulated information. On the other hand, the reproducibility of the spectral data set of any (new) chemical entity is essential for its structure elucidation and subsequent dereplication. Handling and documenting HNMR data with adequate precision is critical for establishing unequivocal links between chemical structure, analytical data, metabolomes, and biological activity. Using the full potential of HNMR spectra will facilitate the general reproducibility for future studies of bioactive chemicals, especially of compounds obtained from the diversity of terrestrial and marine organisms.

Structure elucidation and identification of organic chemicals from natural and/or synthetic sources depends heavily on nuclear magnetic resonance (NMR) spectroscopy and mass spectrometry (MS) as complementary tools. Accordingly, contemporary laboratory procedures and journal guidelines require, at a minimum, the acquisition of a high-resolution 1D ¹H NMR (HNMR) spectrum as part of the structural dossier of any chemical entity. This applies to the structure elucidation component of scientific publications as well as structure proof documents in industrial settings. In practice, the acquisition of an HNMR spectrum is the first step in NMR-based structure elucidation and metabolomic analysis. Especially for sample-limited natural products, 1D ¹H NMR and its 2D counterparts are typically the first-line structural tools employed for identification and dereplication purposes. Reasons for placing emphasis on ¹H NMR-based analyses are its ability to accommodate submilligram and even submicrogram samples when coupled with cryoprobe technology, the wealth of structural information contained in the HNMR spectra, the compound specific characteristics of the resonances, and the resulting versatility of HNMR as a dereplication tool when combined with MS. The present study demonstrates that δ and J values of HNMR data should be routinely reported with 0.1–1 ppb and 10 mHz precision, respectively, in order to represent any (new) chemical entity adequately and enable subsequent dereplication of the compounds based on widely available HNMR spectra.

Representation of Frequency Domain HNMR Data

The HNMR analytical process of converting a frequency domain spectrum into an interpreted and tabulated summary of information requires a substantial amount of human intervention. This graphical-to-alphanumerical conversion occurs after the standard Fourier transformation and postacquisition processing of raw time domain NMR data (FID) into an actual frequency domain spectrum; a well-established process.^1,2 The interpreted results are generally summarized in the form of numerical listings or tables of chemical shift (δ [ppm]) assignments and J-coupling [Hz] information.

Most HNMR spectra, notably those of many “simple” small molecules, exhibit numerous convoluted signals. The wealth of structural information encoded especially in the rather complex signal patterns has been recognized in much earlier NMR studies.³ Regardless of the complexity of HNMR spectra, their interpretation has two main goals. The primary one is to provide substantiation of structure by demonstrating full consistency between the observed HNMR data and any proposed chemical structure(s), typically in conjunction with evidence from ¹³C NMR, 2D homo- and heteronuclear NMR, and MS data. No less important, the second goal is to enable others to reproduce the NMR data by appropriately documenting the necessary NMR spectral parameters required for structure dereplication. Optimizing dereplication via improved reproducibility of NMR data not only impacts the characterization of new or known natural products. On a broader scale, it also augments the ability of others to repeat reported isolation or synthetic schemes as well as metabolomic analyses. It also helps chemists to target the synthesis of the actual compound of interest, which has been identified as an important challenge at the interface of natural products discovery and synthesis of analogues.⁴

Constructing (digital) repositories of the actual NMR spectra, in both time and frequency domain, from documented (tabulated) NMR data represents a highly useful and arguably necessary tool for facilitating structural dereplication. However, in current practice, the standard operating procedure continues to consist primarily of converting the graphical HNMR spectra to an alphanumerical table. Recently, this approach has been extended by adding graphical representations of the spectra of new compounds to the primary literature, typically as part of Supporting Information. Despite this progress in documentation, the requirement to use identical spectrometer frequencies for direct graphical comparison represents an inherent drawback of this approach. Owing to the elimination of coupling information in ¹H-BB decoupled spectra, this limitation does not apply to ¹³C NMR-based methodology^5,6 for the validation of structures⁷ and recognition of incorrect structures of organic molecules, a topic that has recently received increasing attention. The results from the case studies presented here support the conclusion that HNMR might be a method that is equal to, or possibly even better than,⁸¹³C NMR to serve this purpose, provided that the HNMR data are properly analyzed and the reporting precision is adequate.

Aim

The principal purpose of the present study is to describe the conditions for which tabulated sets of spectral parameters (“HNMR data”) are able to substitute for the actual HNMR spectrum and how this data can adequately support accurate structural dereplication and specificity. The underlying hypothesis is that comprehensive interpretation of HNMR spectra requires an increased precision to 0.1–1 ppb (0.0001–0.001 ppm) and 10 mHz (0.01 Hz) for Δδ and ΔJ, respectively, to yield NMR parameter sets that are suitable as numerical substitutes for the actual spectra.

Approach

In order to demonstrate the validity of the overall approach, representative case studies were performed with chosen examples from a wide range of natural products classes: uzarigenin-3-sulfate (1) and progesterone (2) as steroid derivatives, syringetin (3) as a flavonoid glucoside, agnuside (4) as a monoterpenoid/iridoid glucoside, isoxanthohumol (5) as a hemiterpene flavanone hybrid, quinic acid (6) as a shikimate, and ambiguine N isonitrile (7) as a representative of the indole alkaloids. The molecules investigated are classic representatives of their structural class. For example, the spectra of the mono- and dicinnamoyl derivatives of 6 that occur commonly in plants are considerably more complex than that of 6. Similar considerations apply to the steroid glycosides, e.g., cardenolide dideoxy-glycosides as congeners of 1 and plant pregnanes and steroid saponins related to 2, as well as to other more complex terpenoids such as the triterpenoids and their glycosides. Similar considerations apply to the other compound classes; the complexity of organic molecules from nature provides ample complexity for future studies. In contrast to the plant-derived compounds, 1–6, ambiguine N isonitrile (7) is produced by the cyanobacterium Fischerella ambigua. It is a representative of the growing class of hapalindole-type alkaloids.

Further perspectives for the importance of adequate precision in HNMR data reporting are provided by reported case studies of molecules that have been subjected previously to full spin analysis, recently referred to as HiFSA (¹H iterative full spin analysis):⁹ the monoterpene β-pinene,¹⁰ the sesquiterpenoid perezone and its analogues,¹¹ the diterpenoid ent-3β-hydroxytrachylobane,¹² a series of diterpenoid lactones (ginkgolides) and flavonoids from Ginkgo biloba L.,^13,14 several alkaloids such as huperzine A,¹⁵ indole derivatives,¹⁶ anatabine¹⁷ analogues from Nicotiana species, tropane derivatives,¹⁸ flavonoids¹⁹ and flavonolignans, and dimeric phenylpropanoids ([iso]silybins) from Silybum marianum (L.) Gaertn.,²⁰ as well as mono- and oligosaccharides.²¹

In order to determine the critical parameters needed for HNMR spectral analysis and dereplication studies, the present work examines a total of 10 cases, discussing several aspects of the analyses with regard to the interpretation of signal patterns, the importance of frequently unrecognized phenomena such as virtual and heteronuclear couplings, and the overall impact on precision and accuracy of reported HNMR data. In order to provide a solid basis for studying the impact of small differences in the (reported) δ and J-coupling patterns of the molecules, the case studies are built on comprehensive analyses and full assignments of all HNMR spectra. This work was performed using the PERCH software tool and resulted in HiFSA fingerprints and profiles that are highly compound specific.⁹ Notably, HiFSA methodology can be readily interfaced with quantitative HNMR applications (HiFSA-based qHNMR).^14,20,22,23 HiFSA is a quantum mechanical spectral analysis (QMSA)²⁴ method that enables the comprehensive spin analysis (SA) of NMR spectra.²⁵

Chart 1.

Case Studies

Adequate Precision Is Essential for HNMR Spectral Analysis

Considering the persistent two-decimal standard for reporting chemical shifts (see also discussion on accuracy below), the maximum deviation between the actual and reported values are presumably not greater than ±0.005 ppm. However, even this precision level cannot be achieved without the help of computational tools and certainly not by visual inspection of 1D HNMR spectra. This particularly applies to spin-particles with intrinsic resonance overlap and/or higher order effects, such as ¹H.

The following case studies provide evidence as to why adequate precision is an essential requirement for HNMR spectral analysis and demonstrate how this approach enables structural dereplication based on tabulated HNMR data. For this purpose, it will be shown that even very small deviations (<0.01 ppm) between actual and reported chemical shifts can heavily influence the shape of “multiplets” and challenge subsequent attempts for definite structure dereplication. A systematic comparison of spectra calculated from actual δ values retrieved by accurate spin analysis (HiFAS)⁹ with spectra calculated using rounded values with “artificial” two-decimal precision is also discussed (up to 0.01 ppm, i.e., double the rounding up/down error, as spins are paired). While each of the case studies contributes its own specific aspects, all are considered in the subsequent sections, where recommendations are derived and the need for enhanced HNMR spectral interpretation and documentation is discussed from a dereplication perspective.

Case Study 1: Uzarigenin-3-sulfate (1)

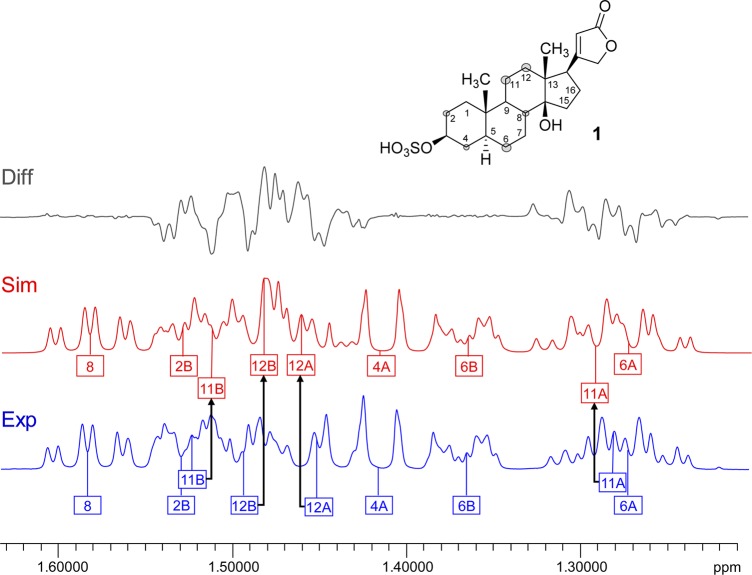
This steroid derivative contains 28 ¹H spin-particles, of which 23 appear in the relatively narrow window between 0.8 and 2.2 ppm. The challenge of describing this spin system results from the severe overlap of the HNMR resonances, which complicates the analysis and the extraction of accurate δ and J values much more than the presence of non-first-order effects. As such, 1 can be viewed as a representative case of the large class of steroids, showing the characteristic wider δ dispersion of the methylene and methine “envelope” in 5α steroids.^26,27 Figure 1 shows a section of the “fingerprint” region from 1.2 to 1.6 ppm with resonances for nine spin-particles (H-2b, H-4a, H-6a/b, H-8, H-11a/b, and H-12a/b) and compares the experimental spectrum with the calculated spectrum using chemical shifts for H-11a/b and H-12a/b rounded to the nearest 0.01 ppm, while retaining exactly identical J-couplings and line-shape parameters. The difference spectrum visualizes the apparent differences in the fingerprints that would be generated by truncating the δ values to two decimals. In contrast, precise reporting of the δ/J matrices allows the unambiguous dereplication of steroids with proton fingerprints similar or analogous to 1 to the level of their full relative configuration (S1, Supporting Information).

Figure 1.

Case study 1: uzarigenin-3-sulfate (1). Representing the class of steroidal natural products, 1 belongs to the 5α series and, thus, is a case of rather disperse δ distribution of the steroidal envelope. Given are the experimental spectrum (Exp, in blue) with accurate assignments of the nine protons in the region, compared with the simulated spectrum with chemical shifts rounded to 0.01 ppm for the methylene protons, H-11A/B and H-12A/B only (Sim, in red). The difference spectrum (Diff, in gray) clarifies the considerable deviations caused by the inappropriate rounding of δ values to two decimals, which translates into a visual mismatch of the “fingerprint” region of steroid HNMR spectra and can invalidate dereplication of these stereochemically demanding natural products (600 MHz, methanol-d₄).

The results for 1 apply to all steroids and, at least in general, to all other terpenoids (mono-, sesqui, di-, tri-) with alicyclic ring systems. Considering the existence of subtle stereochemical differences between the same type of terpenoids across major taxa (e.g., diterpenoids from plants vs bryophytes¹²), it is crucial to document the underlying NMR spectroscopic details. As recently shown for progesterone,^9,28 extraction of full δ/J parameter sets may require ultra-high-field NMR in combination with HiFSA. The availability of HiFSA profiles of steroidal portal structures and the development of comprehensive knowledge about their δ/J data characteristics will facilitate subsequent analysis of congeneric molecules at commonly available field strengths.

Case Study 2: Progesterone (2)

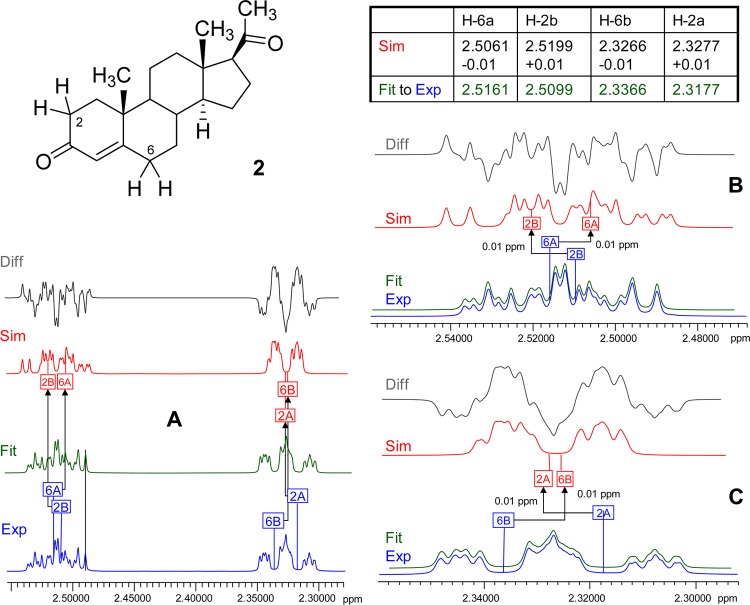
The availability of ultra-high-field NMR instrumentation (800–1000 MHz ¹H) has recently allowed for unprecedented chemical shift dispersion, not only in biomolecular but also in small-molecule NMR analysis. Expanding on the previous case study, the steroid 2 was chosen as a follow-up example of an alicyclic small molecule (314.5 amu) in which the methylene and methine envelope resonate in a more confined chemical shift window. Even at 900 MHz, the HNMR spectrum of 2 shows severe signal overlap in addition to higher order effects, requiring computational analysis (HiFSA) for complete extraction of accurate δ and J values. Traditional reporting of ¹H chemical shifts, with only two decimal places, originates from the early years of NMR, when the field strengths were much lower (<100 MHz for ¹H) and 0.01 ppm uncertainty meant variations of <1.0 Hz, which was typically less than the achievable line widths. However, at 900 MHz an uncertainty of 0.01 ppm translates into 9 Hz, which is the magnitude of a large J-coupling.

Figure 2 shows a “minimal worst case” scenario, where the chemical shifts of 2 are reported with a 0.01 ppm rounding deviation for only two pairs of protons, H-2A/B and H-6A/B, which are not coupled to each other. In this scenario, the chemical shifts of the diastereotopic methylene protons are reversed, resulting in completely different shapes of the (simulated) resonances. Importantly, such a reporting artifact prevents the iterative fitting process from converging unless additional permutation algorithms are applied or human intervention resolves the misalignment. While the complete spectral analysis for 2 has recently been published by our group,⁹ the analysis was repeated during the present study (S2, Supporting Information) and yielded consistent results within 0.000 05 ppm deviation for the extracted chemical shifts as well as 0.027 Hz for the J-couplings with respect to the root-mean-square (RMS) values of their residuals.

Figure 2.

Case study 2: progesterone (2). Even at ultrahigh magnetic field, the steroid 2, like many alicyclic terpenoids, exhibits overlapping resonances. HiFSA can produce complete δ/J profiles and fully fitted spectra (Fit, in green). As shown for the overlapping resonances of the two notably uncoupled methylene proton pairs, H-2a/b and H-6a/b (overview A, expansions B and C), reporting with only 0.01 ppm precision produces marked deviations in the resulting simulated spectra (Sim, in red), which in the case of H-2b and H-6a even results in a reversal of chemical shift order and misassignment of the signals (900 MHz, methanol-d₄). The difference spectra (Diff, in gray) show the extent of the mismatch produced by such inadequate reporting artifacts.

Case Study 3: Syringetin-3-O-β-d-glucoside (3)

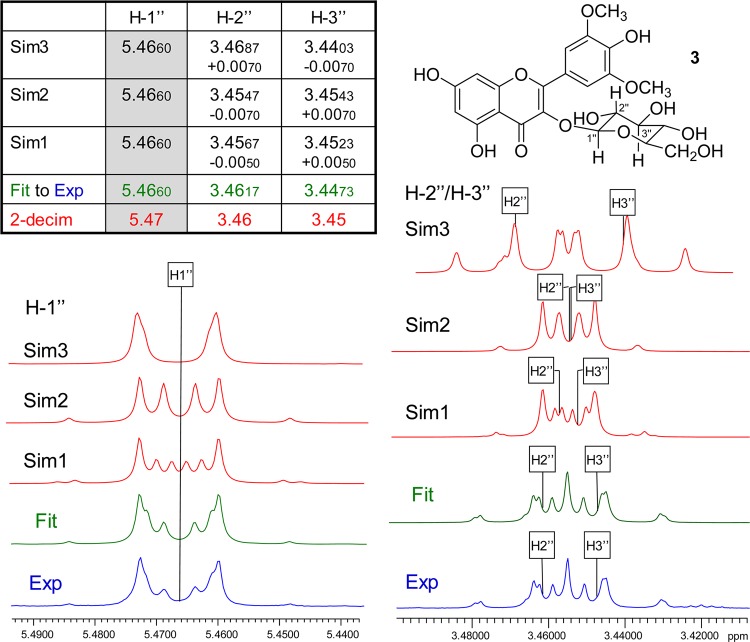
The sugar moiety of 3 is a typical example of a non-first-order spin system (Figure 3). The HNMR signal of the anomeric proton, H-1″, in the β-glucose moiety is subject to a pronounced higher order effect, which can potentially be misinterpreted as a (virtual) coupling. The deviation from its expected doublet (∼7.7 Hz) character results from the close resonance proximity between its directly coupled neighbor, H-2″, and the subsequently coupled vicinal neighbor, H-3″, which shows a difference in the chemical shifts (Δδ) of only 0.0144 ppm or 8.65 Hz at 600 MHz. The neighbor (α) and subsequent neighbor (β) protons of H-1″, H-2″, and H-3″, respectively, are also strongly coupled and heavily overlapped, as shown in Figure 3, which altogether explains the higher order effect. Quantum mechanical simulations (Sim1–3, Figure 3) with constant J-couplings show that even very small changes in the chemical shifts of H-2″ and H-3″ affect the appearance of the anomeric signal (H-1″). While the Δδ for H-2″ and H-3″ between Sim1 and Sim2 is only 0.002 ppm, which is equivalent to 1.2 Hz at 600 MHz, this small difference still has a remarkable effect on the appearance of the anomeric proton signal. Changes in the J-couplings between H-1″, H-2″, and H-3″ affect the appearance of all these complex “multiplets” and, together with δ rounding and/or reporting artifacts, can produce virtually any variation in the resulting signals, none of which will fit the actual experimental spectrum. In fact, 3 is a case where highly accurate reproduction of the observed spectrum requires δ reporting with four decimal point precision in order to reproduce the spectrum unambiguously for structure dereplication (S3, Supporting Information).

Figure 3.

Case study 3: syringetin-3-O-β-d-glucoside (3). Quantum mechanical simulation of the spin systems (scenarios Sim1–3, in red) shows that minor variations of the chemical shifts of the three protons H-1″, H-2″, and H-3″ of the glucose moiety lead to major deviations from the fitted spectrum (Fit, in green; matching the experimental data, Exp, in blue). All J values were kept constant for the simulations (600 MHz, methanol-d₄).

Case Study 4: Agnuside (4)

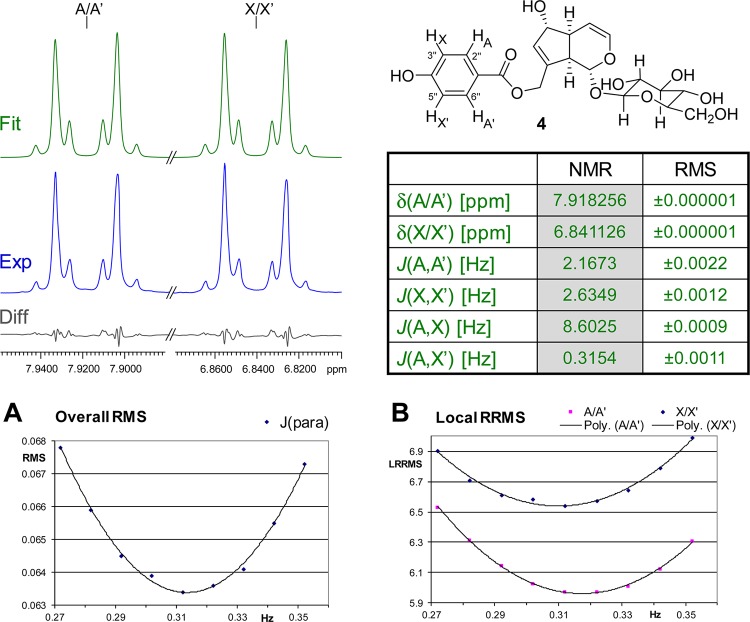
This case extends the previous case from the perspective of spin simulation. In fact, both cases exemplify the need for spectral simulation as an essential tool for HNMR spectral interpretation. Compound 4 represents a rather simple case of a higher order spin system, which is amenable to analysis with both basic simulation tools and more advanced approaches such as HiFSA (S4, Supporting Information). The four aromatic protons of the p-hydroxybenzoate moiety in 4 constitute an AA′XX′ spin system of a para-substituted benzene ring and produce a complicated pair of signals (Figure 4), which can be confused with (pseudo-) doublets or doublets of triplets, and frequently are labeled as “multiplets”. Interpretation of these resonances and extraction of the underlying J values cannot be achieved with first-order approximation (“visual interpretation”), but requires the use of spin simulation tools. The present study used the HiFSA approach⁹ to achieve a full analysis of the underlying spin system. While the proton pairs A and A′ as well as X and X′ consist of isochronous nuclei, the characteristic shape of their resonances is caused by the fact that the individual AA′ and XX′ protons are magnetically nonequivalent; that is, each of them has a different set of coupling relationships (e.g., H-A has ³J with H-X, ⁴J with H-A′, and ⁵J with H-X′, while H-A′ has ³J with H-X′, ⁴J with H-A, and ⁵J with H-X). Figure 4 shows the result of HiFSA for this spin system. Notably, fitting the system without this higher symmetry as an ABXY gives the same result: the fitted Δδ within the AB and XY pairs is below 0.0001 ppm (i.e., AB = AA′ and XY = XX′), and the corresponding couplings are the same to the second decimal place. This allows the conclusion that the chiral induction by the iridoid aglycone and the sugar moiety is too weak, due to the relatively large distance, and/or that rotation of the ester bond is fast relative to the NMR time scale. Together with the dynamic rotation of the B-ring, this induction is insufficient to produce chemical shift dispersion for the AA′ pair to become an AB pattern. Depending on their substitution, analogous aromatic partial structures could also produce AA′MM′ or AA′BB′ spin systems, which create even more complicated pairs of “multiplet” signals.

Figure 4.

Case study 4: agnuside (4). The complex aromatic resonances of the widely occurring para-substituted phenyl structural motif result from the underlying AA′XX′ (in 2), AA′MM′, or AA′BB′ (in analogous molecules) spin systems. Their precise numerical description was performed using the HiFSA approach⁹ and requires δ and J reporting precision to the low ppb and mHz levels, respectively. Shown on the top left are the experimental (Exp, in blue) and HiFSA fitted (Fit, in green) spectra, their residual difference (Diff, in gray), and the tabulated spin parameters and RMS values of the fit (360 MHz, methanol-d₄). Panel A: Plot of the overall residual RMS for different J values for the para-coupling ⁵J_A,X′. Panel B: Plot of the local RRMSs for A/A′ and X/X′ with different J values for the para-coupling ⁵J_A,X′.

This case further demonstrates that higher geometric symmetry not only applies to the theoretical NMR spin system but can be fully verified experimentally. Furthermore, it shows that the calculated weighted difference (residuals) between calculated and experimental spectra (RMS value, Figure 4) is highly sensitive to even subtle changes in the coupling constants. Panels A and B in Figure 4 show the overall RMS and the local, individual differences (relative root-mean-square [RRMS]), respectively, plotted vs the values for the para-coupling, J_A,X′. All other parameters were kept constant. While the para-coupling is the smallest coupling in the entire spin system and not readily “visible” in the spectrum, it still can be extracted with two-decimal precision, as shown in the table in Figure 4. Moreover, the iterative total-line-shape (TLS) fitting is highly reproducible when using different δ and J starting values (S5, Supporting Information). Notably, following the Nyquist–Shannon sampling theorem, the reproducibility of the process is well below half of the digital resolution of 65 mHz, which means that the fitting reliably converges on the same parameters. This means that the HiFSA process yields highly reproducible results independent of the starting values. However, due to the symmetry, the values for the ortho-coupling ³J_A,X and the para-coupling ⁵J_A,X′ as well as the values for the meta-couplings ⁴J_A,A′ and ⁴J_X,X′ can be exchanged without affecting the appearance of the spectrum. Therefore, it is important to check assignments to ensure consistency with the structure. It should also be noted that reproducibility at the mHz level should be tested by using different starting values for the HiFSA process, especially when parameters are strongly correlated (i.e., a change of one parameter is compensated by an opposite change of the other parameter, such as in the case of overlapping singlets). Instances have been reported where different J values can result in similar spectra especially when the achievable experimental line width is limited.²⁹

Finally, spectral processing, in particular apodization, has a small but measurable effect on the spin analysis. A summary of a systematic evaluation was performed for 4 using a variety of moderate line broadening and Gaussian resolution enhancement parameters and is shown in Table 1. While the variations are relatively small, falling within a 10–50 mHz range, the outcome suggests that the processing parameters should be reported in addition to the data acquisition conditions to ensure best reproducibility.

Table 1. Results of HiFSA Fitting^a of the HNMR Spectrum of Agnuside (4), Processed with Different Apodization Functions^b.

apodization	δA/A′ [ppm]	δX,X′ [ppm]	JX,X′ [Hz]	JA,X [Hz]	JX,A′ [Hz]	JA,A′ [Hz]
LB=0.0	7.918 211	6.841 087	2.6236	8.6065	0.3152	2.1881
LB=0.1	7.918 173	6.841 024	2.6044	8.6084	0.3234	2.2060
LB=0.2	7.918 172	6.841 028	2.5773	8.6059	0.3389	2.2243
LB=0.5	7.918 196	6.841 044	2.5580	8.6066	0.3398	2.2438
LB=–0.1, G = 0.1	7.918 147	6.841 008	2.6360	8.6072	0.3106	2.1801
LB=–0.2, G = 0.2	7.918 129	6.840 995	2.6372	8.6091	0.3111	2.1845
average	7.918 170	6.841 030	2.606 08	8.607 28	0.323 17	2.204 47
STDEVP	0.000 030	0.000 030	0.029 76	0.001 12	0.012 19	0.023 11

^aWith line-shape optimization.

^bExponential multiplication [factor: LB] and Gaussian enhancement [factors: LB and GF/GB].

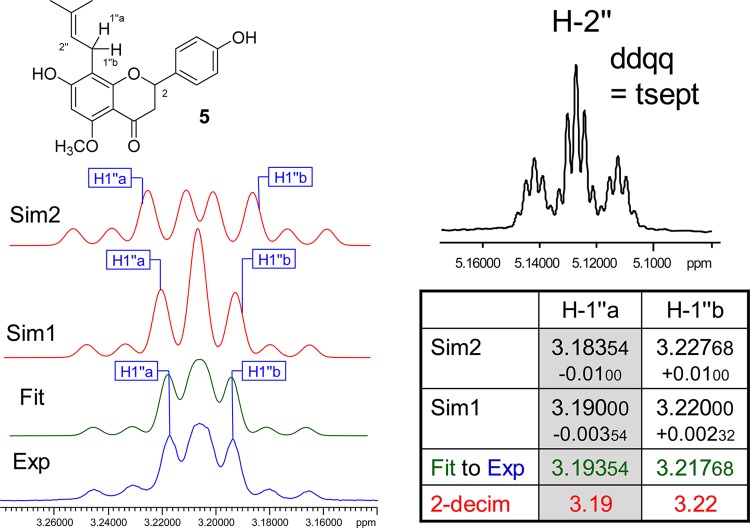
Case Study 5: Isoxanthohumol (5)

Prenyl groups are abundant in natural product scaffolds. Despite their simplicity and chemical shift dispersion due to the presence of an unsaturation, the nine protons of an underivatized prenyl group, i.e., two methyl groups, one olefinic, and one methylene pair, exhibit relatively complex HNMR signal patterns. Proton H-2″ gives rise to a highly characteristic fingerprint signal (Figure 5), appearing as a triplet of septets, which can be described as a ddqq and involves J-couplings within the entire prenyl moiety. Depending on the chemical anisotropy of the residue to which the prenyl group is attached, the methylene pair frequently becomes diastereotopic, either as a result of adjacent stereogenic centers and/or due to the anisotropy of nearby aromatic rings. Both are present in 5: the C-2 stereogenic center and the aromatic A- and B-rings of the flavanone core make the H-2″ methylene protons diastereotopic. While the anisotropy generates a relatively small difference of the chemical shifts (Δδ), it has a dramatic effect on the “multiplet” resonance pattern. Figure 5 shows the experimental and HiFSA fitted spectra. Even subtle changes in Δδ as small as 0.005 ppm are clearly visible (Figure 5, Sim1) and changes in the second digit result in a very different “multiplet” pattern (Figure 5, Sim2). The HiFSA profile is documented in S6, Supporting Information. As flavanones such as 5 frequently coexist in equilibria with their chalcone analogues (xanthohumol in the case of 5), the methylene diastereotopism can be used as an indicator of the cyclized form. Considering the biological implications of the chalcone–flavanone equilibria,³⁰ this exemplifies how an HNMR characteristic can become a probe and establish links to biological outcome.

Figure 5.

Case study 5: isoxanthohumol (5). Owing to the influence of the C-2 stereogenic center and the aromatic ring isotropy, the methylene protons H₂-1″ of 5 are diastereotopic. Accordingly, there are two resonances, H-1″a and H-1″b, which exhibit a small but important chemical shift difference (Δδ). While HiFSA fitting (Fit, in green) yields the precise spectral parameters, even small deviations of only the δ values lead to major changes in the simulated spectra and, thus, would impede dereplication. All J values were kept constant for the simulations (Sim, in red). A notable detail of the prenyl motif is the highly characteristic resonance of the olefinic proton, H-2″, which is coupled with all other protons in the prenyl moiety (500.163 MHz, methanol-d₄).

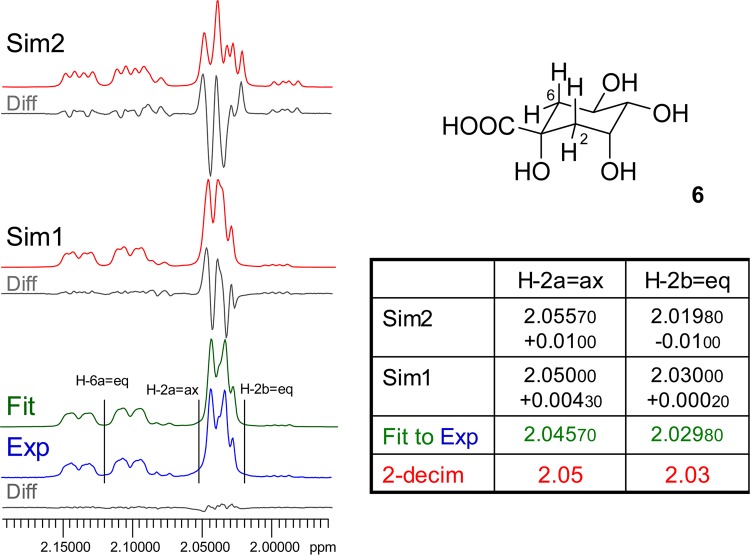
Case Study 6: Quinic Acid (6)

The hydroxylated cyclohexanoic acid, 6, is the core building block of a group of cinnamic acid derivatives that are found abundantly in plants. Owing to the chiral motifs found in the cyclohexane ring, all methylene protons in 6 and its congeners are diastereotopic. In addition to the occurrence of long-range couplings between the equatorial protons at C-2 and C-6,³¹ the small difference between the chemical shifts of the geminal protons at C-2 results in a pronounced non-first-order effect, leading to a complex multiplet pattern for the proton resonances (Figures 6 and S7, Supporting Information). Importantly, this affects not only the spin-particles of H-2a=ax and H-2b=eq, but also the multiplicity pattern of the neighboring signal of H-6a=eq, which shares a small ⁴J with H-2b=eq of 2.83 Hz. In addition to this W-coupling, the proximity of the chemical shifts of the C-2 methylene protons produces a virtual coupling effect, which leads to an additional “apparent” doublet splitting for which no coupling partner can be identified. This splitting is in fact virtual from a coupling pattern perspective and represents a special form of non-first-order spectra. Model calculations with the actual chemical shifts for H-2a/b rounded to two decimal places, i.e., small deviations of 0.0002 ppm for H-2a and 0.00430 ppm for H-2b only (Figure 6, Sim1), demonstrate that even such subtle misalignment shows significant differences when comparing the experimental with the calculated spectrum. Sim2 in Figure 6 represents the “worst case” scenario of a 0.01 ppm misalignment for both chemical shifts. All other parameters (J-couplings, line widths, and shapes) were kept constant during these calculations.

Figure 6.

Case study 6: quinic acid (6). Quinic acid derivatives, such as chlorogenic acid, formed by esterification with cinnamates occur widely in the plant kingdom and exhibit various degrees of diastereotopism of the C-2 methylene protons. As shown here for the core molecule, 6, the chirality induces a small but important chemical shift difference for H-2a vs H-2b. Only precise HiFSA fitting yields a congruent spectrum (Fit, in green), whereas even very small misalignments in the low ppb and even ppt range such as in Sim1 (Δδ of H-2a = 200 ppt, H-2b = 4.3 ppb) lead to mismatching of the resulting simulated spectra (360 MHz, methanol-d₄).

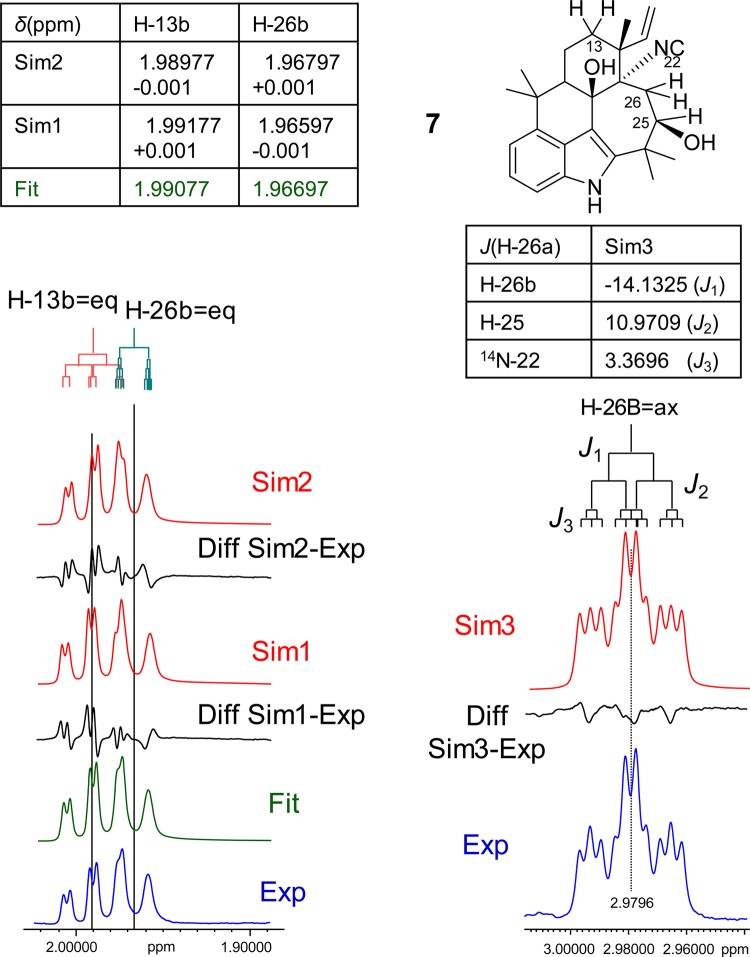
Case Study 7: Ambiguine N Isonitrile (7)

The isonitrile-containing indole alkaloid 7 is a member of the growing class of hapalindole alkaloids found in branched filamentous cyanobacteria. Representing a pentacyclic indole, 7 contains a rather rigid ring system with a seven-membered ring. The equatorial protons, H-13B, and the proton H-26B are positioned on opposite sides of the molecule and give rise to two strongly overlapping resonances (Figure 7). Although the two nuclei are not coupled to each other, the resulting resonance patterns are highly sensitive to δ shifts and highly characteristic such that they can serve as a (HiFSA) fingerprint for the entire molecule. A subtle change in the conformation is sufficient to cause significant changes in the chemical shifts and coupling constants of the two protons. The left portion of Figure 7 supports this hypothesis by showing a simulation experiment that implements a very subtle chemical shift difference (0.001 ppm for each proton) to the fully fitted HiFSA spectrum and observes the resulting effect on the spectrum. While this perturbation is 10 times lower than the commonly reported two-decimal precision for each, the induced changes are readily observed, as can be seen on the simulated spectra Sim1 and Sim2 in Figure 7. This demonstrates that complex signal patterns of closely resonating nuclei require at least ppb precision, even if the spins are not coupled.

Figure 7.

Case study 7: ambiguine N isonitrile (7). This case shows that high precision is required to properly document the resonances of two apparently “un(cor)related” protons in a molecule: although the two closely resonating protons, H-13b and H-26b, are not coupled to each other, perturbations as low as ±0.001 ppm (Sim1 + 2, in red) still have striking effects on the spectra compared to the experimental spectrum (Exp, in blue). A special feature of 7 is the heteronuclear ³J-coupling of H-26a with N-22, which is a rarely described property that actually can be used to distinguish molecules within alkaloid classes, such as the ambiguines: The spin-1 nucleus, ¹⁴N, gives rise to a triplet coupling pattern with a specific 1:1:1 line intensity (Sim3, in red). All J values were kept constant for the simulation (900 MHz, methanol-d₄).

Another intriguing observation can be made in 7. Upon closer inspection, the signal of the axial proton H-26A (Figure 7, right portion) shows an unexpected and rather complex splitting pattern. Reverting to the structure, the apparent multiple (long-range) coupling could not be linked to any other proton(s) in the molecule. This prompted consideration of heteronuclear coupling and eventually revealed that H-26A is involved in a ³J-coupling with the neighboring ¹⁴N nucleus of the isonitrile moiety. As a consequence of the coupling with a spin-1 nucleus, this leads to an additional signal splitting to triplets with a relative ratio of 1:1:1. After including the ¹⁴N spin-particle and its coupling into the HiFSA and spin simulation, the fully matching Sim3 spectrum was obtained (Figure 7). Moreover, it is evident that the line of the H-26B signal remains wider than that of its geminal partner. As different relaxation behavior can be excluded for this methylene pair, it is likely that H-26B is also coupled with the isonitrile nitrogen, albeit with a much smaller coupling that remains unresolved given the line width of the spectrum and the higher splitting pattern of the spin-1 coupling. The coupling of 1.134 Hz was taken into account when performing the HiFSA simulation shown in Figure 7 (see also S8, Supporting Information). While this generates a good match of the general shape of the H-26B signal relative to the experimental spectrum, a small difference remains around the center peaks of the two flanking triplets. However, it was also noted that one impurity was present in the sample, and its amount was determined to be ∼6% via subtraction of the HiFSA profile of 7. Further inspection of the difference spectrum showed that the small deviation in the H-26A signal matches quantitatively with an overlapping signal from the same 6% impurity. Ongoing studies are aimed at addressing the chemical shift, coupling, and overlap behavior of further members of this structural class.

Case Studies 8–10: Other Small Molecules with Complex HNMR Spectra

In the past, we have repeatedly observed instances where small natural product molecules exhibit rather complex HNMR spectra that required in-depth analysis to be fully compatible with the respective elucidated structures. The examples discussed briefly in the following provide additional evidence for the adequacy of reporting and interpreting HNMR data with enhanced precision.

Flavonoid Glycosides

The B-ring of the flavonoid moiety of the major kaempferol bisdesmoside from Arabidopsis thaliana (L.) Heynh. can be designated as an AA′XX′ or ABXY spin system. In the particular example of kaempferol-3-O-β-[β-glucopyranosyl-(1→6)glucopyranoside]-7-O-α-rhamnopyranoside (8),³² the anisotropism of the chiral sugar moiety leads to a small “inductive asymmetry” of the B-ring, expressed as a slight but significant difference in chemical shifts of the AA′ and XX′ pairs.³³ From the perspective of structure elucidation, the observed small chemical shift difference of about 1 Hz can confirm the presence of a chiral/anisotropic element in proximity to the B-ring. From the perspective of the HNMR parameters, this requires iterative spectral analysis and precise reporting to be reproducible. Analogous observations can be made for para-substituted aromatic rings in proximity to chiral anisotropic groups. The relevance of small substituent chemical shift (scs) differences due to intramolecular long-range shielding effects across up to 15 bonds has recently been confirmed³⁴ and further supports the significance of scs effects in the low Hz range.

Unsaturated Aliphatic Chains

In extended aliphatic chains, the protons of isolated double bonds can have close chemical shifts. This can produce highly complex resonances in which the relatively smaller cis J-couplings (ca. 10–12 Hz) cannot be readily distinguished from the larger trans-couplings (ca. 14–18 Hz). Such slight differences in chemical shifts can be predicted from the structure of the antimycobacterial lactone micromolide (9).³⁵ As noted at that time, dereplication of 9 using published NMR data was unsuccessful, making the ab initio structure elucidation necessary. Spectral simulation and iteration confirmed that the two cis-olefinic protons, C-9 and C-10, are affected by the slight asymmetry of the molecule, having a lactone vs a purely aliphatic tail attached on either side. This asymmetry causes a small but significant anisochronicity (Δδ 0.044 ppm) that required performance to be captured³⁵ and results in higher order and significant roofing effects for the dtt-like resonance pattern, forming the AB part of an ABMNXY spin system. Similar higher order effects were also observed in the two methylene protons at C-8 and C-11 immediately adjacent to the double bond. Overall, minute differences in the low ppb range modify the simulation enough to hinder accurate dereplication (S9, Supporting Information).

Terpenoid Skeletons

Finally, the classical example of the essential oil monoterpenoid carvone (10) is used to demonstrate how ppb chemical shift precision can be utilized to generate HNMR fingerprints for highly specific compound dereplication. In a previous study, the stereoselective scs effects of chiral lanthanide shift reagents had been utilized for enantiomeric discrimination of the optical antipodes of 10, which involved mapping of all proton resonances.³⁶ By completing the analysis of the complex A(MN)(RSTUV)Y₃Z₃ spin system consisting of 10 ¹H spins (S10, Supporting Information), the HNMR spectrum of 10 can now be reported with high specificity and reproducibly in a tabulated format. The tabulated parameters can serve as a template for further analysis, including the spectral simulation at any magnetic field strength. This not only simplifies structural dereplication, but also allows for quantification of major and minor components by qHNMR,^37,38 as recently demonstrated for the (iso)silybins from Silybum marianum (L.) Gaertn.²⁰ as well as ginkgolides and flavonoids from Ginkgo biloba L.¹⁴

Overall, the above case studies display some of the key characteristics that occur commonly in the HNMR of natural products, regardless of source, and organic molecules in general. Collectively, this makes the case for increased reporting precision as being critical for full reproducibility and optimal enablement of dereplication. The key characteristics can be summarized as follows:

• (i)the presence of highly coupled spin systems that cannot be analyzed under first-order assumptions (e.g., carbohydrates, glycosides, and aromatic rings);
• (ii)structural moieties with symmetric motifs that contain isochronic nuclei, but involve different spin–spin coupling patterns (e.g., aromatic rings, polyols, and meso compounds);
• (iii)complex “fingerprint regions” containing overlapping resonances of aliphatic skeletons, typically found in terpenoid moieties and other aliphatic groups, frequently occurring even at ultrahigh magnetic fields (≥800 MHz ¹H);
• (iv)diastereotopism of methylene protons with relatively small chemical shift differences, which are caused by stereogenic centers and/or aromatic anisotropy of nearby residues;
• (v)the occurrence of “virtual coupling”, i.e., splitting of resonances, that appear to be due to coupling but are in fact the result of non-first-order effects.

Recommendations

From the above case studies, the following general recommendations regarding the precision of HNMR reporting can be derived:

Chemical shifts (δ values) in ppm should be expressed with at least three decimal places (1 ppb), preferably four decimal places (0.1 ppb), especially when using (ultra) high-field NMR. Notably, this includes the referencing of the δ scale (see discussion of accuracy below).

Coupling constants (J values) in Hz should be expressed with at least one decimal place, preferably two decimal places (10 mHz), whenever data allows, keeping in mind that dynamics can be a limiting factor.

Especially when combined with the inclusion of raw NMR data (FIDs; time domain data), this format of HNMR reporting maximizes the utility of HNMR spectra for structural proof, dereplication, and reproducibility.

Discussion

Precision of HNMR Reporting

While a 0.01 ppm reporting precision has adequately reflected ¹H chemical shifts at magnetic field strengths equivalent to ¹H frequencies of ≤100 MHz in the past, in particular when using analogue data acquisition and hard copy spectra, it is inappropriate for contemporary NMR instrumentation with proton frequencies of ≥300 MHz and digital data management systems. Experimentally achievable precision is in fact much higher, as demonstrated in case study 2. Using peak top fitting, J values have previously been determined with precision as high as 1 mHz.³⁹ The fact that 10 mHz precision for J already translates into a 0.02 ppb chemical shift difference (at 500 MHz “average” ¹H frequency) further supports the proposal to report δ values in ppm with four decimal place precision. Moreover, it explains why the authors have encountered instances, such as in case study 4, in which even the fifth decimal place of δ values is experimentally achievable and justified, e.g., when higher order spin systems with significant Δδ values of <1 Hz at ≥800 MHz are encountered.

A further consideration relates to general rules of rounding: as rounding applies to the last reported decimal figure, the potential uncertainty resulting from a subsequent calculation (i.e., NMR simulation) will be twice the unit amount of that decimal level. Accordingly, it is important to match the precision of the method used to extract the spectral parameters with the precision of the experimental spectra. As demonstrated by the case studies above, computer-assisted spectral analysis, such as HiFSA, is one viable means of producing such a match, which is necessary for the closest reproduction of HNMR spectra and subsequent unambiguous structural dereplication.

Accuracy of HNMR Reporting and IUPAC

Consistent with IUPAC conventions,^40,41 chemical shift referencing in NMR uses internal tetramethylsilane (TMS, a highly volatile liquid; first introduced in 1958⁴²) for organic solvents or sodium-3-(trimethylsilyl)propanesulfonate (DSS) for aqueous solutions. In SI units, chemical shifts are measured in Hz. In their first comprehensive recommendations on NMR nomenclature in the post-CW, FT-NMR era from 2001,⁴⁰ plus an amendment from 2008,⁴¹ IUPAC makes the following definitions: (i) introduction of a field-independent scale with “...dimensionless scale factor for chemical shifts [which] should generally be expressed in parts per million”;⁴⁰ (ii) definition of the unit of the scale as “the factor of 10⁶ difference in the units of numerator and denominator [in the equation (eq. 6) defining δ in ppm, which] is appropriately represented by the units ppm”;⁴⁰ (iii) definition of the symbol δ for the chemical shift scale as a value with no units; (iv) reversion of the 1972 IUPAC recommendations⁴³ by revoking “that ‘ppm’ be not stated explicitly (e.g., δ = 5.00, not δ = 5.00 ppm)” as “this recommendation not to use “ppm” has not received acceptance in practice”.⁴⁰ With regard to the accuracy of δ scale reporting, IUPAC concluded in 2008, “On the basis of recently published results, it has been established that the shielding of TMS in solution ... varies only slightly with temperature but is subject to solvent perturbations of a few tenths of a part per million (ppm)”.⁴¹ This matches the exemplary use of two decimals in the 1972 document,⁴⁰ as well as standard practice in the literature.

However, it is important to point out that the IUPAC definition only establishes a connection between the δ scale and its accuracy, but not its precision. IUPAC only distantly refers to precision by noting that the definition of δ “allows values to be quoted also in parts per billion, ppb =10^–9 (as is appropriate for some isotope effects), by expressing the numerator in eq. 6 in millihertz (mHz)”. Considering that isotope effects are readily observed routinely in HNMR spectroscopy (e.g., the residual solvent signals of CD₃OD, i.e., CD₂HOD and CDH₂OD, are fully resolved from each other, separated by several Hz of baseline at 400–600 MHz), this already shows that the precision of the δ scale in HNMR is at least in the ppb (mHz) range.

Accuracy of HNMR Reporting and Internal Referencing

Because adding an internal reference has the general disadvantage of altering the sample (e.g., for subsequent biological testing), it is now widely customary, and a practice of convenience, to reference HNMR spectra to the residual solvent signal. The δ values of the residual solvent signals have been measured using neat NMR solvents with the addition of TMS or DSS and are widely available. Details about the variation of the ¹H chemical shifts [Δδ] of TMS in different solvents have also been reported.⁴¹ Obviously, when using this form of combined external and internal referencing, both measurements must be performed with equal precision and reported accordingly. Considering that internal referencing to solvent signals is practiced in laboratories globally, one important caveat is that numerous NMR solvent reference tables exist that differ substantially in the δ values assigned to a given solvent (e.g., for chloroform, 7.24 vs 7.26 are commonly found). In addition, the tables are typically restricted to two decimal precision. These two factors alone can introduce a confusing variation to reported NMR data and undermine both the precision and accuracy that NMR is well capable of achieving. Notably, the ability to “rereference” spectra by reprocessing of raw NMR data underscores the importance of repositories and sharing mechanisms for FIDs, e.g., in connection with publications (see also comments below). The further development of existing platforms and introduction of sharing mechanisms for the deposit, review, and exploitation of raw NMR data is critical and could follow the model of the Worldwide Protein Data Bank (www.wwpdb.org). A discussion of raw NMR file formats and an overview of software tools for NMR analysis are provided in S10, Supporting Information.

It is also important to emphasize the cautions that have to be taken when practicing referencing via residual solvent signals. The main caveats are associated with the fact that the solvent resonance can shift (Δδ) due to interactions with the analyte(s) in solution, with temperature, and with analyte concentration (mg/mL or μg/mL). Another important parameter can be salt concentration, affecting both shift and relaxation behavior and, thus, line width. Accordingly, for the specific use in dereplicating structures, NMR spectra need to be acquired under conditions in which these solvent dependencies are carefully controlled and/or internal TMS used for δ referencing. Also, critical to reproducibility is the reporting of the concentration (mg/mL or mM) of the sample. Notably, all these factors primarily affect the accuracy of the HNMR δ scale, rather than the precision.

As shown recently,⁹ a reasonably pure sample of progesterone (2), analyzed in a defined solvent, at defined temperature and pH yields highly accurate HiFSA profiles and fingerprints in which the experimentally matched quantum mechanical parameters can be determined with high precision and small error (<0.1%). However, unless dereplication of 2 is done under identical conditions and with a similarly pure sample, the chemical shifts resulting from HiFSA are highly precise, but not necessarily highly accurate (see accuracy discussion below). In contrast, the J values are both highly accurate and precise, as they depend much less on these physical and chemical factors. This means that differences in the impurity pattern and (co)solvent in the sample can impact the spectrum of an otherwise identical compound. This effect can be prominent enough that a previous HiFSA iteration may have to be repeated for a new sample in order to confirm the structural dereplication. Such confirmation requires much less effort, because the iteration can be started with near-perfect J values and mainly needs only slight adjustment of the δ values.

General Perspective for Structure Elucidation and Dereplication

The success of early (MS)-based structure dereplication methods, such as by GC-EI- and LC-ESI-MS, is rooted in the fact that unit-mass resolution MS spectra can be represented in a straightforward manner by x,y-matrices (m/z vs relative abundance). In the case of HNMR, the situation is considerably more complicated due to the following factors: (i) NMR lines are essentially nondiscrete, due to the inherent presence of signal splitting, occurrence of multiplet patterns, nuclear relaxation behavior, and residual field inhomogeneity; (ii) variation of line widths within a spectrum, reflecting the dynamic nature of molecular structure; (iii) lack of dispersion resulting in signal overlap; (iv) presence of higher order effects, resulting in complex relative line intensities. Collectively, this renders the simple x,y-tabular representation of HNMR spectra inappropriate and can considerably complicate numerical data representation, even beyond multidimensional matrices. A further confounding factor is that shape and intensities of HNMR resonances depend not only on ¹H nuclear parameters (mainly δ and J values) but also on the parameters of other (hetero)nuclei present in the same spin system (see Case Study 7). This phenomenon becomes important when considering the well-established, but often overlooked higher order spin-coupling effects, which largely depend on the relative chemical shifts (Δδ) and magnitudes of coupling constants (values of J) of the nuclei in a given spin system. Characteristic visual effects frequently observed in HNMR spectra are “roof”, “tilt”, and “virtual coupling” effects.⁴⁴ These higher order effects are in fact diagnostic and provide additional structural connectivity information that is unavailable via first-order interpretation.

Consequently, the common forms of tabular reports of HNMR data with designated multiplicities frequently represent a(n) (over)simplified visual description and fail to reflect the rich information that is actually present in an HNMR spectrum. Thus, even though the commonly used d/t/q multiplicity descriptors reflect the underlying ¹H spin system, it is difficult in practice to correlate the observed resonance pattern with a simple d/t/q-based description. The well-established⁴⁴ but frequently overlooked discrepancy between observed resonance frequencies (line distances and locations) and J and δ values deduced by first-order (“visual”) analysis adds considerably to this complication. This may explain the abundance of the term “multiplet” (m) in the literature, an observation that may even be used to justify the limited precision in reporting of HNMR parameters.

Fortunately, NMR spectra follow well-established quantum mechanical rules. Provided all relevant NMR parameters of a spin system are known, ¹H NMR spectra can be calculated (simulated; not to be confused with predicted, see Glossary of Terms) for any natural line width and, notably, for any given magnetic field strength. Contemporary software tools for NMR spectral simulations are readily available and permit the simulation of spectra involving multinuclear spin systems. The choice of appropriate tools will depend on the number of possible spin-particles as the computational complexity escalates rapidly as a function of the numbers of spins. Typically, each spin-1/2 nucleus adds a factor of 8 to the computation time (see ref (25) for details regarding spectral simulation). Therefore, software programs are required to approximate negligible terms and, whenever possible, divide the spin systems into subsystems when calculating systems consisting of more than 12 fully coupled spins. The latter is the typical threshold where the quantum mechanical calculations become impractical with contemporary computing resources. This is mainly a result of excessive CPU time and not of CPU bus width (16/32/64 bit), and recent developments using GPUs as supercalculators may lead to new opportunities.

Simulation of Replica HNMR Spectra

Taking a practical user perspective, Table 2 summarizes the essential HNMR parameters that are required for NMR spectral simulation. Once a complete parameter set is available for a given compound, the quantum mechanical calculation is capable of generating an exact replica⁹ of the HNMR spectrum. The ability to perform such calculations for any magnetic field strength makes simulation and HiFSA a powerful tool for structure dereplication. In addition, the ability to accommodate past, present, and future magnetic field strengths enables the perpetuation of documented NMR data along the continued path of NMR spectrometer evolution.

Table 2. Essential Parameters for the Comprehensive Tabulated Description and Generation of Simulated Replicas of Experimental HNMR Spectra.

parameter	description
all 1H chemical shifts	δ [in ppm]; reported with 1 ppb, preferably 0.1 ppb, precision
all scalar coupling constants	J [in Hz], including the sign of J; reported with at least one, preferably two, decimal places precision
magnetic field	field strength [in T] or frequency [in MHz for 1H]
signal line shape	Lorentzian/Gaussian contributions to each resonance, containing the relaxation properties (T1 and T2)

Field Strengths and the Congruence of Simulated and Experimental HNMR Spectra

The presence of any significant differences between simulated and experimental spectra indicates the incompleteness of and/or errors in the parameter set and spectral interpretation. Conversely, total congruence between simulated and experimental spectra is an indicator of comprehensive interpretation of experimental HNMR data. This demonstration of congruence is a prerequisite for the accurate determination of chemical shifts and J-couplings from higher order spectra.⁴⁵⁻⁴⁷

In early days of NMR, when only relatively low magnetic field strengths (1.4–2.3 T/60–100 MHz for ¹H) were available, spectral simulation was frequently performed to confirm or even enable spectral interpretation. At the time, a 0.01 ppm uncertainty was typically less than the achievable line widths (∼1.0 Hz). While this may explain the historic reason for reporting only two decimal places for δ_H, it does not bode well on the fact that in contemporary magnets 0.01 ppm translates into several Hz, which is equivalent to a larger H,H-coupling and/or well-resolved signals. The advent of high- and ultra-high-field magnets has increased spectral dispersion and transformed many—but by far not all—HNMR spectra into first-order spectra. Notably, this development does not affect the determination of NMR spin parameters, as the underlying “residual” higher order nature even of ultra-high-field HNMR spectra can significantly impact their precise determination and, thus, the aspect of reproducibility discussed here. Another important consideration is the challenge of analyzing increasingly complex molecules, which has been counterbalancing the availability of higher NMR magnetic fields. Thus, the complexity of commonly analyzed structures maintains the need to consider full-spin analysis in HNMR interpretation, not only because of higher order effects but also due to the persistence of signal overlap in HNMR.

The essential absence of full-spin HNMR analyses in the contemporary literature explains why structure dereplication almost always requires a complete reanalysis of previously analyzed samples and/or reinterpretation of previous experiments, overall leading to an inefficient work flow. Thus, in order to facilitate rapid HNMR-based structural dereplication and enable a tabulated reporting format of HNMR data, two essential requirements must be fulfilled: (i) completeness: the tabulated data must fully represent the relevant NMR parameters of all involved spin systems; (ii) precision: the data must be sufficiently precise to match the resolution and chemical shift dispersion of the experimental data (see Recommendations). Only then will NMR simulation yield a spectrum that is identical with the experimental NMR data.

Heteronuclear Couplings

It is noteworthy that, in principle, full-spin analysis requires the inclusion of heteronuclear couplings. In practice, relatively high natural abundance nuclei, fluorine (¹⁹F) and phosphorus (³¹P), are relevant. Case study 7 serves as an example where the high-abundance (99.56%%) spin-1 nucleus, ¹⁴N, can even be key to the full understanding of an HNMR spectrum. It also shows that heteronuclear coupling effects are not restricted to spin-1/2 nuclei. However, the present study ignores the influence of ¹H, ¹³C couplings due to the low abundance of ¹³C and focuses on the simulation of ¹H spin systems that are bound only to ¹²C. The general availability of broad-band (BB) ¹³C decoupling on contemporary NMR spectrometers, such as via the ¹³C-BB GARP decoupling method,⁴⁸ provides a routine approach for collapsing the ¹³C satellites. The resulting ¹H NMR spectra are free of ¹³C satellites and also produce HNMR spectra suitable for quantification (qHNMR). Finally, ¹³C-heterodecoupling also eliminates potential problems of small but significant distortions of resonances that coincide with the ¹³C satellites of high-abundance resonances such as methyl, isopropyl, and tert-butyl groups.

Summary and Conclusions

Contemporary structural analysis and future dereplication efforts place an increased demand on both the precision and the completeness of HNMR analyses. Following the accepted paradigms of structure elucidation workflows, especially those that heavily depend on indirect evidence (deductive reasoning) due to an absence of X-ray crystallographic or visualized molecular information (e.g., as achievable by atomic force microscopy^49,50), the interpretation of an HNMR spectrum is to be pursued to a depth where no further inconsistencies associated with the chemical structure are conceivable. Whether or not the use of deductive reasoning requires a full ¹H spin analysis (HiFSA) may strongly depend on the complexity of the problem and the availability and weight of further spectroscopic results, such as those from 2D NMR and other spectroscopic information. Contemporary NMR instrumentation facilitates the acquisition of ¹H, ¹³C correlation spectra, which can be developed into powerful dereplication tools. Recent examples are the simplification of the widespread HSQC into a pure-shift HSQC experiment⁵¹ and the use of HMBC and HSQC for 2D barcoding and differential analysis of mixtures.⁵² However, as the 1D HNMR spectrum is a core element of any structure elucidation workflow, its proper interpretation and documentation are inevitable.

Computer-assisted structure elucidation (CASE)⁵³ has received much attention recently. In part driven by metabolome research, public NMR databases and other platforms for sharing NMR spectra in their genuine binary format have become available such as nmrshiftdb.org,⁵⁴nmrdb.org,⁵⁵bmrb.wisc.edu,⁵⁶hmdb.ca, chemspider.com,⁵⁷sdbs.db.aist.go.jp, mmcd.nmrfam.wisc.edu,⁵⁸bml-nmr.org,⁵⁹ and harned.chem.umn.edu.⁶⁰ Regardless of the depth of ¹H NMR interpretation, however, future dereplication and metabolomic identification efforts will always rest on the adequate documentation of the original spectra. Considering their routine availability and high information content, high-resolution HNMR spectroscopy (supported by the results from MS studies) are, in principle, ideally suited for the dereplication of organic molecules, provided the spectra are properly conserved and reported.

Despite the availability of digital tools for NMR data storage and visualization (e.g., http://nmrwiki.org/wiki/index.php?title=Databases), the traditional paper and electronically printed (PDF) format continues to be the major mechanism for public dissemination of NMR spectroscopic data. As detailed above, the conversion from their genuine graphical (spectral) to alphanumeric (tabular) formats is a crucial step, and the present study shows how inaccuracies can result from inadequate precision during and/or approach to this process. The proposed precision of four decimal δ in ppm and one to two decimal J in Hz for HNMR interpretation and reporting will ensure that tabulated HNMR data fulfill the minimum criteria for dereplication. When paired with spectral simulation and confirmative iteration, which are required for minor adjustments of Δδ effects (see above), properly (re)presented HNMR data enable rapid structure dereplication. It is important to note that confirmative iteration is typically a simple process during which J-coupling patterns are kept constant, while mainly accounting for the minor variations of the chemical shifts that occurr when comparing different samples, analyzed in different laboratories, and under different conditions. This process takes full advantage of the tabulated precise δ/J HNMR data sets and overcomes the limitations of chemical shift accuracy (see sections above). Importantly, as simulation can accommodate any magnetic field, these considerations apply across all available instrumentation. This capacity increases the universal nature of HNMR as a dereplication tool that yields portable dereplication data.

Precise δ/J parameter sets extracted from HNMR spectra are essential for the structural dereplication of both newly described and reisolated natural products, independent of their taxonomic source. Because the underlying rationale applies universally to organic molecules, adequate precision in HNMR reporting enhances the reproducibility of research in related fields, such as organic synthesis and analytical and biological chemistry. As many contemporary scientific challenges require multidisciplinary approaches that connect data from various disciplines, the reproducibility of a factor as basic as chemical composition becomes even more critical. Therefore, refined HNMR data can make a valuable contribution to the advancement of natural products and related life sciences.

Experimental Section

Samples

The compounds in this study have been isolated and characterized previously in the authors’ laboratories, as per the respective references, or were sourced as indicated: uzarigenin-3-sulfate (1; 9 mg);^26,61,62 progesterone (2; 3.0 mg);^9,28 syringetin-3-O-β-d-glucoside (3; 3 mg) (source: Chromadex, Irvine, CA, USA); agnuside (4; 9.1 mg);⁶³ isoxanthohumol (5; 10 mg);^64,65 quinic acid (6; 20 mg);^31,66 ambiguine N isonitrile (7; 1.0 mg);⁶⁷ kaempferol-3-O-β-[β-glucopyranosyl-(1→6)glucopyranoside]-7-O-α-rhamnopyranoside (8; 9.0 mg);³² micromolide (9; 59 mg);³⁵ carvone (10; 20 mg).³⁶

NMR Spectroscopy

The proton NMR spectra were recorded on various spectrometers from 900 to 300 MHz (¹H frequency) at 298 K using the basic pulse zg sequence, typically with 30 degree flip angles: Bruker (Billerica, MA, USA) AVANCE AVII900 MHz (21.0 T) and AVANCE DRX600 MHz (14.0 T) spectrometers equipped with 5 mm TCI and TXI inverse detection cryoprobes; Varian Unity 600 (14.0 T) with 5 mm multinuclear probe; Bruker AVANCE DRX500 MHz (11.7 T); Bruker AM 360 (8.4 T) and AVANCE DPX300 MHz (7.0 T) with 5 mm broadband probes. The 1D ¹H NMR digital resolution was generally greater than 0.1 Hz, equivalent to 0.000 25 ppm (64K real data points, 12 ppm spectral width at 400 MHz). Chemical shifts (δ in ppm) were referenced to the residual solvent signals (CHCl₃ in CDCl₃ at δ 7.2400; CD₂HOD in CD₃OD at δ 3.3000), and coupling constants (J) are given in Hz. Off-line data analysis was performed using the NUTS, MestReNova, and PERCH software packages by Acorn NMR Inc. (Livermore, CA, USA), Mestrelab Research (Santiago de Compostela, Spain), and PERCH Solutions Ltd. (Kuopio, Finland). Lorentzian–Gaussian resolution enhancement was performed using LB and GB values of −0.5 to −3.0 and 0.05 to 0.30, respectively.

Spectral Simulation and Iterative Full-Spin Analysis

This analysis utilized QMTLS iterators available within the PERCH NMR software version 2013.1 (PERCH Solutions Ltd.). The ¹H iterative full-spin analysis was performed using the automated consistency analysis (ACA) available in the same software package. The difference spectra were calculated using the plot/print module built into this software as well.

Glossary of Terms

Prediction: generation of NMR chemical shift and coupling information from a given structure. Simulation: the quantum chemical calculation of an NMR spectrum from all relevant NMR parameters (chemical shifts, couplings, magnetic field strength, line width, line shape, and consideration of relaxation properties). Iteration: the optimization of initially given NMR parameters to match the experimental data using an iterative approach, thereby minimizing the difference between calculated and experimental spectrum. RMS: root-mean-square; for two spectra it is computed by calculating the RMS of the differences between corresponding points in each spectrum. RRMS: regional RMS; localized RMS for a certain subsection of the spectrum (frequently a multiplet), following the same calculation as for the RMS of the whole spectrum. Dereplication: structural identification of a known chemical entity based on previously reported analytical/spectroscopic information.

Supporting Information Available

The HNMR spectroscopic data, HiFSA profiles and fingerprints, as well as simulations for compounds 1–7, 9, and 10. This material is available free of charge via the Internet at http://pubs.acs.org. Further Supporting Information is distributed via the corresponding author’s web pages at http://go.uic.edu/gfp.

Author Present Address

^§ 1419 Appleberry Way, West Chester, PA 19382, USA.

Author Present Address

^∥ Wm. Wrigley Jr. Company, Chicago, IL 60642, USA.

The authors declare the following competing financial interest(s): M.N., J.L., and S.P.K. are part/full-time employees at Perch Solutions Ltd. The other authors declare no competing financial interest.

Notes

This paper represents part 25 of the series on Residual Complexity and Bioactivity (see http://go.uic.edu/residualcomplexity).

Funding Statement

National Institutes of Health, United States