Fig. 6.
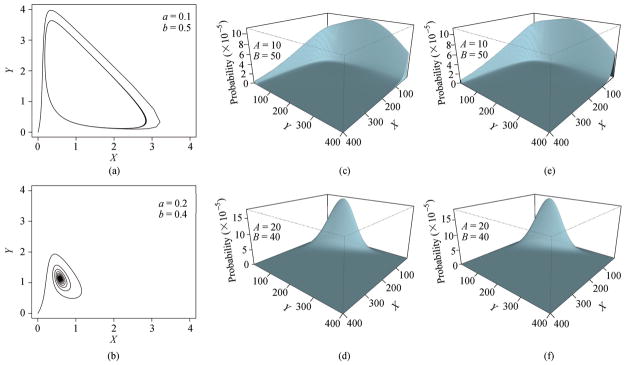
Calculated steady state probability distributions over different copy numbers of X and Y and the trajectories of evolving concentrations of X and Y of the Schnakenberg model. (a) and (b): Trajectories of evolving concentrations of X and Y according to the deterministic ordinary differential equation (ODE). Here (a) shows the well-known oscillating limit cycle behavior of the Schnakenberg model, and (b) shows the convergence towards a fixed point. The concentrations of A and B are set at values equivalent to the copy numbers used in stochastic models. (c) and (d): Reconstructed probability distributions over X and Y obtained from 200 000 simulations of the Langevin equation (LE). (e) and (f): Exact probability distributions over copy numbers X and Y obtained by solving the chemical master equation (CME). Two sets of copy numbers of (A, B) at (10, 50) and (20, 40) are used for the fixed parameters A and B (adapted from [68]).
