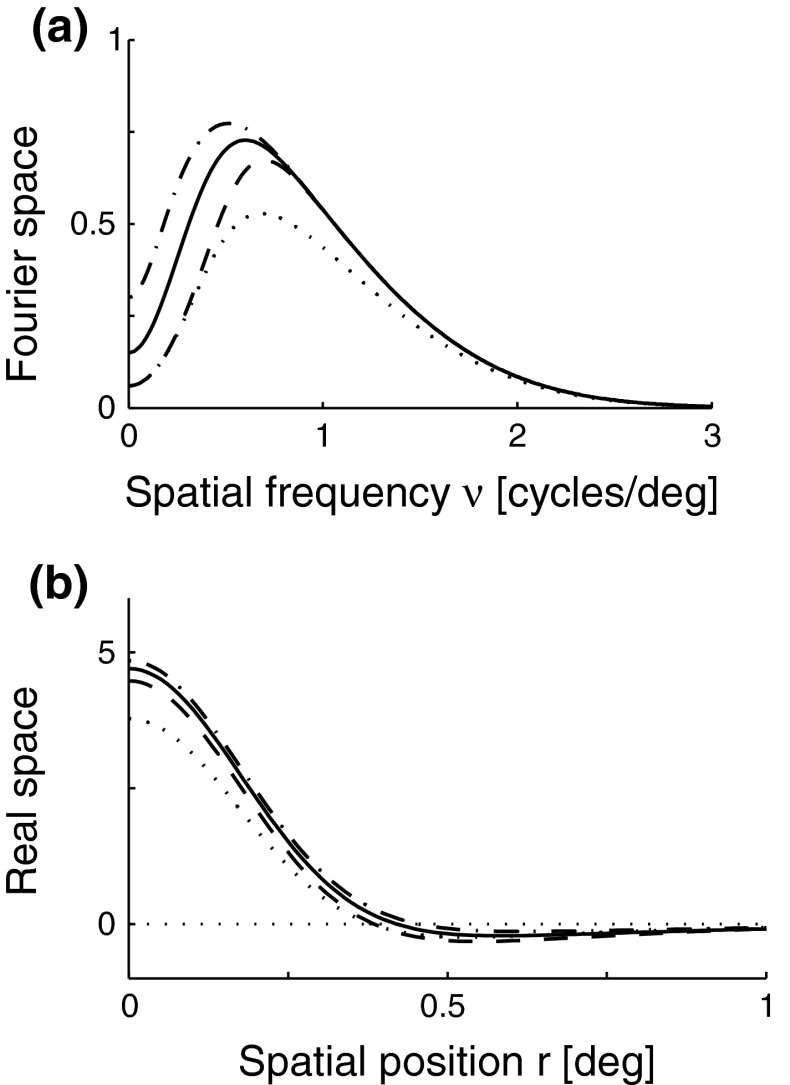
Fig. 5.
Examples of eDOG spatial receptive fields (spatial impulse-response function) in the “fast-loop” limit. a eDOG function in Fourier space, 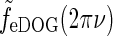 , in Eq. 34 plotted as a function of spatial frequency ν (k = 2π ν). Solid line: C = 0, i.e., standard DOG. Dash-dotted line: Push-pull excitatory feedback for C = 0.5, c = 0.83 deg. Dashed line: Push-pull inhibitory feedback for C = −1.5, c = 0.83 deg. Dotted line: Modified push-pull inhibitory-feedback eDOG model with the Gaussian loop-function replaced with a function of the type in Eq. 24 with the constant
, in Eq. 34 plotted as a function of spatial frequency ν (k = 2π ν). Solid line: C = 0, i.e., standard DOG. Dash-dotted line: Push-pull excitatory feedback for C = 0.5, c = 0.83 deg. Dashed line: Push-pull inhibitory feedback for C = −1.5, c = 0.83 deg. Dotted line: Modified push-pull inhibitory-feedback eDOG model with the Gaussian loop-function replaced with a function of the type in Eq. 24 with the constant 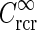 set to −1.5,
set to −1.5, 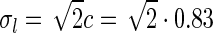 deg
deg 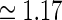 deg and σn = 0. b Real-space eDOG functions, f
eDOG(r), corresponding to the Fourier-space functions in left panel. The DOG parameters used are A
1 = 1, a
1 = 0.25 deg, A
2 = 0.85, and a
2 = 0.83 deg
deg and σn = 0. b Real-space eDOG functions, f
eDOG(r), corresponding to the Fourier-space functions in left panel. The DOG parameters used are A
1 = 1, a
1 = 0.25 deg, A
2 = 0.85, and a
2 = 0.83 deg