Assessment of the reliability of standard automated perimetry in regions of glaucomatous damage

Abstract

Purpose

Visual field testing uses high contrast stimuli in areas of severe visual field loss. However, retinal ganglion cells saturate with high contrast stimuli, suggesting that the probability of detecting perimetric stimuli may not increase indefinitely as contrast increases. Driven by this concept, this study examines the lower limit of perimetric sensitivity for reliable testing by standard automated perimetry.

Design

Evaluation of diagnostic test.

Participants

34 participants with moderate to severe glaucoma (Mean Deviation (MD) on their last clinic visit averaged −10.90dB, range −20.94dB to −3.38dB). 75 of the 136 locations tested had perimetric sensitivity ≤19dB.

Methods

Frequency of seeing curves were constructed at four non-adjacent visual field locations by the method of constant stimuli (MOCS), using 35 stimulus presentations at each of 7 contrasts. Locations were chosen a priori, and included at least two with glaucomatous damage but sensitivity ≥6dB. Cumulative Gaussian curves were fit to the data, first assuming a 5% false negative rate, and subsequently allowing the asymptotic maximum response probability to be a free parameter.

Main Outcome Measures

The strength of the relation (R²) between perimetric sensitivity (mean of last two clinic visits) and MOCS sensitivity (from the experiment), for all locations with perimetric sensitivity within ±4dB of each selected value, at 0.5dB intervals.

Results

Bins centered at sensitivities ≥19dB always had R²>0.1. All bins centered at sensitivities ≤15dB had R²<0.1, an indication that sensitivities are unreliable. No consistent conclusions could be drawn between 15–19dB. At 57 of the 81 locations with perimetric sensitivity <19dB, including 49 of the 63 locations ≤15dB, the fitted asymptotic maximum response probability was <80%, consistent with the hypothesis of response saturation. At 29 of these locations the asymptotic maximum was below 50%, and so contrast sensitivity (50% response rate) is undefined.

Conclusions

Clinical visual field testing may be unreliable when visual field locations have sensitivity below approximately 15–19dB, due to a reduction in the asymptotic maximum response probability. Researchers and clinicians may have difficulty detecting worsening sensitivity in these visual field locations and this difficulty may occur commonly in glaucoma patients with moderate to severe glaucomatous visual field loss.

Automated white-on-white perimetry remains the clinical standard for objective assessment of function in glaucoma. However, the test-retest variability is considerable, and worsens with greater damage.^1–12 This necessitates repeated visual field testing when establishing a diagnosis of glaucoma or when ascertaining disease progression.^13–17 For example, variability in patients with ocular hypertension required three confirmatory visual fields to reliably detect progression.¹⁸ Studies in patients with glaucoma or ocular hypertension suggest that about six visual fields may be required to assess the rate of visual field progression.¹⁴ Overall, the variability of visual field sensitivity, especially in glaucoma patients, may delay detection and treatment of progressive glaucomatous visual field loss.

Static perimetry uses a contrast stimulus that, when presented, causes an increase in the firing rate of functioning retinal ganglion cells (RGCs). Ganglion cell axons transmit these action potentials to the visual cortex, via the lateral geniculate nucleus. As stimulus contrast is increased, RGCs increase their firing rate, eventually reaching the point at which the observer detects and responds to the stimulus.¹⁹ The generation of action potentials is probabilistic, in that their exact timing cannot be predicted, and it is common to report the mean number of spikes within a set time period across repeated stimulus presentations. Due to this and other factors, in eyes free of disease the probability of responding to a stimulus increases gradually from 0% for stimuli several decibels higher (lower contrast) than threshold to 100% for stimuli several decibels lower (higher contrast) than threshold. The psychometric function, describing the probability that the observer will respond to a stimulus of a given contrast, is known in perimetry as the frequency-of-seeing (FOS) curve. In clinical perimetry, contrast sensitivity is defined as the reciprocal of the contrast that the subject will respond to on 50% of presentations. To maintain an acceptable test duration and avoid overly fatiguing the patient, this sensitivity is typically estimated based on fewer than ten presentations (usually substantially fewer) per location.²⁰

Contrast sensitivities from automated perimetry are reported on a decibel (dB) scale. In standard static automated perimetry, a 10dB increase corresponds to a log unit decrease in contrast. 0dB represents the instrument-dependent maximal contrast that can be presented by the perimeter. Therefore with the commonly used Humphrey Field Analyzer (HFA; Carl Zeiss Meditec, Dublin, CA, USA), a sensitivity of 0dB indicates that the subject would respond to half of the stimuli presented at 317,000% contrast, whereas for an Octopus perimeter (Interzeag / Haag Streit, Koeniz, Switzerland) 0dB corresponds to 135,000% contrast. Throughout this manuscript, to avoid confusion, we will use HFA dB units, i.e. 0dB=317,000% contrast, such that the lower limit for the Octopus perimeter becomes 3.7dB. We will refer to these 0dB values as the ‘technical’ lower limit of the stimulus range of each perimeter.

However, the lower limit of the “reliable stimulus range”, defined as the range over which reliable measures of sensitivity can be obtained by perimetry, may be higher than this.²¹ At low sensitivities, the test-retest variability increases substantially.^{1–3, 5, 7–12} When sensitivity has deteriorated to the point that it is reported as being 15dB, the 95% confidence interval for the retest sensitivity at the same location covers more than half of the technical stimulus range of the perimeter.^{7, 22} This limits the utility of perimetry when sensitivity is low. This unreliability may not entirely be due to false positives, false negatives or fixation losses. We refer to sensitivities as being “unreliable” when a change in reported sensitivity is not necessarily related to true change, and so the results are of very limited clinical use. The reasons for the increase in variability are still unclear. Improved understanding of this sensitivity-variability relation should aid endeavors to reduce the variability, and may also provide useful insights into some pathophysiological aspects of glaucoma.

The responses of healthy RGCs saturate when high contrast stimuli are presented.^{23, 24} Instead of the rate of generated action potentials increasing proportionately to contrast, it asymptotes to a maximum rate, due to factors including the cell’s refractory period. This response rate can be modelled according to a Michaelis-Menten function.^25–27 The implication is that when the firing rate approaches its asymptotic maximum due to a high contrast stimulus being presented, increasing the contrast still further has little effect on the firing rate. If the RGC firing rate does not increase, the signal received by the visual cortex cannot increase, and so the subject’s response probability should not increase. In the presence of such response saturation, any change in response probability as stimulus intensity increases is most likely due to response errors, eye movements or light being scattered on to neighboring photoreceptors and RGC receptive fields, rather than being caused by a change in the responses of individual RGCs at the tested location. Some stimuli may be detected at contrasts considerably lower than the ‘true’ threshold, whereas a proportion of considerably more intense stimuli will not be detected. This inherent physiologic unpredictability provides a feasible explanation for the flatter FOS curves and hence the higher variability that is observed when conducting static increment perimetry at locations with low sensitivity.^{1, 10}

RGC saturation also implies that at locations with more severe damage, even if all remaining RGCs attain their asymptotic maximum firing rate, this reduced number of RGCs may not produce a sufficiently strong cortical signal to guarantee detection. The response probability could then remain below 100%. At some of those locations, the asymptotic maximum response probability could be below 50%, implying that even though some function remains at that location (because the response probability is above zero), the contrast sensitivity in its most common formulation is undefined. According to this hypothesis, once a visual field location has deteriorated to these levels, perimetric sensitivities would be inherently unreliable. The estimated sensitivity will be influenced by response errors, small eye movements and light scatter, but could contain little information concerning the true level of remaining function.

In this study, we measure FOS curves from glaucoma patients in regions of the visual field with low sensitivity. Swanson et al reported that in non-human primates, semi-saturation of RGCs (the point at which RGCs respond at half their asymptotic maximum firing rate) occurred at 24 ± 2dB.²⁴ We therefore concentrate on locations with perimetric sensitivities that are below this level but are still non-zero (such that some function remains). We aim to determine the contrast beyond which perimetric sensitivities become unreliable, and so further changes in the reported sensitivity may not be related to true disease progression. This contrast can then be interpreted as the effective lower limit of the reliable stimulus range of static increment perimetry (although a reported sensitivity of ‘<0dB’ indicating that the subject did not respond even to the highest available stimulus contrast could still reliably indicate lack of measureable function). Our results will aid in the understanding of perimetric variability, and also inform researchers and clinicians about the ability to detect visual field progression at locations already substantially damaged by glaucoma.

Methods

We recruited subjects with moderate to severe primary open-angle glaucoma from a tertiary glaucoma clinic at Devers Eye Institute. Inclusion criteria were a diagnosis of primary open-angle glaucoma as determined by their clinician, and at least two non-adjacent visual field locations with sensitivity from standard automated perimetry between 6–18dB on both of their two most recent clinic visits (HFA, 24-2 test pattern, SITA standard algorithm). Exclusion criteria were an inability to perform reliable visual field testing, best-corrected visual acuity worse than 20/40 (since this could cause difficulties with maintaining fixation), cataract or media opacities likely to significantly increase light scatter, or other diagnoses or medications that may affect the visual field. All protocols were approved and monitored by the Legacy Health Institutional Review Board, and adhere to the Health Insurance Portability and Accountability Act of 1996 and the tenets of the Declaration of Helsinki. All participants provided written informed consent once all of the risks and benefits of participation were explained to them.

For each subject, four test locations from the 24-2 visual field test pattern were chosen based on reviewing their two most recent clinical visual field test results (conducted on an HFA perimeter). The most recent clinic visit occurred on average 169 days prior to the study visit. At least two of the chosen locations had significantly reduced sensitivity that was no lower than 6dB (to ensure that some function remained at that location), with the remaining locations chosen in different regions of the visual field to promote fixation stability. Testing several locations within the visual field also ensures spatial uncertainty, which will increase the slope of the FOS curve by preventing attention being focused on a single location,²⁸ and make the test conditions more similar to clinical perimetry.

FOS curves were assessed using the Method of Constant Stimuli (MOCS) on an Octopus perimeter.²⁹ At each test location, “Perimetric Sensitivity” was defined as the mean of the sensitivities measured at that location on the subject’s two most recent clinical visual field examinations. For the two less damaged locations of the four, seven contrasts were chosen for testing, set at 3dB intervals centered at the perimetric sensitivity (i.e. so that the range ±9dB from this value is covered). If perimetric sensitivity was below 12.7dB then the seven contrasts were instead centered on this value, i.e. covering the range 3.7dB – 21.7dB. This meant that the greatest contrast to be tested at such locations (lowest on the dB scale) would be 3.7dB, which was the highest intensity stimulus available on the Octopus perimeter used (3.7dB on an HFA scale is equivalent to 0dB on the Octopus perimeter’s native scale). For the two most damaged locations of the four selected for a given eye, the highest contrast stimulus to be tested was always set to 3.7dB, and the lowest contrast to be tested was set to 28.7dB, so that there were common contrast levels between all subjects. The remaining five intermediate contrasts were set at 3dB intervals centered on the perimetric sensitivity (or centered on 12.7dB) as before.

Size III stimuli were presented using an Octopus 900 perimeter, externally controlled using the Open Perimetry Interface.³⁰ This system allows a specified stimulus to be presented, with the perimeter returning information about whether the subject pressed the response button within a designated response window, which was set as being up to 800ms after the end of the stimulus. Stimuli were presented for 200ms, as is standard in static increment automated perimetry when using the HFA perimeter, in order to provide the most direct comparison with the subjects’ clinical results. The subject was also required to undergo the same amount of dark adaptation as they would in clinic.

We programmed the perimeter to present seven repetitions at each of the seven chosen contrasts for each of the four chosen locations, plus five blank presentations, i.e. a total of 201 presentations in one run. Five runs were completed, with the order of presentations randomized within each run for both contrast and location. This meant that the total number of stimulus presentations over the five runs was 35 per contrast level per location, resulting in 245 presentations per FOS curve. The 25 blank presentations across the five runs were used to estimate the false positive rate. The number of presentations was chosen such that each of the five runs took approximately 6 minutes, similar to the duration of a clinical SITA standard visual field test. To reduce fatigue, the subject was allowed to take breaks between runs, provided they regained adaptation before recommencing testing.

Once testing had been completed, the proportion of stimuli to which the subject responded averaged across the five runs was calculated for each of the seven contrasts per test location. A cumulative Gaussian curve was fit to each set of FOS data, such that the response probability was given by:

• FP + (1-FN-FP)*Φ((C-CS)/SD)

FP represents the false positive rate, taken as the proportion of the 25 blank stimuli to which the subject responded. C represents the contrast of the stimulus in dB. Φ represents the cumulative Gaussian distribution, such that Φ(−∞)=0 and Φ(∞)=1. CS represents the contrast sensitivity in dB, i.e. the contrast that the subject would respond to on 50% of presentations. SD represents the standard deviation of the cumulative Gaussian, such that a higher value of SD gives a flatter FOS curve. The values of CS and SD were fit by constrained maximum likelihood estimation, with CS constrained to be greater than −10dB (to ensure algorithmic convergence) and SD constrained to be greater than zero. All analyses were performed using the statistical programming language R (R Foundation for Statistical Computing, Vienna, Austria).

In the primary analysis, FN was taken as the false negative rate, i.e. the probability that the observer sees a stimulus but fails to respond. Since this cannot accurately be measured in damaged areas due to the high variability and technical stimulus range of the perimeter, it was fixed at 5%. In supplementary analyses (not shown), other fixed values (2%, 1%) were used, but this only minimally affected the results. These results therefore give the best-fit sensitivity and slope of the FOS curve under the null hypothesis that if contrast could be increased sufficiently, the observer’s response rate would eventually reach 95%.

In a secondary analysis, FN was fit as a third free parameter, constrained to be between 0% and 100%, so that 1-FN represents the asymptotic maximum response probability. This corresponds to the alternative hypothesis that the response probability could saturate at some asymptotic maximum value below 100%, rather than eventually reaching 100%. In some cases, it is possible that the fitted value of FN could be greater than 50%. This implies that the fitted asymptotic maximum probability of response is below 50%. Hence, contrast sensitivity in its most common formulation, namely the contrast to which the subject will respond on 50% of presentations, is undefined, since a response probability >50% will never be achieved no matter how high the stimulus contrast presented.

The pointwise sensitivities fit in the primary analysis represent our best estimate of the true sensitivity under the null hypothesis. These will be referred to henceforth as the “MOCS Sensitivity”. The correlation between these and the perimetric sensitivity was calculated within subgroups whose perimetric sensitivities fell within each of 35 overlapping bins, each spanning a range of 8dB, with the central values of adjacent bins separated by 0.5dB. That is, the correlation was calculated in the bin containing those locations with perimetric sensitivity 8–16dB, then the correlation in the bin containing 8.5–16.5dB, etc. The significance of the correlation was calculated using a generalized estimating equation (gee) model,³¹ to account for the fact that there could be several locations from the same subject within the bin and that the data collected from a single subject could be correlated.

Results

Data were collected from 34 subjects, comprising 20 females and 14 males. The mean age was 69.9 years (range 52 to 87). The Mean Deviation (MD) on their last clinic visit averaged − 10.90dB (range −20.94dB to −3.38dB) and the corresponding Pattern Standard Deviation (PSD) averaged 9.60dB (range 3.60dB to 14.56dB). 75 of the 136 locations tested had perimetric sensitivities ≤19dB.

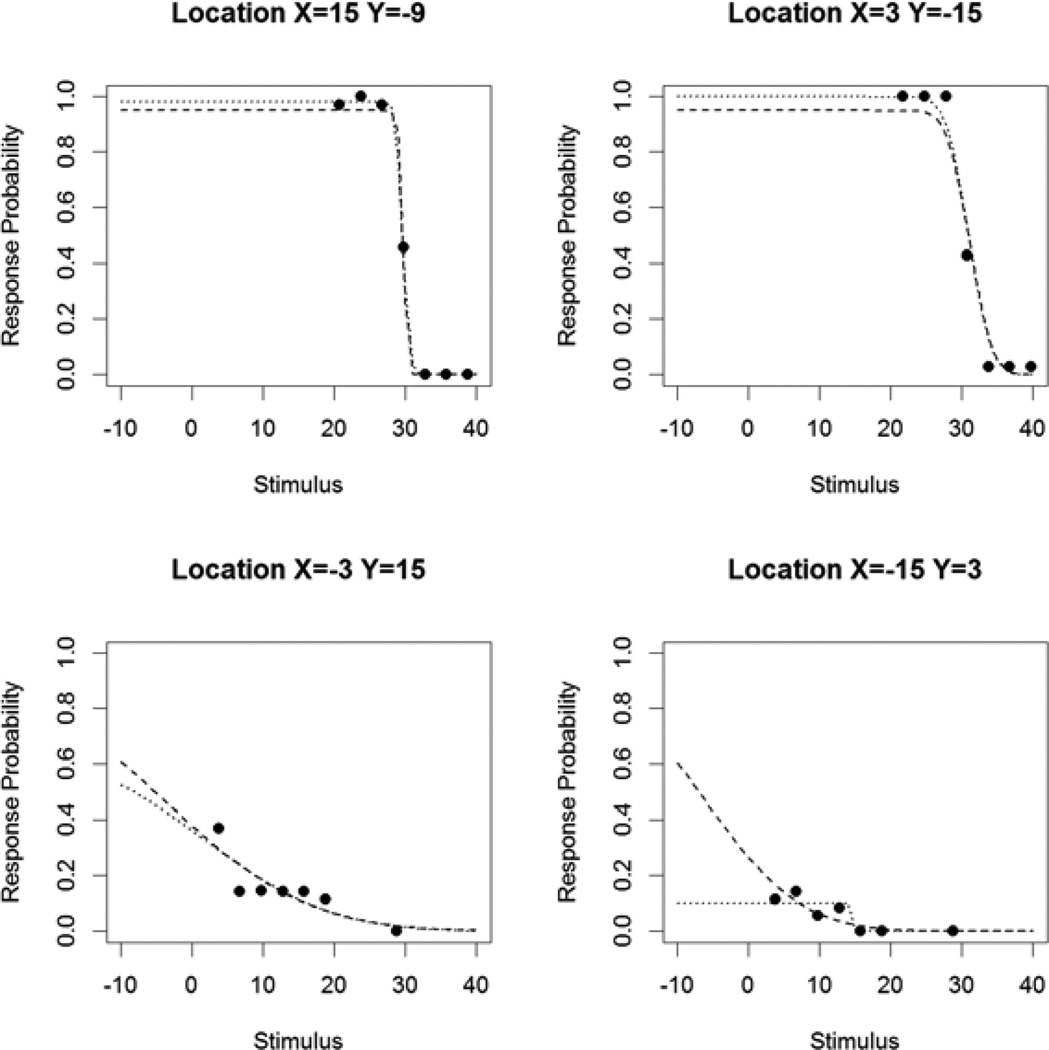
Figure 1 shows the measured response probabilities for a sample study subject, together with the fitted FOS curves when assuming that the asymptotic maximum response probability is 95% as in the primary analysis (black dashed curves), and when allowing this asymptotic maximum to vary as in the secondary analysis (black dotted curves). For the two relatively healthy locations (15°, −9°) and (3°, −15°) on the top row, the expected shape of a normal FOS curve is observed, with response probability increasing to near 100% as the contrast was increased (lower on the dB scale). The MOCS sensitivities for these locations were 29.7dB and 31.1dB respectively. However, for the two more damaged locations (−3°, 15°) and (−15°, 3°) on the bottom row, the response probability never approaches 100%, despite the fact that it is clearly greater than zero and so some function remains. The fitted sensitivities assuming a 5% false negative rate (dashed curves) are −4.1dB and −6.3dB, despite the fact that during the subject’s last clinic visit the pointwise sensitivities measured by perimetry were 15dB and 14dB respectively. In the secondary analysis allowing for response saturation (dotted curves), the fitted asymptotic maximum response probability is 66% for location (−3°, 15°) (bottom left). This indicates that unless the false negative error rate is extremely high (which seems unlikely given that the subject produces response probabilities reaching 100% at the healthier locations), response saturation is likely taking place. For location (−15°, 3°) (bottom right), the fitted asymptotic maximum response probability is just 10%. In this case, the response threshold (i.e. 50% probability of response) is never attained, and hence contrast sensitivity in its most common clinical formulation is undefined.

Figure 1.

Response probabilities for a sample study subject, at four tested locations (at positions as labeled in degrees). The dashed curve indicates the Frequency-of-Seeing (FOS) curve as fitted using the primary analysis, in which the maximum response probability would be 95% if contrast could be made sufficiently high (assuming a 5% false negative rate). The dotted curve indicates the FOS curve fit allowing this asymptotic maximum to vary, as in the secondary analysis described in the Methods section.

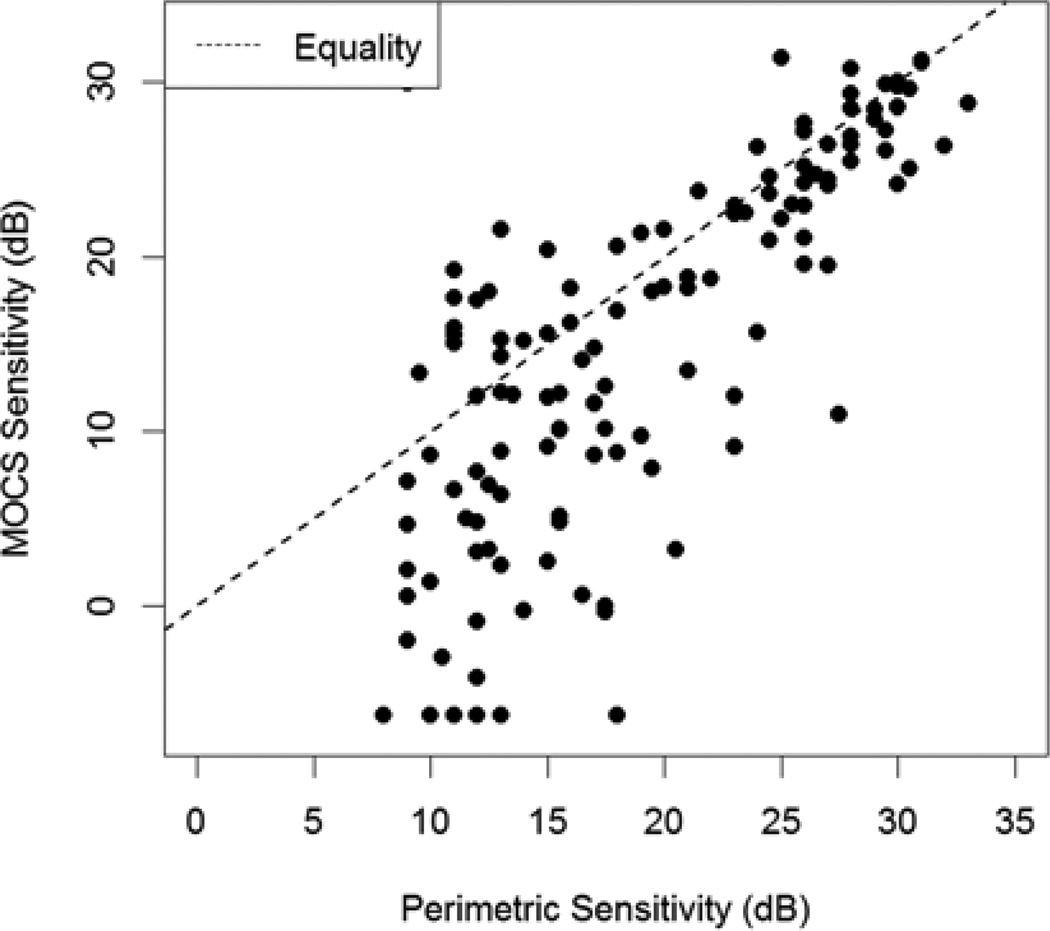
Figure 2 plots the MOCS sensitivity (fitted to the experimental data assuming a false negative rate of 5%, i.e. according to the null hypothesis) against perimetric sensitivity (the average of the sensitivities measured by perimetry at the two most recent clinic visits), for all 4 locations of all 34 subjects. At higher perimetric sensitivities, the association is quite strong, and perimetry appears to reflect the MOCS sensitivity, with a comparatively small amount of variability.

Figure 2.

Sensitivities at each location measured using the Method of Constant Stimuli (MOCS) plotted against the mean of the last two sensitivities measured in clinic using perimetry. Below around 15–19dB, the spread of the data increases markedly, and perimetry tends to overestimate the sensitivity by a seemingly random amount.

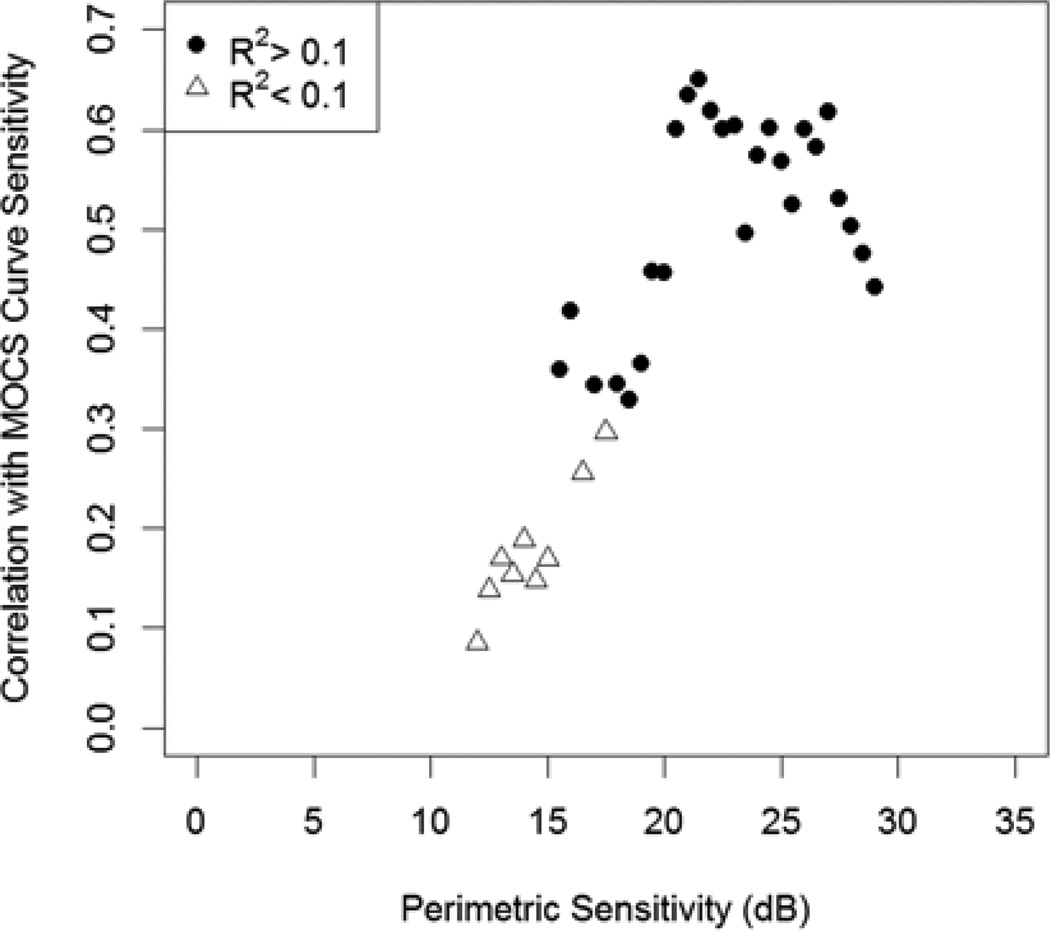
However at lower perimetric sensitivities, the association breaks down. Here, perimetry tends to overestimate the MOCS sensitivity. Perhaps more importantly, it does so by an unpredictable amount. Figure 3 shows the correlation between perimetric and MOCS sensitivities within sliding bins of width 8dB. For each bin centered at sensitivities ≥19dB (i.e. the bins covering the ranges 15–23dB, 15.5dB–23.5dB, etc.), the relation has R²>0.1 and is significant at the 5% level. At sensitivities below this level the correlation between the two is lower, and indeed is generally not even statistically significant despite sample sizes of at least 39 tested locations in each of the bins. For each bin centered at sensitivities ≤15dB, the relation has R²<0.1 and is never significant at the 5% level.

Figure 3.

The correlation between sensitivities measured accurately using the Method of Constant Stimuli (MOCS) and the mean of the last two sensitivities measured in clinic using perimetry, for the subset of locations with perimetric sensitivity within ±4dB of each center value shown. The correlations are calculated for subsets with different center values at steps of 0.5dB. Points appear as filled circles if the relation had R²>0.1.

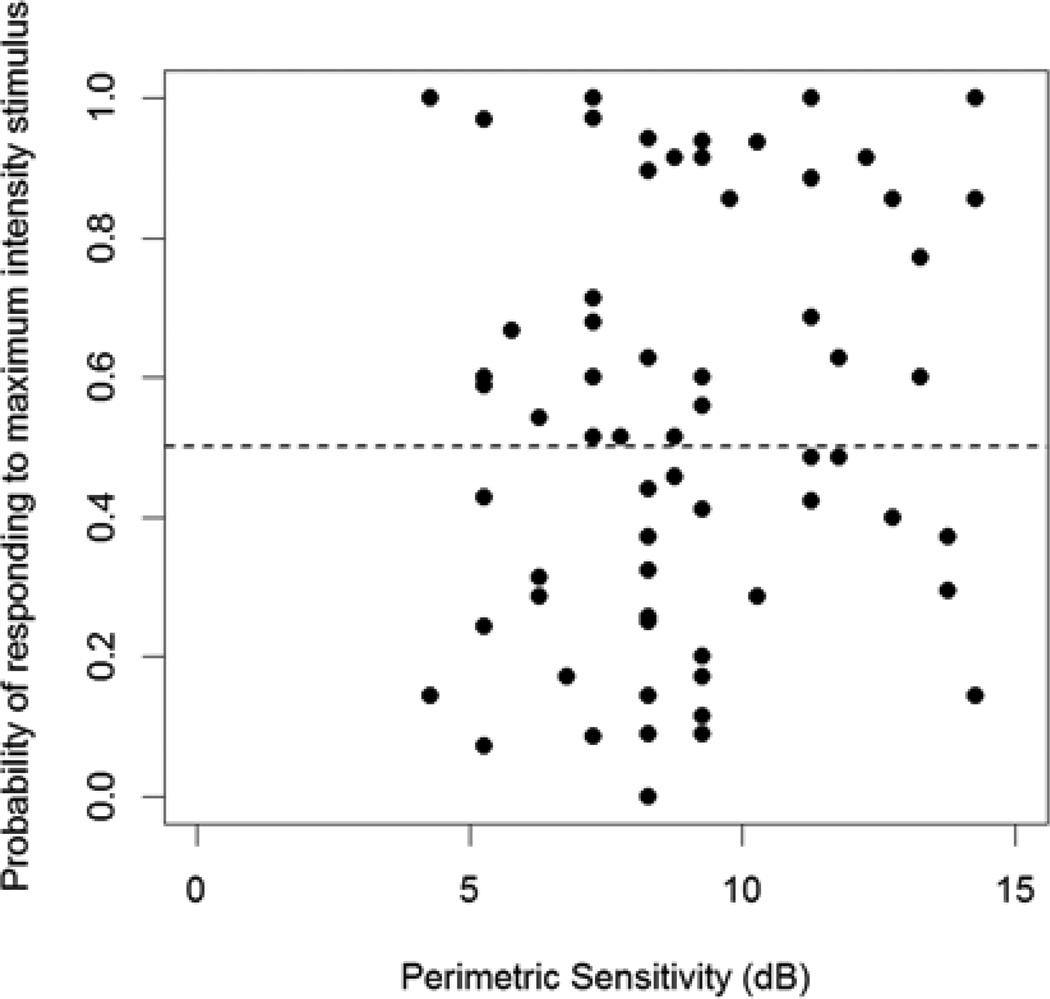
Figure 4 shows the percentage of presentations during MOCS testing for which the subject responded to the highest luminance stimulus presented, at each of the two most damaged locations (according to their perimetric sensitivity). This maximal stimulus was 0dB on the Octopus perimeter used for testing, equivalent to 3.7dB on an HFA perimeter (the units reported here). At 44% of locations, this probability was below 50%, indicating that the sensitivity is likely below 3.7dB, despite the fact that the perimetric sensitivities at these locations were at least 8dB in every case.

Figure 4.

The probability that the study subject responded to the most intense stimulus (3.7dB) at each of the two most damaged locations tested, plotted against the mean of the last two sensitivities measured in clinic using perimetry. A response probability <50% indicates that the sensitivity is likely lower than 3.7dB.

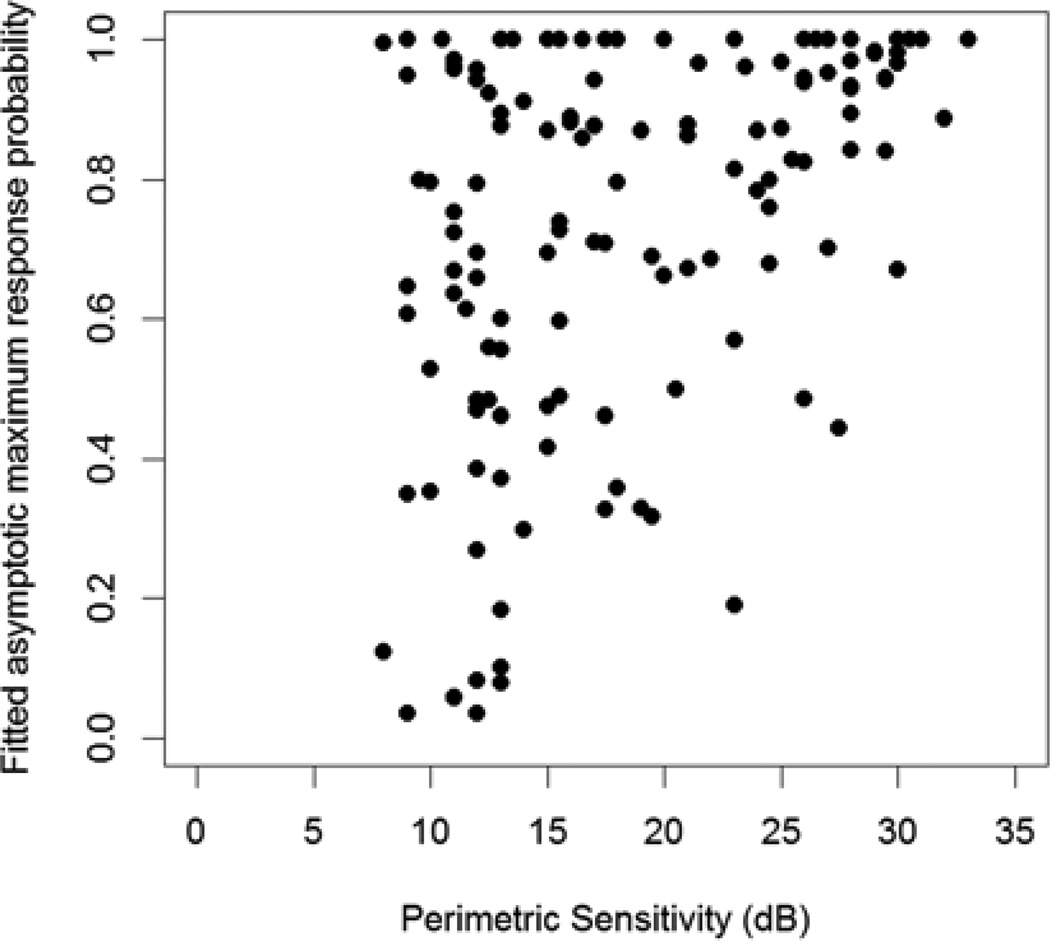
In the secondary analysis, instead of assuming as in the null hypothesis that the response probability would eventually reach 95% (100% minus the assumed false negative rate of 5%), this asymptotic maximum response probability was fit by constrained maximum likelihood estimation and allowed to take values between 0 and 100%. Figure 5 shows these fitted asymptotic maxima plotted against perimetric sensitivity. As an example, for 57 of the 81 locations (70%) with perimetric sensitivity <19dB, including 49 of the 63 locations (78%) that were ≤15dB, the asymptotic maximum response probability was below 80%. It is very unlikely that there would be more than 20% false negatives at these locations, since the subjects had fewer false negatives than this at their other locations. Therefore these results are consistent with RGC response saturation. At 30 locations the asymptotic maximum was below 50%, indicating that the commonly used threshold criterion of a 50% response rate is never attained, and so contrast sensitivity according to the conventional definition used in perimetry would be undefined.

Figure 5.

The asymptotic maximum response probability, fit as a free parameter in the maximum likelihood regression model, plotted against the mean of the last two sensitivities measured in clinic using perimetry. At low sensitivities, the response probability never approaches 100%, indicating response saturation and introducing randomness to perimetric sensitivities.

Discussion

The results in this study indicate that at most of the locations tested, the response probability did not rise appreciably with contrast beyond a cutoff. By our definition, this cutoff was between 15 and 19dB (exclusive). This could explain why the lower limit of the reliable stimulus range of standard automated perimetry might not extend to 0dB. Below 15–19dB, there was no substantial relation between the clinically-attained perimetric sensitivities and the sensitivities measured more accurately using FOS curves. Perimetric sensitivities at locations with these severities of glaucomatous damage will vary from test to test, anywhere between 0dB and 15–19dB. Change from ≥19dB to within this range, and change from within this range to <0dB (which means that no stimuli were responded to), could still indicate possible change. However, a potential implication of these results is that an apparent change in sensitivity within the range from 0dB to 15–19dB may not be informative of true disease progression. This finding has implications for many glaucoma patients with moderate to severe glaucoma, in particular those with focal defects with sensitivity worse than 19dB.

The fact that sensitivities measured using perimetry become more variable later in the disease process for glaucoma has been appreciated for some time.^{1, 7, 8, 10, 22} However, if locations with such low sensitivities are measured and the main source of variability were the slope of the FOS curve, a reliable and accurate measure of the true sensitivity could be obtained by increasing the number of presentations. The results in this study indicate that the variability could also be caused by a lowering of the asymptotic maximum response probability below 15–19dB. This means that locations with sensitivities reported as being, for example, 6dB may be indistinguishable from locations with reported sensitivity 14dB, since the asymptotic maximum has been reached, and so those locations could be considered as being effectively the same. If this is true, it would imply that any change in the threshold upon repetition is more likely due to chance than due to progression. The useful information gained by such repeated testing would be an increased confidence that the sensitivity is indeed between 0dB and 15–19dB, instead of it being a location with a threshold above 15–19dB at which the subject previously missed a stimulus presentation during testing, or a location with true threshold <0dB without any remaining function measureable using this stimulus.

This study demonstrates that some of the implicit assumptions underlying clinical perimetry may not hold true. For example, consider the location (−15°, 3°) from the subject shown in Figure 1. There is approximately a 10% probability that the observer will respond to any stimulus more intense than 15–19dB. If such a response occurs, the testing algorithm assumes that the sensitivity is almost certainly greater than this value. However, the location does not appear to have a true sensitivity greater than 0dB. According to the response saturation hypothesis, the contrast at which the subject first responds would be seemingly random within the range from 0dB to 15–19dB, and the probability of producing a ‘seen’ response would not increase substantially with contrast, except due to light scatter (which could cause a small increase in response but one that would be uninformative of the sensitivity at the location being tested). This represents a plausible explanation for the unreliability and poor repeatability of perimetric sensitivities at such damaged locations.

This interpretation of the results suggests a potential framework for assessing visual fields. Deteriorating locations in the visual field could be considered as passing through four ‘stages’. In the first ‘stage’, sensitivities from perimetry are reliable for most subjects. Even though there is some test-retest variability, the results are informative of both disease status and progression. The results shown here do not affect the interpretation of sensitivities ≥19dB. The second ‘stage’ would begin once the pointwise sensitivity has reached 15–19dB. Sensitivities reported by perimetry are no longer reliable, as the asymptotic maximum response probability is likely to be reduced introducing a substantial new source of variability. A limited amount of useful information can still be gained, principally that the sensitivity is between 0dB and 15–19dB. However, an apparent change in sensitivity from, for example, 14dB to 4dB, would not be taken as evidence of progression, since it is more likely the result of chance. The third ‘stage’ would occur once the asymptotic maximum response probability has fallen below 50%. Contrast sensitivity, in its most common formulation (as output by the perimeter), is no longer defined. However, the location still retains some function, and responses to stimuli may still occur, which would cause the perimetric sensitivity to be reported as being ≥0dB. The fourth ‘stage’ would occur once all remaining function has been lost. In this case, the sensitivity reported by perimetry should be <0dB every time. Repeated <0dB measurements therefore still provide useful information, although the possibility that there is still a low level of remaining function (i.e. the location is still within the third ‘stage’) cannot be entirely discounted. While perimetry remains useful in early and moderate disease, there may be no way to use standard automated perimetry with a static size III stimulus to assess progression within or between these second and third ‘stages’ of functional damage. It is possible that use of a larger stimulus could extend the reliable stimulus range,²¹ and a study addressing this issue is underway.

Figure 6 provides an example from a patient from the Devers Eye Institute glaucoma clinic for whom our findings could affect the clinical interpretation of the test results. Three visual fields (HFA, 24-2, SITA standard algorithm) are shown, measured approximately six months apart. In many regions of the upper hemifield, sensitivities were <19dB. Locations whose sensitivities appeared to have reduced on the second test date frequently appeared to increase again on the third test date, and vice-versa. Such changes between consecutive fields might not constitute reliable evidence of disease progression. Even at locations where there may be true progression occurring, the change in sensitivity would be overestimated if it were assumed that all sensitivities were reliable. For example, the sensitivity at location (15°, 9°) appears to fall from 21dB to 8dB over the first two visits, implying a dramatic decrease in sensitivity. However, our results indicate that the true sensitivity at the second test date could have been as high as 19dB. Indeed, on the third test the reported sensitivity at that location had increased to 17dB.

Figure 6.

An example of three visual fields from a patient attending the Devers Eye Institute glaucoma clinic, each approximately six months apart. Fields are presented in order of test date, from top to bottom. Apparent change in parts of the superior hemifield between the first two fields is unreliable, since the sensitivities are below 15–19dB, and should not be taken as evidence of glaucomatous progression. At other locations the amount of change could be overestimated.

Within glaucoma research, many studies have relied on perimetric sensitivities from severely damaged locations, which may be unreliable. Our interpretation of the results suggests restricting analyses to locations with sensitivities ≥19dB. For example, there has been debate over the best statistical models to deal with the ‘floor effect’ occurring at 0dB.^32–34 However, our findings suggest that a ‘floor’ might actually exist between 15–19dB. Studies of the structure-function relation^{35, 36} would be affected by the inclusion of regions with severe glaucomatous damage whose sensitivities are unreliable, and it remains to be seen whether this has any material impact on the conclusions. The implications of our findings on other studies will vary depending on the study population used. The Ocular Hypertension Treatment Study, for instance, consisted of subjects with visual fields that were within normal limits at baseline,³⁷ and so the proportion of locations that progressed beyond 19dB was likely small; the implications of findings from that study are unlikely to change.

Our results also suggest the possible need for alternate clinical methods for assessing progressive functional change. For example, severely damaged locations (in this case worse than 15dB) appear to be unreliable, and locations between 15dB and 19dB may also be unreliable for many patients. Future research could evaluate whether analyses to detect progression such as the Glaucoma Progression Analysis (GPA) may overcall these locations as progressed or improved. Clinicians may need to detect progression by evaluating locations with less severe loss (≥19dB), or look for evidence of damage appearing in previously normal locations. The clinical implications of these results will need to be studied further.

Our results focus on pointwise sensitivities. However, it is important to remember that if the visual field contains locations with sensitivity below 19dB, then the global indices such as Mean Deviation, Pattern Standard Deviation and the Visual Field Index will also be affected. If only one or two locations have sensitivities that are only slightly below 19dB, the effect on global indices may be minor. However if large regions of the visual field have sensitivity below 15dB, then global indices could also be unreliable, and while some of the resultant variability will average out, changes in those indices should be interpreted with caution.

In this paper, we have chosen 15–19dB as the cutoff beyond which perimetric sensitivities become unreliable. This is based on the fact that the relation between MOCS and perimetric sensitivities had R²<0.1 for all bins centered at ≤15dB, and for some of the bins between 15–19dB, indicating that less than 10% of the observed variance has been explained by differences in the true sensitivity. For research purposes, it is useful to have a fixed criterion so that data analyses can be performed. We would recommend using a cutoff of ≥19dB. However, it should be appreciated that this cutoff is not absolute. It was chosen as being the sensitivity below which the relation between MOCS and perimetric sensitivities could have R²<0.1 in our experiment, as seen in Figure 3. This criterion is useful but essentially arbitrary, and other criteria could have been chosen. For example, a statistically significant relation between MOCS and perimetric sensitivities (p<5%) was observed for all bins centered at >18dB. A different point within the bin could be chosen instead of its center. The highest perimetric sensitivity for which the probability of detecting the highest contrast stimulus ever fell below 50% was 20.5dB. Wall et al have previously defined the lower limit of the reliable stimulus range (which they referred to as the “effective dynamic range”) as being the contrast below which at least 5% of retest sensitivities were 0dB, and reported that this floor was at around 18–20dB for a size III stimulus.²¹ Notably, all of these definitions result in similar values for the cutoff beyond which standard automated perimetry with a size III stimulus may become unreliable. The results in this paper confirm and extend those previous findings, and provide a new explanation for the lack of reliability.

Perhaps more importantly, the cutoff will likely vary between locations according to eccentricity, due to changes in RGC density, peripheral refractive error,³⁸ etc. In this study, all locations tested were within the 24-2 test pattern. The locations had mean eccentricity 15.6°, ranging from 4.2° to 22.8°. At more peripheral locations than those tested here, the size III stimulus does not entirely cover the center of an RGC receptive field, which could affect the contrast at which its response becomes saturated. It is possible that age could also affect the relevant properties of RGCs. The cutoff may also vary between individuals, not only due to differences in RGC density but also due to potential reductions in the effective stimulus contrast caused by media opacities. Of the 33 eyes tested in this study, 5 had visual acuity of 20/40, while another 3 had visual acuity of 20/30 (all others were either 20/25 or 20/20). If an eye has enough forward light scatter to degrade best-corrected acuity, then this scatter will reduce the contrast of perimetric stimuli formed on the retina.³⁹ For example, the retinal contrast produced by a 16dB stimulus in an eye with substantial light scatter could be the same as the retinal contrast produced by a 20dB stimulus in an eye with clearer media, meaning that for the eye with poorer optical quality the 16dB stimulus is still within the reliable stimulus range. The lower limit of the reliable stimulus range may also be lower (in dB) in eyes with poor optical quality. In our study, there are some indications consistent with this hypothesis when analyzing subsets of the data, but we did not have a sufficiently large sample size to definitively assess the issue. This issue would likely only have a substantial effect on the results in subjects with cataract or other pathologic media opacities, for whom the lower limit of the reliable stimulus range could be even lower than 15dB, but no such subjects were included in this study. While sensitivities below 19dB did not appear to be reliable for all subjects, they will be reliable for others due to these inter-individual differences in anatomy and RGC properties. In this study there was some evidence that it may be possible to obtain reliable sensitivities using perimetry for certain individuals down to 15dB, and so we would recommend this as the floor of future testing algorithms that rely on these stimuli.

While variability has been suggested as a precursor of visual field damage in glaucoma,⁴⁰ the high variability of perimetric sensitivities has more typically been thought of as a problem to be battled, rather than a potential source of information. However, gaining an improved understanding of the reasons for this variability could aid efforts to reduce it, whether that is by post-processing of the data,⁴¹ different test algorithms,^{42, 43} or different test stimuli.⁴⁴ It may also potentially shed light on aspects of the pathophysiology such as the possible presence of living yet dysfunctional RGCs.^{45, 46} If RGCs were dysfunctional in a manner that caused a proportionately reduced response to any given stimulus contrast, this might effectively ‘shift’ the FOS curve towards the left (towards higher contrasts / lower sensitivity). Response probabilities would still eventually reach 100%, but at a greater contrast than would be the case for healthy cells. There was no evidence for this hypothesis in our results, since the response probability frequently would not reach 100% within the contrast range produced by modern increment perimeters. Our data do not rule out other forms of dysfunction. For example, the maximal response of a dysfunctional RGC could be reduced.

The inaccuracy of perimetry when assessing sensitivity at damaged locations is not caused by the choice of testing algorithm (in this case, the SITA algorithm²⁰). For many of the locations tested, the asymptotic maximum response probability was below 50%, making the contrast sensitivity in its most commonly used formulation undefined, and so reducing the effectiveness of standard automated perimetry at that location. No testing algorithm would be able to converge with low tolerance to a contrast that has 50% response probability if the response probability never actually reaches 50%. Even when the asymptotic maximum is greater than 50%, if there is only a small increase in response probability with contrast (which would be expected since RGC saturation is an asymptotic rather than absolute phenomenon), that increase is so small that a testing algorithm would require an unrealistically long test duration to reliably determine the response threshold. In this study, testing took up to half an hour to quantify performance at just four locations. Our conclusions also apply equally to different perimeters. Due to the instrument-specific nature of the dB scale, the cutoff we have chosen would be different; 19dB on the HFA (the units used in this report) is equivalent to 15.3dB on the Octopus 900 perimeter, or 400% contrast. It should be noted that the perimetric sensitivity used in this study was the mean of the two most recent clinical visual field tests, and the results if a single test had been used would most likely have been more variable than shown here.

In this study, we made every attempt to make the FOS curve testing mimic clinical perimetry as closely as possible. The most significant difference is that only four locations were tested instead of 54 (in a 24-2 visual field) or 68 (in a 10-2 visual field). This will have reduced spatial uncertainty, and this could have decreased the slopes of the FOS curves.²⁸ Testing took place as part of a longer session lasting up to an hour in total, and so some fatigue effects may be present, which could lower the MOCS sensitivity. Allowing breaks between runs should have minimized these effects, and the majority of subjects took at least one longer break of ten minutes or more part way through the testing sequence.

In summary, this study found that in eyes with glaucoma, clear media and no other ocular comorbidities, pointwise sensitivities below approximately 15–19dB from clinical perimetry showed little correlation with the true functional status at that location. In an eye with relatively clear media, the only reliable information that such locations provide may be that the sensitivity is likely to be between 0dB and 15–19dB. These findings provide a possible explanation for the high variability observed at low sensitivities when using perimetry. It may be useful to analyze data from research studies on the basis of 19dB being the lower limit of the reliable stimulus range of standard automated perimetry, rather than using the 0dB lower limit of the technical stimulus range of the instrument. Clinically, threshold values below 15–19dB should be interpreted with caution, as they may not be reliable for assessing the true level of damage or of glaucomatous progression.