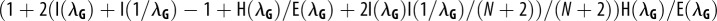Table 1.

Overview of published indices related to the concept of integration. In the definitions, N is the number of traits, λ is the eigenvalues of the correlation matrix, r is the set of pairwise correlation coefficients, E denotes the expectation (the average) and |x| denotes the absolute value of x.

index	notes	references
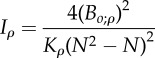	a complex index related to the fraction of correlations above a fixed threshold, and scaled to lie between 0 and 1a	Olson & Miller [5]
Iz = tanh(E(|z|))	average of Fisher's z-transformed correlation back transformed to 0–1 scaleb	Van Valen [32]
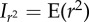	average coefficient of determination, estimated as the mean of the squared pairwise correlations	Van Valen [159]
Ir = E(|r|)	average of the absolute pairwise correlations	Cane [160]
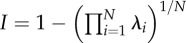	one minus the geometric mean of the correlation-matrix eigenvalues	Cheverud et al. [161]
var(λ)	variance of the correlation-matrix eigenvalues	Wagner [162], Cheverud et al. [163]
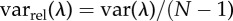	relative variance of the correlation-matrix eigenvalues; the value N − 1 is the maximum possible variance of an eigenvalue	Pavlicev et al. [164]
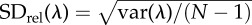	relative standard deviation of the correlation-matrix eigenvalues	Cheverud et al. [161], Pavlicev et al. [164]
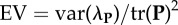	the variance of the variance-matrix eigenvalues (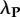) scaled by the total variancec	Young [165], Willmore et al. [166]
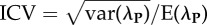	the standard deviation of the variance-matrix eigenvalues scaled by the mean of the eigenvalues	Shirai & Marroig [167]
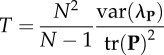	one of Van Valen's [159] measures of ‘tightness’, the closeness of the distribution to the major axis, varying between 0 and 1	Van Valen [159]
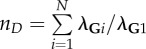	the sum of the genetic variance matrix eigenvalues (λG) scaled by the leading eigenvalue (λG1)	Kirkpatrick [168]
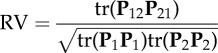	a measure of the total amount of covariation between the two sets of variables over a measure of the total amount of variation in the within the two groupsd	Klingenberg [98]
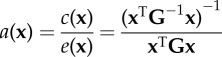	the fraction of independent additive genetic variation (autonomy) for a particular linear combination of the traits (x)e	Hansen & Houle [169]
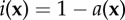	the fraction of non-independent additive genetic variation (integration) in the direction of x	Hansen & Houle [169]
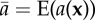	the average autonomy of uniformly distributed random directionsf	Hansen & Houle [169]
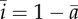	the average integration of uniformly distributed random directions	Hansen & Houle [169]

^aB_o;ρ is number of correlations above, or equal to, the lower statistical significance level (a function of sample size) of a fixed arbitrary threshold correlation given by ρ. K_ρ is the number of non-contained ρ-groups, where non-contained means the largest group which can be formed where all elements have pairwise correlations ≥ ρ.

^btanh is the inverse Fisher transformation (the hyperbolic tangent), z is a set of Fisher's z-transformed pairwise correlation coefficients.

^ctr is the trace function. P is the phenotypic variance matrix.

^dP₁, P₂, P₁₂ and P₂₁ are the sub matrices of a phenotypic variance matrix. The sub matrices P₁ and P₂ are the variance matrices for the two sets of traits, respectively. The sub matrices P₁₂ and P₂₁ are the covariances between the two sets of traits.

^ee(x) is the evolvability and c(x) the conditional evolvability along a unit length vector (or direction) of the traits x, G is the additive genetic covariance matrix, ^T denotes the transpose, and ⁻¹ denotes the inverse. To calculate the autonomy to a specific trait with respect to the rest, we can use a vector x with the coefficient 1 for the focal trait and zero for the rest. The different indices from Hansen & Houle [169] are easily computed using the R package ‘evolvability’ (see [156]).

^fThis can be approximated by , where H(λ) ≡ 1/E(1/λ) is the harmonic mean, and I(λ) ≡ var(λ)/E(λ)² is the mean-standardized variance. The average autonomy can alternatively be measured as the average of the individual trait autonomies (see [90,114]).