Table 4. Comparison of various differentiation measures for Matrix I (with 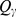 = 0.48,  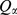= 0.47) and Matrix II (with  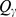= 0.167,  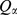= 0.102) based on abundance and function (A&F), on function (F) only, and abundance (A) only.

Measure	Order	Matrix I			Matrix II
		A&F	F	A #	A&F	F	A #
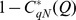
	q = 0	0.324	0.324	0.4	0.579	0.579	0.4
	q = 1	0.408	---	0.4	0.628	---	0.4
	q = 2	0.491	---	0.4	0.678	---	0.4
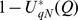
	q = 0	0.657	0.657	0.571	0.846	0.846	0.571
	q = 1	0.408	---	0.4	0.628	---	0.4
	q = 2	0.194	---	0.25	0.345	---	0.25
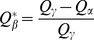
	q = 2	0.002			0.388
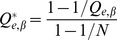
	q = 2	0.004			0.145
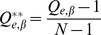
	q = 2	0.002			0.078

^#Differentiation measures are the abundance-based local differentiation measure (1−C_qN) and regional differentiation measure (1−U_qN) obtained from partitioning Hill numbers [36];

--- No measures for q = 1 and q = 2 because species abundances are not considered for measures based on function (F) only.