Table 6. Comparison of various differentiation measures for three pairs of habitats in the real data analysis based on abundance and function (A&F), on function (F) only, and abundance (A) only.
| Measure | Order | EM vs. MO | EM vs. TR | MO vs. TR | ||||||
| A&F | F | A # | A&F | F | A # | A&F | F | A # | ||
|
q = 0 | 0.316 | 0.316 | 0.392 | 0.375 | 0.375 | 0.457 | 0.043 | 0.043 | 0.062 |
| q = 1 | 0.428 | --- | 0.427 | 0.714 | --- | 0.721 | 0.282 | --- | 0.278 | |
| q = 2 | 0.658 | --- | 0.573 | 0.885 | --- | 0.854 | 0.539 | --- | 0.457 | |
|
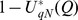
q = 0 | 0.649 | 0.649 | 0.564 | 0.706 | 0.706 | 0.628 | 0.152 | 0.152 | 0.118 |
| q = 1 | 0.428 | --- | 0.427 | 0.714 | --- | 0.721 | 0.282 | --- | 0.278 | |
| q = 2 | 0.324 | --- | 0.401 | 0.659 | --- | 0.746 | 0.226 | --- | 0.296 | |
|
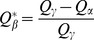
q = 2 | 0.028 | 0.042 | 0.026 | ||||||
|
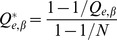
q = 2 | 0.066 | 0.102 | 0.067 | ||||||
|
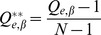
q = 2 | 0.034 | 0.054 | 0.035 | ||||||
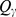= 0.550 and 
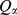= 0.535 for the pair (EM, MO); 
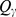= 0.561, 
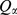= 0.537 for the pair (EM, TR); 
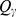= 0.574, 
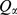= 0.559 for the pair (MO, TR).
#
Differentiation measures are the abundance-based local differentiation measure (1−CqN) and regional differentiation measure (1−UqN) obtained from partitioning Hill numbers [36];
--- No measures for q = 1 and q = 2 because species abundances are not considered for measures based on function (F) only.