Figure 1. Opinions described via Gaussian densities (17).
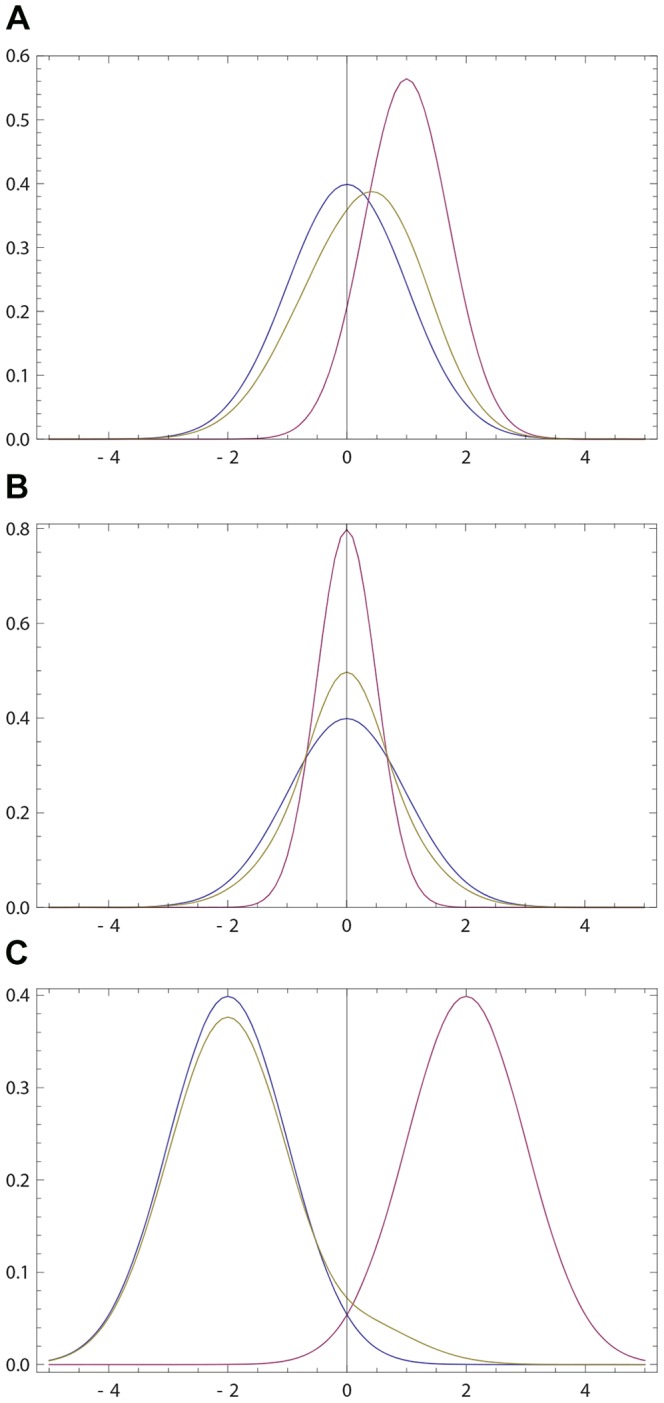
The initial opinion of 
is described by Gaussian probability density p(x) (blue curve) centered at zero; see (17). The opinion of 
amounts to Gaussian probability density q(x) (purple curve) centered at a positive value. For all three figures continuous density f(x) (
) were approximated by 100 points 
, 
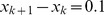. The resulting opinion 
of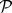 
is given by (16) with 
(olive curve). (a) The opinion of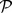 
moves towards that of 
; 
, 
, 
, 
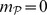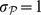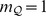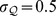. (b) The maximally probable opinion of 
is reinforced;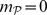 
, 
, 
, 
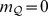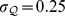. (c) The change of the opinion of 
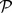is relatively small provided that the Gaussian densities overlap only in the region of non-commitment; cf. (18), (19). Whenever the densities overlap only within the rejection range the difference between p(x) and 
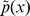is not visible by eyes. For example, if p(x) and q(x) are Gaussian with, respectively, 
, 
, 
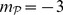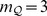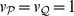, the Hellinger distance (see (30) for definition) 
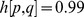is close to maximally far, while the opinion change is small: 
.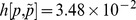