Figure 3. Opinion change versus discrepancy.
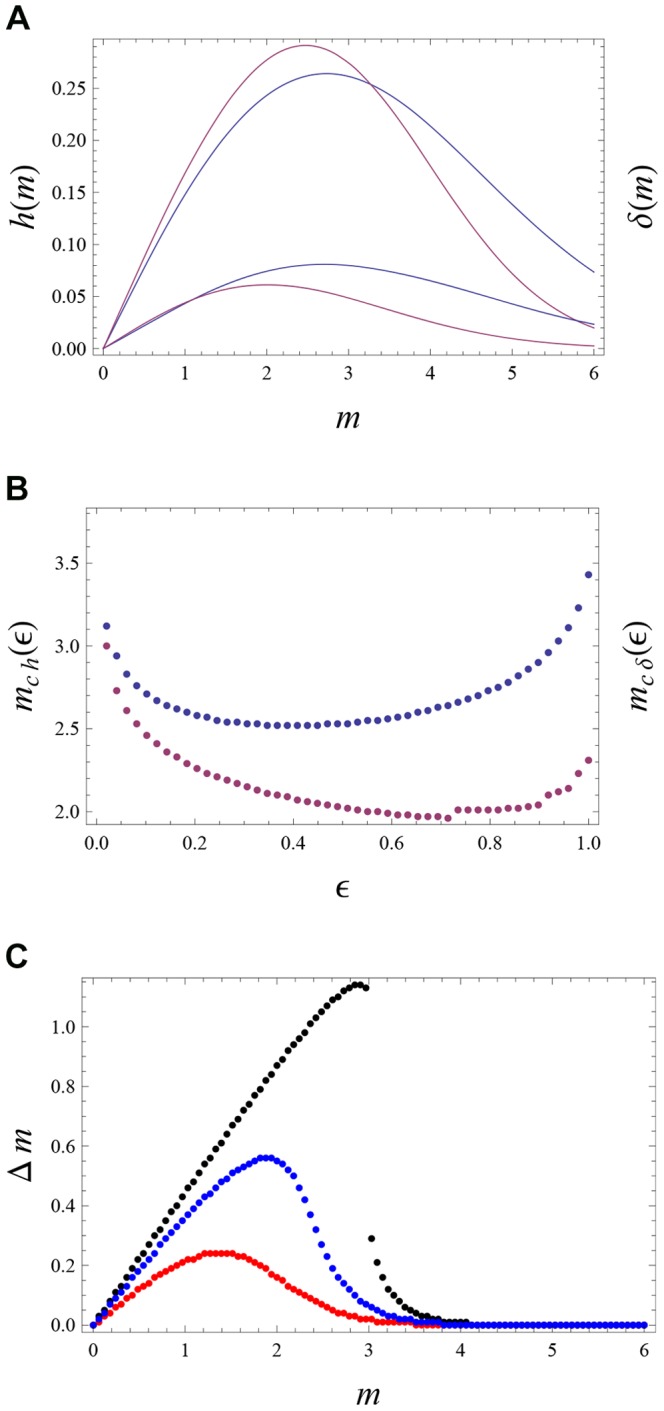
(a) The opinion change is quantified via the Hellinger distance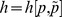 
between the old and new opinion of 
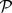(blue curves); see (30) for the definition. For comparison we also include the total variance distance 
(purple curves); see (33). These two distances are plotted versus the discrepancy 
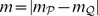. The initial opinion of the agent 
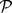is Gaussian with 
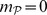and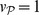 
; see (17). The opinion of 
is Gaussian with 
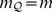and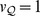 
. Thus m quantifies the initial distance between the opinions of 
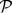and 
. The final opinion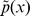 
is given by (13). Different curves correspond to different 
. Blue curves: 
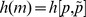for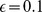 
(upper curve) and 
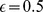(lower curve). Purple curves: 
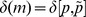for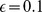 
(upper curve) and 
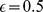(lower curve). The maximum of h(m) (
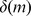) is reached at 
(
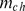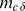). (b) 
(
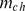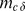) is the point where h(m) (
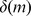) achieves its maximum as a function of m. Blues points: 
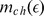versus 
for same parameters as in (a).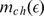 
grows both for 
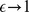and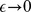 
, e.g. 
, 
, 
, 
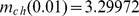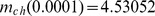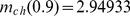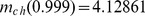. Purple points: 
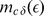versus 
for same parameters as in (a). (c) The difference of the anchors (maximally probable values)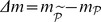 
versus 
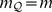for the initial opinions of 
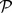and 
given by (17) under 
, 
, 
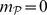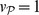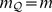and 
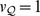. The final opinion 
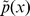of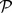 
(and its maximally probable value 
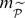) if found from (13) under 
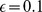(black points), 
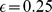(blue points) and 
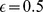(red points).