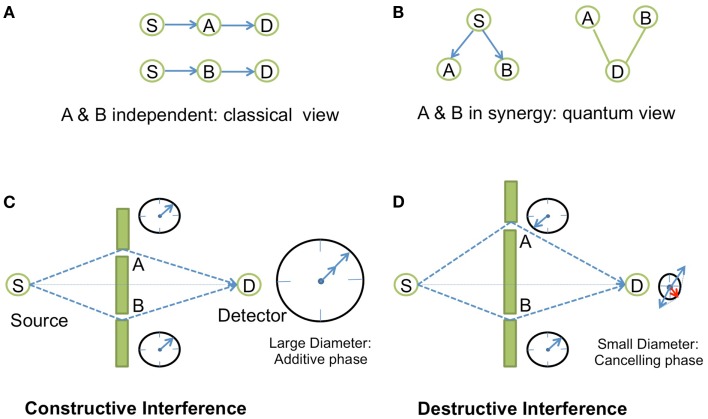
Figure 1.

Synergistic effects in Young’s interference experiment. In Young’s experiment, a source S sends photons to a detector D that is located behind a wall with two tiny slots A and B on each side of the line between S and D. (A) When the two slots A and B are independent (by disconnecting the entanglement in measuring the photons emerging from one slot with a detector behind A or B), there is no interference, and the distribution of photons on the z-direction of the screen is just Gaussian. This is the classical view of the experiment. (B) In quantum view, using amplitude of probability, the photon emerging from S and going to D has two alternating ways: slot A or slot B. The probability of the total event is the square of the amplitude of probability given by the sum of the two amplitudes for each alternating event Prob(S–D) = |⟨S–A–D⟩ + ⟨S−B−D⟩|², where ⟨.⟩ is the amplitude of probability of the event. (C) The probability of the total event will correspond to an amplified synergistic effect if the two arrows of the two independent events points toward the same direction, i.e., if the photons are in phase between each other which occurs when the difference between the two trajectories corresponds exactly to an integer number of time period difference between the two photons. This is symbolically represented by a “watch clock” for each photon that turns with a specific speed depending upon the frequency of the light. If the arrows of these two watches point toward the same direction, then the photons are in phase, and we get constructive interferences. (D) Destructive interference is observed when the arrows are in the opposite direction (opposite phase).