Multi-resolutional shape features via non-Euclidean wavelets: Applications to statistical analysis of cortical thickness

Abstract

Statistical analysis on arbitrary surface meshes such as the cortical surface is an important approach to understanding brain diseases such as Alzheimer’s disease (AD). Surface analysis may be able to identify specific cortical patterns that relate to certain disease characteristics or exhibit differences between groups. Our goal in this paper is to make group analysis of signals on surfaces more sensitive. To do this, we derive multi-scale shape descriptors that characterize the signal around each mesh vertex, i.e., its local context, at varying levels of resolution. In order to define such a shape descriptor, we make use of recent results from harmonic analysis that extend traditional continuous wavelet theory from the Euclidean to a non-Euclidean setting (i.e., a graph, mesh or network). Using this descriptor, we conduct experiments on two different datasets, the Alzheimer’s Disease NeuroImaging Initiative (ADNI) data and images acquired at the Wisconsin Alzheimer’s Disease Research Center (W-ADRC), focusing on individuals labeled as having Alzheimer’s disease (AD), mild cognitive impairment (MCI) and healthy controls. In particular, we contrast traditional univariate methods with our multi-resolution approach which show increased sensitivity and improved statistical power to detect a group-level effects. We also provide an open source implementation.

Introduction

The cerebral cortex is a layer of highly convoluted surface of gray matter with spatially varying thickness, and the distance between inner and outer cortical surface is known as the cortical thickness, see Fig. 1. Within the last decade, numerous studies have shown how cortical thickness is an important biomarker for brain development and disorders — the existing literature ties this measure to brain growth (Lemaitre et al., 2012; O’Donnell et al., 2005; Shaw et al., 2006a; Sowell et al., 2004), autism (Chung et al., 2005), attention-deficit (Shaw et al., 2006b), genetic influences (Panizzon et al., 2009), amusia (Hyde et al., 2007), osteoporosis (Hodsman et al., 2000), and even gender Sowell et al., 2007. Changes in the cortical thickness (Newman et al., 1998; Prevrhal et al., 1999) are particularly important in the context of Alzheimer’s Disease (AD) (de Leon et al., 1989; Erkinjuntti et al., 1987; Pachauri et al., 2011; Thompson et al., 2004), which will be the primary focus of analysis in this paper. In this context, studies have observed significant cortical thinning in temporal, orbitofrontal and parietal regions (Lerch et al., 2005; Thompson et al., 2004) in patients with AD. Lehmann et al. (2011) used both voxel-based morphometry (VBM) and cortical thickness (CT) measures extracted by Freesurfer to find significant patterns of variation between clinical populations including AD and the related posterior cortex atrophy (PCA) group. They found cortical thinning in the occipital and posterior parietal lobe in the PCA population, and in medial temporal regions in the AD population. Similar results were found in Thompson et al. (2011) and Wirth et al. (2013) which related it to other biomarkers also. In many other AD studies, researchers have used cortical thickness as a biomarker to detect and classify AD cohorts from control subjects (Cho et al., 2012; Dickerson and Wolk, 2012; Lerch et al., 2008; Querbes et al., 2009; Wolz et al., 2011).

Fig. 1.

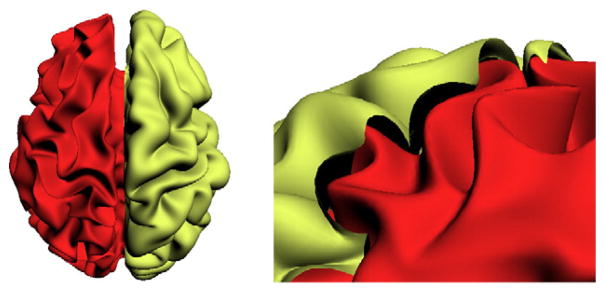
Illustration of cortical thickness. The inner cortical surface (red) is covered by the outer cortical surface (yellow), and the cortical thickness is measured by the distance between the outer and the inner cortical surfaces.

The body of work above relating cortical thickness to cognitive decline is vast and tackles various neuroscientific questions; but these studies share a commonality in that once the thickness measurement on the cortical mesh has been calculated via a pre-processing method, the main interest is to employ statistical hypothesis testing to find regions that exhibit statistically significant differences between the two groups — typically a clinic group and a control group — while accounting for various confounds. But this workflow must take into account a few potential pitfalls. The first order requirement, clearly, is to recruit a sufficient number of subjects to ensure that the study has sufficient power. Now, if the expected variations are small, the cohort size must be large enough to ensure that we can reliably identify group-wise differences. However, in many cases this is not feasible due to cost and/ or the specific scope of the clinical question of interest (demographic requirements, genetic profile etc). Therefore, it is imperative that the analysis procedure we choose is sensitive and maximizes the likelihood of detecting signal variations between the groups. Otherwise, in the small sample size regime, it is entirely possible that we will fail to discover an otherwise real disease-specific effect. Notice that analysis of two very distinct groups that lie at the opposite sides of the disease spectrum will obviously yield a strong statistical signal. But recent work, with good reason, has almost entirely focused on detecting biomarkers pertaining to the early stages of decline (Johnson et al., 2011), or on finer gradations of the clinical spectrum from control to AD. Because of the more moderate effect size in this regime, even in larger studies, identifying group differences may be challenging. Our interest then is in deriving representation schemes for the data, which helps the downstream statistical test pick up subtle group differences with higher confidence than would be possible otherwise.

Multiple comparisons

Consider the standard pipeline for analyzing cortical thickness variations in a neuroimaging study. Here, the data are defined on an intricate mesh domain (i.e., brain surface), and as a result the number of vertices needed to represent the surface (and consequently, the number of hypothesis tests) grows up to 100,000 or more. After vertex correspondences between subjects have been found, the hypothesis test is performed at each cortical surface mesh vertex. Finally, one must perform a Bonferroni or other multiple comparison correction, such as FDR or the method detailed in (Van De Ville et al., 2004). We can then conclude that the cortical regions which correspond to the surviving vertices are indeed meaningful disease-relevant regions.

Observe that in such a vertex-wise statistical task on a surface domain, improved sensitivity can be achieved by increasing the signal to noise ratio. One option may be to utilize a filtering operation (such as Gaussian smoothing). But this relies on achieving a delicate tradeoff between smoothing the signal just enough to suppress noise but taking care not to blur out the signal of interest. Instead, our key idea is to derive a descriptor for each mesh vertex that characterizes its local context, at multiple scales (or resolutions) concurrently. Such multi-resolution ideas, historically studied within image processing as scale space theory (Lindeberg, 1993) or via the Wavelet transform (Daubechies, 1990; Mallat, 1989), have been used sparingly within the context of statistical analysis on arbitrary meshes. The framework presented here gives an end to end solution that makes these ideas implementable for cortical surface data, with improved sensitivity.

Recall that the Wavelet transformation, the obvious choice for multi-resolution analysis of the form alluded to above, uses a centered oscillating function as the basis instead of the sine basis. Therefore, it overcomes the key limitation of Fourier series in failing to capture sharp changes in a function (i.e., Gibbs phenomena due to infinite support) via the localization property. Unfortunately, the conventional formulation is defined only in the Euclidean space (e.g., a regular lattice). This is not suitable for convoluted and arbitrary surface models where the mesh has a highly irregular geometry. In order to still make use of the main theoretical constructs, but in the non-Euclidean setting, one must first decide a priori a “standard” coordinate system. Popular parameterization techniques use a unit sphere and utilize the spherical harmonics (SPHARM) (Chung et al., 2007). SPHARM defines Fourier bases using spherical Laplacian to parameterize a function mapped to a sphere. This must involve a module which will ‘balloon’ out the cortical surface on to a sphere while preserving, to the extent possible, local distances, areas or angles. This is usually a lossy or distortion prone process. Based on similar ideas, the spherical wavelet defines the wavelet on a template sphere with discretized regular lattice (Antoine et al., 2002; Freeden and Windheuser, 1996). Some studies have shown how spherical wavelets can be used to analyze complex cortical surface development (Yu et al., 2007). But spherical wavelets, like spherical harmonics, by design, cannot compensate for the metric distortion already introduced in the sphere mapping module. Of course, there are some heuristic adjustments which offer varying levels of empirical performance in practice. But theoretically, it will be satisfying to remove the restriction of a standardized coordinate system completely, and derive a multi-resolution representation in the native domain itself. Experimentally, we will show that this strategy yields substantial improvements.

By leveraging some recent results from the harmonic analysis literature (Hammond et al., 2011), this paper proposes a framework to decompose a scalar function defined at each vertex of a surface model into multiple scales using non-Euclidean Wavelets. It is easy to think of this process as viewing each mesh vertex zoomed at various levels, and characterizing the set or union of all such views within a vertex descriptor. Once such a representation is derived, we can simply analyze the multi-scale signal using multi-variate statistical tests. This paper makes the case that the performance of many cortical thickness analysis studies can be significantly improved, with little additional work (of the form described above).

The main contributions of this paper² are the following:

1. We derive a highly sensitive multi-resolutional shape descriptor for performing group analysis in a population of subjects on signals defined on surfaces/shapes;

2. We demonstrate the utility of the framework on two distinct Alzheimer’s disease (AD) datasets and show rather significant performance improvements over the standard baseline. These experiments give strong evidence that a large number of cortical thickness analysis studies can immediately benefit from these ideas with negligible additional cost;

3. To facilitate adoption, we provide a toolbox implementing the framework. Our code is designed to operate directly on Freesurfer generated files and will be available on NITRC concurrently with the paper’s publication.

Preliminaries: continuous wavelet transform in the Euclidean space

To keep this paper self contained, this section briefly reviews Wavelets in the form common in introductory image processing classes. Readers familiar with this content can skip ahead.

The wavelet transform is conceptually similar to the Fourier transform in that it decomposes a given signal into a linear combination of oscillating basis functions, thereby facilitating frequency analysis. Even though the Fourier and wavelet transforms are similar, the critical difference comes from the shape of the basis functions. While the sine and cosine functions have infinite duration, that is, they are infinite repetitions of the same wave function per period, the wavelet bases provide a compact support that is localized at a specific position. The locality of the bases forms an important property of wavelet — while the Fourier transform is localized in frequency only, wavelets can be localized in both time and frequency (Mallat, 1989), and this behavior basically frees the transformation from ringing artifacts.

The conventional construction of the wavelet transform is defined by the choice of a mother wavelet ψ, and a related “scaling function” ϕ. The wavelet basis set is generated by parameterizing ψ by scales s ∈ S and translations a ∈ A:

$${\psi }_{s,a}(x)={\mid s\mid }^{-2}\psi \left(\frac{x-a}{s}\right).$$ (1)

Controlling s changes the dilation of the wavelet and changing a varies the translation of the wavelet. The wavelet transform of a signal f(x) is defined by the inner product of f and the bases function ψ as

$$W_f(s,a)=\frac{1}{s}\int f(x){\psi }^{\ast }\left(\frac{x-a}{s}\right)\mathrm{d}x$$ (2)

where ψ^* is the complex conjugate of ψ, and results in wavelet coefficient W_f(s,a). If this transformation satisfies the admissibility condition,

$$C_{\psi }=\int \frac{{\mid \widehat{\psi }(j\omega )\mid }^2}{\omega }\mathrm{d}\omega <\infty$$ (3)

where C_ψ is the admissibility condition constant and β̂(jω) = ∫ψ(x)e^−jωx dx is the Fourier transform of the mother wavelet with imaginary component. Such a wavelet transform is invertible, and the inverse wavelet transformation reconstructs the original signal f from W_f(s,a) without any loss of information as,

$$f(x)=\frac{1}{C_{\psi }}\int \int W_f(s,a){\psi }_{s,a}(x)\mathrm{d}a\mathrm{d}s$$ (4)

Here, (4) is known as resolution of the identity and the key expression for multi-resolutional analysis using the wavelet transform.

Remarks

Wavelet transform in the Euclidean space has been extensively used in image processing (Mallat, 1989, 1999). Formalizing wavelets in a non-Euclidean space such as a graph, however, is not straightforward due to the non-regularity of the domain. The next few sections provide additional detail on these difficulties and then describe our main strategy.

Non-Euclidean wavelets and a multi-resolution mesh descriptor

Extending wavelets to the non-Euclidean setting, particularly to graphs, requires deriving a representation of a function/signal defined on localized vertices, in a sense which will become clear shortly. The first bottleneck is to come up with notions of scale and translation on the graph. Briefly, the key idea motivated directly by recent results in harmonic analysis (Coifman and Maggioni, 2006; Hammond et al., 2011) is as follows. Instead of defining a wavelet function in the original space, one can define a mother wavelet in the frequency domain as band-pass filters where scale turns out to be easier to define. Transforming it back yields the wavelet in the original domain which can be localized by applying a delta function δ(n) on vertex n. To do this, an analog of Fourier transform is required between the space of the graph and the frequency space. Relying on spectral graph theory (Chung, 1997), we obtain the necessary bases to define graph Fourier transform, and then the spectral graph wavelet transform (SGWT) (Hammond et al., 2011) is derived using the graph Fourier transform. Finally, using SGWT, we construct a wavelet multi-scale descriptor, which is a multi-resolutional shape descriptor characterizing the shape/signal context at each vertex at multiple resolutions.

The following section includes common notations in graph theory (which are defined in Appendix A for completeness).

Graph Fourier transform

The spectrum of the graph Laplacian L forms a domain that provides information about the key properties and geometry of the original graph. Defining a transformation using the eigenfunctions χ_l as bases, the eigenvalues λ_l form a domain which is analogous to the frequency domain for the Euclidean space, ℝⁿ. Since eigenvectors of a self-adjoint operator, including the Laplacian, form an orthonormal basis, the bases from spectral graph theory are sufficient to form the bases for the graph Fourier transform. Using these completely orthonormal bases, the forward and inverse graph Fourier transformations of a function f(n) are defined as,

$$\widehat{f}(l)=<{\chi }_l,f>=\sum _{n=1}^N{\chi }_l^{\ast }(n)f(n),$$ (5)

$$f(n)=\sum _{l=0}^{N-1}\widehat{f}(l){\chi }_l(n)$$ (6)

where f̂ is the function in the frequency domain and N is the number of vertices. Note that these formulations are analogous to the formulations of Fourier transform, except that it uses different bases.

Wavelet transformation on graphs

Wavelets are known to serve as band-pass filters in the frequency domain. Choosing a certain type of band-pass filter function g determines the shape of the mother wavelet ψ, and from multiple scales s of the filter in the frequency domain, one can obtain the wavelet function with control over dilation in the original graph domain. This is critical to the construction, and can be achieved simply by defining an operator T_g = g(L) that acts on the function defined on each vertex of a graph. Using the graph Fourier transform,

$$T_{g}f(m)=\sum _{l=0}^{N-1}g({\lambda }_l)\widehat{f}(l){\chi }_l(m).$$ (7)

Furthermore, applying an impulse function δ(n) will localize the wavelet to be centered at a certain point n. Using these parameters, filtering operation on a impulse function by g in the frequency domain defines a wavelet function at scale s defined on vertex m in the graph domain as,

$${\psi }_{s,n}(m)=T_g^s\delta (n)=\sum _{l=0}^{N-1}g(s{\lambda }_l){\chi }^{\ast }(n){\chi }_l(m)$$ (8)

This representation of ψ can be understood from the inverse Fourier transformation, where the defined band-pass filter is realized in the original graph domain by the inverse transformation. Similar to the definition of traditional wavelet transform, the transformation is defined by the inner product of a signal f and wavelet basis function ψ as,

$$W_f(s,n)=<{\psi }_{s,n},f>=\sum _{l=0}^{N-1}g(s{\lambda }_l)\widehat{f}(l){\chi }_l(n)$$ (9)

which results in wavelet coefficients and is known as the recently proposed spectral graph wavelet transform (SGWT) (Hammond et al., 2011). Note that this expression (9) corresponds to the continuous wavelet transformation as shown in Eq. (2) with an integral of a set of coefficients and given bases. If the kernel g satisfies the admissibility condition,

$$C_g={\int }_0^{\infty }\frac{g^2(x)}{x}\mathrm{d}x\le \infty$$ (10)

and g(0) = 0, then such a transform is invertible,

$$f(m)=\frac{1}{C_g}\sum _{n=1}^N{\int }_0^{\infty }{W}_f(s,n){\psi }_{s,n}(m)\frac{\mathrm{d}s}{s}$$ (11)

which represents the original signal by superposition of wavelet coefficients and wavelet bases over the full set of scales. Eq. (11) is equivalent to the following expression (where we use χ_l),

$$\frac{1}{C_g}\sum _{l=0}^{N-1}\left({\int }_0^{\infty }\frac{g^2(s{\lambda }_l)}{s}\mathrm{d}s\right)\widehat{f}(l){\chi }_l(m).$$ (12)

Eq. (11) also corresponds to the inverse wavelet transform in the continuous setting given in Eq. (4), which completes the connection of wavelets in continuous space and SGWT.

A few examples of wavelets on graphs are shown in Fig. 2, where a triangular mesh surface is considered as the original graph domain — each node of a triangle is the vertex and each segment is considered as an edge. On the mesh surface, localized Mexican hat wavelets at different scales (dilation) are shown. If the domain were to satisfy the axioms of Euclidean geometry (i.e., a regular lattice), the wavelet functions would also form a symmetric shape. But due to the irregularity in shape of the domain, we can see that the shape of each wavelet is determined by the intrinsic geometry of the graph domain. Intuitively, we can consider the wavelet function as a unit energy localized at a vertex, and its propagation to its nearby vertices as a form of wave at different scales.

Fig. 2.

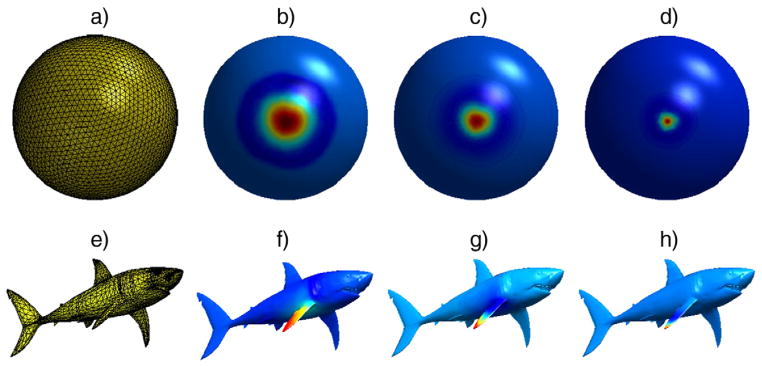
An example of Mexican-hat wavelet on a sphere and a shark shaped mesh surfaces. The range of λ from L of a sphere mesh was split into 5 different scales, and the mother wavelet ψ was built upon those scales. The wavelet is localized at one vertex (i.e., vertex index 1). As the scale varies, the dilation of the wavelet changes. a) A 3-D triangular mesh domain (sphere) with 2562 vertices and 5120 faces, b) ψ_1,1, c) ψ_2,1, d) ψ_3,1, e) A 3-D triangular mesh domain (shark) with 2860 vertices and 5716 faces, f) localized ψ_1,1 at the tip of a fin, g) localized ψ_2,1 at the tip of a fin, h) localized ψ_3,1 at the tip of a fin.

Wavelet multiscale descriptor

Similar to Fourier analysis, wavelet analysis transforms a function defined in a non-Euclidean space into an alternative basis in order to facilitate certain types of analysis. In the case of spectral graph wavelet analysis, this basis is derived from the eigen-spectrum of the graph Laplacian. The central observation underpinning this work is that such a transform would greatly facilitate statistical parametric mapping analyses of neuroimaging data. To this end, taking the spectral wavelet transform yields the wavelet multiscale descriptor (WMD). Here, we define the WMD as a set of wavelet coefficients at each vertex n for each scale in S = {s₀,s₁,…,s_{|S| − 1}}, where s₀ denotes the scaling function.

$${\text{WMD}}_f(n)=\left\{W_f(s,n)\mid s\in S\right\}$$ (13)

The WMD on each vertex n can be interpreted as the original univariate (i.e., cortical thickness,) signal being decomposed into various resolutions depending on the geometry of the original space. WMD is suitable for analyzing any signal defined in a non-Euclidean space (e.g., brain mesh or other 3-D shape mesh). In the following sections, we demonstrate how WMD enhances sensitivity and statistical power of group analysis using general statistical parametric mapping processes. Since WMD is a multi-scale representation, we use Hotelling’s T² test, the multivariate version of t-test, to derive the resultant p-values.

A motivating example

Before proceeding to our experimental setup, we first demonstrate a simple analysis using WMD on a synthetically created star shaped graph. We define a function on the vertices in each graph such that this function differs by group.

Then, hypothesis tests are carried out at the vertex level. After a multiple comparison correction process such as false discovery rate (FDR), the resulting p-values are shown on a template star graph. Using such a procedure, we see that hypothesis testing using WMD seems to be more sensitive to the intrinsic group difference compared to group analysis over the original function.

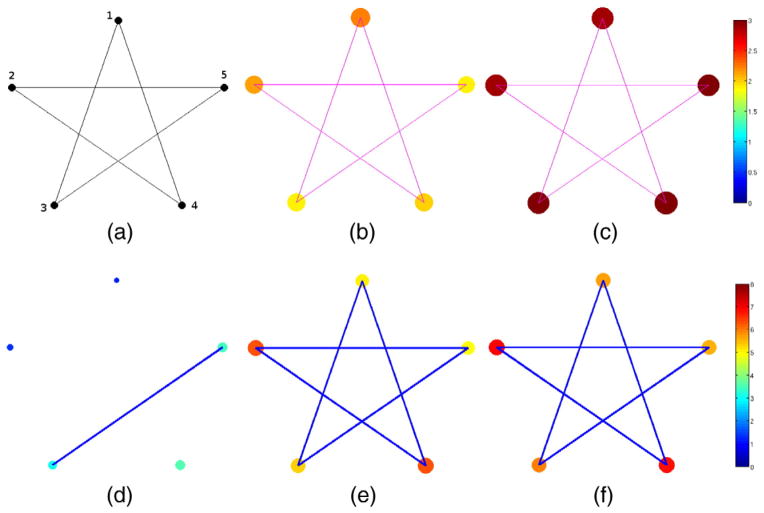
As shown in Fig. 3(a), the star graph 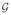consists of 5 vertices and 5 edges. We have two groups of star graphs, G⁰ and G¹, with 20 graphs in each. The index i = {1,···,40} refers to specific graphs in this set. A function f(n) is defined on the vertices of each graph: randomly drawn from two different distributions, f ( 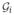∈ G⁰)~N(1, 0.1) and f( 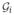∈G¹)~N(2, 0.1). Applying standard hypothesis test easily reveals the group differences in all vertices. When there are very small variations as well as a large signal (i.e., difference in group means), we obtain extremely low p-values — numerically indistinguishable from 0 — after multiple comparison correction, as expected.

Fig. 3.

Group analysis on a population of star-shaped graphs and functions defined on the vertices. a) The star graph (domain), b) Mean of noisy data from group 0, c) Mean of noisy data from group 1, d) p-value from hypothesis tests on the raw noisy data, e) p-value from hypothesis tests using MHS, f) p-value from hypothesis test using WMD. While group analysis using general routine fails, using WMD detects all vertices correctly, and the result is comparable with MHS. In d)–f), the p-values are visualized both in color and vertex sizes (larger vertex size means a lower p-value) in log10 scale.

Next, we introduce i.i.d. noise in the signal at each vertex n, and each observation h_i(n) is modeled as the sum of the true function f_i(n) and noise ε_i,n ~ N(0,1),

$$h_i(n)=f_i(n)+{\epsilon }_{i,n}.$$ (14)

In this case, the test fails to detect the true signal variations especially for this sample size. Fig. 3(d) shows an example of this failure, detecting only 2 vertices out of 5 as significant. But applying multi-scale analysis using Hotelling’s T² test on WMD shown in Fig. 3(f) finds all 5 vertices as showing significant group difference with much lower p-values. As a baseline for this experiment, we considered the heat-kernel smoothing model proposed in (Chung et al., 2005). Here, we can run the smoothing procedure at different bandwidths, collect the set of smoothed signals at these bandwidths and derive a descriptor. We call this method, multi-scale heat-kernel smoothing (MHS), which has design similarities to WMD but has distinct properties (WMD construction is based on a ‘band-pass’ type filtering behavior, while heat-kernel smoothing is inherently low-pass filtering). MHS in Fig. 3(e) used the same scale parameters as in WMD, and the performance of WMD shows a significant improvement in p-values attributable to the foregoing reasons. In Figs. 3(d)–(e), both the color and the vertex size represent the significance level — colored larger vertex sizes mean lower p-value, and those p-values are given in Table 1.

Table 1.

p-values on each vertex from the group analysis of star graphs using signal with noise, multiscale heat-kernel smoothing (MHS) and wavelet multiscale descriptor (WMD).

Vertex	1	2	3	4	5
Signal + noise	7.3e−2	4.5e−2	0.08e−2	0.03e−2	0.04e−2
MHS	8.3e−6	0.5e−6	4.38e−6	0.54e−6	11.86e−6
WMD	1.99e−6	0.105e−6	1.159e−6	0.134e−6	2.82e−6

Experimental setup

In this section, we describe datasets and implementation details for the experiment. We make use of two different datasets, the publicly available Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset and data acquired at Wisconsin Alzheimer’s Disease Research Center (ADRC). In both cohorts, the structural T1-weighted MRI data from the patients were processed by Freesurfer (Fischl, 2012), the standard tool to obtain cortical surface data and overlay functional MRI data on to the acquired brain surface. Once the MRI data is processed, it provides the brain surface model as a 3-D triangular mesh and the cortical thickness values are defined on each vertex.

ADNI data

From the ADNI dataset,³ we selected 356 subjects from two different group populations, 160 AD and the 196 healthy controls. Demographic details of the subjects are given in Table 2. These two groups lie at the opposite ends of the AD spectrum and the number of subjects is sufficient for group analysis. Therefore, we expect the standard method (apply hypothesis tests to the cortical thickness signal directly) to perform well and yield significant group differences. It will nonetheless provide a baseline to assess whether the multi-resolution representation yields any improvements at all.

Table 2.

Demographic details and baseline cognitive status measure of the ADNI dataset.

ADNI data
Category	AD (mean)	AD (s.d.)	Ctrl (mean)	Ctrl (s.d.)
# of subjects	160	–	196	–
Age	75.53	7.41	76.09	5.13
Gender (M/F)	86/74	–	101/95	–
Years of education	13.81	4.61	15.87	3.23
CDR (SB)	4.32	1.59	0.03	0.13
MMSE at baseline	21.83	5.98	28.87	3.09

CDR: clinical dementia rating, SB: sum of boxes, MMSE: mini mental state examination.

Wisconsin ADRC data

The Wisconsin ADRC dataset consists of a total of 269 subjects at this point (and increasing), categorized by AD, controls, and mild cognitive impairment (MCI). We used available data from 134 participants including 42 AD, 42 MCI and 50 older controls (see Table 3). These individuals were diagnostically characterized in the WADRC’s multidisciplinary consensus conferences using applicable clinical criteria (McKhann et al., 1984; Petersen et al., 2001). All MCI cases were of the single or multi-domain amnestic subtype whose etiology was attributed to AD. The University of Wisconsin Institutional Review Board approved all study procedures and each participant provided signed informed consent before participation.

Table 3.

Demographic details and baseline cognitive status measure of the Wisconsin ADRC dataset.

ADRC data
Category	AD (mean)	AD (s.d.)	MCI (mean)	MCI (s.d.)	Ctrl (mean)	Ctrl (s.d.)
# of subjects	42	–	42	–	50	–
Age	76.69	10.01	75.62	7.9	76.32	5.5
Gender (M/F)	22/20	–	33/9	–	19/31	–
Years of education	14.41	2.8	16.77	2.74	15.84	2.85
CDR (SB)	4.9	1.99	1.9	0.48	0.14	0.4
MMSE at baseline	21.25	4.27	26.9	1.96	29	0.99

CDR: clinical dementia rating, SB: sum of boxes, MMSE: mini mental state examination.

To acquire the data, the MRI scans were obtained in the axial plane on a GE x750 3.0-T scanner with an 8-channel phased array head coil (General Electric, Waukesha, WI). 3-D T1-weighted inversion recovery-prepared spoil gradient echo scans were collected using the following parameters: inversion time (TI)/echo time (TE)/repetition time (TR) = 450ms/3.2ms/8.2ms, flip angle = 12°, slice thickness = 1 mm (no gap), field of view (FOV) = 256 mm, matrix size =256mm × 256mm times 156mm, and in-plane resolution = 1mm × 1mm.

Implementation settings

Our framework is implemented using the spectral graph wavelet transform (SGWT) toolbox from Hammond et al. (2011) as a submodule. First, the graph representation 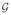of a surface mesh is derived from its Delaunay triangulation, which gives a vertex set as well as a set of faces, each of which is comprised of a 3-tuple of vertices. From these we can extract a binary edge relation . The cortical thickness values are then computed on each vertex by Freesurfer (Fischl, 2012), which is a function f(n) (or a signal) defined at each vertex n .

In order to reduce noise in a way which will preserve the type of signal captured by WMD, we apply heat-kernel smoothing (Chung et al., 2005; Zhang and Hancock, 2008) at t = 0.5 to the raw cortical thickness values prior to computing WMD. Recall that this type of smoothing requires a forward wavelet transform, followed by a scaling of coefficients according to the heat kernel function, and finally an inverse transform to reconstruct the smoothed thickness function. We approximate the inverse SGWT using a conjugate gradient method, stopping when an error tolerance of 10⁻⁶ is achieved. The degree was set to 10 for the Chebyshev approximation of the wavelet transformation in SGWT.

In our experiments, we used the default spline wavelet design provided by SGWT toolbox as the kernel function g, which is a piecewise function,

$$g(x;\alpha ,\beta ,x_1,x_2)=\{\begin{array}{cc}{x}_1^{-\alpha }{x}_2^{\alpha }& \text{for}{\mathit{xbx}}_1\\ s(x)& \text{for}{x}_1\le x\le x_2\\ x_2^{\beta }{x}_2^{-\beta }& \text{for}{\mathit{xNx}}_2\end{array}$$ (15)

where s(x) = −5 + 11x − 6x² + x³, α = β = 1, x₁ = 1 and x₂ = 2. Scales of g are defined as equally spaced bands in log scale in the spectrum of graph Laplacian. Here, the choice of the number of scales is important and must be made empirically (details below). We also note that since it is not feasible to eigendecompose a graph Laplacian when there are more than 10⁵ vertices within a brain surface, we cannot easily access the full spectrum. What we can do instead is to find the largest eigenvalue, and then divide the spectrum into a number of bins, giving the different scales. Hence, the method has just one tunable parameter, which is the number of bins (i.e., the number of scales). This has to be a small integer, meaning that there are a very small number of values that this parameter can take, if one sets this parameter using a validation test empirically. Because noise generally lies at high end of the spectrum, we only used the scales of lower end of the spectrum to define the WMD. Those scales of interests are chosen by incrementally adding band of the scales from the coarser scale until results are satisfactory, and the remaining scales are discarded.

Since we have multiple brain surfaces, the range of the entire spectrum is defined by the largest eigenvalue of the graph Laplacians of all subjects. Defining wavelets in the common spectrum ensures that we define the same wavelet transform over the group of subjects. The range of the eigenvalue spectrum was [0,25.7] for the ADNI dataset and [0,30.13] for the ADRC dataset. To divide up the spectrum, we ran experiments by setting the total number of scales to 5, 6 and 7. We observed empirically that 5 and 7 scales respectively for ADNI and ADRC dataset were more effective. Next, one must choose how many scales will be used to define the actual descriptor for statistical analysis. We found that using the first four scales for both datasets yields reliably noting that other choices for these parameters yield comparable results.

Experimental framework and statistical analysis

The goal of our experiments was to assess the improvement in the ability to detect group differences using WMD versus using cortical thickness on its own. The results of these experiments will be described in the next section. As a proof of principle, we first performed group analysis on synthetically constructed brain surface data to show that WMD enhances the sensitivity of statistical analysis. Next, we present experiments on the ADNI and ADRC datasets.

We follow the general analysis pipeline in SPM by plotting the corresponding p-values on the template brain surface after FDR correction. We additionally apply heat-kernel smoothing on the cortical thickness to compare the group analysis result. To compute the p-values, we use a t-test on univariate variables (i.e., raw and smoothed cortical thickness) and Hotelling’s T² test and Multivariate General Linear Model (MGLM) with Hotelling–Lawley trace on the multivariate variables of interest (i.e., WMD). Using MGLM, we control for the effects driven by factors that are not directly related to the disease (i.e., age or gender) to obtain a more accurate result.

Since our fundamental argument is that multivariate WMD is more sensitive than performing statistical tests on univariate cortical thickness, one should expect to see a stronger signal than results derived via smoothed or raw cortical thickness. Similarly, since the ADNI has a far larger sample size than the ADRC, we hope to see stronger signal in the ADNI results, but similar cortical regions should show up in the ADRC analysis as well.

Experimental results

In this section, we give a detailed description of the experiments performed on synthetic data as well as the two Alzheimer’s disease datasets described in the previous section.

Simulation of surface-based group analysis and ROC response

We first demonstrate group analysis using WMD on a synthetically generated cortical thickness (and atrophy) on a template brain surface. The template brain surface consists of 2790 vertices and 5576 faces, and 20 diseased and 20 control subjects are artificially created using the template brain. First, a synthetic baseline global cortical thickness signal of mean 2 mm and variance 0.1 is introduced. This is shown as the blue region in Fig. 4. Note that this region is viewed as not affected by disease and so no group differences should be identifiable in these regions. Next, we define two diseased regions (green and red) in Fig. 4. These regions undergo varying levels of atrophy (relative to the ‘default’ cortical thickness signal in blue). The green region corresponds to a mean atrophy of 0.2 mm (variance 0.02 mm) and the red region corresponds to a mean atrophy of 0.4 mm (variance 0.04 mm) affected on the default (blue) cortical thickness signal. The red and green regions cumulatively correspond to a total of 889 vertices (32% of the brain region). Finally, we add noise from N(0,1) to the cortical thickness signal obtained from the above procedure.

Fig. 4.

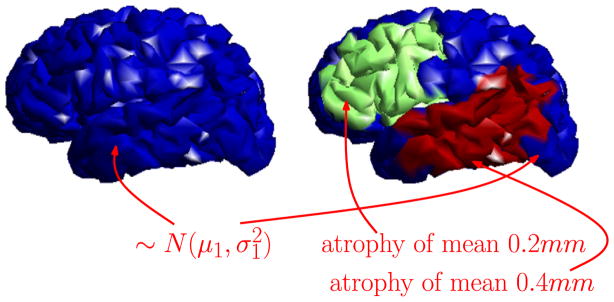
Simulation setup of synthetic cortical thickness and atrophies on brain surfaces. Blue regions correspond to the default (non-diseased) cortical thickness signal, μ₁ = 2mm, ${\sigma }_1^2=0.01$. Green and red correspond to disease regions which undergo atrophy affected on the default cortical thickness signal. These atrophy levels are about ~ 25% and ~ 50% of the actual atrophies measured in AD specific regions of a real dataset.

From the above data, we obtain smoothed CT and WMD for comparison. Smoothing is performed via heat-kernel smoothing with bandwidth of 0.5. The spectrum of graph Laplacian is [0,18.5], and this range is divided into 6 bins including the scaling function in order to define WMD. The spline kernel function g from SGWT toolbox is used to obtain the WMD.

For statistical group analysis, a t-test was used for univariate raw data and smoothed data, and we used Hotelling’s T² test for multivariate analysis for WMD. The resultant p-values are shown on the template surface in − log10 scale for comparison, see Fig. 5.

Fig. 5.

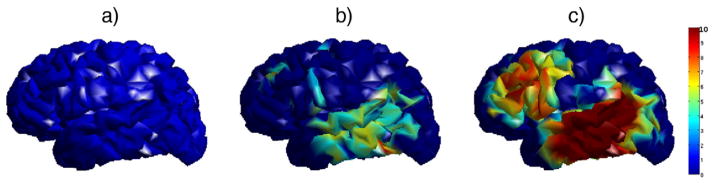
Simulation of surface based group analysis. The resultant p-values in − log10 scale after FDR at q = 0.01 are mapped on the template brain surface. a) Result using raw CT, b) result using heat-kernel smoothing (t = 0.5), c) result using WMD (4 scales out of 6).

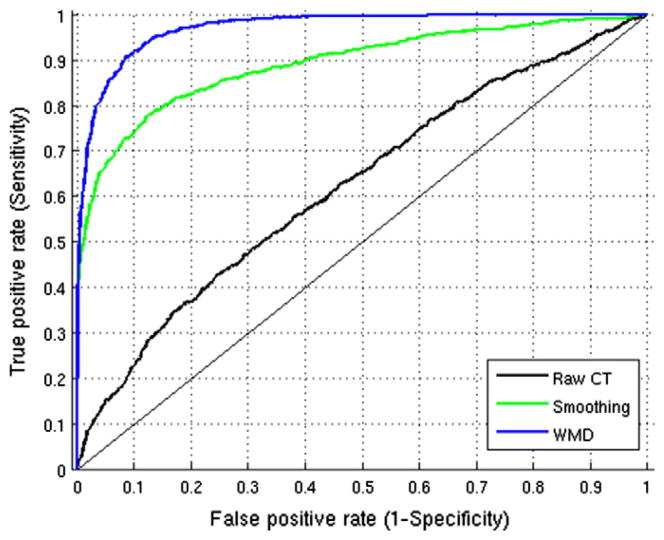
It is well known that filtering raw data improves sensitivity, however, over-filtering of data may end up detecting many false positives. Multiple comparison correction is generally applied to control the type I error in most studies. In this simulation, however, we know the ground truth from the synthetic atrophy model — a label for each vertex indicates whether it atrophies or not; so, we can conduct an ROC analysis to observe the sensitivity and specificity relationship. Here, the aim is to show that we are not only increasing the sensitivity, but we also do not make specificity worse using WMD. From this group analysis, we obtain p-values at each vertex, which tells us whether to reject the null hypothesis: the two distributions from the data at each vertex are the same. When the null hypothesis is rejected, we find those vertices with significant differences, and we can use (1 − p) as a measure to determine the label for each vertex. The resultant ROC curve is given in Fig. 6, and we measure the area under the curve (AUC). We see that the raw data gives an AUC measure of 0.623, when heat-kernel smoothing is used the AUC is increased to 0.892. But using WMD yields the best AUC of 0.971 suggesting that increased sensitivity does not come at the cost of poor specificity.

Fig. 6.

ROC curve using p-values from statistical group analysis on Raw CT, Smoothing and WMD with AUC of 0:623, 0:892 and 0:971 respectively.

Remark

Based on the simulation results, we may ask why a classical group analysis on the raw cortical thickness signal is not detecting stronger signal differences, especially since the atrophy has a relatively large affectation. There are two reasons for this behavior relating to the level of atrophy introduced in these simulations (which are not very large) and the small sample sizes. Recall that the synthetic atrophy was set to ~ 50 % and ~ 25 % of the mean difference in atrophy levels in disease specific regions measured in a real dataset (which was about 0.82mm). Also, the sample sizes are relatively small (20 healthy controls and 20 diseased). We will see shortly that when the atrophy differences and the sample sizes are larger, classical analysis on cortical thickness can indeed detect regions exhibiting group-level differences.

ADNI dataset

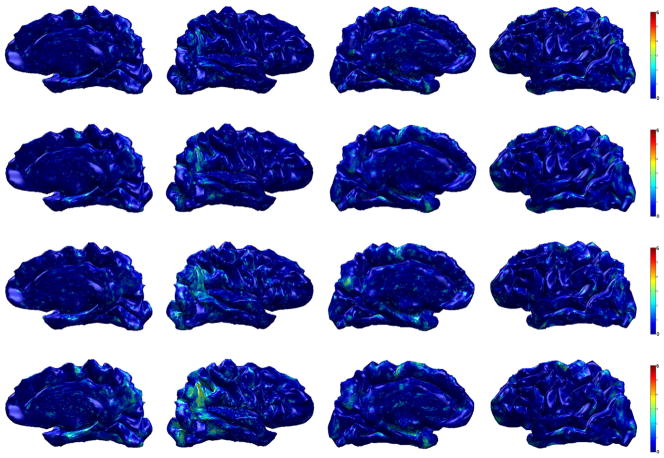
We performed four different analyses using different types of descriptors and statistical methods. We used heat-kernel smoothing (Chung et al., 2005) to smooth the data, and compare the group analysis result with the result using WMD. We applied t-test on the raw thickness and smoothed thickness, when the given data are univariate, and Hotelling’s T² and MGLM on WMD, which consists of multiple variables at each vertex. Using MGLM, we remove the effect of age and gender, which are known to affect the cortical thickness measurements regardless of the disorder. Fig. 7 shows the resulting p-values in increasing order from all four analysis on the left hemisphere of the brain and the FDR threshold at q = 1e⁻⁵. We performed group analysis using 60%, 80%, and 100% of the total sample size (i.e., emulating the setting that the study size was smaller), and observe that the curve from the sorted p-value is shifted with increase in the sample sizes. As a result, the number of vertices that survive the FDR threshold increases with larger dataset, and a much larger number of vertices survive using WMD than those analysis using raw and smoothed cortical thickness. We further plot these p-values on a template brain surface to see which regions of brain are affected, and whether these are meaningful for AD.

Fig. 7.

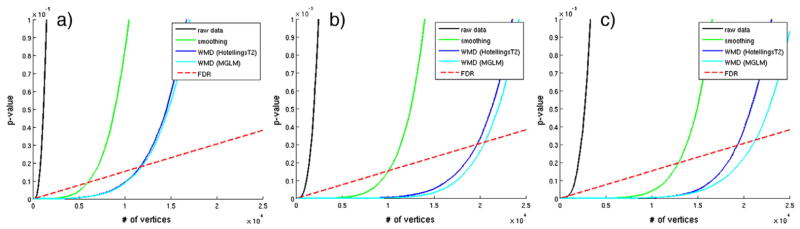
Plot of sorted p-values and FDR threshold from AD vs. Controls analysis according to different sample sizes using ADNI dataset. a) Using 60% of the total subjects, b) using 80% of the total subjects, c) using all subjects. As the sample size increases, the number of surviving vertices increases. We can see that WMD is much more sensitive than smoothing.

Group analysis

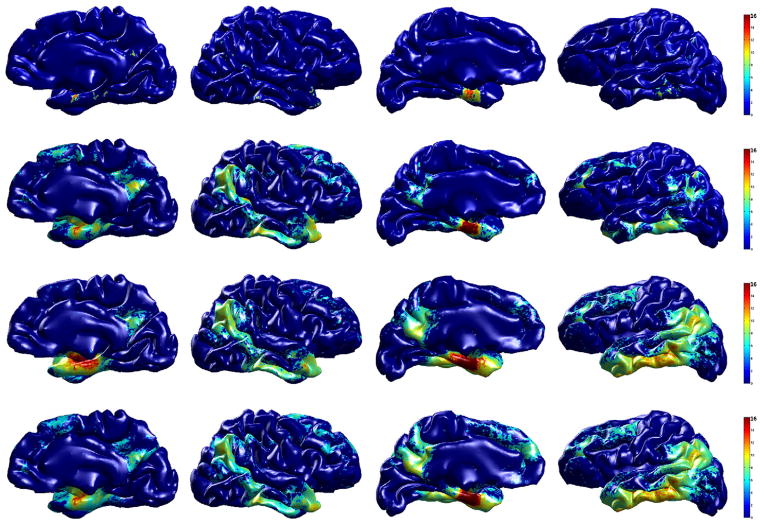
The top row of Fig. 8 shows the standard hypothesis testing result on the raw cortical thickness data, and we are able to find only small regions using this analysis. Using smoothed cortical thickness, although it correctly finds the underlying signal (shown in the second row of Fig. 8), the result using WMD (shown in the third and fourth rows of Fig. 8) detects even larger regions of the brain with much improved statistical result (notice the red regions). From these comparisons, it seems that WMD makes the underlying true signal more sensitive and thereby improves results of the statistical analysis. Among 13,1076 vertices on both left and right hemispheres, we find only 1228 vertices (0.9%) using the raw cortical thickness data. After applying kernel smoothing method, the number of identified vertices as showing group differences goes up to 22,464 (17.1%).

Fig. 8.

Group analysis result (AD vs. controls) on ADNI dataset. The resulting p-values (in − log₁₀ scale) from hypothesis tests after FDR at q = 1e⁻⁵ are shown on a template brain surface. First row: t-test on the raw cortical thickness, second row: t-test on smoothed data (SPHARM), third row: Hotelling’s T² test on WMD, fourth row: MGLM on WMD (age and gender effect removed). We can see that smoothing the cortical thickness works better than the raw data, but WMD improves the statistical result much more.

Using Hotelling’s T² test on WMD gives 31,078 (23.7%) vertices and after removing age and gender effect, MGLM detected 34,472 (26.3%) vertices. All four analyses using raw cortical thickness, smoothed cortical thickness, and WMD (Hotelling’s T² test and MGLM) revealed strong signal on the anterior entorhinal cortex in the mesial temporal lobe, however, we can observe that WMD is much more sensitive relative to the univariate analysis not only in this particular location, but also in the posterior cingulate, precuneus, lateral parietal lobe and dorsolateral frontal lobe. The identified regions are already well-known to be implicated in AD (Lehmann et al., 2011; Lerch et al., 2005; Thompson et al., 2004).

ADRC dataset

On the ADRC data, we compared AD vs. controls, AD vs. MCI, and MCI vs. controls. In the AD vs. controls analysis, we expect to detect similar brain regions found in the result using the ADNI. In the AD vs. MCI and MCI vs. controls analyses, we simply show which brain regions are showing morphological changes between groups.

AD vs. controls

Group analysis

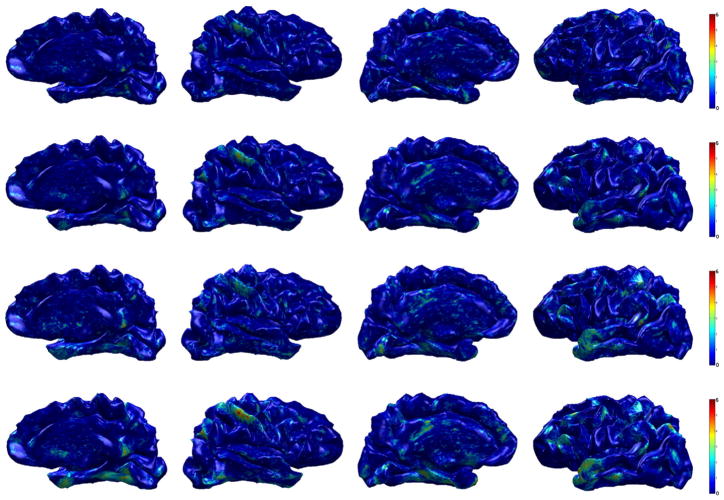
We first analyze a group differences on AD and control subjects. Compared to the ADNI dataset, here we have smaller number of subjects. Applying general hypothesis testing directly fails to detect any group differences using the raw cortical thickness due to the small sample size. Fig. 9 shows the resulting p-values in increasing order from student’s t-test using cortical thickness and smoothed cortical thickness (heat-kernel smoothing at t = 0.5), and Hotelling’s T² test and MGLM using WMD. FDR threshold at q = 0.1 is plotted in red dotted line, and the number of vertices that are below the threshold level is considered as the signal showing significant group differences. We see that while it is difficult to find a meaningful signal using raw cortical thickness estimates on the ADRC dataset, WMD easily detects the underlying difference. On 131,076 vertices on both the right and left hemispheres of the brain surface (65,538 tests on each hemisphere), we apply t-test on the cortical thickness data and heat-kernel smoothed data, Hotelling’s T² test on WMD, and MGLM on WMD. After FDR at q = 0.05, we detect each 622, 5913, 12,455, 13,769 vertices from the t-test, Hotelling’s T² test, and MGLM respectively, which corresponds to 0.47%, 4.51%, 9.5%, and 10.5% of the total number of tests performed.

Fig. 9.

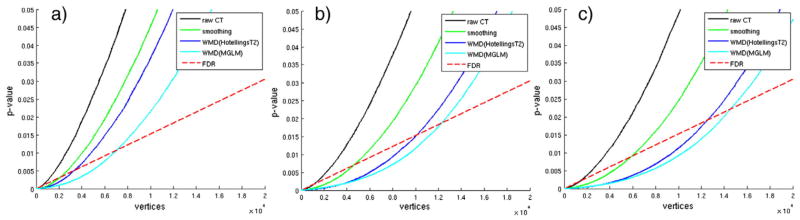
Plot of sorted p-values and FDR threshold at q = 0.1 from AD vs. controls analysis on the right hemisphere of the brain according to different sample sizes using ADRC dataset. a) Using 60% of the total subjects, b) using 80% of the total subjects, c) using all subjects. As the sample size increases, the number of surviving vertices increases. We can see that WMD increases the sensitivity.

In Fig. 10, we compare the four different results using different features and statistical techniques on the template brain surface. In the top two rows, the result using raw cortical thickness and smoothed cortical thickness is presented. The smoothed cortical thickness helps the test detect some signal variation, but the result is weak and almost does not reveal any brain region. However, WMD increases sensitivity, detecting many more regions with lower p-values (using Hotelling’s T² test); the result is shown in the third row of Fig. 10. Since variation of cortical thickness may be caused by age or gender, we further utilize MGLM to remove the age and gender effects. As seen in the bottom row of Fig. 10, the signal becomes more concentrated at specific regions.

Fig. 10.

Group analysis result (AD vs. controls) on ADRC dataset. The resulting p-value (in − log₁₀ scale) from hypothesis tests after FDR at q = 0.05 is shown on a template brain surface. First row: t-test on the raw cortical thickness data, Second row: t-test on the smoothed data, third row: Hotelling’s T² test on WMD, fourth row: MGLM on WMD (without age and gender effect).

Using cortical thickness and smoothing, we observe differences in a very small region in the right inferolateral lobe only. However, using WMD, we find very strong group differences in the bilateral inferolateral parietal as well as temporal pole and parahippocampal cortex. Other than those regions, we also find isthmus cingulate, posterior cingulate, superior frontal, precuneus, and entorhinal cortex on both the right and left hemispheres as showing group differences. Since we found similar regions using ADNI dataset, it is reasonable to conclude that our results on ADNI and ADRC are in agreement.

AD vs. MCI and MCI vs. controls

Group analysis

We also compare AD vs. MCI and MCI vs. controls group, and the results are shown in Figs. 11 and 12. In these analysis, we show the uncorrected p-values using Hotelling’s T² test and MGLM (removing age and gender effect) on WMD. The first row in Figs. 11 and 12 represents the result using cortical thickness, the second row is the result using heat-kernel smoothing (t = 0.5), and the third and fourth rows show the result using WMD by applying Hotelling’s T² test and MGLM respectively. These comparisons provide additional evidence that analysis with WMD is more sensitive, and more quantitative results are shown in the Goodness of Fit Results on the ADRC dataset section.

Fig. 11.

Group differences (AD vs. MCI) on ADRC dataset. First row: p-values (uncorrected) from t-test using CT, second row: p-values (uncorrected) from t-test on smoothed data, third row: p-values (uncorrected) from Hotelling’s T² test on WMD, fourth row: p-values (uncorrected) from MGLM on WMD (age and gender effect removed.).

Fig. 12.

Group differences (MCI vs. controls) on ADRC dataset. First row: p-values (uncorrected) from t-test using CT, second row: p-values (uncorrected) from t-test on smoothed data, third row: p-values (uncorrected) from Hotelling’s T² test on WMD, fourth row: p-values (uncorrected) from MGLM on WMD (age and gender effect removed).

In both AD vs. MCI and MCI vs. controls analyses, we expect to see similar brain regions identified by the AD vs. controls analysis, with small differences. By comparing MCI with AD and controls, we may assess the longitudinal progression of the disease in specific brain regions. On AD vs. MCI, the results showed differences in precuneus, inferior frontal and lateral occipital on both hemispheres. Relatively weaker differences in the temporal pole and parahippocampal regions are seen. As identified from the AD vs. controls analysis, the changes in cortical thickness occur in the precuneus, inferior frontal, temporal pole and parahippocampal regions as a subject enters MCI. In the MCI vs. CN analysis, we observed changes in the precuneus, isthmus cingulate, inferior parietal, inferior temporal, superior temporal and temporal pole. Although not reported in previous works, the MCI and CN comparison showed potential changes in the postcentral region as well.

Power analysis

Next, we assess the improvement in group analysis in terms of statistical power and calculate the number of subject required to identify the differences. We first select the vertices that show p < 0.05 from the ADNI dataset, and these vertices are used to evaluate the statistical power in the ADRC dataset. We use the mean and variance from the selected vertices from each subject in ADRC dataset to perform power analysis. Following Hinrichs et al. (2012), the sample size per group n at a certain confidence level α and power level 1 − β is computed as

$$n=\frac{2{\sigma }^2{\left(Z_{1-\alpha /2}+Z_{1-\beta }\right)}^2}{{\delta }^2}$$ (16)

where Z_{1 − α} is the upper α/2 percentile from the standard Normal distribution, σ² is the variance of the descriptor, 1 − β is the desired power and δ is the effect size. As a result, we obtain the number of samples needed in order to get a significant result to observe the induced variations (i.e., at power 80%) using cortical thickness and WMD.

The summarized result is shown in Table 4. The power analysis was carried out on the cortical thickness and 4 scales of WMD used in other experiments, both concatenated and individually. Since WMD results from a filtering operation from the wavelet transformation, suppressing high frequency components has the effect of reducing noise and variation. Consequently, WMD decreases the required sample size in most cases as shown in Table 4.

Table 4.

Estimated sample sizes to observe the differences between AD and controls using cortical thickness and WMD at α = 0.05 and 1 − β = 0.8. The scales in WMD were analyzed both separately and in average.

	Power	CT (univariate)	WMD (concatenated)	WMD (scale 1)	WMD (scale 2)	WMD (scale 3)	WMD (scale 4)
Right hemisphere	0.8	22	18	18	19	21	24
	0.9	29	24	24	25	28	33
Left hemisphere	0.8	20	16	17	18	16	18
	0.9	27	22	22	24	22	23

Goodness of fit results on the ADRC dataset

In order to quantitatively assess the improvement in sensitivity, we compare the R² using raw cortical thickness and WMD from a linear model which is,

$$Y=BX$$ (17)

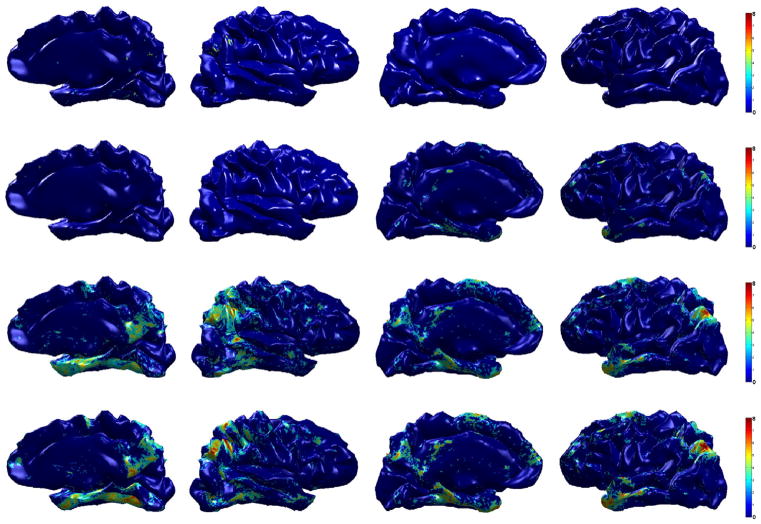
where Y is the response variable (i.e., cortical thickness or WMD), and X is the model (i.e., group). For the multivariate response variable WMD, we used Wilk’s Lambda to compute the R². The R² indicates how well the data fit the given model, and the result shown in Fig. 13 tells us that our WMD fits the model or explains more variance in the model much better than cortical thickness in the AD vs. controls analysis. This shows the improvement in sensitivity using WMD even to subtle effects. Further analysis on AD vs. MCI and MCI vs. controls is shown in Figs. 14 and 15. These results also indicate that WMD is more sensitive, and can reveal group differences which may be too weak to detect with the classical analysis.

Fig. 13.

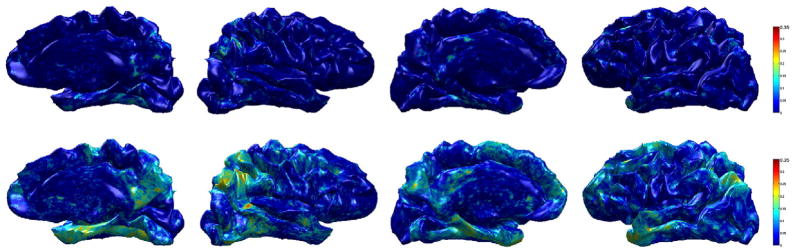
Sensitivity brain map using R² (AD vs. CN) on ADRC dataset. Top row: R² using raw cortical thickness, Bottom row: R² using WMD. We can see that the model fits WMD better than cortical thickness, therefore WMD is more sensitive to the group difference than the raw cortical thickness.

Fig. 14.

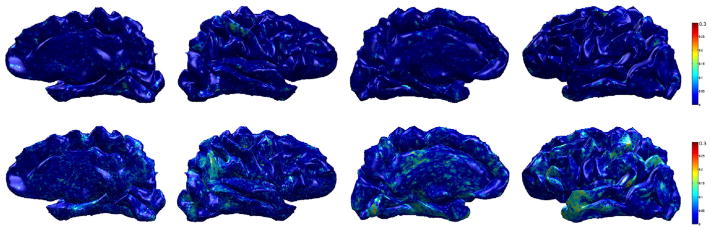
Sensitivity brain map using R² (AD vs. MCI) on ADRC dataset. Top row: R² using raw cortical thickness, bottom row: R² using WMD. We can see that the model fits WMD better than cortical thickness, therefore WMD is more sensitive to the group difference than the raw cortical thickness.

Fig. 15.

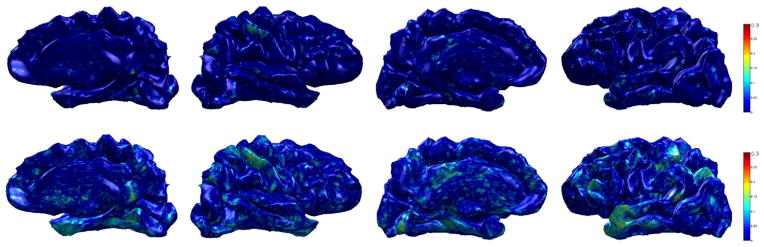
Sensitivity brain map using R² (MCI vs. controls) on ADRC dataset. Top row: R² using raw cortical thickness, bottom row: R² using WMD. We can see that the model fits WMD better than cortical thickness, therefore WMD is more sensitive to the group difference than the raw cortical thickness.

Discussion

Surface based mapping analysis is a widely deployed procedure in neuroimaging where we use mass univariate tests, (e.g., t-test or GLM type analysis) along with multiple comparisons correction to detect and assess statistically significant differences between clinical, genotype, or other groups of interest. The aim then is to derive maps showing the degree of significance of group level effects so as to localize regions of interest. This approach works very well when there are a sufficient number of subjects in the study, and when the analysis method is sensitive enough to identify such group differences. However, these assumptions may not always hold, which necessitates the design of mechanisms that are sensitive enough to identify variations even in the smaller sample size regime. In this work, we have focused on improving the sensitivity of the extracted features, so as to mitigate the dependence on sample size.

To this end, we derived wavelet based multi-scale descriptors (WMDs) of the cortical thickness signals which are sensitive both to surface geometry/topology, as well as variations at different spatial scales. As noted above, a graph (typically) defines a non-Euclidean space, and the appropriate tools completely capture its geometry and topology. Therefore, wavelet theory lends itself nicely to the problem of deriving useful scale-dependent features. This construction is based on a set of elegant results in the harmonic analysis literature dealing with the spectral graph wavelet transform (Hammond et al., 2011) and diffusion wavelets (Coifman and Maggioni, 2006). This allows us to propose a multivariate approach for group analysis of surface based signals in neuroimaging settings.

Instead of mapping the data onto a sphere, as in traditional spherical harmonic (SPHARM) based methods, our multi-scale shape descriptor is directly defined on the cortical surface graph itself, completely bypassing the ballooning process. Further, the WMD method is sensitive to signals at different scales unlike SPHARM based methods. In our WMD construction, each scale represents a different level of support over the harmonic basis. By varying a window over the harmonic spectrum, the method of WMD efficiently characterizes both local and global contexts around each vertex. As the window moves toward to the lower frequency spectrum, the wavelet frame becomes more overcomplete. To avoid this, subsampling is done in grid based Euclidean spaces. However, when dealing with non-Euclidean spaces, without making any assumption on the nature of the graph, there is not necessarily a clear concept of subsampling. We note, for instance, that the method described in Narang and Ortega (2012) gives a method of subsampling, but only in bipartite graphs, and other methods can do this by making other assumptions. For instance, the method in Coifman and Maggioni (2006) assumes that the spectrum decays. Because there is no subsapling scheme on graphs, spatial correlations are induced between nearby vertices in the lower frequency range. The authors in Van De Ville et al. (2004) propose to deal with the spatial correlation issue by leveraging the compact, localized support of wavelets. In various situations, the above decimated strategy is preferable, however, the subsampling needed in such a scheme makes interpreting the specific band-pass filtering behavior difficult. Instead, the non-decimated scheme adopted here is more convenient for analysis purposes because avoiding subsampling enables deriving a descriptor precisely at the given set of vertices.

Through our experiments we demonstrated that such a multi-resolutional shape descriptor defined in a graph space can be a powerful and flexible tool for identifying group difference signals. Indeed, a method with greater sensitivity to group differences would require recruitment of fewer subjects. We primarily evaluated the WMD framework on cortical surface signals, comparing group analysis results with WMDs against classical methods. We first compared these models using ROC curves for group analysis on synthetic brain surface data. Relative to raw uni-scale measurements, or with smoothing, we identified brain regions with much stronger group differences with global FDR correction, and in some cases these were detected when classical methods fail. In the ADNI dataset, we obtained pronounced group differences in the anterior entorhinal cortex, posterior cingulate, precuneus, lateral parietal lobe and dorsolateral frontal lobe. Similar regions were found using the distinct W-ADRC dataset as well. It is encouraging that these independent results are in agreement; we also note that these regions are consistent with the literature (Lehmann et al., 2011; Thompson et al., 2011; Wirth et al., 2013). In addition to these results, we applied MGLM analysis to control for factors such as age and gender and show how these factors change the results. The FDR-curves suggest that up to twenty-eight times more vertices using WMD than using raw cortical thickness can survive global correction. Using the W-ADRC dataset, we further analyzed the effect from MCI. We showed that WMDs obtain lower p-values than raw cortical thickness, and displayed whole-brain sensitivity map using the R² metric of effect size. Finally, the power analysis on AD and controls using cortical thickness and WMD indicates that WMD is more sensitive, giving smaller sample size estimates. By applying our framework on two different datasets: the ADNI dataset (a large and well characterized dataset) and the W-ADRC dataset (central to a number of local studies), we have demonstrated that the methodology is broadly applicable.

We believe, for several reasons, that the improved sensitivity is attributable to the filtering effect achieved by separating high-frequency information from low-frequencies. First, anatomical brain features and neurodegenerative morbidity effects tend to exhibit a certain degree of spatial cohesion and locality (Braak and Braak, 1995; Hinrichs et al., 2009). In addition, most noise processes, whether derived from scanner effects or post-processing, tend to be distributed across all scales. Gaussian smoothing and filtering are therefore quite common for this and other reasons. Note however, that a non-adaptive Gaussian blur kernel is oblivious to anatomical divisions such as sulci and cortical boundaries, and may inappropriately mix signals which are close spatially, but not anatomically. Heat-kernel smoothing attempts to resolve this issue by first expanding the cortices to a spherical surface (ballooning) and then smoothing, but in doing so it smoothes all scales with the same fixed-bandwidth kernel. A key feature of the WMD approach is that each scale corresponds to a particular band-pass filter in the spatial domain, which can be thought of as smoothing only certain frequencies. In graph-based methods, smoothing can, and indeed must, be done separately for each scale because there is a strong dependence on the unique topology of each subject’s cortical surface mesh. In the interest of space, we do not report the effect of using all seven scales, (as opposed to treating the upper three as “high-frequency” signal and discarding them as noise), but briefly, doing so uniformly weakened results and lessened significance. Moreover, the high frequency components simply did not correspond with any identifiable brain regions, and visually resembled a random “speckle” pattern. This is an important observation because in some image processing domains high-frequency information can give well-defined edges, but this did not appear to be the case in this application.

One concern about using the binary edge weights in the adjacency matrices (the distance between vertices is not reflected) is that results from non-uniform sampling (based on the underlying topology of the surface and/or the signal) and from a uniform or grid-like sampling will be different. In principle, this is true. However, for actual datasets, assuming that the sampling resolution is fine/high enough to capture variations in the shape topology of the brain surface and the signal distributed on it, the final results of the statistical analysis are not much different. Empirically, the default sampling in Freesurfer (Fischl, 2012) seems to be sufficient for our analysis using binary adjacency matrices. A discussion of this phenomenon with a toy example is shown in Appendix B.

Although we have demonstrated that our framework is able to obtain strong and robust results in group analysis, there are nevertheless a few shortcomings. Our method leaves it to the user to define the scales, and we note that this is often the case in wavelet-based methods. Ideally, one would like to eigen-decompose the entire graph Laplacian, and divide the spectrum into portions of roughly equal mass. However, when there are ~ 10⁵ nodes in the graph, this becomes infeasible. A more practical approach is to find the largest eigenvalue, and simply divide the spectrum into a fixed number of equal-width bins, which is the approach we followed. It still remains to choose how many such bins to use, but we found empirically that a small number, on the order of five to ten, works well. This choice is driven by several considerations. Primary among these is computational burden. Consider that WMDs contain information not only about the function defined on vertices, but also about the distinct topology of each subject’s vertex mesh. Therefore, resampling to a grid must be done subsequent to any calculation of WMDs, and it must be done independently for each scale. For a large number of scales this cost becomes a bottleneck. Moreover, we do not wish to incur the curse of dimensionality any more than is necessary. That is, while multi-resolution descriptors can effectively separate out some signals that are scale-dependent, if we allow the descriptors to unduly proliferate then we may dilute the underlying signal by spreading it too thinly over a large number of scales. Thus, while some signals genuinely exist only at a particular scale, if we choose too many scales in some neighborhood of the true signal, then this signal may “leak” between them due to sampling artifacts. Taking these issues into consideration, we avoid choosing too many scales. In our evaluations, we found that seven scales give satisfactory results, though we did not perform an exhaustive grid search because of the above mentioned constraints. In addition to the choice of number of bins is the choice of which ones to discard as high-frequency noise, and which to treat as low-frequency signal. Following a similar line of reasoning as above, we simply chose the first four bins as signal and the last three as noise. This is corroborated by the fact that the distribution of p-values of the WMDs corresponding to high frequency portions of the spectrum followed a roughly uniform distribution, and visual inspection showed no recognizable spatial cohesion. This is exactly as we expect, and is in fact the intended effect — considering that the CT signal can be recovered as a deconvolution and summation of the WMDs, and that the high frequency WMDs are designed to serve as a model of “noise”, then it is not surprising that the overall CT signal is weaker.

There is an important increase of interest in wavelet based neuroimaging analysis methodologies. A number of works have expanded the basic framework as well as adapted it to various statistical issues. Van De Ville et al. (2004) approach the problem of selecting thresholds for both wavelet and spatial domains, which is important because without addressing this issue, spatial statistical maps are uninterpretable. They tackle this issue by balancing the two thresholds in the wavelet and the spatial domain, and apply statistical testing in the spatial domain instead of the wavelet domain. The authors Leonardi and Van De Ville (2013) explored the ramifications of using tight (or Parseval) wavelet frame which more closely resembles an orthonormal basis while retaining basic wavelet properties. One of the advantages of using a tight frame is that the inverse transform is easy to compute; this plays an important role in pre-processing the raw data. In addition, it is efficient because it preserves the energy in the transformed domain. Although the tight frame formulation prevents spectral leakage between scales and proposes a much cleaner strategy than re-normalizing the coefficients, the t and T² statistics we used in the analysis automatically re-scale the coefficients regarding the difference in ranges between scales. The authors in (Leonardi and Van De Ville, (2013)) above also noted that the construction in Hammond et al. (2011) does not give a tight frame, however it is nonetheless feasible for our particular application (as shown in our experiments) because we are primarily interested in the forward transform which is essential to obtaining the descriptors.

Lastly, we observe that there is an issue of whether to account for subject specific variations in global cortical thickness. Adjustments for global effects in volumetric analyses are premised on the finding that individuals who overall have bigger heads also tend to have larger regional brain structures (e.g., hippocampus) than persons with smaller heads. Normalization of regional volumes by means of whole brain volume (whether via regression approaches or proportional scaling) is therefore necessary to control for this potential confound. In contrast, available evidence convergently indicates that cortical thickness is only minimally or not at all related to sex, height, or overall brain size. Therefore, adjusting for brain size/global thickness while performing vertex-wise cortical thickness analyses risks introducing error variance into the model (Dickerson et al., 2009; Palaniyappan, 2010; Salat et al., 2004; Whitwell et al., 2013).

Despite these unresolved issues, our results suggest that the method may be highly suitable to traditional group analysis in most cases, as is shown throughout the paper. The procedure can be easily adapted to analyze data with arbitrary topologies (Chung et al., 2005; Kim et al., 2012) and for studies dealing with other neurodegenerative disorders involving morphological measurement on the brain surface or on brain networks. We hope that the companion toolbox to this paper (available on NITRC and http://pages.wisc.edu/~wonhwa) will facilitate such developments.

Appendix A. Basic notations and spectral graph theory

The graph = { , , 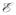ω} is a set of vertices 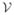, an edge set 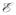, and the corresponding edge weights ω. For the graph 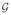with N vertices, its adjacency matrix A is defined as a N × N matrix whose elements a_ij are given as,

$$a_{ij}=\{\begin{array}{cc}{\omega }_{ij}& \text{if}i\text{th}\text{and}j\text{th}\text{vertices}\text{are}\text{connected}\\ 0& \text{otherwise}\end{array}$$ (A.1)

If is undirected, the matrix is positive symmetric, however if 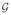is directed, A is asymmetric; the elements a_ij may represent the direction of connectivity. The degree matrix D is defined as a N × N diagonal matrix whose ith diagonal is Σ_j ω_ij, the sum of edge weights connected to the ith node. When the edge weights are binary and represent solely the connectivity information with ω_ij ∈ {0,1}, A is a binary matrix and the degree matrix D represents how many edges are connected to each vertex. From these two matrices that characterize the geometric property of a graph, the graph Laplacian L is derived as:

$$\mathbf{L}=\mathbf{D}-\mathbf{A}$$ (A.2)

and the normalized version is given as,

$${\mathbf{L}}_{\mathit{norm}}=I-{\mathbf{D}}^{-1/2}{\mathbf{AD}}^{-1/2}={\mathbf{D}}^{-1/2}{\mathbf{LD}}^{-1/2}.$$ (A.3)

Illustrative examples of A,D and L of a star shaped undirected graph with 5 vertices and 5 edges are shown in Fig. A.16.

Note that L ⪰ 0 and so has a complete set of orthonormal eigenfunctions χ_l, and the corresponding eigenvalues λ_l for l = 0,1,…, N − 1 are ordered as

$$0={\lambda }_0\le {\lambda }_1\le \dots \le {\lambda }_{N-1}.$$ (A.4)

Fig. A.16.

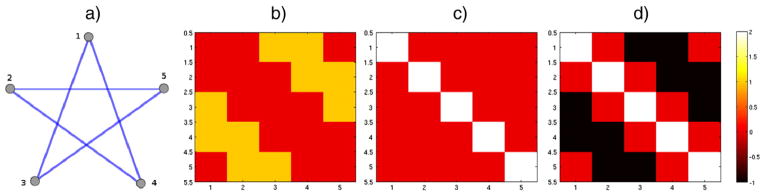
An example of A,D,L. a) A star shaped graph 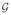with 5 vertices and 5 edges. b) adjacency matrix A, c) degree matrix D, d) graph Laplacian L.

Appendix B. Effect of non-uniform versus uniform mesh sampling

This section shows an additional experiment to address the effect of sampling schemes. Briefly, if the edge weights in the adjacency matrices are binary, non-uniform/uniform sampling of a domain (which is a brain surface in our case) may affect the group analysis result depending on the sampling resolution. If the sampling is coarse, then a binary adjacency matrix is likely to yield a poorer result because it assigns a unit edge weight to all neighboring vertices regardless of their distances. But if the sampling resolution is high enough such that neighboring vertices are sufficiently close and dense enough to characterize the brain surface, then the effect of binary edge weights becomes far less important.

This phenomenon is demonstrated in Fig. B.17. We simulate two groups of 20 images each (40 images in all). The images in the first group have a signal which we hope to identify later in group analysis. Signal measurements come from a Gaussian distribution 1 + N(0,0.01) in a circular region of radius 10 at the center of a 2D domain ([0,100] for each axis). Such a signal is not introduced in the second group of images. Finally, we add Gaussian noise from N(0,0.5) to all images. Given this data, we evaluate various sampling schemes and their effect on group analysis results using our WMD framework. We evaluate two different sampling schemes: 2000 (coarse) and 10,000 (dense) vertices from the 2D domain. For each sampling scheme, we draw samples uniformly and non-uniformly and then measure the differences at each vertex to identify regions that are statistically different. For the non-uniform sampling, we used a Gaussian distribution centered at various grid points (multiples of 20, see Fig. B.17) in the [0,100] domain in the x,y axes with variance (2,2). This means that we will sample more points which lie closer to such grid-points. With the sampled vertices, we generate Delaunay triangular meshes to create the underlying graph. These graphs (meshes) are shown in Figs. B.17a), b), e) and f). Once we defined these graphs, we applied our framework to find group differences, which is a circle of radius 10 at (50,50). The resultant p-values after Bonferroni correction at 0.01 are shown in Figs. B.17c), d), g) and h). For 2000 vertices, the group analysis result from the uniform sampling yields moderate results (in terms of visual overlap of detected differences with true differences), whereas the non-uniform sampling returns a relatively weaker result in terms of visual overlap. However, as the resolution of sampling improves to 10,000 vertices, it is sufficiently dense and both uniform and non-uniform sampling methods reliably identify the true difference between the two groups.

Fig. B.17.

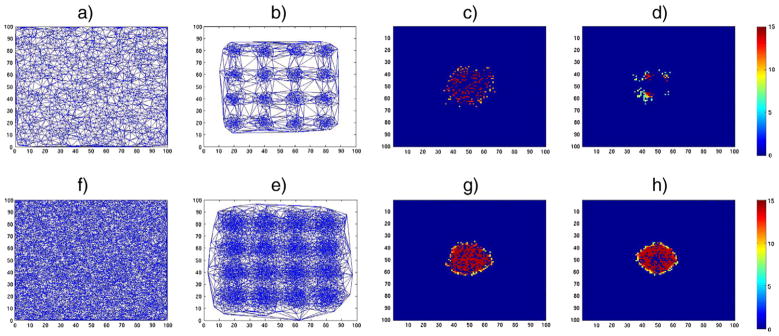
An example showing the effect of uniform vs. non-uniform sampling in different resolutions in our framework. A signal is defined as a circular region with radius 10 centered at (50,50) in a 2D space, and group analysis is performed using our framework on two different groups if images where only one group contains the signal. The resultant p-values are shown in − log scale. a) Delaunay triangulation from 2000 uniformly sampled vertices, b) Delaunay triangulation from 2000 non-uniformly sampled vertices (Gaussian distribution at various grid-points), c) result using mesh a), d) result using mesh b), e) Delaunay triangulation from 10,000 uniformly sampled vertices, f) Delaunay triangulation from 10,000 non-uniformly sampled vertices (Gaussian distribution at various grid-points), g) result using mesh e), h) result using mesh f).