Figure 2.

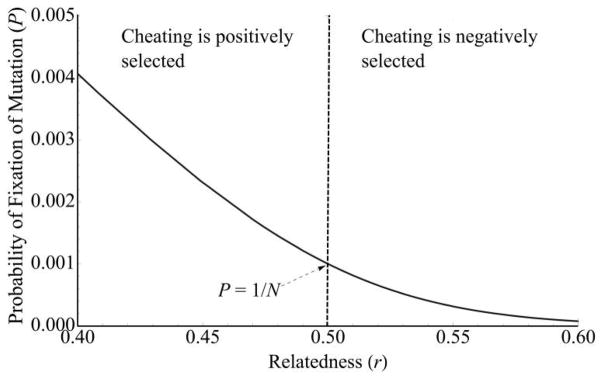
Relatedness can reverse the dynamics of spread of a newly arisen “cheating” mutation. The curve shows the probability of fixation of a newly arisen cheating mutation at the signal locus (under model 1, where signal mutants do not pay the cost of signaling). The dashed vertical line indicates neutrality, that is, the point where the inclusive fitness effect of the cheating mutant equals 0. The probability of fixation at neutrality equals the frequency of the mutant, which is for 1/N a new mutation. The direction of selection depends on relatedness. Cheaters act as deleterious mutants (in which the probability of fixation is less than that for neutral mutations) when relatedness is high but beneficial mutants (in which the probability of fixation is greater than that for neutral mutations) when relatedness is sufficiently high. The curve has a maximum value at r = 0 of P = 2c, corresponding to the fixation probability of a beneficial mutation at a nonsocial locus, where c is the cost of producing the quorum sensing signal. Parameter values are as follows: c = 0.01, b_R = 0.02, N = N_e = 1,000, and ϕ = 1.