Skip to main content
. 2014 Jul 15;107(2):514–526. doi: 10.1016/j.bpj.2014.06.011

Figure 7.

Figure 7

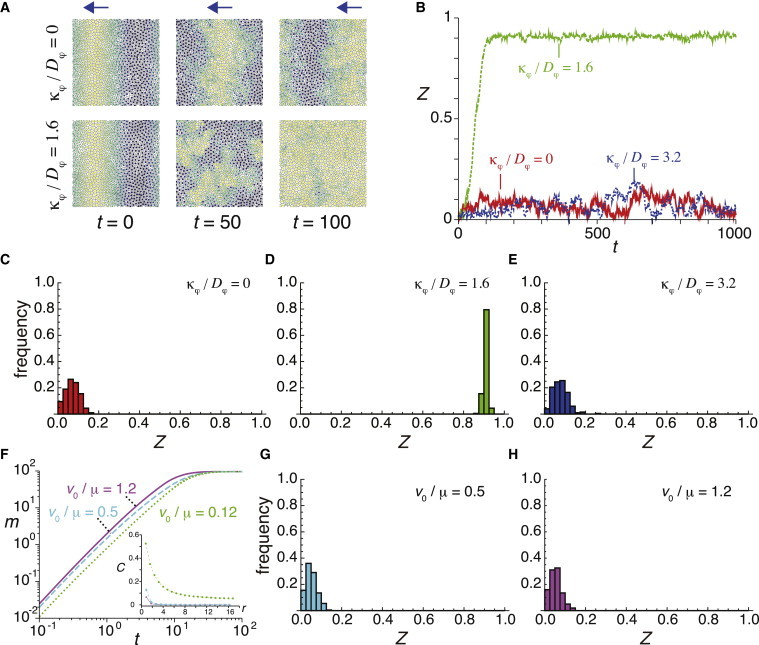
A short-range velocity correlation disturbs spatial phase waves and leads to global synchronization. (A) Kinematic phase wave for κφ/Dφ = 0 (top) and its destabilization for κφ/Dφ = 1.6 (bottom). The blue arrows indicate the direction of motion of the phase wave. The color indicates the intensity determined by (1 + sin θi)/2 as in Fig. 2. (B) Time evolution of the phase order parameter Z(t) for different values of κφ/Dφ, starting from an initial condition with a phase gradient Eq. 12. A single realization for each κφ/Dφ is plotted. (C–E) Histogram of the order parameter Z at t = 1000 for (C) κφ/Dφ = 0, (D) κφ/Dφ = 1.6, and (E) κφ/Dφ = 3.2 when the initial condition of the simulations is a phase gradient Eq. 12. (F) Time evolution of m(t) for different values of v0/μ. Inset: velocity cross correlation C(r) for corresponding v0/μ. (G and H) Histogram of the order parameter Z at t = 1000 for (G) v0/μ = 0.5, and (H) v0/μ = 1.2. In all panels, L = 24, N = 800, v0 = 1.2, Dφ = 0.5, ω = 2.1, and Dθ = 0.1 in Eqs. 1–5. For (A–E) μ = 10. For (F–H) κφ = 0.8. In (C–E, G, and H), the results of 200 different realizations are used for each histogram. To see this figure in color, go online.